黏土中防沉板—桩复合基础地震反应特性研究
2022-03-02关盛杰孔德森王晓敏
关盛杰,孔德森, 2,王晓敏,巩 越
(1. 山东科技大学 土木工程与建筑学院,山东 青岛 266590;2. 山东科技大学 山东省土木工程防灾减灾重点实验室,山东 青岛 266590)
当前我国的海洋油气资源开发正由浅海向深海发展[1],深海的地质条件不同于浅海,在一些工程实践中,作用在基础上的荷载往往超过典型尺寸防沉板的承载极限,为了克服防沉板应用上的局限性,在防沉板下打入桩基础组合成复合基础,旨在不增加防沉板尺寸的前提下,依靠桩基础将荷载传递到深层土体中,提高基础的承载力,目前已经在石油开采项目中进行了工程实践,随后一些学者对其承载力进行了初步研究。
Dimmock等[2]假设仅防沉板承担竖向荷载,防沉板和桩共同抵抗弯矩,提出了简化的下限设计方法,然而这种简化的方法只适用于在设计的可行性验证阶段初步估计复合基础的承载力。Gaudin等[3]通过离心机试验研究了混合基础的承载性能,确定了混合基础的破坏方式。这些研究多是针对工程设计实例的静力学分析验证[4-9],作为水下生产系统的基础,其上部承担着生产设备等主要结构物,一旦发生地震,有可能造成破坏性后果,因此开展防沉板—桩复合基础的动力学分析具有十分重要的意义。Zargar等[10]提出一种海上固定式平台动力反应分析方法,在时域内考虑了土体非线性、桩土界面不连续、土体辐射阻尼引起的能量耗散、结构材料非线性和几何非线性等因素的影响,并得出由于土体的非线性和辐射阻尼,使得平台单元的位移更大,结构单元应力降低。Hesar[11]针对地震荷载下跳线、跨管连接等复杂集群产生的系统效应问题,介绍新的建模和模拟方法。段高松[12]研究了深海条件下输入地震动特性和场地条件对防沉板动力反应的影响,并对比分析了基础埋深、上部荷载及长宽比对基础震陷的影响。
由此可见,防沉板—桩复合基础进入工程应用以来,有关的地震荷载下动力反应分析的研究极少,为了给工程抗震设计提供有益参考和指导,采用Flac3D快速拉格朗日有限差分软件分别建立典型防沉板尺寸与不同桩长组合的复合基础模型,对比分析不同桩长下的复合基础结构体系在地震荷载下的反应特性,对于完善防沉板—桩复合基础的抗震设计理论和优化抗震结构形式具有重要意义。
1 计算模型建立
1.1 模型建立
以南海某深水防沉板工程为例,建立数值计算模型。参考已有的工程设计实例[13-14],确定防沉板模型尺寸为10 m×5 m×0.2 m,角桩增设在防沉板四角,以“销钉”方式连接来限制转动。借鉴海上能源部门常用桩基尺寸参数,本次模拟的桩基直径0.6 m,长度取4 m、6 m、8 m,三种桩长下的复合基础编号分别为HSF-Ⅰ、HSF-Ⅱ、HSF-Ⅲ,并分别定义1~4号桩的顺序,防沉板—桩结构体系如图1所示。
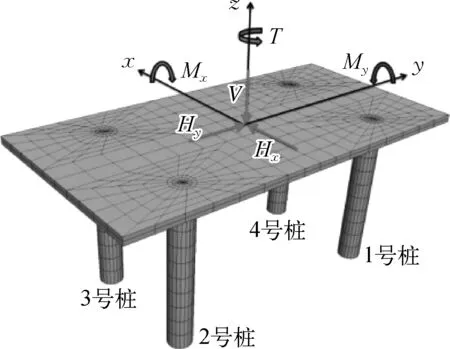
图1 防沉板—桩结构体系平面图Fig. 1 Plan of mudmat-pile structure system
复合基础材料为理想弹性的高强钢材,弹性模量E=206 GPa,泊松比ν=0.3,密度7 850 kg/m3。地震荷载作用下,复合基础与土相互振动激发的应力波传输到边界后会反射,从而影响计算精度,合理选择模型尺寸可以减小边界效应的影响。借鉴曹维科[15]的研究经验,选取土体计算模型长50 m、宽25 m、深20 m。Flac3D的基本原理是通过求解运动方程来解决准静力学和动力学问题,这两类问题都涉及到阻尼问题,只不过对于静力学问题需要设置更多的阻尼来使得模型快速达到收敛状态,对于动力学问题,只要选择合适的阻尼形式和阻尼参数即可描述土体和复合基础在地震荷载下的动力特性,因此土体选择Mohr-Coulomb本构模型。土体弹性模量E=48 MPa,泊松比ν=0.3,体积模量K=E/3(1-2ν)、剪切模量G=E/2(1+ν),土体参数及作用在基础上的设计荷载列于表1,设计荷载作用方向如图1所示。

表1 土体参数及设计荷载
1.2 阻尼的确定
Flac3D提供了三种阻尼形式,其中,瑞丽阻尼动力计算时间步过小,计算负担太重;软件内置的滞后阻尼采用几个连续的函数来表征模量的衰减,阻尼系数获取困难;局部阻尼的原理是通过在震动过程中改变节点质量达到体系的快速收敛,当节点速度改变时即增加质量,当节点速度达到最大值或最小值时减小节点质量,整个过程中损失的能量ΔW与最大瞬时应变能W的比值与频率无关而与临界阻尼比D相关,因此可得如下方程:
αL=πD
(1)
式中:αL为局部阻尼系数,D为临界阻尼比。
由此可见,局部阻尼系数获取方便,不需要设置额外的参数。且对于Mohr-Coulomb材料而言,塑性流动可以耗散大量能量,选取额外的阻尼对于计算结果并不是那么至关重要[16]。因此本模型选择局部阻尼,对于岩土类材料,临界阻尼比D一般取2%~5%,参考前人的计算经验[17],临界阻尼比取5%,局部阻尼为0.157 1。
1.3 边界条件
数值计算模型动力边界选择自由场边界,其原理如图2所示,在模型的边界处分别设置切向和法向阻尼器以吸收边界处的反射波,模拟无限边界模型效果,自由场模型包括四个侧面以及四个角点处的自由场网格,侧面网格与主体网格节点之间是一一对应关系,如图3所示。主体网格的侧向边界通过阻尼器与自由场网格耦合在一起,从而实现了边界条件的模拟,如果地面没有结构物,主体网格和自由场网格一起移动,侧向阻尼器将不会产生作用,当地面存在结构物时,侧向阻尼器将发挥类似于安静边界的效果,吸收结构物震动产生的二次波。自由场网格的不平衡力施加到主体网格的边界上,所施加的力按照下式进行计算:
(2)

图2 自由场网格与主体网格示意Fig. 2 Schematic diagram of free field grid and main grid

图3 自由场边界示意Fig. 3 Free field boundary diagram

1.4 接触面设置
采用“移来移去法” 建立接触面,图4为接触面示意图。Flac3D接触面是由库伦滑动、拉伸强度和剪切黏结来描述的,接触面单元的本构模型如图5所示,在每一个计算时步中,会计算出接触面单元节点和所连接的目标表面的法向变形绝对值和相对剪切速度,根据接触面本构模型,利用这两个值可求出接触面间法向力和剪切力矢量[18]。接触面的法向弹簧刚度kn、剪切弹簧刚度ks、黏聚力c和摩擦角φ的取值参考文献[17-18],各参数列于表2。

图4 接触面示意Fig. 4 Schematic diagram of the interface
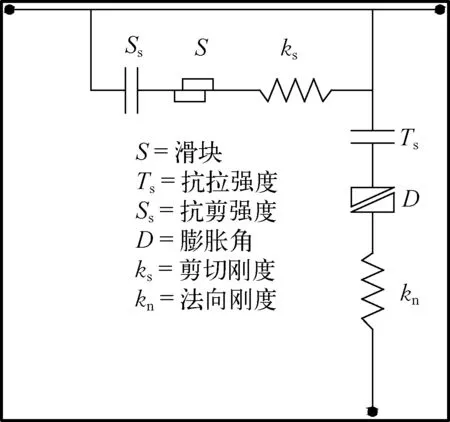
图5 接触面本构模型Fig. 5 Constitutive model of the interface

表2 防沉板和桩基础接触面参数
1.5 地震波的选取与输入
选择EL Centro地震波作为本次模拟的动荷载,加速度时程曲线如图6所示,在0~2.14 s内加速度达到峰值0.35g,5 s之后加速度逐渐减小,较大的加速度主要集中在0~5 s范围内,因此动力计算至5 s结束。地震波中的高频波段对模型网格的最小尺寸有重要影响,过小的网格会直接限制了计算效率,因此采用Flac3D内置的Dynamic Input Wizard功能模块过滤掉地震波的高频部分,同时对计算结果又不会造成显著影响。滤波完成后,对速度时程曲线和位移时程曲线进行基线平衡,避免动力计算结束时模型内部仍有残余的速度与位移。土体模型底部为基岩,弹性模量E=1.28 GPa,泊松比ν=0.29,属于刚性基础,可不设置安静边界条件,直接将加速度施加在模型底面[19],计算深度为20 m。
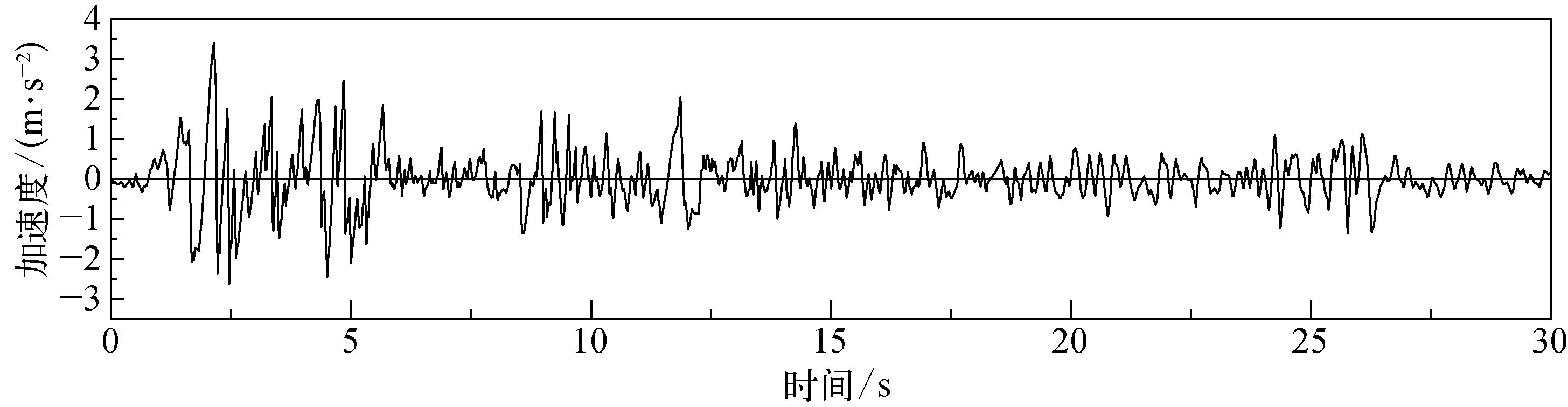
图6 EL Centro地震波加速度时程曲线Fig. 6 Time-history curve of EL Centro wave acceleration
1.6 算例验证
为了验证自由场边界和地震波输入方式的合理性,选取50 m×25 m×20 m土体模型进行计算,模型底部为1 m厚的岩石,上部为土体,土体、基岩力学参数同前。采用线弹性本构模型,四周为自由场边界,在底部施加剪切脉冲波:
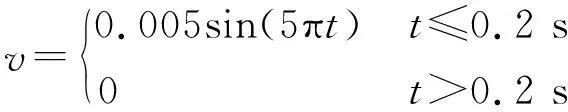
(3)
式中:v为施加的脉冲波速度,t为动力时间。
剪切波在土体中的传播速度按照下式计算,脉冲波由底部传输到顶部所需的时间为0.185 8 s。

式中:Cs为剪切波波速,其余参数意义同前。
算例计算时间为1 s,分别监测模型底部、顶部的速度,其速度时程曲线如图7所示,脉冲波从模型底部向上传播,在0.1 s时底部速度达到峰值0.05 m/s,约经过0.181 3 s传播到模型顶部,在0.293 2 s处顶部速度达到峰值,顶部因是自由界面脉冲波向下反射,从而速度峰值放大了2倍。在0.2 s之后,底部速度为零,顶部约在0.7 s出现第二个峰值,其原因为脉冲波传播到基岩与土体分界面时发生反射,反射的脉冲波向上传播再次到达顶部。由此可见,设置自由场边界并以速度的方式施加地震波是合理的,具有较高精度。
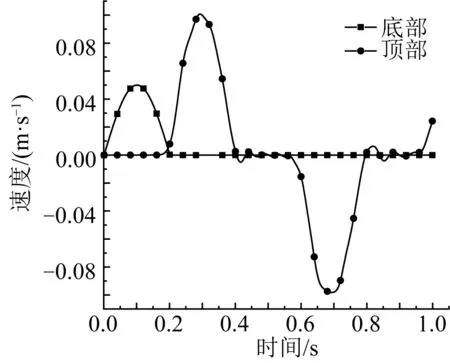
图7 模型底部、顶部的速度时程曲线 Fig. 7 The velocity time history curve at the bottom and top of the model
2 动力反应特性对比分析
2.1 复合基础加速度时程曲线对比分析
图8是三种复合基础位于防沉板中心点处的加速度时程曲线,对比发现,三种复合基础的加速度时程曲线变化规律基本一致,加速度峰值约为输入地震波加速度峰值的4倍,且峰值加速度均为瞬时加速度,说明地震波在向上传播的过程中被放大;瞬时加速度存在的原因为土体底部存在模量较大的岩石[19]。
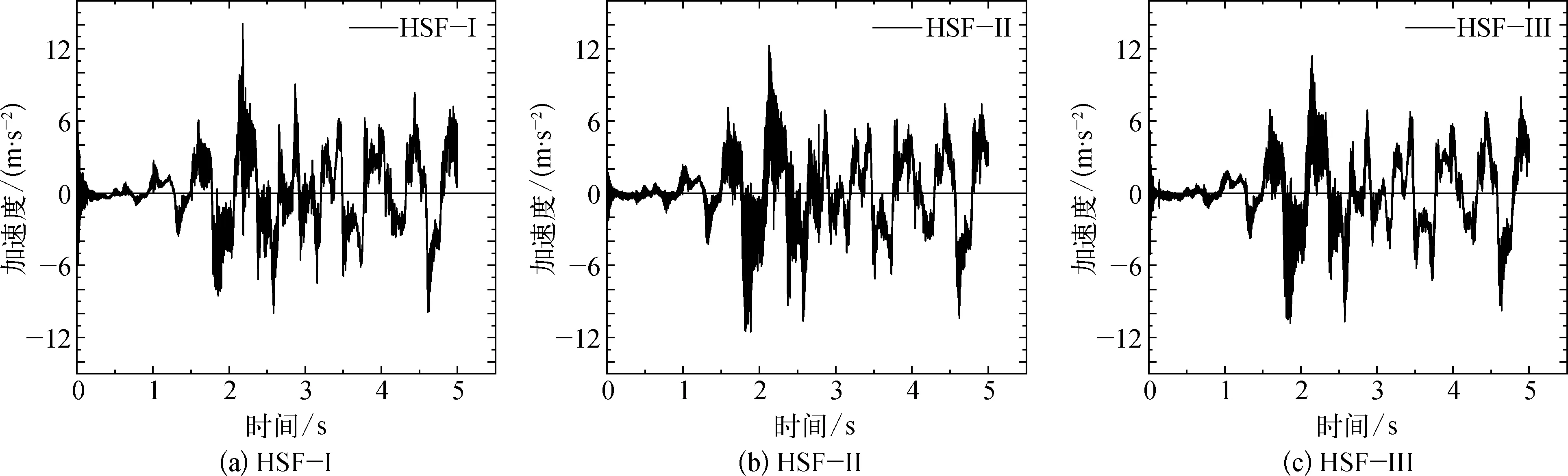
图8 不同桩长下复合基础的加速度时程曲线Fig. 8 Acceleration time-history curve of composite foundation under different pile lengths
与模型底部输入的地震波相比,三种复合基础顶部加速度达到峰值时间有一定延迟,输入地震波在2.14 s处达到峰值,而桩长为4 m、6 m、8 m的复合基础顶部到达峰值加速度的时间分别为2.18 s、2.15 s、2.14 s,桩基础越长,复合基础顶部到达峰值加速的延迟越小,其原因是在土层参数和震源能量相同的情况下,刺入土层的桩越长,震动能量越早的传播到复合基础结构体系中。在黏土场地上,土层对高频地震波具有过滤作用[17, 19],而防沉板几何中心点处的加速度时程曲线高频部分多于输入地震波,原因为多个桩基础之间的震动响应相互影响所致。三种复合基础顶部的加速度放大系数分别为4.129、3.585、3.332,随着桩长的增加,防沉板顶部加速度放大系数呈现减小趋势,但减小的幅度随着桩长增加而降低,说明在地震荷载作用下,增加桩长可以一定程度提高复合基础的抗震性能;针对南海该特定工程,简单的增加桩长对于提高复合基础抗震性能意义不大,应当将桩长控制在6 m以内比较合理。
2.2 复合基础位移时程曲线对比分析
图9是三种复合基础在防沉板几何中心点处的x向绝对位移曲线,三种复合基础的位移响应趋势基本一致,其绝对位移值大小顺序在不同时域呈现不同规律。仔细对比发现,由于土体的滞后性,复合基础的位移响应几乎总是滞后于输入地震波位移。HSF-Ⅰ、HSF-Ⅲ两者的x位移响应一致性较高,在水平移动方向转变处几乎总是产生更多的附加位移,其原因为:复合基础受到三维组合荷载作用,在地震荷载作用下,当桩长为4 m时,桩基础的嵌固作用较弱,复合基础发生了旋转产生了附加的x位移,该现象可从图11复合基础z向位移时程曲线得到验证,HSF-Ⅰ的z位移上下波动,说明复合基础发生了旋转;当桩长为8 m时,桩长的增加不仅使得震动能量快速传播到复合基础(图8所示),而且HSF-Ⅲ高度增加且桩土模量差较大,HSF-Ⅲ基础摇振剧烈。
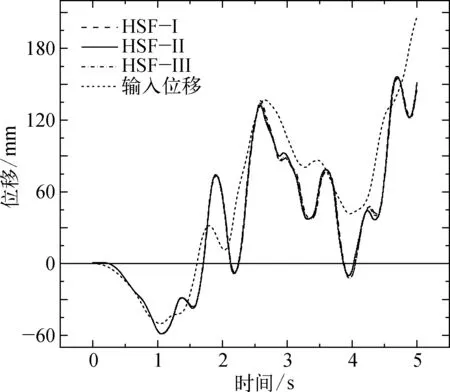
图9 复合基础x向绝对位移时程曲线Fig. 9 x displacement time history curve of composite foundation
为了量化三种复合基础的位移响应,以HSF-Ⅰ的位移为基准,分别将HSF-Ⅱ、HSF-Ⅲ的位移与之作差,如图10所示,Ⅰ-Ⅱ、Ⅰ-Ⅲ分别表示桩长为6 m、8 m时与桩长为4 m时复合基础的x向相对位移差,在0~1.68 s,相对位移差在1 mm以内,在1.68 s之后,随着地震波加速度的增大,相对位移差逐渐增大。对比分析发现,与Ⅰ-Ⅲ曲线相比,Ⅰ-Ⅱ曲线的震动波幅较大,与桩长6 m的复合基础相比,当桩长为8 m时,复合基础在x方向的位移响应值减小约3~4 mm,说明复合基础在x向的位移响应值对桩长敏感,存在最优的桩长可使得复合基础水平摇摆程度最低。
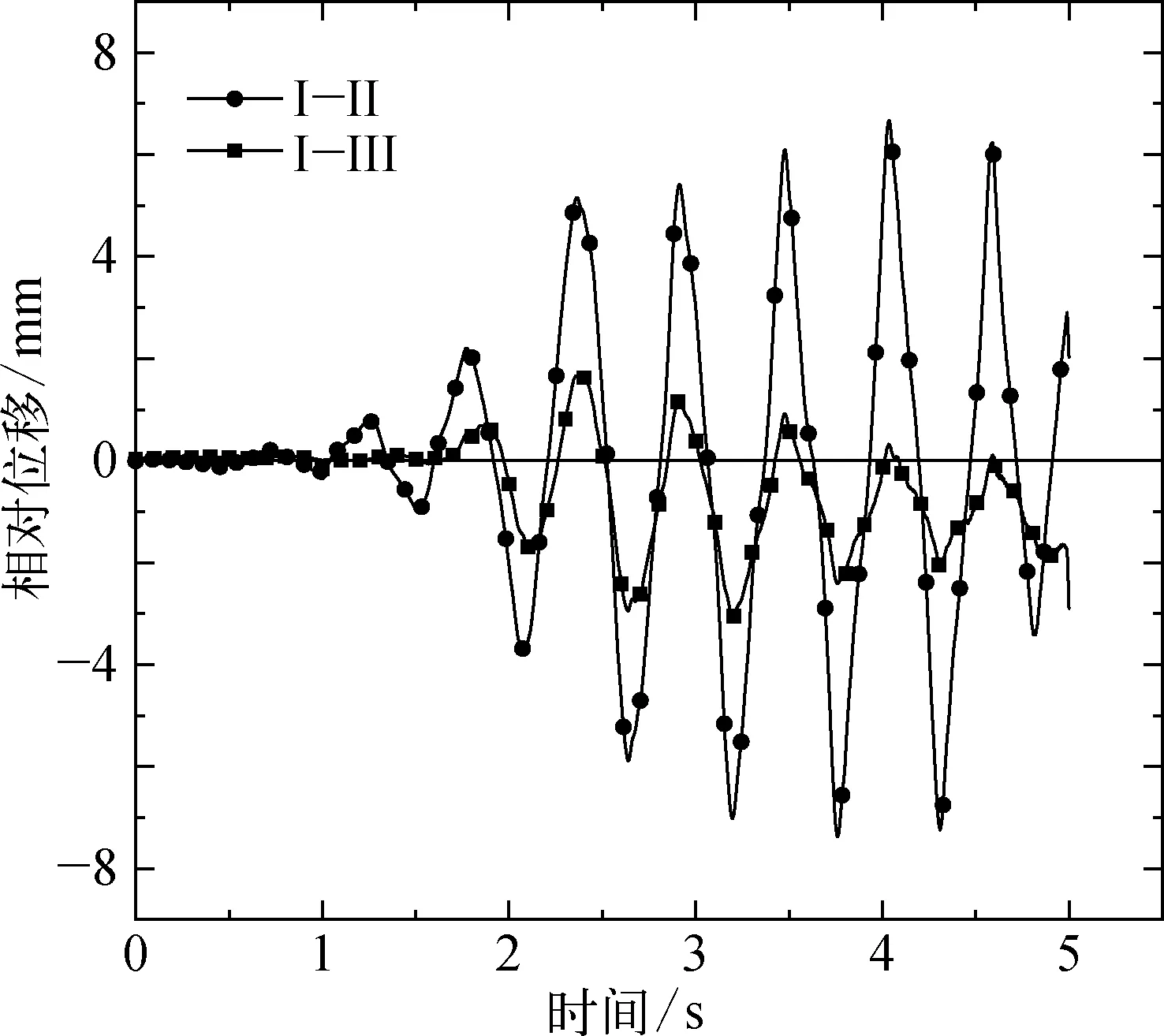
图10 复合基础x向相对位移时程曲线Fig. 10 x displacement time history curve of composite foundation
图11是三种复合基础在防沉板几何中心点处的z方向位移时程曲线,对比分析发现三种复合基础在z方向的位移响应规律基本相同,复合基础在地震荷载作用下产生不可恢复的附加沉降,即震陷[12]。在0~1.6 s,由于地震波加速度较小,土体的地震响应较小,复合基础的z向位移增加缓慢,在1.6~2.14 s,随着地震波加速度增大,复合基础的z向位移响应值快速增加,在2.14 s地震波加速度达到峰值,桩长为6 m、8 m的复合基础的附加沉降约达到11 mm,而桩长为4 m的复合基础竖向位移有较大波动。地震波峰值过后,三种复合基础的z向位移仍有所增加,但增长幅度不大,说明基础震陷在地震波加速度达到峰值时已基本完成,峰值过后不规则荷载所引起的附加沉降只占很小的部分。对比研究发现,HSF-Ⅱ的震陷量同比最小,z向绝对位移与桩长不具单调关系,其原因为:HSF-Ⅰ由于桩长较小而震动剧烈,对下部土体扰动影响较大,从而产生较多沉降;HSF-Ⅲ除了上述摇振现象剧烈外,还由于其桩基较长,桩基础分担了更多的外加荷载,当持力层受到持续扰动时,桩基下沉产生更多的竖向位移。
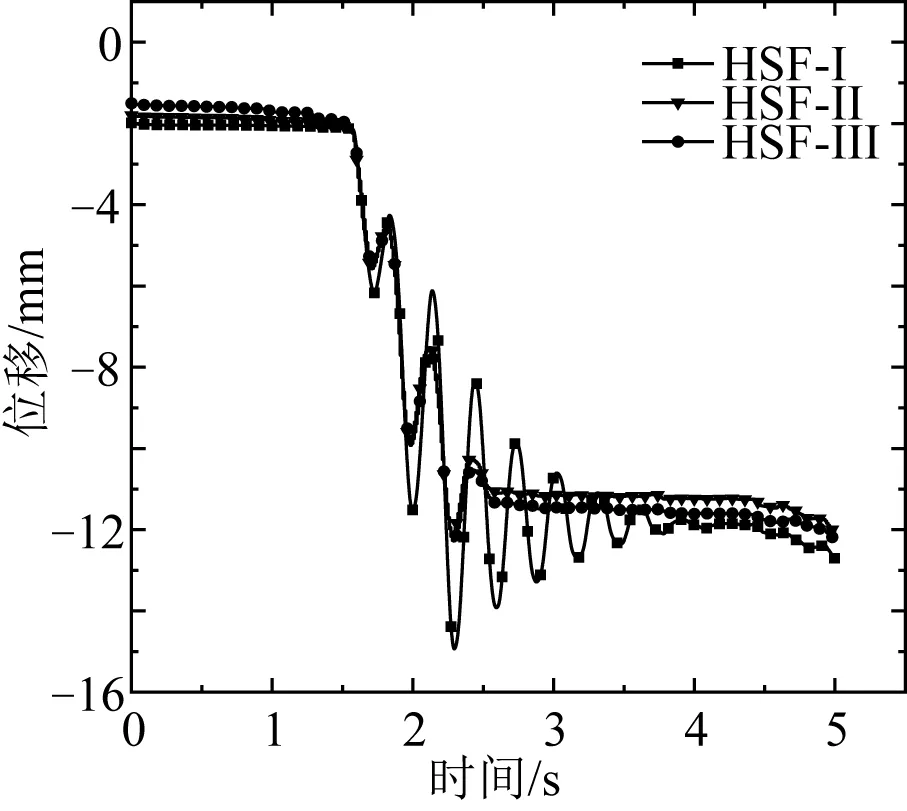
图11 复合基础z向位移时程曲线Fig. 11 Time-history curve of z-direction displacement of composite foundation
2.3 土体动力反应特性分析
为了研究地震荷载作用下复合基础—土体系相互作用规律,分析土体的加速度数值响应差异,分别在近场、远场及不同埋深处设置监测点,监测点方位如图12所示。三种复合基础不同埋深处内场、近场及远场土体的加速度时程曲线如图13所示,加速的峰值列于表3。
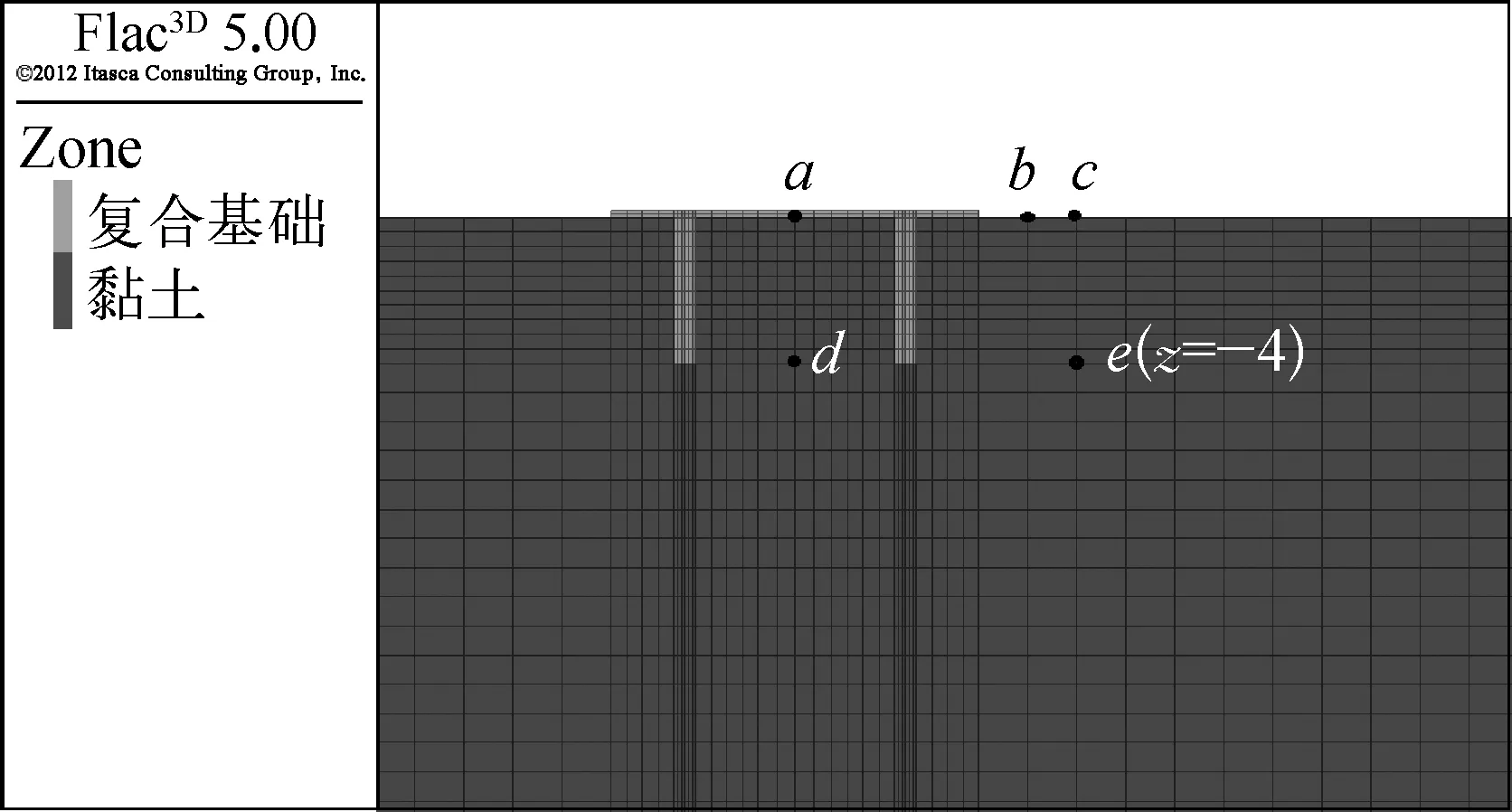
图12 监测点布置Fig. 12 The arrangement of monitoring location
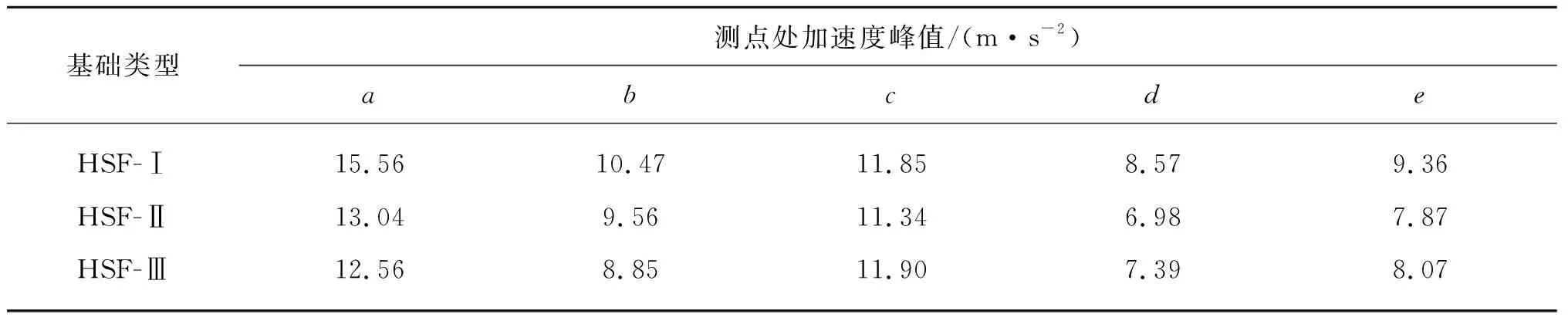
表3 不同位置处土体加速度峰值
图13(a)、(b)、(c)分别为内场、近场及远场地表土体加速度时程曲线,对比图13(d)、(e)埋深4 m处的加速度时程曲线发现,地表处的加速度峰值均大于输入地震波和埋深4 m处土体的加速度峰值,说明地震波在传输过程中被不断放大,这与上述结论一致;受防沉板震动的影响,三种复合基础内场地表土体加速度峰值分别为15.56 m/s2、13.04 m/s2和12.56 m/s2,明显大于近场及远场地表土体;并且防沉板、土体模量相差较大,内场地表土体加速度峰值大于防沉板几何中心处。不同桩长下,远场地表处土体的加速度峰值均大于近场土体,其原因是桩基础的嵌固作用把防沉板顶部震动能量传输到了深层土体,从而距离复合基础较近的近场土体的震动受到抑制,远场土体因为距离较远,能量传播不受限,所以加速度峰值较大。在埋深4 m处,不同桩长复合基础内场土体的加速度峰值分别为8.57 m/s2、6.98 m/s2、7.39 m/s2,对于远场土体处这一数值分别为9.36 m/s2、7.87 m/s2、8.07 m/s2,远场土体的加速度峰值均大于内场土体;并且当桩长为6 m时,复合基础的内场和远场土体加速度峰值均最小,原因考虑为HSF-Ⅱ的对周围土体扰动较小,再次验证上述结论。
2.4 桩身内力对比分析
动力时域内各桩桩顶与防沉板连接处的弯矩变化如图14所示,对比分析发现,不同桩长下桩—板连接处的弯矩变化规律基本一致。在静荷载作用下,位于荷载作用方向前端的1号桩、4号桩桩顶弯矩均大于2号、3号桩;由于桩长增加,荷载作用力臂变长,HSF-Ⅱ和HSF-Ⅲ的桩顶弯矩均大于HSF-Ⅰ。在地震荷载作用下,三种复合基础的桩顶弯矩最大处均为1号桩与防沉板连接处,选取荷载时程为2 s时结果进行分析,三种桩长下复合基础的桩顶弯矩分别为249 kN·m、427 kN·m、525 kN·m,相较于HSF-Ⅰ,HSF-Ⅱ、HSF-Ⅲ的1号桩桩顶弯矩增加了71.48%、110.84%,因此对于长桩复合基础,应该在桩—防沉板连接处增设加固装置。
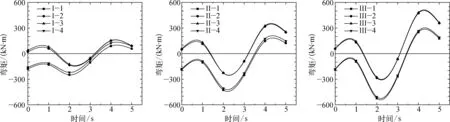
图14 动力时域内桩顶弯矩Fig. 14 Bending moment of pile top in dynamic time domain
3 结 语
基于Flac3D有限差分软件,建立了防沉板—桩复合基础模型,土体选择Mohr-Coulomb本构模型,模型底部输入EL Centro地震波,分析了南海某工程中不同桩长的复合基础在动力时域的地震反应特性,结论如下:
1) 随着桩长的增加,防沉板顶部加速度放大系数呈现减小趋势,减小的幅度随着桩长增加而降低,在该工程背景下,应当将桩长控制在6 m内比较经济合理。
2) 地震荷载作用下,复合基础在x方向的位移响应值对桩长敏感,当桩长为6 m时复合基础水平振动程度最弱;随着地震波加速的增加,复合基础会产生震陷,加速度峰值过后,沉降基本稳定,z向绝对位移与桩长不具单调关系,桩长为6 m时震陷量同比最小。
3) 由于桩基础的嵌固作用,距离复合基础较近的土体加速度响应值小于远场土体。当桩长为6 m时,复合基础对周围土体扰动最小。
4) 地震荷载作用下,桩基础与防沉板连接处弯矩值会增大,此处容易产生破坏。
当土体为饱和状态时,在地震荷载作用下,土体内会产生超孔隙水压力,从而对土体的强度和刚度、防沉板—桩复合基础与土的接触刚度等产生较大影响,因此,后续可考虑饱和黏土的孔隙水压力变化规律,开展防沉板—桩复合基础与土相互作用的流固耦合分析,以研究饱和黏土超孔隙水压力的变化对防沉板—桩复合基础地震反应特性的影响,从而为该区域工程建设提供理论参考。
