弯曲柔性立管举升气液两相流时的流固耦合效应研究

高 岳，朱红钧, 2，王珂楠，颜知音，胡 洁

(1. 西南石油大学 石油与天然气工程学院，四川 成都 610500; 2. 天津大学 水利工程仿真与安全国家重点实验室，天津 300350; 3. 海洋石油工程股份有限公司，天津 300452; 4. 中国石油西南油气田公司天然气净化总厂，重庆 400021)

随着海洋油气混输工艺的发展，气液两相流通常以混输的形式输送至终端平台，因地形起伏或流量变化，管内出现不同流型的气液两相流。管内流体密度、压力等参数沿立管时空变化，导致立管产生振动。同时，立管振动反作用于管内流体，使气液两相流动态演变，这种流固耦合响应会进一步加剧立管的振动，使海洋立管产生疲劳损伤甚至引发油气泄漏，造成巨大的经济损失和严重的环境污染。因此，开展气液两相流与海洋立管的流固耦合特性研究，对海洋立管的疲劳损伤和寿命预测具有重要的意义。

海洋立管流致振动尤其是外流涡激振动一直是海洋油气开采过程中的热点问题，随着输送压力和流速的增大，内流诱导的立管振动问题也逐渐引起了人们的重视。对此，国内外学者在这方面开展了大量的研究。其中，Yin与Griffith[1]最早开展了两相流流致振动试验研究，分析了非定常动量通量对U形管的影响，发现气液两相流的密度差是影响动量变化的主要因素。Hara与Yamashita[2]以空气和水为介质开展了气液两相流诱导管道振动的试验研究，将管道振动的原因归结为气液两相流密度的变化，与Yin和Griffith[1]的研究结果一致。Riverin和Pettigrew[3]研究了U形管在气液两相流作用下的振动响应，得出气液流动引起的共振是产生强烈振动的原因。Ortiz-Vidal等[4]对比分析了泡状流、分散流及段塞流等不同流型的气液两相流诱导的管道振动特性。Wang等[5]通过建立流固耦合模型，分析了严重段塞流诱导水平管—立管系统振动的机理，得出管道振动响应与严重段塞流的周期性有关。Ma和Srinil[6-7]通过建立二维数值模型研究了段塞流诱导的弯曲柔性立管的振动响应，发现立管的多模态振动响应与多频的段塞流动密切相关。Zhu等[8-10]研究了不同流速、气液比的水动力段塞流作用下悬链线型柔性立管的振动响应，分析了柔性立管平面内振动中出现的模态切换现象。李焱等[11]总结了气液两相流引起的海底管道流致振动问题，指出管道疲劳破坏演化过程及规律还有待进一步研究。谢超[12]运用ANSYS软件对比分析了气液两相流激发立管振动的单、双向流固耦合振动结果，得出单向耦合下立管的最大变形量和最大有效应力均大于双向耦合的结果。许超洋[13]试验分析了气液混输管道的振动幅度、管壁稳定性、冲击载荷等响应特性。马晓旭等[14]试验研究了不同流型气液两相流诱导的U形管振动响应特性，分析了气体表观流速和液体表观流速对振动响应的影响。但这些研究大多只关注了气液两相流对管道振动的影响，鲜少分析管道振动对管内流动特性及流型变化的影响。周云龙等[15]试验研究了起伏振动状态下水平管内两相流的流动变化，通过对气液两相流压差波动的分析，发现振动状态下出现了特有的泡状流及沸腾波状流。Jia[16]利用CFD三维数值模拟方法分析了段塞的形成和衰减变化，研究表明长段塞和大流量会增强管道振动，同时振动也会对段塞的形成产生影响。Hibiki和Ishii[17]发现管道的振动会对管内泡状流的流动特性产生影响，但这种影响不足以改变泡状流的流型。曹夏昕[18]、方红宇[19]、栾锋等[20]、张金红[21]等利用振动台研究了摇摆振动对竖直管、水平管内气液两相流动的影响，分析了振动对管内单相流的摩擦压降及气液两相流的流型、流型转变界限、界面含气率以及摩擦压降等参数的影响，发现振动会使管内气液两相流产生附加惯性摩擦力，增大管内的摩擦压降，并且通过对振动状态下流型转变机理的分析，给出了各流型之间的转变准则关系式。

尽管国内外学者或研究了气液两相流动激发的管道振动，或研究了刚性管道的振动对管内气液两相流动特性的影响，但鲜少同时考虑气液两相流激发的振动及振动对管内流体的影响，缺少对双向流固耦合效应的深入分析，然而这种复杂的流固耦合现象在实际海洋工程中普遍存在，尤其是不稳定的气液两相流流经非线性弯曲的柔性立管时，易激发柔性立管产生多阶非线性振动，这种复杂的多模态振动又会影响管内的流体流动，甚至导致管内气液两相流型出现时空动态演变，进一步加剧立管的振动。因此，下文采用高速摄像非介入测试方法，研究了柔性立管与管内气液两相流的流固耦合效应，以期为实际海洋柔性立管的设计、维护及下游设备的设计提供参考。

1 试验方法

1.1 试验装置

如图1所示，试验在气液两相流循环装置中开展，主要包括内流循环和数据采集系统两部分。内流循环系统的装置主要包括：潜水泵、气泵、气体浮子流量计、液体涡轮流量计、针型阀、T型三通、循环管路和蓄水箱。液体和气体分别通过潜水泵和气泵泵送，经流量计计量后在T型三通混合后进入主管路，在2 m长的水平段充分发展后流入立管测试段，最后经管路流回蓄水箱循环使用。其中，测试立管段在振动和固定两种条件下的正视图如图1(b)所示。

图1 试验布置示意Fig. 1 Schematic of experimental setup

试验中模型立管选用透明的硅胶管，其管长为1.440 m，外径10 mm，壁厚1 mm，立管布置的水平跨度l0为1.029 m，两端固定约束，具体参数如表1所列。为便于捕捉柔性立管的振动位移，沿管长方向均匀地标记了35个黑色标记点，标记点宽度为8 mm，相邻两个标记点的中心间距为40 mm。为研究固定立管内的两相流动特征，将柔性立管整体固定于如图1(b)所示的垂直平板上，以限制立管的振动。

表1 立管模型参数

数据采集系统利用非介入高速摄像技术[8-10]同步捕捉振动和流动信息，三个压力传感器分别布置在水平段及立管进、出口处，同步采集管内流动压力信号，其中高速摄像机型号为HXG20，最大像素为2 048×1 088，拍摄频率为100 f/s(frames per second)。高速摄像机的布置位置如图1所示，分别捕捉平面内(xoz平面)和平面外(y方向)的振动位移。拍摄时，同步触发高速摄像和压力传感器以采集立管的振动和管内的流动信息。通过图像后处理得到每个点的振动时程曲线，对100 s时间段的振幅时间序列求均方根，从而得到每个标记点处的均方根振幅，其计算公式如下：

(1)

式中：Ai是i时刻的瞬时振幅；N为样本时间序列数，100 s内高速摄像记录了10 000帧图像，即N=10 000个样本数据。

对于柔性立管的进出口压差，其计算公式如下：

ΔPi=Pin,i-Pout,i

(2)

式中：Pin，i、Pout，i分别为i时刻柔性立管底部入口与顶部出口处的压力。

1.2 试验组次

试验中，固定液体流量通过调节阀门改变气体流量开展了不同流型的气液两相流作用下柔性立管与管内气液两相流的流固耦合响应测试。其中，为捕捉到预期的泡状流、段塞流、搅拌流等不同流型，参考了1983年Barnea等[22]在8.15 mm管径直管中开展气液两相流型试验研究时选用的流速范围，取液体表观流速范围为0.01～1.02 m/s、气体表观流速范围为0.02～6.63 m/s。

1.3 衰减试验测试

试验测试前，首先进行了衰减测试。通过对振动衰减曲线进行快速傅里叶变换(FFT)，得到柔性立管的前两阶自振频率，其中平面内x和z方向的自振频率相同，充水管的一阶自振频率皆为2.25 Hz，二阶自振频率为3.74 Hz，具体的自振频率见表1。

2 结果与分析

2.1 固定立管内的流型分区

以往对管内流型的研究主要针对垂直、水平以及固定夹角的倾斜管，随着管道倾角的变化，管内的流型会随之变化，而试验中柔性立管的曲率是随立管高度不断变化的，如图2所示，试验观察到的流型主要有：泡状流(bubbly flow)、泡状—段塞流(bubbly-slug)、段塞流(slug flow)、段塞—搅拌流(slug-churn)和搅拌流(churn)。所有试验组次的流型分区如图3所示，由于管材、管径及悬链线型立管的曲率不断变化等原因，这里的流型分区与垂直管[22]及45°倾斜管[23]内的流型分区存在一定的差异，在较小的气体表观流速时出现了垂直管和45°倾斜管中没有发现的气泡流。

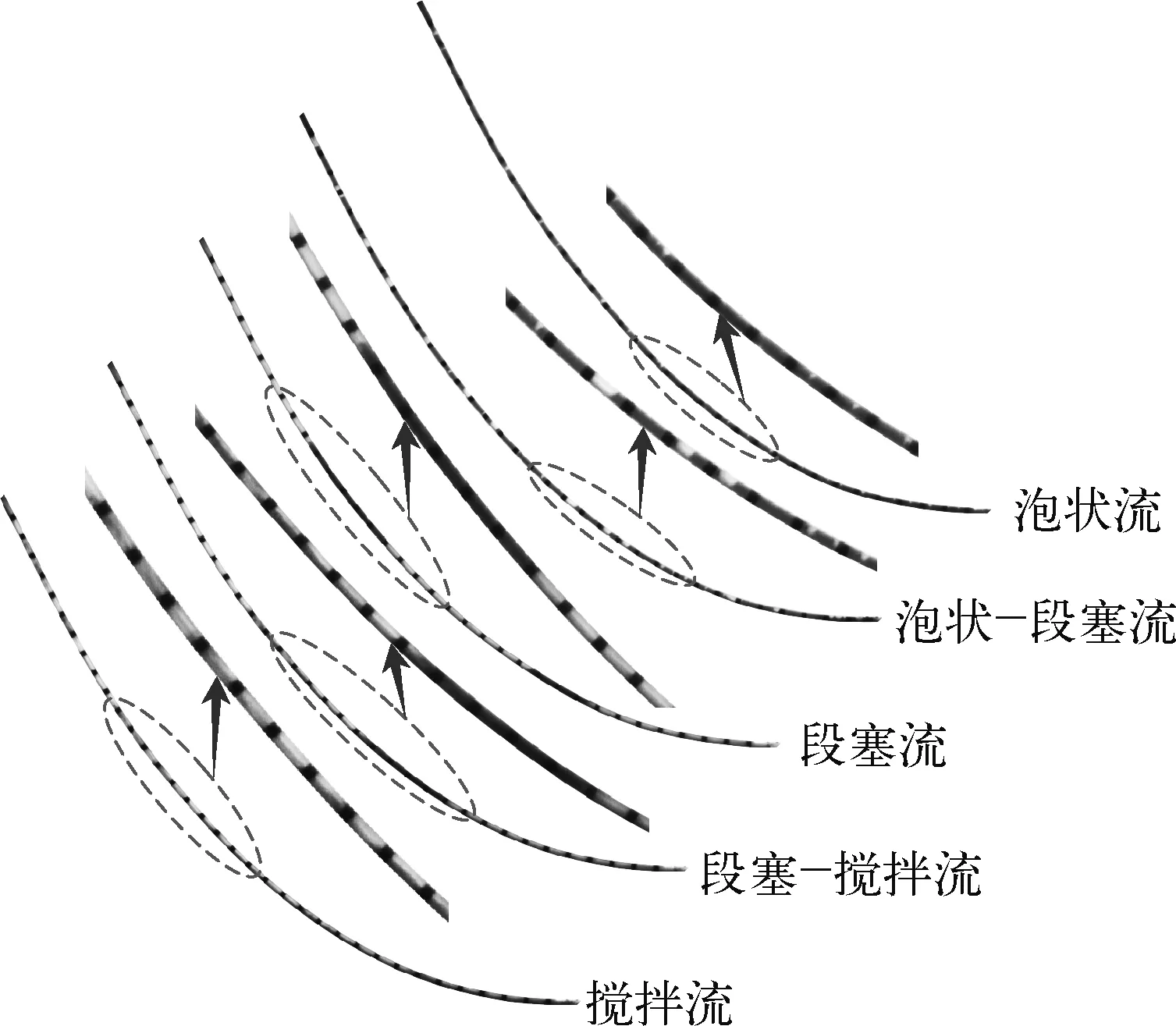
图2 固定立管内出现的不同流型Fig. 2 Flow patterns in the fixed flexible riser

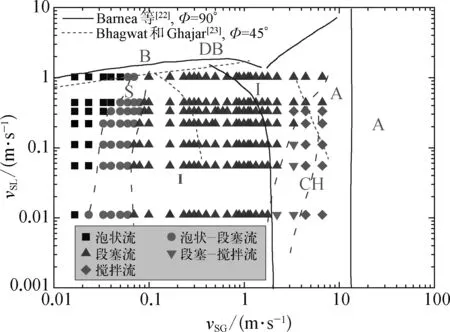
图3 固定立管中的流型分区Fig. 3 Flow pattern map in the fixed flexible riser

多尺度熵在流型识别中应用广泛[15, 24-25]，不同流型的多尺度熵特征可以反映其流动特性，对立管内出现的几种流型的压差信号进行多尺度熵分析，计算过程中容限r取序列标准差的0.15倍[26]，维数m取2，最大粗粒化尺度为15，压差数据长度为9 000点。图4展示了液体表观流速为0.11 m/s时不同流型的气液两相流作用下立管进出口压差波动信号的多尺度熵计算结果。

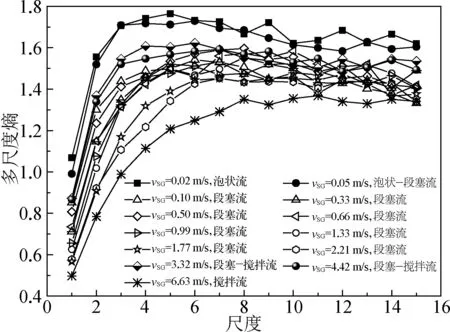
图4 不同流型进出口压差的多尺度熵Fig. 4 Multi-scale entropy of pressure difference under different flow regimes

由图4可知，总体上熵值的大小排序为：泡状流>泡状—段塞流>段塞—搅拌流>段塞流>搅拌流，泡状流的压差信号最复杂，搅拌流的压差信号复杂度最低。不同流型的压差在前4个尺度上的熵值变化趋势相似，随着尺度地增大熵值逐渐增大，泡状流的增长速率较快，其次是泡状—段塞流、段塞—搅拌流、段塞流、搅拌流。第5个尺度之后，随着尺度的增大，熵值变化开始出现差异，表现出起伏变化的趋势。由于泡状流中气泡很小，在随液体沿立管向上运动时不规律，气泡在液相中的分布具有随机性、离散性，其多尺度熵最大，复杂度最高。泡状—段塞流具有泡状流的流动特性，且气泡在流动过程中出现合并等现象，因此多尺度熵较大。对于段塞流，其表现为气液交替流动，周期性明显，因此流动相对规律，多尺度熵较小。随着气体表观流速的增大，两相流动受到强烈的扰动，尤其是液塞尾部的溃散，使液体出现上下振荡的现象，在管壁上形成强烈的冲刷，管内流体流动变得复杂、随机，使得段塞—搅拌流的多尺度熵较大，但小于泡状流和泡状—段塞流。搅拌流流动时，尽管气液两相掺混在一起，由于液体含量减少，流体重量的影响减小，使液体上下振荡的现象减少，流动行为趋于稳定，因此搅拌流的多尺度熵较小。

2.2 流固耦合响应

2.2.1 不同流型气液两相流作用下的立管振动特性

为研究不同流型气液两相流诱导的立管振动响应，选取液体表观流速为0.11 m/s，气体表观流速从0.02 m/s 增至6.63 m/s时的13个组次进行流固耦合分析。图5比较了不同流型的气液两相流作用下柔性立管在平面内x、z两个方向及平面外y方向的均方根振幅分布。其中，s为沿管轴方向某点距离立管底部的轴向长度，s/l为沿管轴方向某点距离立管底部的无量纲轴向长度，Ax，RMS/D与Az，RMS/D分别为立管在x和z方向的无量纲均方根振幅。在本试验的气液流速范围内，与平面内x、z两个方向上的振动相比，平面外y方向的振动很小(见图5(c))，可以忽略，故下文重点分析平面内的振动响应。由图5可知，不同流型的气液两相流作用下柔性立管的振动强度不同，但主要为一阶模态振动，根据气液两相流诱导的立管振动强度从大到小可将流型排序为：段塞—搅拌流、段塞流、搅拌流、泡状—段塞流及泡状流。

图5 不同流型气液两相流作用下的立管均方根振幅分布Fig. 5 Spanwise evolution of root-mean-squared amplitudes under different gas-liquid flow regimes

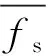
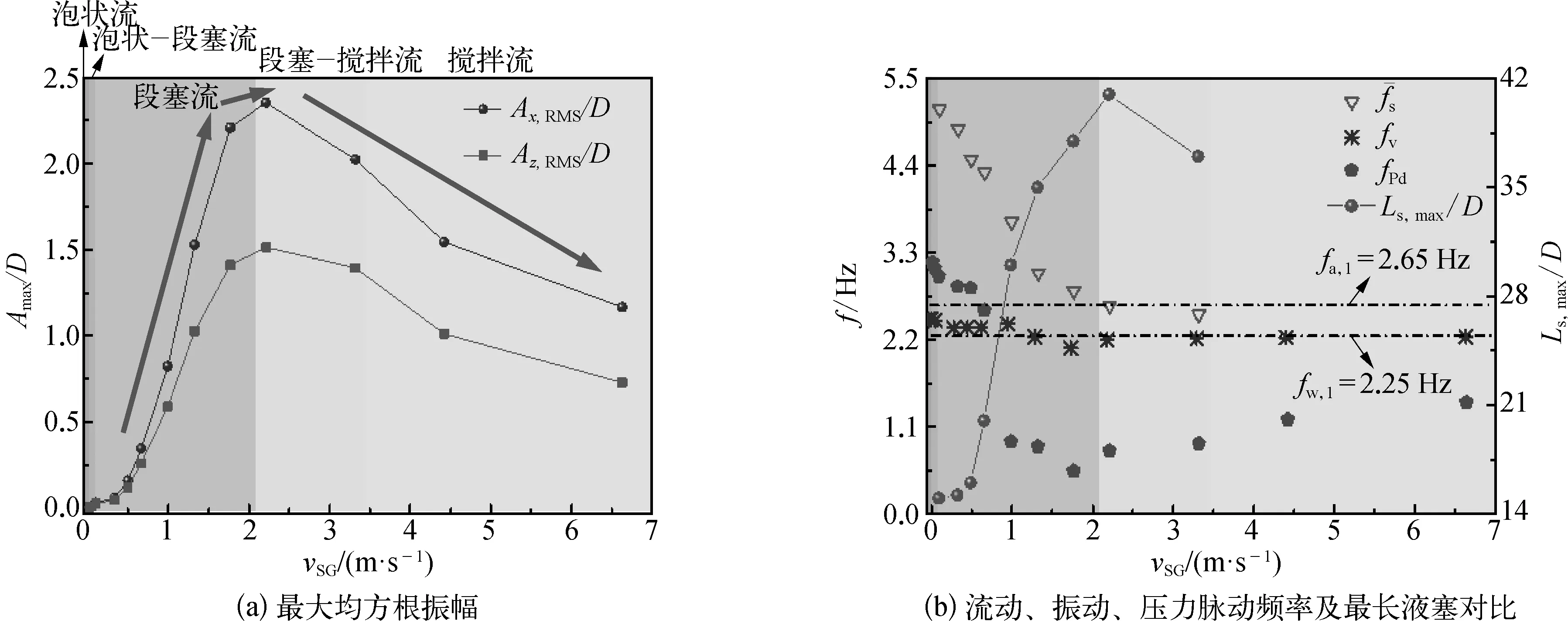
图6 不同流型气液两相流作用下立管的最大振幅及管内流动变化Fig. 6 The maximum root-mean-squared amplitudes and flow variation in the riser under different gas-liquid flow regimes

2.2.2 柔性立管振动对管内流动的影响

1) 柔性立管振动对泡状流和泡状—段塞流的影响

立管振动会影响管内的流动，图7对比了柔性立管在固定和振动情况下管内泡状流和泡状—段塞流的变化。可见，两种情况下，柔性立管内的泡状流、泡状—段塞流几乎没有变化。如图8所示，微弱的振动对压差脉动曲线及压差多尺度熵的影响很小，这主要是因为两种流型的气液两相流作用下柔性立管的振动很弱，不足以对管内的气液两相流动产生影响。

图7 固定和振动情况下管内泡状流、泡状—段塞流流型的对比Fig. 7 Comparison of bubbly flow and bubbly-slug flow in fixed and oscillation risers

图8 固定和振动情况下泡状流、泡状—段塞流压差时程曲线及多尺度熵Fig. 8 Multi-scale entropy of pressure difference for bubbly flow and bubbly-slug flow in fixed riser and oscillation riser respectively

2) 柔性立管振动对段塞流的影响

图9展示了柔性立管在vSL=0.11 m/s、vSG=1.77 m/s工况下，相同长度的液塞通过固定和振动立管时长度的变化。如图9(a)所示，固定立管中，液塞进入立管时长度为8D，在向上运移的过程中，由于液塞前端吸收管壁上的液膜，长度增大至12.0D，液塞增长率为50%。图9(b)中同样长度的液塞进入振动的柔性立管时，随着液塞向上运移，其长度最终稳定在8.1D，增长率仅为1.25%，变化很小。剧烈的振动会使管内的液膜分散，影响液塞前端对液膜的吸收，同时振动使液塞尾部不稳定性增强，促使液塞尾部的液体脱落，从而使液塞长度增加减小。

图9 固定立管和振动立管中液塞长度的变化Fig. 9 The length variation of liquid slug in fixed riser and oscillation riser respectively

图10(a)对比了相同工况下平均液塞长度在固定和振动立管中的变化。由上述振动对管内液塞长度的影响可知，振动使管内液塞长度减小，如图10(a)所示，振动立管和固定立管中的平均液塞长度差值随气体表观流速的增大而增大，这是由于段塞流作用下，气体表观流速越大，柔性立管振动越剧烈，对管内的液塞长度影响越大。

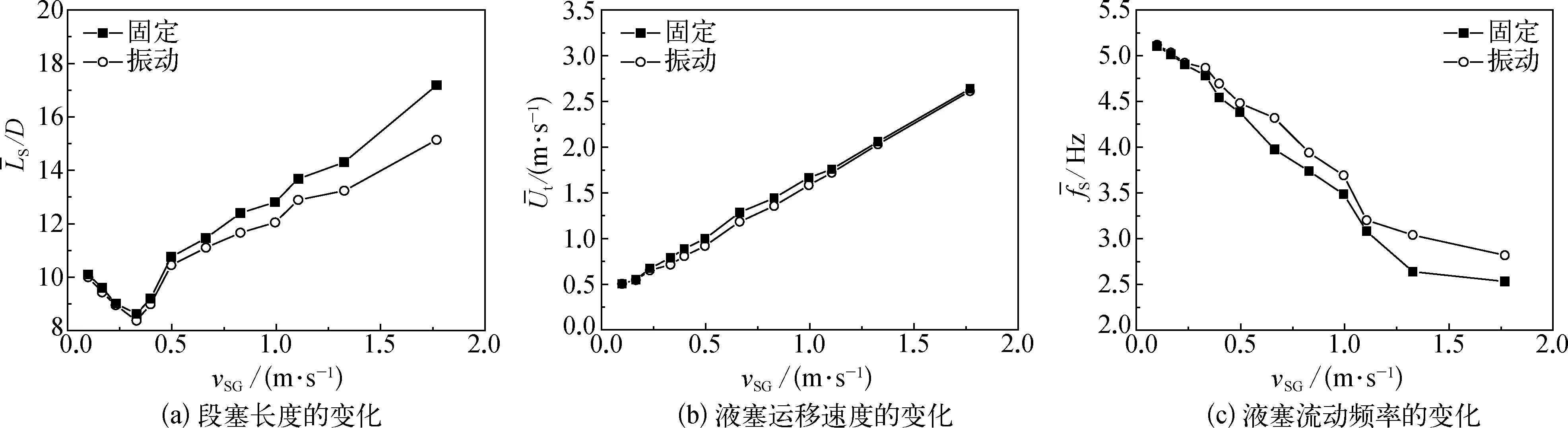
图10 振动对管内段塞流流动的影响Fig. 10 The effect of oscillation on the flow characteristics of slug flow in flexible riser

图10(b)为不同气体表观流速的段塞流作用时柔性立管在固定和振动两种情况下段塞运移速度的对比。可见，振动立管内的段塞运移速度小于固定立管中的段塞运移速度，但差值较小，尤其是在气体表观流速较小时，说明柔性立管的振动对段塞运移速度的影响较小。

与固定立管中的流动频率比较，振动立管中的液塞流动频率增大，这与振动立管中的液塞长度比液塞运移速度减小更明显有关。如图10(c)所示，0.10 m/s≤vSG<0.33 m/s时，柔性立管的振动较小，液塞长度和运移速度变化不明显，导致平均液塞流动频率几乎没有变化。0.33 m/s≤vSG≤1.77 m/s时，气体表观流速越大，平均段塞流动频率增大越明显，这与液塞长度和运移速度的变化有关。

在流型变化方面，0.10 m/s≤vSG≤1.33 m/s时，固定立管和振动立管中的流型均为段塞流，仅在流动参数上发生了变化。如图11(a)所示，vSL=0.11 m/s、vSG=0.99 m/s时，柔性立管内的流型均为段塞流，而vSL=0.11 m/s、vSG=2.21 m/s时，固定立管中的流型为段塞流，振动立管中流型变为段塞—搅拌流，这与此时立管振动较强，对管内的段塞产生强烈的冲击，加速了短液塞的溃散有关。图12展示了vSL=0.11 m/s时vSG=0.99 m/s和vSG=2.21 m/s两种工况下管内气液两相流动压差的变化，从压差波动上可以看出，振动使压差时程曲线的微小脉动增加，且压差均值减小，这与立管振动使管内液塞长度和流动速度减小有关。通过比较压差多尺度熵的变化，发现vSG=0.99 m/s时前5个尺度的熵值变化不大，第5个尺度后，振动立管内的压差多尺度熵大于固定立管中的压差多尺度熵，说明虽然管内的流型未发生变化，但振动增加了管内流动的复杂性。vSG=2.21 m/s时，振动情况下的压差多尺度熵大于固定情况的多尺度熵，这与管内流型由段塞流转变为段塞—搅拌流有关。

图11 振动对管内段塞流流型的影响Fig. 11 The influence of vibration on the slug flow in flexible riser

图12 固定和振动情况下段塞流压差时程曲线及多尺度熵Fig. 12 Multi-scale entropy and time histories of pressure difference of slug flow in fixed riser and oscillation riser respectively

3) 柔性立管振动对段塞—搅拌流及搅拌流的影响

图13(a)对比了vSL=0.11 m/s、vSG=4.42 m/s时，柔性立管在固定和振动两种情况下管内的流型变化。可见，在立管振动的情况下，管内的流型由固定立管中的段塞—搅拌流变为搅拌流，这主要是由于段塞—搅拌流作用时，柔性立管的剧烈振动加速了液塞尾部的脱落，使液塞溃散，形成搅拌流。如图14(a)所示，与固定立管相比，振动时此工况对应的压差多尺度熵减小，气液掺混且气体流量增大，导致管内流体受重力影响减小是熵值减小的原因。图13(b)对比了vSL=0.11 m/s、vSG=6.63 m/s时，柔性立管在固定和振动两种情况下管内搅拌流的流动变化。结果表明搅拌流在柔性立管固定和振动时流型并没有改变，图14(b)显示的对应压差时程曲线及多尺度熵也没有明显的变化，这与搅拌流气液混合分布的特性有关。

图13 振动对管内流型的影响Fig. 13 The influence of vibration on the gas-liquid two-phase flow in the riser

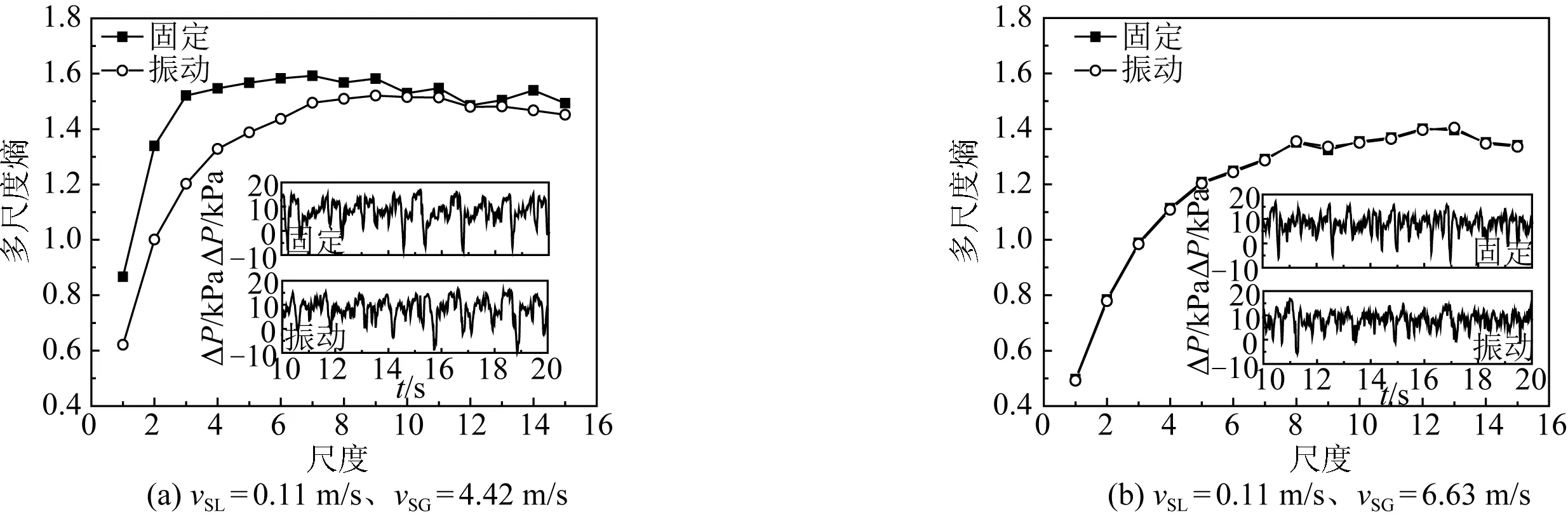
图14 固定和振动情况下段塞—搅拌流、搅拌流压差时程曲线及多尺度熵Fig. 14 Multi-scale entropy and time histories of pressure difference of slug-churn flow and churn flow in fixed riser and oscillation riser respectively

2.2.3 柔性立管的振动对管内流型分区的影响

为分析柔性立管的振动对管内流型产生的影响，将振动柔性立管内的流型进行分区并绘制于图15。

图15 振动立管中的流型分区Fig. 15 Flow regime map in the oscillation flexible riser

其中，虚线代表固定立管中的流型分区界限。与固定的柔性立管内出现的流型对比，立管振动时管内未出现新的流型，但振动使流型分区界限出现偏移。流速较小时，由于立管振动较弱，未对泡状流和泡状—段塞流流型产生影响，对应的流型分区界限没有发生偏移。段塞流作用时，仅在段塞流与段塞—搅拌流交界处出现了流型转变，使段塞流与段塞—搅拌流的分界限向气体表观流速较小的方向偏移。在段塞—搅拌流与搅拌流的交界处固定立管中的段塞—搅拌流则在立管振动作用下转变为搅拌流，如前面所述的vSL=0.11 m/s、vSG=4.42 m/s的组次。

3 结 语

利用高速摄像非介入测试技术，对管内气液两相流与柔性立管流固耦合响应进行了试验研究，结果表明：随着气液流量的变化，柔性立管中出现了泡状流、泡状—段塞流、段塞流、段塞—搅拌流和搅拌流五种流型。对不同流型气液两相流压差的多尺度熵进行分析，发现泡状流的流动最复杂，搅拌流的流动相对稳定。不同流型的气液两相流激发的立管振动响应不同，在段塞—搅拌流作用时立管的振动响应最剧烈，泡状流作用下柔性立管的振动较弱。泡状流、0.10 m/s

本试验采用的是小尺寸的概化模型，旨在分析柔性立管举升气液两相流时的流固耦合效应。下一步将综合考虑管内气液两相流的流动相似和立管振动的结构相似，开展有比尺的模型管道振动测试，以更好地指导生产实际。