基于主动阻尼技术的薄壁件铣削振动控制研究*
2022-02-28何立东杨建江
王 健,何立东,杨建江
(北京化工大学 机电工程学院,北京 100029)
0 引 言
对于现代火箭、飞机等飞行器来说,降低自身的质量,意味着提高推动比、节省燃料。为降低自身质量,其材料一般多采用低密度铝合金,在结构上大面积使用薄壁工件[1]。
航天领域中的薄壁工件尺寸一般比较大且形状复杂,通常要对其进行局部厚度的减薄加工,从而降低重量、提高承载能力[2]。在铣削薄壁工件减重网格的过程中,随着工件的减薄,工件网格处的刚性降低,在切削过程中极易产生切削振动,导致网格处工件精度不高,甚至发生损坏[3]。
目前,在铣削减振方面应用的主要方法有调整铣削参数、优化刀具结构、加强系统刚度、提高系统阻尼等。
宁文波等人[4]通过建立大长径比插铣刀的结构模型,使用有限元分析的方法,研究了刀具的动力学响应和振动特性。SMITH S等人[5]提出了充分利用零件整体刚性的切削加工方案,有效地控制了零件的加工变形,并且提高了工件的加工精度。HARANATH S等人[6]提出了在刀具表面添加粘附阻尼材料的方法来提高系统阻尼,并且分析了阻尼材料不同的覆盖方式对刀具动力学特性的影响。
这几类方法对铣削振动控制有一定效果,但是在这几类方法下,机床、刀具的性能一般难以充分发挥,且灵活性差,影响加工效率[7]。
振动的主动控制是指被控系统发生振动时,控制系统根据传感器测得的振动信号进行信号的分析计算后,驱动作动器对被控系统施加一定影响,从而达到振动控制的目的[8]。这种振动控制策略可以很好地应对被控系统的时变性导致的振动,具有自适应性强、作用频带宽等特点。
笔者将主动阻尼装置(ADD)应用到铣削薄壁件中,利用ADD对薄壁件施加主动控制力,实现薄壁件在铣削减振网格过程中的振动抑制;对比铣刀在不同转速下铣削薄壁件时ADD的振动抑制效果,以及不同网格厚度的薄壁件在使用ADD后的振动抑制效果。
1 主动阻尼装置及控制原理
1.1 ADD组成结构
ADD由ADD控制箱以及ADD作动器两部分组成,ADD控制箱控制ADD作动器进行工作,其实物如图1所示。

图1 ADD组成图
ADD控制原理图[9]94如图2所示。

图2 ADD控制原理图
ADD控制原理为传感器采集被控系统的加速度信号,控制单元对采集到的加速度信号进行处理后发出控制信号,控制信号由功率放大器放大后驱动作动器输出力对被控系统产生影响[10]。
ADD惯性作动器的结构[11]18如图3所示。
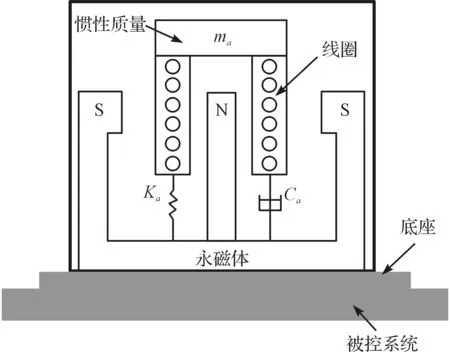
图3 ADD作动器结构
线圈与惯性质量组为一个整体,通过弹簧及阻尼元件与底座连接。线圈通入交流电后产生交变磁场,与永磁铁产生的恒定磁场相互作用产生安培力,惯性质量在电磁力的作用下产生振动,对底座产生反作用力从而影响被控系统。
1.2 ADD作动器动力学模型
ADD作动器的力学模型可以简化为安培力作用下的单自由度受迫振动问题。
ADD作动器力学模型[12]如图4所示。
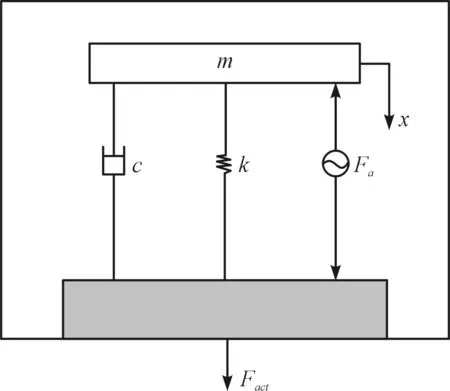
图4 ADD作动器力学模型
作动器的力学模型的振动微分方程为
(1)
式中:m—惯性质量块的质量;x—质量块的位移;c—系统阻尼;k—系统刚度;Fa—惯性质量块受到的安培力。
系统输出的作动力Fact为:
(2)
所以,惯性质量块受到的安培力Fa与系统输出力Fact之间的传递函数为:
(3)
惯性质量块受到的安培力Fa又可以表示为:
Fa=ga·Vin
(4)
式中:ga—作动器输出力常数;Vin—控制电压。
因此,ADD作动器为系统输出的作动力Fa与控制电压Vin之间的传递函数为:
(5)
式中:ωa—作动器固有频率;ζa—阻尼比。
作动器输出力常数ga、固有频率ωa和阻尼比ζa与作动器内部磁场分布情况、线圈绕组、惯性质量大小、阻尼元件及弹簧刚度有关[13,14]。
1.3 直接速度反馈控制原理
直接速度反馈控制原理是将被控系统的振动速度作为反馈控制量。
ADD控制箱给ADD作动器的控制电压为:
(6)
式中:gv—反馈增益系数;x—被控系统测点处的振动位移。
若作动器在线性范围内工作,作动器输出给薄壁工件的作动力可表示为:
(7)
薄壁工件在外部激励下的运动微分方程为:
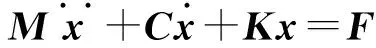
(8)
式中:M—薄壁工件的质量矩阵;C—薄壁工件的阻尼矩阵;K—薄壁工件的刚度矩阵;F—薄壁工件受到的外部激振力矩阵。
在直接速度反馈控制下,ADD作动器向被控系统施加作动力,系统的运动微分方程为:
(9)
可以发现,在直接速度反馈控制原理下,ADD作动器相当于对薄壁工件施加了阻尼力[9]95,因此,采用作动器可以起到控制振动的作用。
笔者所用ADD作动器中,传感器与作动器安装在同一位置,构成传感器到作动器的最小相位系统。可以证明,这种布局方式具有较大稳定裕度[9]95。
笔者设计的ADD作动器具体参数如表1所示。

表1 ADD作动器设计参数
根据表1中参数,笔者对ADD作动器进行了输出力仿真测试分析,得到的作动器的幅频特性仿真曲线[11]20如图5所示。
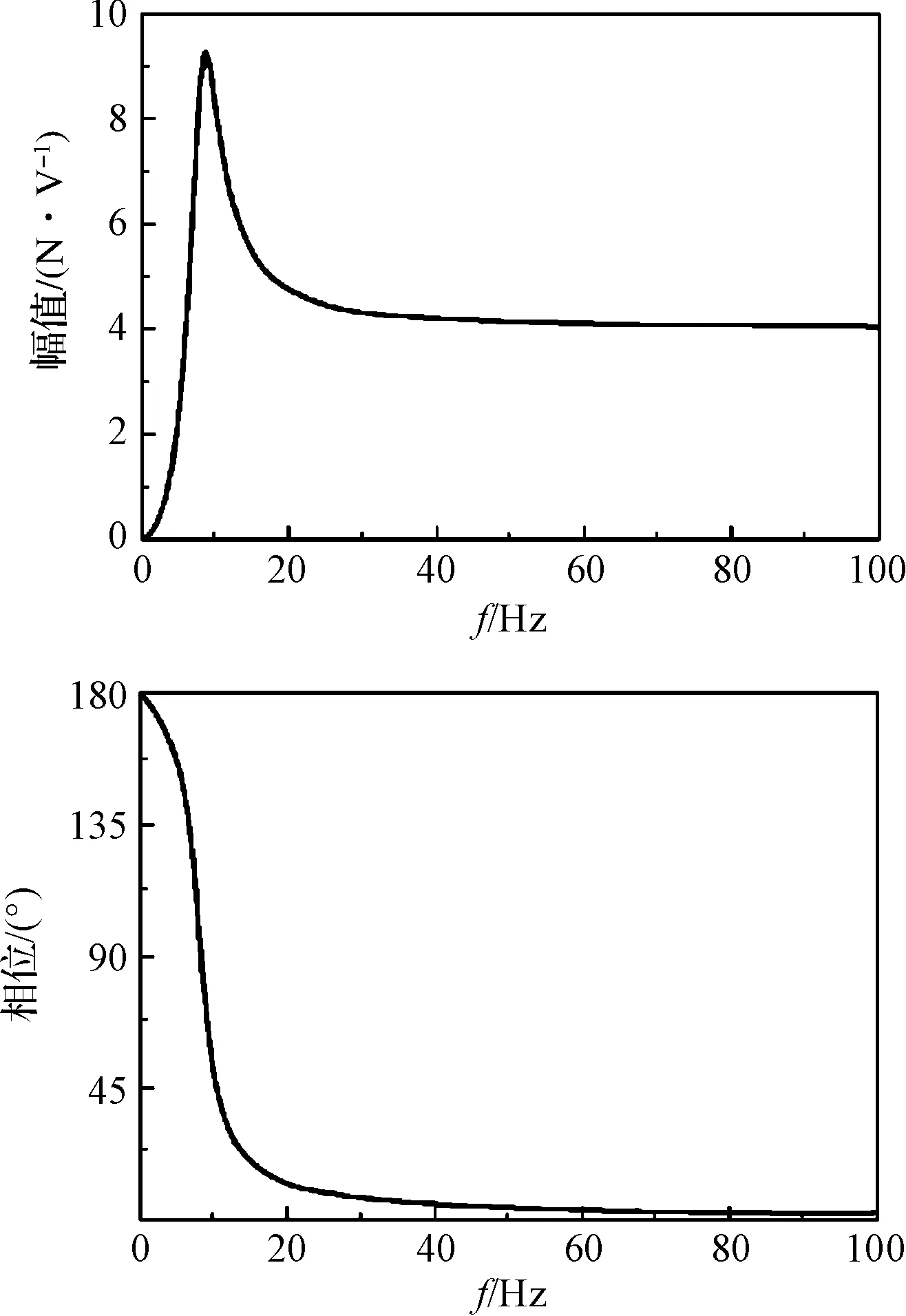
图5 作动器的幅频特性仿真曲线
从图5中可以发现,ADD作动器的输出力大小在一定频率范围内仅与控制电压有关,在这段频率范围内,ADD作动器可以稳定地根据控制信号输出作动力,因此ADD可以控制的振动频带较宽。
2 薄壁件模态振型分析
2.1 模型与计算方法
铣削时,为确定ADD作动器的安装位置,需要对薄壁件进行模态分析。
根据项目实际情况,笔者选择带网格薄壁工件的尺寸为1 260 mm×1 050 mm,整体厚度20 mm,筋肋宽度10 mm,网格大小为200 mm×200 mm,网格剩余厚度2 mm,模型如图6所示。
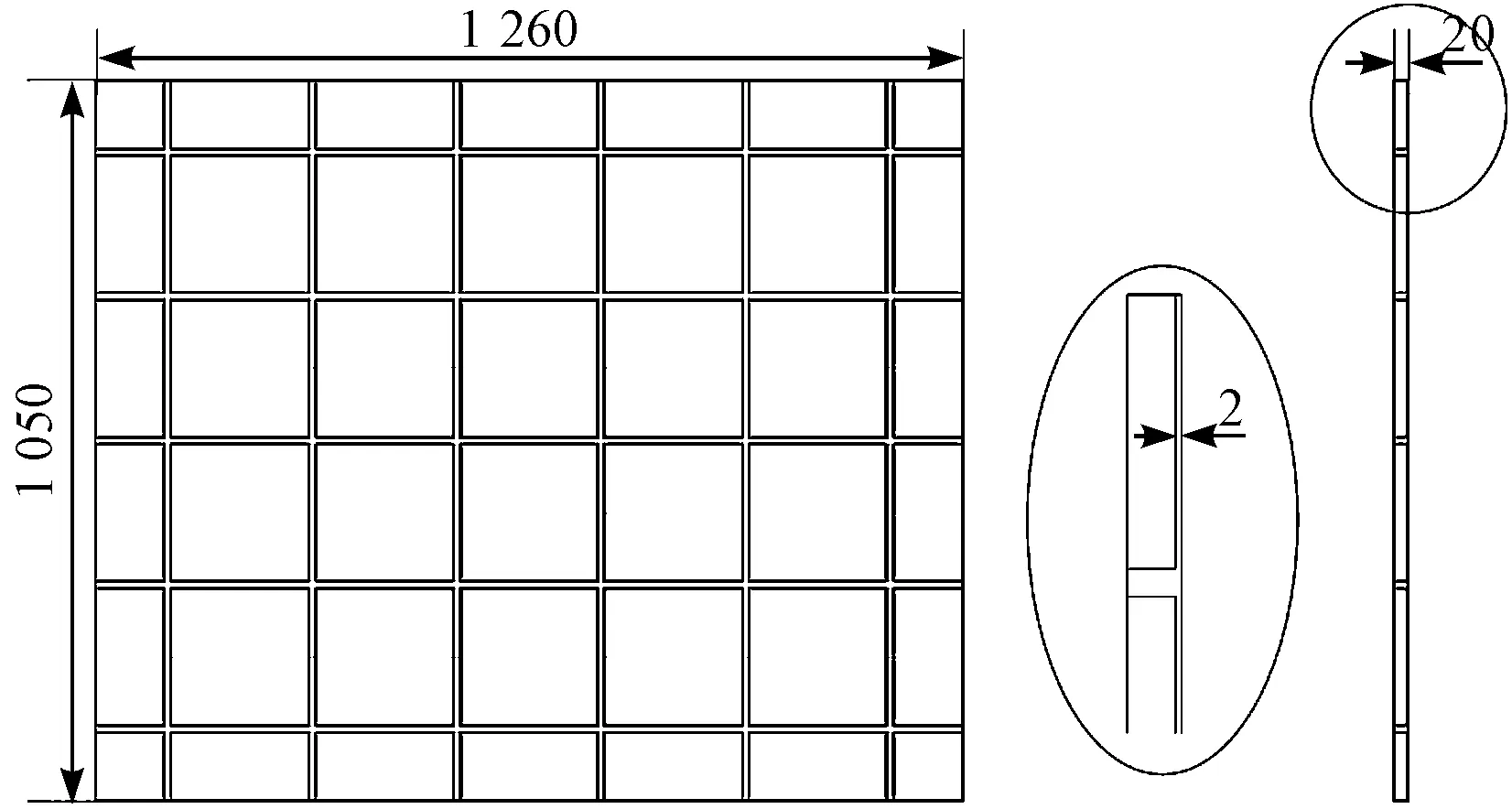
图6 带网格薄壁工件几何模型
在有限元软件中,笔者对图6模型进行模态分析,自动划分网格,材料设置为铝合金,加筋板的约束方式为底端为夹具的固定约束。
2.2 模态计算结果
网格剩余厚度2 mm薄壁工件的模态振型计算结果如图7所示。

图7 薄壁工件不同阶数模态振型
从图7薄壁工件模态振型可以看出,前两阶模态更偏向于薄壁工件的整体振动,从第十阶模态可以发现薄壁工件的网格处出现局部振动(出现这种现象的原因是该薄壁工件各部位刚度不均匀[15])。
这与实际结构是相符的,因为薄壁工件存在横向和纵向的筋肋,使得筋肋处厚度要比平板处大,改变了平板刚度的分布,从而出现局部振型[16]。
在实际铣削中,测得高频谐波成分复杂,存在750 Hz左右的峰值频率成分,极易与薄壁工件第十阶固有频率的共振区发生干涉,当高频谐波与带网格薄壁件发生共振时,薄壁件网格处的振动更为严重,极易造成铣削破坏、壁厚超差等严重问题。
因此,在使用ADD时,要把ADD作动器放在所铣削的网格处。
3 铣削振动抑制实验及分析
3.1 铣削振动抑制实验台
根据实际铣削薄壁件减重网格的情况,笔者为该实验选用了卧式铣床,搭建了铣削振动抑制实验台[17]。
其中,铣刀为4刃直柄铣刀,铣刀刃径为16 mm,柄径16 mm,刃长30 mm,铣刀总长70 mm。由于项目实际模型工件体积较大,受限于实验条件,该实验所用薄壁件经过简化处理,网格剩余厚度3 mm,铣削完成后可达到2 mm,网格大小135 mm×85 mm,工件整体尺寸300 mm×300 mm。
实验所用工件几何模型如图8所示。
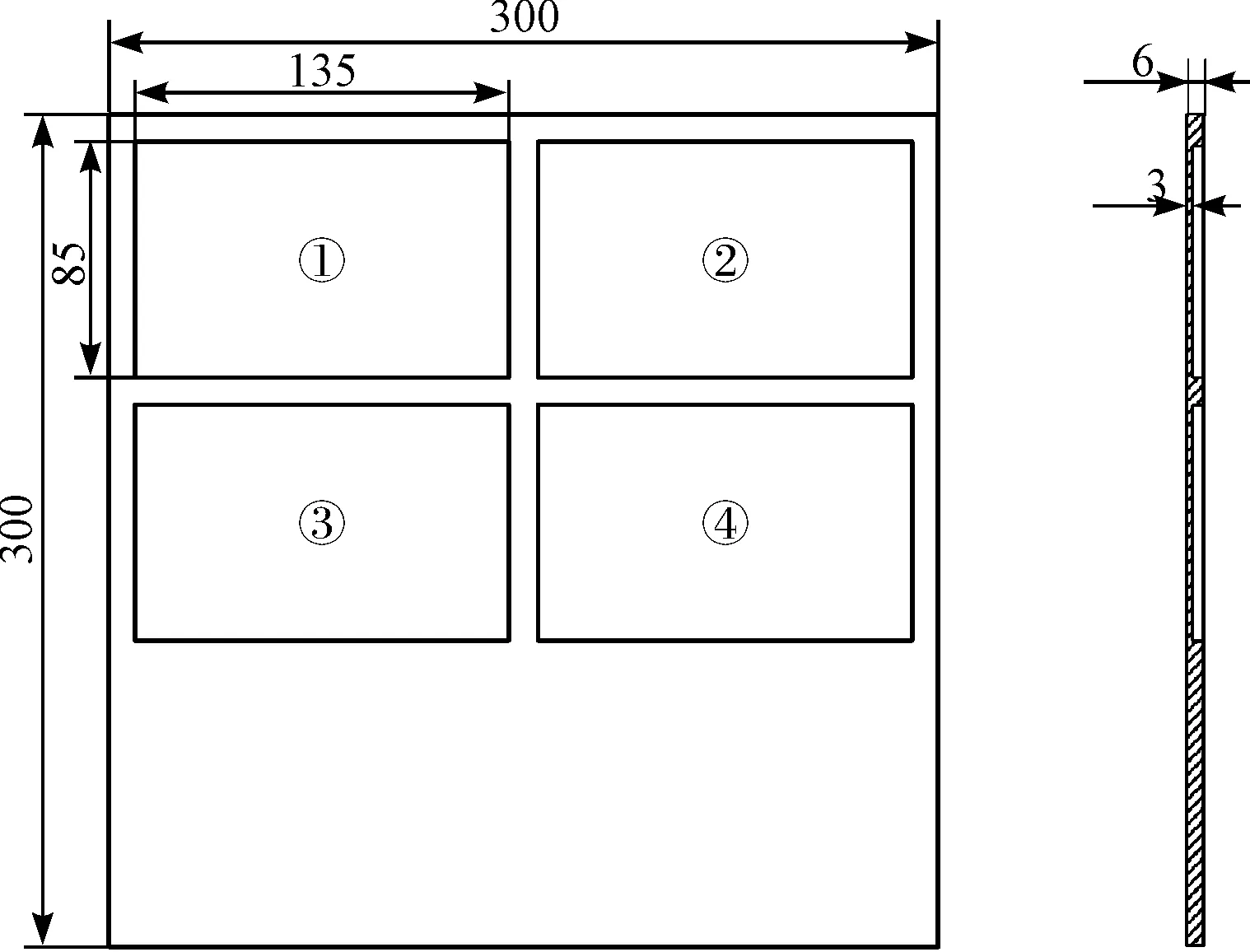
图8 实验所用工件模型
图8中,薄壁工件通过夹具固定在工作台上。在铣削网格面背面吸合ADD作动器,用加速度传感器测量铣削点振动。
实验采用M+P数据采集系统采集振动数据,采用LabVIEW编写的程序检测ADD作动器工作情况,采用NI数据采集卡来实现计算机与ADD数据的互通,使用ADD控制箱来调整ADD作动器的输出力。
铣削振动抑制实验台如图9所示。

图9 铣削振动抑制实验台
铣削振动抑制控制平台如图10所示。

图10 铣削振动抑制控制平台
3.2 不同主轴转速下的铣削实验
根据铣削振动抑制实验台所用卧式铣床的实际情况,笔者在铣刀工作转速分别为110 r/min、215 r/min、308 r/min、445 r/min的工况下铣削1号网格,进给深度0.5 mm,对比在不同转速下的振动抑制效果。
不同转速下的铣削振动抑制实验如图11所示。

图11 不同转速下的铣削振动抑制实验
在实验过程中,铣刀[18,19]从起点顺着进给方向运动,在铣削第一刀时不启动ADD作动器,直到铣刀延网格1长边铣完,采集铣削过程中原始振动数据;再将铣刀移至起点,在第一刀下方顺着进给方向进行铣削,第二刀铣削时启动ADD作动器,采集铣削过程中控制后的数据。
为获得最好的控制效果,ADD的反馈增益系数由功率放大器在实验时反复调节确定,最终反馈增益系数设置为270 V·s/m。
式(7)的变式为:
(10)
由表1可知,ADD作动器的输出力常数ga=4 N/V。根据式(7)的变式(10)可知,若将反馈增益系数gv设置为270 V·s/m,那么ADD对工件提供的阻尼值为1 080 N·s/m。即在该实验中,ADD向被控工件施加的阻尼恒为1 080 N·s/m。
不同主轴转速下,施加ADD前后工件振动情况对比如表2所示。

表2 不同转速下施加控制前后振动情况数据对比
不同转速下施加控制前后振动情况对比图如图12所示。
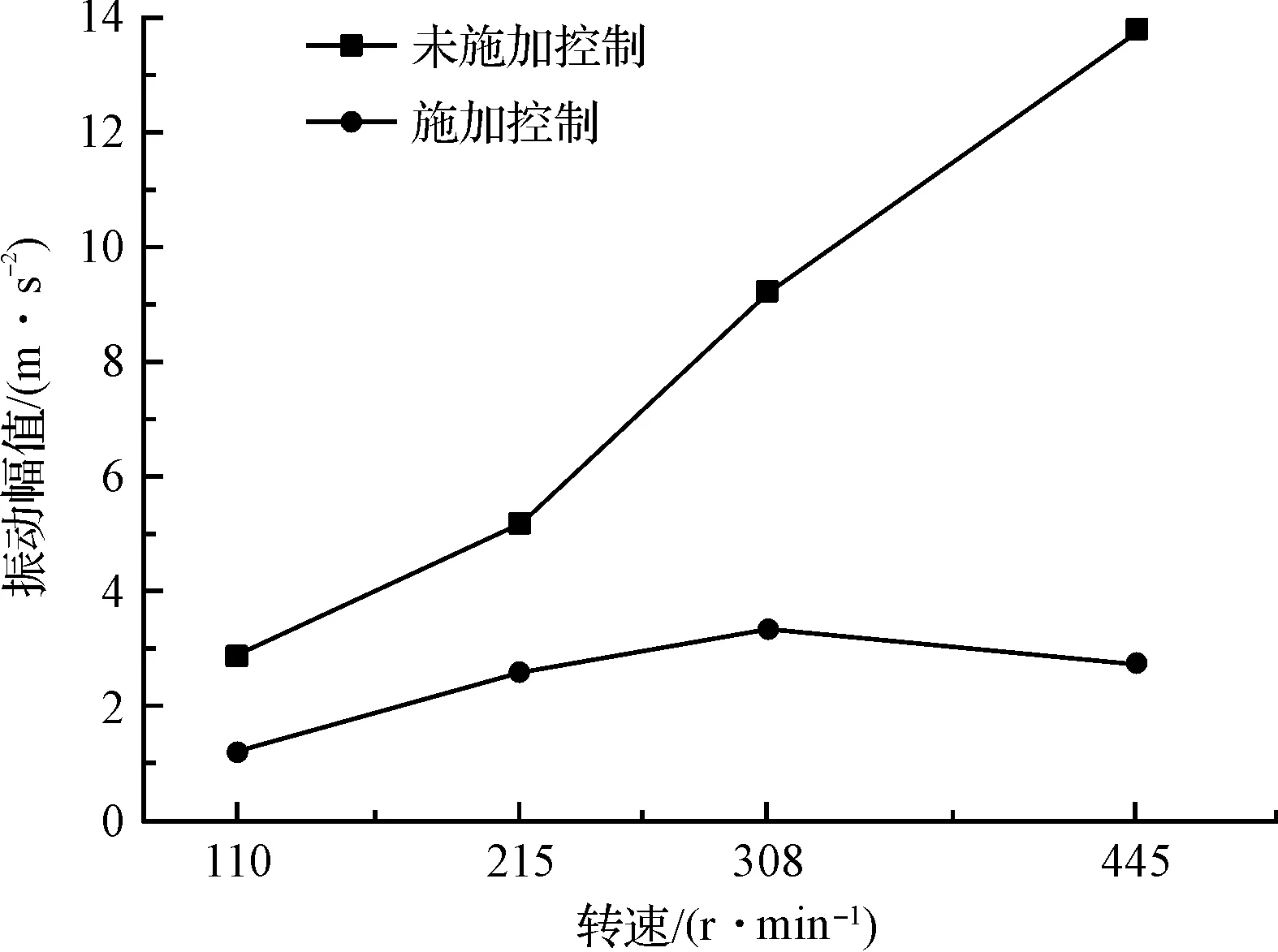
图12 不同转速下施加控制前后振动情况对比图
从表2及图12可以发现:施加ADD作动器后,薄壁工件在不同主轴转速下的铣削振动均得到抑制,这说明ADD的作用频带范围宽,可以抑制不同激振频率下的振动;随着铣刀转速的提高,薄壁工件的原始振动逐渐增大,但是ADD依旧能将振动控制在较小范围内,且在445 r/min工况下ADD抑制振动效果最好,降幅为79.98%。
实验所铣削的简化工件第一阶固有频率为745.68 Hz,而在445 r/min实验转速下所测工件的频谱图中,在750 Hz附近出现了波峰,这说明在445 r/min下进行铣削实验时,工件发生了共振现象。通过ADD作动器施加作动力后,工件在750 Hz下的振动大幅减小,有效避免了工件在445 r/min下发生共振的问题。
以445 r/min工况下的振动数据为例,笔者通过对此工况下时域波形及频域波形中控制前后的对比,分析主动控制效果。
445 r/min下时域波形如图13所示。
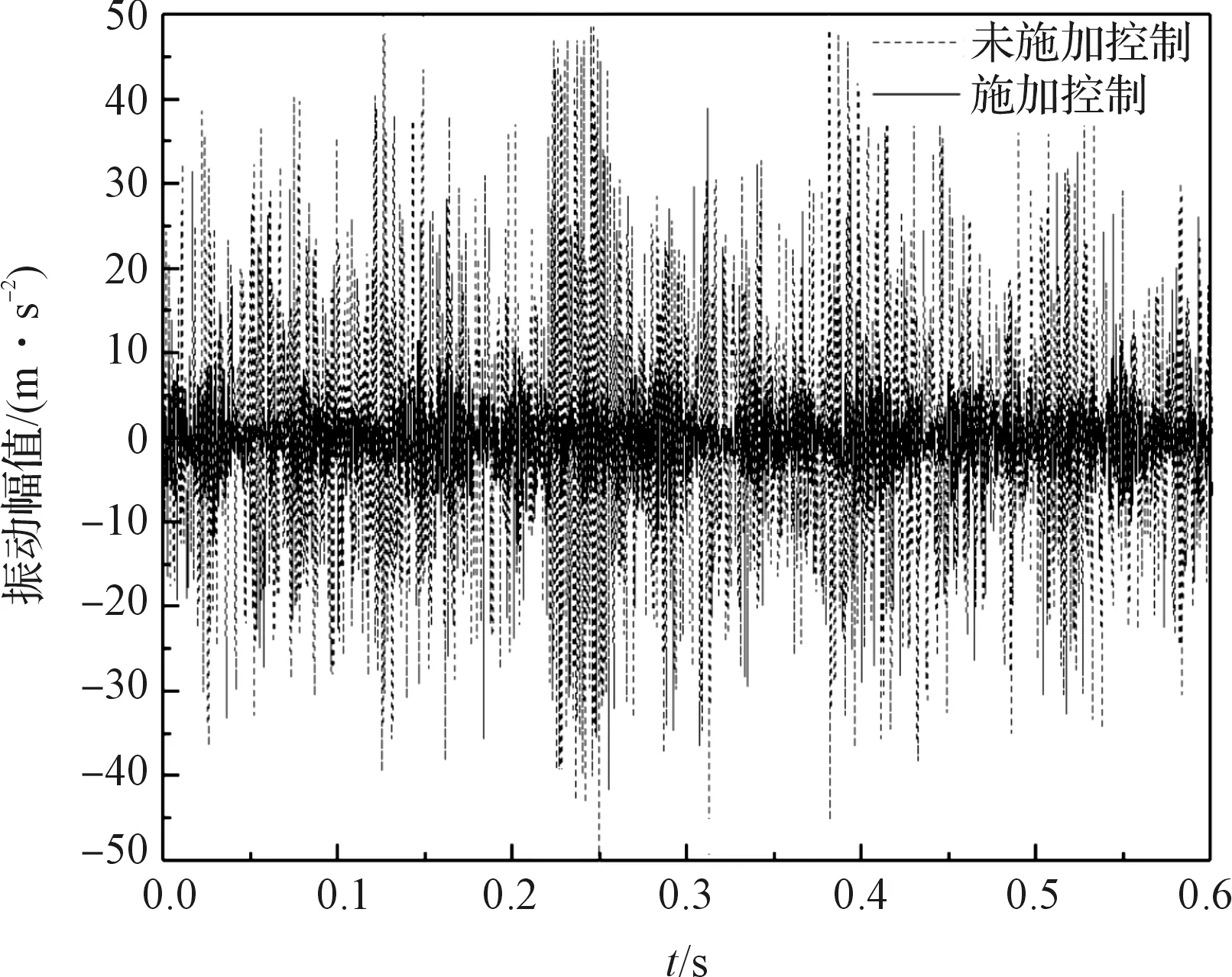
图13 445 r/min工况下时域波形
从图13中控制前后时域波形可以看出:相比于未施加控制时,施加控制后网格1处工件振动有了明显的降低,整个铣削过程更加平稳。这说明ADD可以有效抑制薄壁件铣削过程中的铣削振动。
445 r/min下频域波形如图14所示。
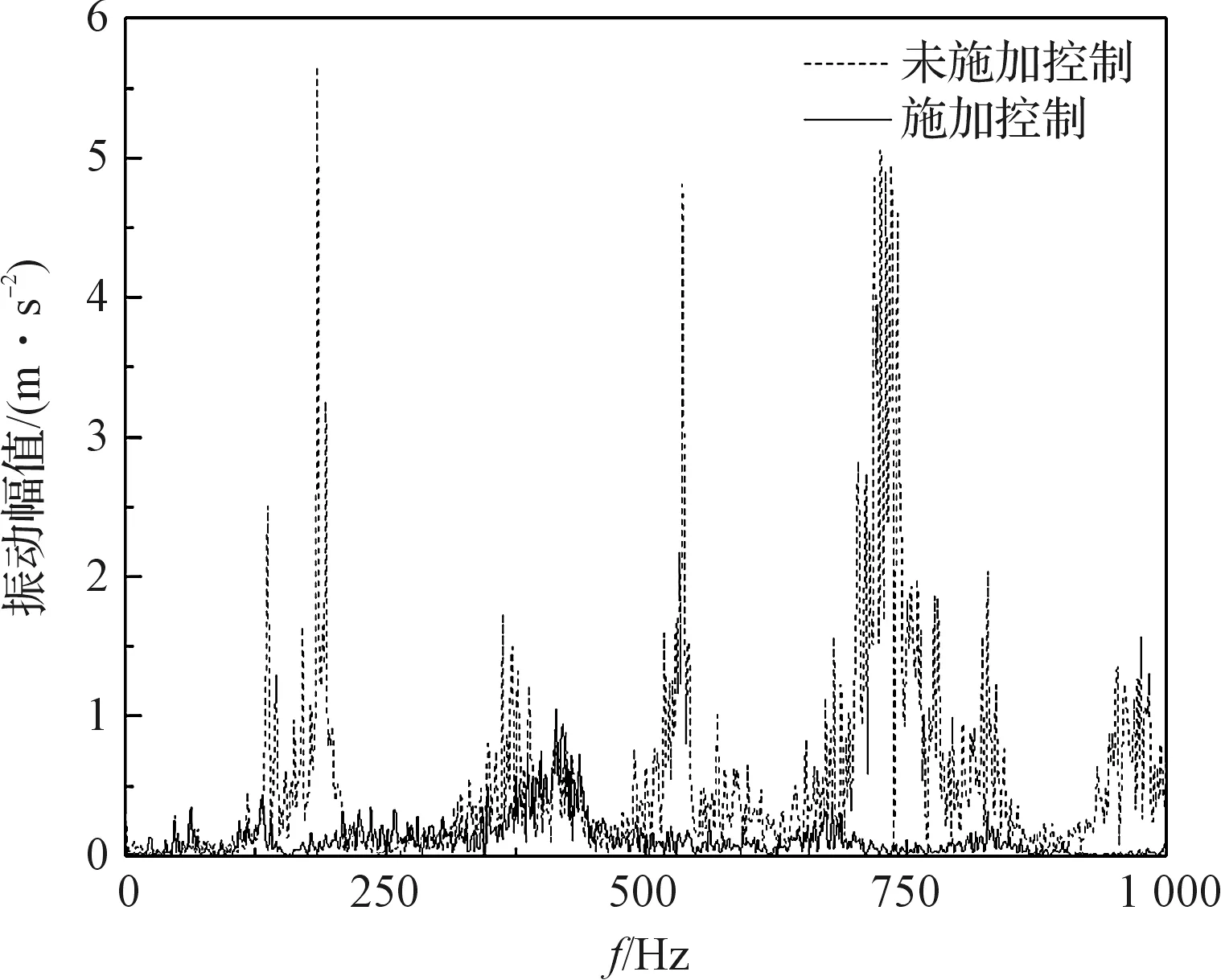
图14 445 r/min工况下频域波形
从图14中可以发现:铣削过程中,原始振动的频率成分复杂,主要频率集中在190 Hz~210 Hz,520 Hz~540 Hz,740 Hz~760 Hz等频率区间;
ADD对工件施加控制后,工件几乎在各个频率下的振动均有所减小,这进一步说明了ADD作用频带范围宽的特点,ADD不仅可以抑制不同激振频率下的振动,也可以对多频率的复杂振动起到一定的抑制作用。
3.3 不同网格剩余厚度下的铣削实验
在实际铣削过程中,工件网格处的材料不断去除,导致工件的模态参数发生变化。
为了研究ADD对不同网格剩余厚度的薄壁工件振动抑制效果,在转速445 r/min下,铣削网格剩余厚度分别为6 mm、5 mm、4 mm、3 mm的薄板,进给深度0.5 mm,笔者研究其在铣削过程中施加控制前后的振动情况(实验操作同上节实验相同)。
不同网格剩余厚度薄壁工件振动数据对比如表3所示。
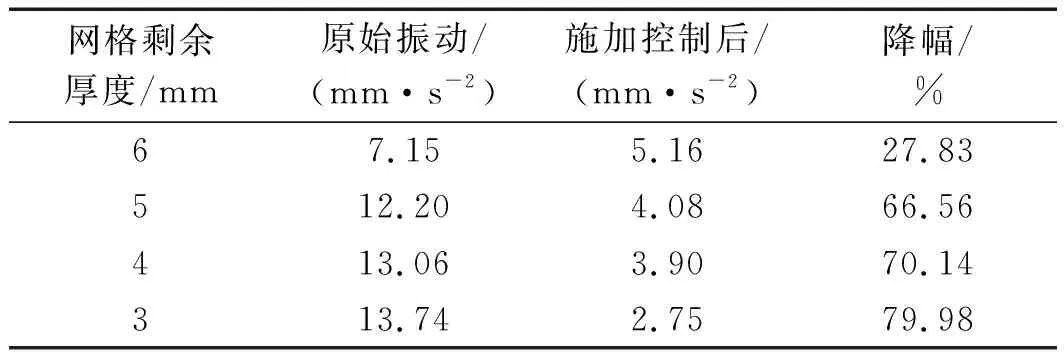
表3 不同网格剩余厚度薄壁工件振动数据对比
不同网格剩余厚度薄壁工件振动情况对比如图15所示。
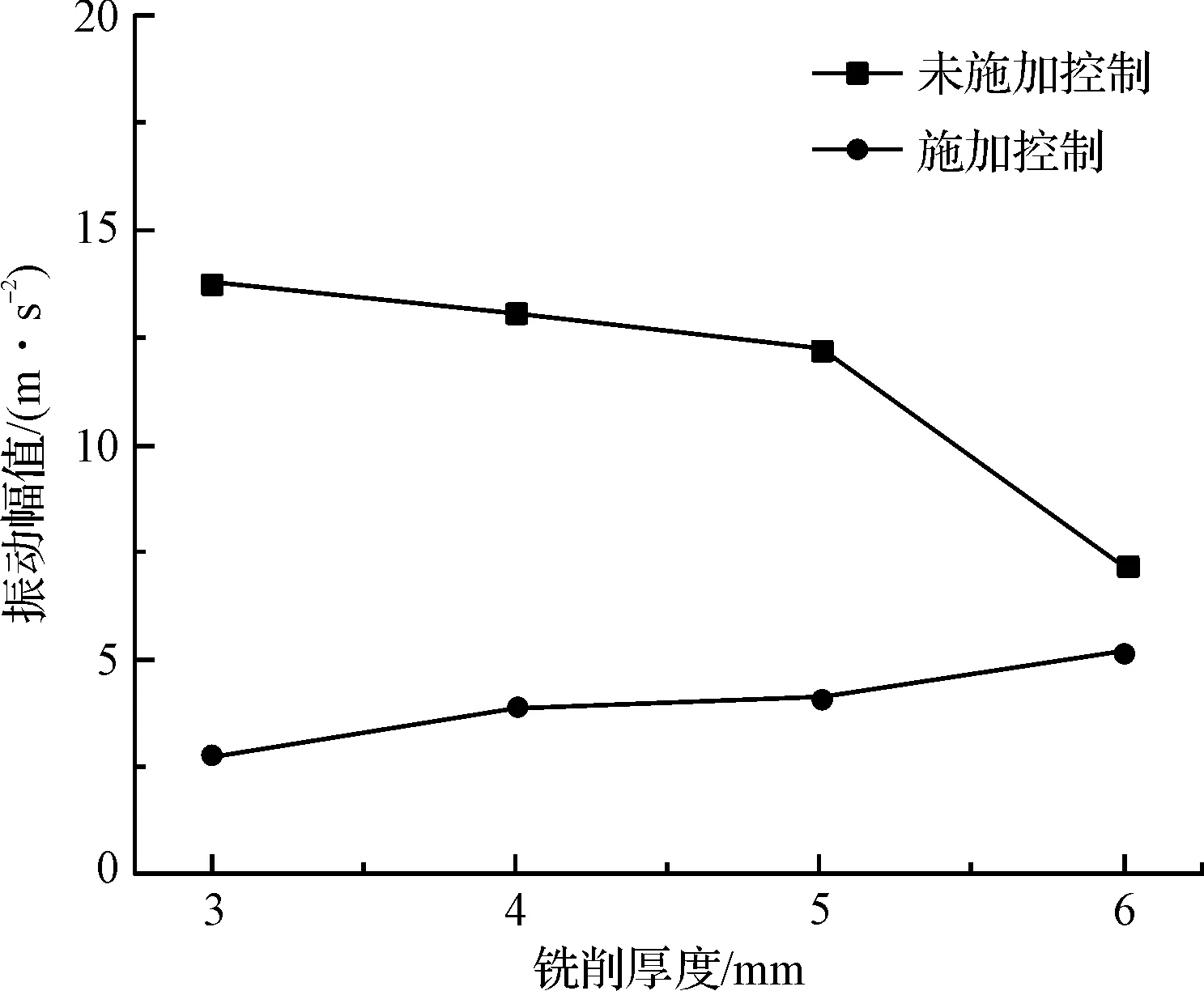
图15 不同网格剩余厚度薄壁工件振动情况对比
从表3和图15可以发现:施加ADD作动器后,不同网格剩余厚度的薄壁工件的振动均得到抑制;随着网格剩余厚度的降低,薄壁工件网格处的原始振动逐渐增大,但是ADD仍能够将振动保持在较小范围内;
其中,对剩余网格厚度3 mm的工件减振效果最好,其降幅为79.98%。这说明ADD在铣削过程中能够一直发挥其抑制振动的作用,对不同网格剩余厚度的工件均有效果。
3.4 施加控制前后粗糙度对比
为研究ADD对铣削工件表面质量的提高效果,笔者对网格剩余厚度3 mm工件的粗糙度进行了控制前后的对比。为避免测量结果的随机误差,在加工表面取3点进行粗糙度测量后,取其平均值作为测量结果。
控制前后的测量结果如表4所示。
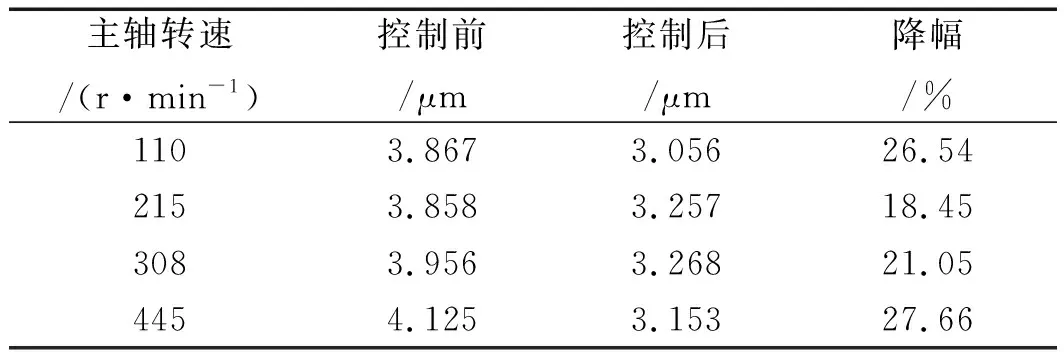
表4 控制前后工件粗糙度数据对比
通过表4实验数据可知:在施加控制后,加工工件在各个转速下的粗糙度均有所下降;其中,在445 r/min工况下,表面粗糙度降幅最大,降幅达到27.66%。
该实验结果说明:施加控制后可以降低铣削工件的表面粗糙度,提高工件的表面质量。
4 结束语
基于直接速度反馈控制算法,笔者将ADD应用到薄壁件铣削加工系统中,运用ANSYS软件对薄壁件进行了模态分析,并通过搭建实验台进行了薄壁件铣削实验,以此来对ADD的作用效果进行验证。
研究结果表明:
(1)ADD具有作用频带宽的特点,对多个主轴转速下的铣削振动均有抑制效果,对多频率的复杂振动也有振动抑制效果,最大振动降幅为79.98%;
(2)ADD对不同网格剩余厚度的薄壁工件均有振动抑制效果,即在工件由厚到薄的铣削过程中,ADD均能发挥其作用;
(3)ADD能提高薄壁工件的表面质量,降低薄壁工件表面粗糙度,粗糙度最大降幅为27.66%。
在后续的研究中,笔者将探索ADD自动调整增益的方法,避免在铣削过程中的人工调整增益,从而提高铣削的效率。
