关注细节梯度 渗透情景育人——记《等差数列的性质（第一课时）》的磨课实践

浙江省温岭市新河中学 江 杨 （邮编：317502）

笔者参加了一次地区的高一教学活动，并上了一节公开课《等差数列的性质（第一课时）》，下面回顾这节课的“打磨”过程与反思所得.

一拿到课题，本着激发探究的兴趣又体现新课程的理念，想构建一个情境引入，但实在太难，难在性质的探究更多是从具体的习题中得到，而非来自生活实际情境.由此感觉好像只能走“讲授—例题—练习—总结”的“老套路”，但公开课这样缺乏新意，很无奈但也要转换思路，于是进行了第一次整体课题设计的“打磨”，最后经过与组内老师探讨和反复思考确定下来走“例题（问题）—探究—练习—总结”的“新路子”.并考虑一题多变，变式到底，边变边练，让问题的提出和解决显得自然而然，探究得出性质变得水到渠成.

1 第一次教学片断（实录）

回顾等差，引入例题.已知数列{ }an为等差数列，a2＝5，a10＝21，求公差d（学生大多用基本量法求得）.

点评以例题入手，开门见山，既是例题又是问题，不走枯燥推导性质、先讲授知识，后讲解例题的“老套路”.

问1有无其他方法得出公差d?

生：两数直接相减得16，除以下标的差8，所以公差为2.

（肯定的同时引导学生观察、推广，得出性质1）

性质1通项公式一般式：an＝am+_____（m、n∈N*）⇒d＝______.（课前印发了学案，留有性质的填空，同时PPT展示）

问2你会证明这个一般式吗？（对猜想的性质作严格的证明）

变式1在等差数列{an}中，若am＝n，an＝m（m≠n，m、n∈N*），求am+n.

（2）求a4+a8

问3你有什么发现？

生：a2+a10＝a4+a8＝26.

问4你能推广得出相应性质吗？（引导学生发现，总结，归纳出性质，证明）

性质 2对称性：若m+n＝p+q（m、n、p、q∈N*），则______＝______；

特 别 地 ，若m+n＝2t（m、n、t∈N*），则am+an＝______.

（学生填空，后PPT展示）

点评性质2是等差数列中非常重要性质——下标和相等，对应的两项和也相等.这里重在学生自己发现规律，总结归纳出性质.

变式2若数列{an}为等差数列，a1+a2+… +a9＝72，则a2+a4+a9＝______.

变式3若数列{an}为等差数列，a1+a4+a7＝15，a2a4a6＝45，求公差d.

（通过两道变式训练，达到应用巩固目的.变式2实际上是将性质2推广至多项）

（3）将{an}中的第1项，第7项，第13项……抽出组成新的数列{bn}的第1项，第2项，第3项……，问：{bn}是否为等差数列？证明你的结论.

生：是的.

问5为什么？你能证明吗？

（学生感觉想当然，一时无从下手，引导学生回到定义，关键找到bn＝a3n-1，n∈ N*）

变式4若{an}、{bn}为等差数列，下列数列为等差数列吗？

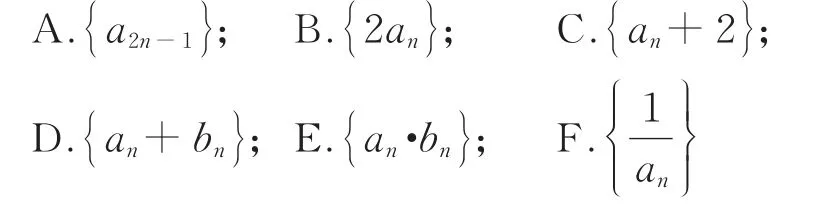
变式5已知{an}为等差数列，a1+a2+… +a6＝10，a7+a8+ … +a12＝70，则

a13+a14+ … +a18＝______.（由第（3）小题结论可很快得出三者成等差关系）

性 质3若{an}，{bn}等 差 ，则 ①ak，ak+m，ak+2m…（k，m∈N*）也为等差数列；②{an+C}，{λan}，{an+bn}即___________也为等差数列；

③a1+a2+ … +an，an+1+an+2+...a2n，a2n+1+a2n+2+…+a3n，…仍成等差数列.

点评为了引出性质3的①②③性质，考虑从特殊出发，先有①，再有②，后有③，层层递推，顺势而为，让性质的得出自然而然.

至此，这节课的内容已完成，然后让学生对知识层面进行总结再上升到数学思想.

2 第一次课后点评

以上是第一次校内公开课，课后教研员和组内老师从细节出发提出了很多宝贵的意见，以下是主要的几点：

（1）考虑到学生层次是否内容量太大（所教高中层次处在县市中游水平）；

（2）是否可以降低难度，设定梯度.例如可以将变式1中字母改为特殊值；

（3）性质3的③涉及求和，应在学好等差数列前n项和后去涉及，是否不应在本节出现.

3 第二次教学片断（摘录）

教研员和组内老师给予了中肯的意见和研讨，基于以上建议，进行第二次“打磨”：

（1）将变式 1：“在等差数列{an}中，若am＝n，an＝m（m≠n，m、n∈N*），求am+n”改 为“ 等差 数 列{an}中，若a10＝100，a100＝10，求 公 差d及a110”，再此基础上再提问：“在等差数列{an}中，若am＝n，an＝m（m≠n，m、n∈N*），求am+n”.学生在具体数字中能快速解决，字母只作延伸，点醒学生即可，课堂不再演算.

（2）变式2和3考虑也设定坡度，并进行修改.

变式2“若数列{an}为等差数列，a1+a2+… +a9＝72，则a2+a4+a9＝______”改 为 ：“ 若数列{an}为等差数列，a4+a5+a6＝72，则a5＝_____;a2+a4+a9＝_______”.设定了台阶“求a5”，同时将条件中的前n项和调整得更简单，更符合本节课题范围.

变式3“若数列{an}为等差数列，a1+a4+a7＝15，a2a4a6＝45，求公差d”改 为 ：“ 在 等 差 数列{an} 中 ，a2+a4+a6＝15，a2a4a6＝45，且a2、a6为方程x2-mx+n＝0的两个实根，求m、n的值及公差d”.增加了韦达定理的关联，设定了台阶“求m、n”，这里还预设了一个提问：“这里的m、n指什么”，只要迈上了这个台阶，就能容易得出a2、a6和公差d，相较于原题直接求公差d，变得简单了很多，符合所教对象的层次.

（3）第（3）小题考虑学生不易归纳出bn＝a3n-1，所以直接将第（3）小题“{an}中的第1项，第7项，第13项……抽出组成新的数列{bn}的第1项，第2项，第3项……，问：{bn}是否为等差数列？证明你的结论.”改为：“数列{bn}的通项满足bn＝a3n-1，证明：{bn}为等差数列.”再让学生分析{bn}是怎样的数列？

4 第二次课后点评

修改后再次在校内上课，总体感觉与预想的较为接近了，组内老师也基本肯定，但也有老师提出总觉得去地区上公开课引入不够出彩，然而由于《等差数列的性质（第一课时）》这一课题比较局限性，大家也没有什么好建议，因为平时教学中也都没有这方面的情景引入，通常还是接着上一节《等差数列》进行引入，如何才能“画龙点睛”呢？于是在苦思冥想后进行第三次“打磨”，决定将个人的一次南京旅行和爱国教育与本节例题有机结合，作为课题引入.

5 第三次公开课片断（实录）

师：同学们，前面已经学习了等差数列的概念，今天来研究下它的性质.先从一段旅行谈起，今年春节我和家人去了南京旅游，这次旅游给我印象最深的是南京大屠杀纪念馆，30万同胞的生命在短短几天被杀害（PPT展示旅游时拍下的照片），那一幕幕触目惊心的照片深深扎在我心头，其中回忆最深的是纪念馆出口一个不起眼的角落，那里在不停滴水，每滴水的间隔是d秒，每过d秒就会出现一个头像，代表着一个中国人被杀害，我被深深震撼到了，大家想知道d为几秒吗？想知道日本侵略者是多么惨无人道地杀害平民百姓吗？

生：想（学生低沉地回答）

师：老师换一种形式给出答案.问题：假如第三个人被杀害时，秒针指向是时钟的6刻度，那么当第七个人被杀害时，秒针还没走过一圈，指向的是时钟的54刻度，你们能算出是每过几秒杀一个人吗？谁能最快地算出d？抽象成数列问题怎么表示？

生1：将两数直接相减得48，除以下标的差4，所以公差为12，即12秒.

生2：抽象为数列问题：{ }an为等差数列，a3＝6，a7＝54，求公差.

（引导学生观察、推广，得出性质1）

性质1通项公式一般式：an＝am+_______（m、n∈N*）⇒d＝_______（课前印发了学案，留有性质的填空，同时PPT展示）

问2你会证明这个一般式吗？（对猜想的性质作严格的证明）

变式1等差数列{ }an中，若a10＝100，a100＝10，（1）求公差d及a110；

再提问在等差数列{ }an中，若am＝n，an＝m（m≠n，m、n∈N*），求am+n呢？

（2）求a5及a4+a6；

师：你有什么发现?

引导学生发现，总结，归纳出性质2并证明

性质2对称性：若m+n＝p+q（m、n、p、q∈N*），则______＝______；

特 别 地 ，若m+n＝2t（m、n、t∈N*），则am+an＝______.

（学生填空，后PPT展示）

变式2若数列{ }an为等差数列，a4+a5+a6＝72，则a5＝______，a2+a4+a9＝______.

变式3在等差数列{ }an中，a2+a4+a6＝15，a2a4a6＝45，且a2、a6为方程x2-mx+n＝0的两个实根，求m、n的值及公差d.

师：这里的m、n指代什么？

生：两根和与积，即a2+a6，a2·a6.

（通过这个提问引导，学生很快解决）

变式4{an}为等差，a1+a4+a7＝15，a2a4a6＝45，求an.

（在变式3的基础上，提高难度，课堂上点到为止，留给学生课后思考）

（3）数列{bn}的通项满足bn＝a3n-1，求证：bn也为等差数列.

师：你会证明吗？从中你发现什么？

（引导学生发现，总结，归纳出性质，证明）

变式5若{an}为等差数列，下列数列为等差数列吗？

A.{2an}； B.{a2n-1}；

C.{an+2}；D.{an+bn}

性 质3若{an}、{bn}等 差 ，则 ①ak，ak+m，ak+2m…（k、m∈N*）也为等差数列 ② {an+C}，{λan}，{an+bn}即____________也为等差数列.

（原来的变式5涉及求和删去）

至此，这节课的内容已完成，同样让学生对知识层面进行总结再上升到数学思想.最后，升华到爱国主义育人理念的渗透，我低沉地说：“愿逝者安息，让我们勿忘国耻”，同时为了前后呼应，PPT上展示出那个“12秒区域”的图片和文字说明以及国家公祭日等图片，此时无声胜有声.

6 课堂成功与反思所得

经过三次“打磨”和试上，最后在地区上课时取得非常成功的课堂效果，得到了同行们肯定与鼓励.

回顾整个磨课实践，感触颇深.现在的学生很多只会简单的套用公式，不会探究，不会转化问题解决，这与我们的教学方式有很大关系.传统的教学以教师为主线，强调基础知识的传授，常常采用满堂灌，特别是一些习题课，懒于体现学生的主体性，锻炼他们探究能力，更不提的人文情感教育的渗透.实际上，都是教师高高在上，疏于“理政”的结果导致的，只要创造性的使用教材，融入自己的智慧，同时群策群力，广纳良言，在教学过程多想善思，用好引趣、激疑、探究等手段，一定能提高学生的“究知”能力，能更好地备出一节有效课.

前苏联教育学家苏霍姆林斯基说过：“教师进行劳动和创造的时间好比一条大河，要靠许多小的溪流来滋养它”.一节真正有品质的课需要为之倾心费力，只有潜下心来，专心“打磨”每个细节，才能得到夺目的“玉器”，正所谓：“玉不琢不成器”.