错在哪里

1 安徽省合肥市肥东县城关中学

王东海（邮编：231600）

题目已知1-3a，2a，1+3b成等比数列，则16a+18b的取值范围是______.

错解由于1-3a，2a，1+3b成等比数列，因此

所以(a，b)应在椭圆上，注意到4a2+9b2＝1与16a+18b＝±10相切.而由于 1-3a，2a，1+3b成等比数列，故a≠ 0，从而因此16a+18b≠±6.

综 上 得 16a+18b∈[-10，-6)∪(-6，6)∪(6，10].

解答错了！错在哪里？

这是我校近期的模考题，上述解答看似天衣无缝，感觉没有问题，其实是错误的.这里很多学生认为当a＝0时，1-3a，2a，1+3b不成等比数列，故椭圆4a2+9b2＝1上的点)不符合条件，从而16a+18b≠±6.所以应除去±6.

正确解法

正解1在错解中将“故a≠0，从而因此16a+18b≠±6.”去除，并将答案改为：

综上得16a+18b∈[ ]-10，10.

正解2由于4a2+9b2＝1，可令因 此 16a+18b＝8cosθ+6sinθ＝10sin(θ+φ)，

2 浙江省江山中学

徐丽峰（邮编：324100）

题目若不等式|2x+1|-|x-a|≥a对任意的实数x恒成立，则实数a的取值范围是.

错解若x≥a，①当时，原不等式化简为x+1≥0，显然成立时，原不等式化简为-3x-1≥0，显然成立，所以a∈R.

解答错了！错在哪里？

上述解答看似分类讨论过程完整，答案也正确，其实是有问题的.错解中缺少与a两者大小比较，这会导致某一类讨论没有意义，从而产生问题.比如第一类“若x≥a”讨论中，若a＞的情况没有讨论的意义，此时原不等式转化为x+a+1≥a，解得a≥-1，所以

正 解 1记g（x）＝|2x+1|-|x-a|，原 不等式成立等价于g（x）min≥a.

正解2原不等式等价于|2x+1|≥|x-a|+a.将不等式问题转化函数图象问题，即函数f（x）＝|2x+1|的图象在函数g（x）＝|x-a|+a的图象上方或者除公共点，f（x）图象其他点都在g（x）的图象上方.特别地，这两个函数图象都像“V”形，顶点坐标分别为（-随着a的增大，函数g（x）的图象形状保持不变，顶点沿直线y＝x向上运动.由图1可知，只需满足不等式即可，解得

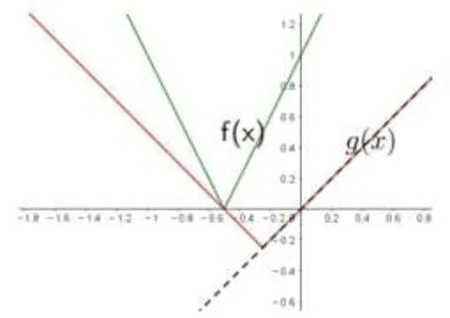
图1