关于垂足三角形的几个极值问题

重庆市长寿龙溪中学 吴 波 陈骑勇 （邮编：401249）

定义1[1]如图1，P为△ABC所在平面内任一点，从P向△ABC的三边所在直线分别作垂线，垂足分别为P1、P2、P3，把 △P1P2P3叫做点P关于△ABC的垂足三角形.

图1

文[2]中证明了：在△ABC的垂心，外心，内心，重心这四心中，垂心的垂足三角形的内切圆半径最小.联想到几何中著名的Schwarz定理“锐角三角形周长最短的内接三角形是它的（垂心的）垂足三角形”（文[3]中将此列为第90个问题），文[2]中提出如下.

猜想[2]在锐角△ABC中，过其内部一点向三边所在直线作垂线，三个垂足构成的三角形中，垂心的垂足三角形的内切圆半径最小.

本文将否定这个猜想.并探讨关于垂足三角形的另外几个极值问题.

为表述方便，本文约定：△ABC三边长按习惯记为a、b、c，面积为S，外接圆半径为R，内切圆半径为r.点P关于△ABC的垂足三角形△P1P2P3（可以是退化的）的面积为SP，周长为LP，外接圆半径为RP，内切圆半径为rP.

先给出几个引理：

引理1[1]点P到△ABC的外心的距离为d，则

其中当点P在△ABC外接圆外时取“+”，当点P在△ABC外接圆内时取“-”.

由此易知：当d为定值时，SP也为定值.即有

推论1[1]当点P在△ABC外接圆的半径为d的同心圆上运动时，其垂足三角形的面积SP为定值

当点P在△ABC外接圆上时，有d＝R，则SP＝0，即此时P1、P2、P3共线.此即 Simson定理.

而点P在△ABC外接圆内时，0≤d＜R，由此可推得三角形中的经典结论：

推论2[1]点P在△ABC外接圆内时有SP≤当且仅当P取△ABC的外心时，等号成立.

注外心的垂足三角形即是△ABC的中点三角形.

如图1，PA、PB、PC将△ABC分为三个三角形，由此可得下面这个熟知结论：

引理2如图1，P为△ABC内或边上任意一点，则a|PP1|+b|PP2|+c|PP3|＝2S.

下面我们否定前面的猜想.事实上，我们有

定理1点P在△ABC内时，其垂足三角形的内切圆半径以0为下确界，但并无最小值.

证明如图1，当点P→A时，P到△ABC外心的距离d→R.由引理1推论1知：此时SP→0（在图1中表现为△P1P2P3的两边P1P2与P1P3趋于重合）.

而P→A时，有|P2P3|→0，|P1P2|→hA，|P1P3|→hA（如图1，hA指BC边上的高AD）.此时△P1P2P3的周长LP＝|P1P2|+|P2P3|+|P3P1|→2hA.

则P→A时，△P1P2P3的内切圆半径→0.

虽 然 有rP→0，但rP≠0（因 为SP≠0）.这 表明：定理1结论成立.证毕.

在锐角三角形内一点的垂足三角形中，由引理1推论2知：外心的垂足三角形的面积最大；而由Schwarz定理知：垂心的垂足三角形的周长最小.而正三角形四心重合，结合内切圆半径公式即得：

定理2当正三角形内的点P取正三角形中心时，其垂足三角形的内切圆半径最大.

对于一般的三角形，当其内的点P在什么位置时其垂足三角形的内切圆半径最大？估计这是一个比较困难的问题.

下面再看关于垂足三角形的另外几个极值问题.

定理3点P为△ABC所在平面内任意一点，当点P取△ABC的内心时其垂足三角形的外接圆半径最小.

文[4]仅对点P在锐角△ABC内这种情形分三类进行了证明.这里将其推广到一般的三角形且点P也是任意的.

证明设P关于△ABC的垂足三角形△P1P2P3的外心为Q，△P1P2P3的外接圆半径为RP.如图2、图3，过Q作△ABC三边所在直线的垂线，垂足分别为Q1、Q2、Q3.

图2

图3

如图2、图3，因△P1P2P3的外接圆与△ABC三边所在直线都有公共点，由“垂线段最短”有：

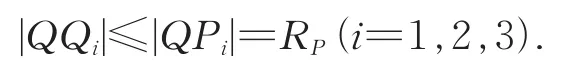
因此a|QQ1|≤aRP，b|QQ2|≤bRP，c|QQ3|≤cRP.三式相加得：

（1）如图2，当圆心Q在△ABC内或边上时，①式结合引理 2有：（a+b+c）RP≥2S.

因|QQi|≤|QPi|＝RP（i＝1，2，3）中诸等号都成立，当且仅当△P1P2P3的外接圆与△ABC三边均相切.注意到点P在△ABC内或边上，此时△P1P2P3的外接圆即是△ABC的内切圆，也即是当且仅当点P为△ABC内心时等号成立.

（2）当圆心Q在△ABC外时，引理2中的等式左边的某些项要改变符号才成立.比如，对于图3中的情形，易知此时：S△QAB+S△QBC-S△QCA＝S.也即是有：

由①，②两式可知：

（a+b+c）RP≥a|QQ1|+b|QQ2|+c|QQ3|≥a|QQ1|-b|QQ2|+c|QQ3|＝2S.

当点P不在图3中的区域，而在△ABC外的其它区域时，类似可证此不等式成立.

综合（1）（2）可知：定理 3结论成立.证毕.

熟知：三角形的Fermat点到三个顶点的距离之和最小.对偶地，想知道：当△ABC内的点P在什么位置时，它到△ABC三边所在直线的距离之和取最值？

经过探讨，得到如下结论：

定理4记△ABC三边上的高分别为hA、hB、hC，△ABC内的点P的垂足三角形为△P1P2P3.则

（|PP1|+|PP2|+|PP3|）sup＝max{hA，hB，hC}，

（|PP1|+|PP2|+|PP3|）inf＝min{hA，hB，hC}.

证明不妨设a≥b≥c.则hA≤hB≤hC.结合引理 2，有

a（|PP1|+|PP2|+|PP3|）≥a|PP1|+b|PP2|+c|PP3|＝2S.所以

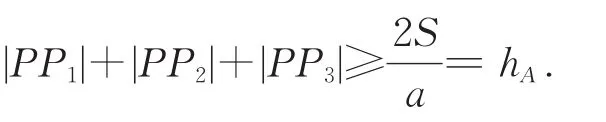
当且仅当△ABC为正三角形时取等，否则严格不等.

如图1，令P→A.则|PP2|→0，|PP3|→0，因此有

a（|PP1|+|PP2|+|PP3|）→a|PP1|→a|PP1|+b|PP2|+c|PP3|.

结合引理2即有

综上可知，（|PP1|+|PP2|+|PP3|）inf＝hA.

对非等边三角形，当P趋近于最大角顶点时|PP1|+|PP2|+|PP3|趋近于下确界.

类似可证：（|PP1|+|PP2|+|PP3|）sup＝hC.

对非等边三角形，当P趋近于最小角顶点时|PP1|+|PP2|+|PP3|趋近于上确界.证毕.

由Schwarz定理知：锐角三角形内一点P的垂足三角形的周长在P取垂心时最短.那么什么时候其垂足三角形的周长最长呢？利用定理4可以求得其周长的上确界.即

定理5记△ABC三边上的高分别为hA、hB、hC，△ABC内的点P的垂足三角形△P1P2P3的周长的上确界为 max{2hA，2hB，2hC}.

证明不妨设a≥b≥c，则hA≤hB≤hC.如图1有

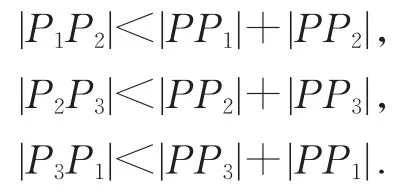
三式相加可知周长

LP＝|P1P2|+|P2P3|+|P3P1|＜2（|PP1|+|PP2|+|PP3|）.

结合定理 4有LP＜max{2hA，2hB，2hC}.

如 图1，令P→C，则|P1P2|→0，|P2P3|→hC，|P3P1|→hC.因此有

LP＝|P1P2|+|P2P3|+|P3P1|→2hC.

综上可知：（LP）sup＝2hC＝max{2hA，2hB，2hC}.

当P趋近于最小角顶点时周长趋近于此上确界.证毕.

定理6点P为△ABC内任意一点，则当P取△ABC重心时，P到△ABC三边的距离之积的值最大且最大值为

证明如图1，由引理 2：a|PP1|+b|PP2|+c|PP3|＝2S.结合均值不等式有

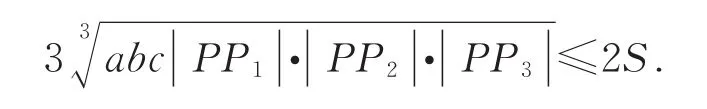
等号成立当且仅当a|PP1|＝b|PP2|＝c|PP3|——如图1，也即是S△PBC＝S△PCA＝S△PAB时.显然此时点P为△ABC的重心.证毕.

当点P无限趋近于△ABC的某条边时，点P到此边的距离无限趋近于0.因此P到△ABC三边的距离之积可无限趋近于0.

关于垂足三角形还有如下两个极值问题，有兴趣的读者可继续探讨：

问题1△ABC内的点P的垂足三角形的外接圆半径何时取最大值？

问题2△ABC内的点P的垂足三角形的内切圆半径何时取最大值？