单层轮辐式索网结构形状确定研究
2022-02-28张佳毅邹贻权
张佳毅,邹贻权
(湖北工业大学土木建筑与环境学院,湖北 武汉 430068)
近年来随着我国综合国力的增强和计算机技术的进步,结构理论分析方法和施工技术等得到长足的进步,由于我国体育事业的发展,各类轻质、高强、大跨建筑随之出现。因索结构具有自重轻、节省材料、施工便捷能够适应多样化的建筑造型等优点引起了广大设计人员的兴趣,越来越多的应用索结构屋盖的大型体育场馆相继出现[1]。但索结构属于柔性张拉结构,必须施加一定的预应力才能形成承受外部荷载所需的刚度和形状[2]。因此确定索结构零状态、初始态、荷载态的几何形状是索结构的结构设计的过程中需要解决的关键问题。索结构其类型主要有:单层索系、双层索系、索桁体系等结构体系。其中单层轮辐式索网结构应用得最晚,该结构形式在贾比尔.艾哈迈德体育场才得到首次应用。通过贾比尔.艾哈迈德体育场曾无法通过验收的现象可以从侧面体现单层轮辐式索网结构的相关理论方法与施工技术仍有所欠缺[3]。在单层轮辐式索网结构的相关研究中,其更多的是研究改进力学找形方法并利用有限元分析软件加以实现。
在现有的找形方法用于索杆体系时常使用平衡矩阵理论[4],力密度方法[5]和动力松弛方法[6]进行计算时。这些方法的研究主要应用于索膜结构和索网结构,针对单层轮辐式索网结构的效率较低。
随着计算机技术的发展,越来越多的设计人员开始使用参数化设计工具进行设计。相比于传统有限元分析软件,RHINO和Grasshopper所提供的参数化平台可以大大地提高设计建模和分析的效率,更易实现单层轮辐式索网结构形状确定的找形方法[7]。
本文拟对单层轮辐式索网结构(图1)的找形方法和原理进行较为全面的阐述,并在参数化设计平台RHINO和Grasshopper上结合算例证明方法的适用性。
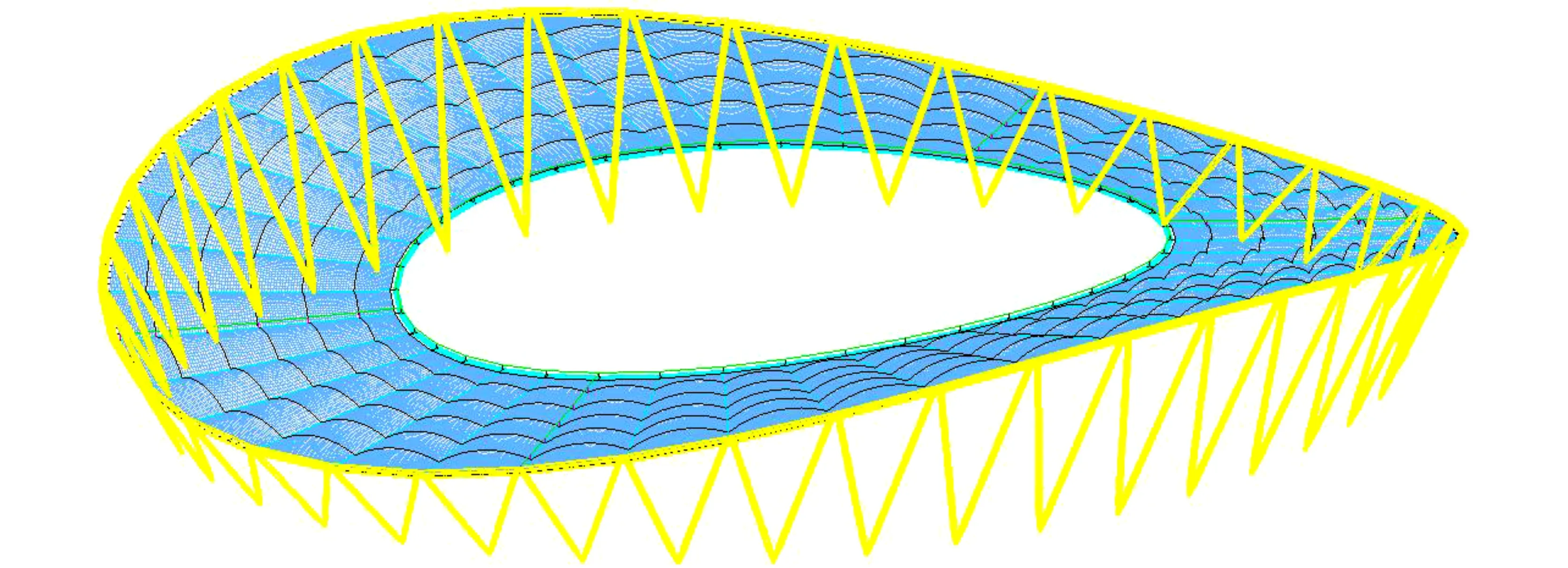
图 1 轮辐式单层索网结构轴测图
1 单层轮辐式索网结构初始形态确定
对于索网结构的初始形状的确定问题,其实质是在索网的几何构形中形成合适的预应力分布使之成为一个自适应平衡体系。单层轮辐式索网结构与索膜结构及正交索网结构不同,通常索网结构的初始形状确定的问题是在给定的边界条件下进行,寻找符合初始态平衡条件的几何形状和与之相对应的预应力分布[8]。
然而,对于单层轮辐式索网结构而言,其初始态几何形状具有一定的独特性。在结构的平面投影和外圈压环的节点坐标确定的条件下,则可以确定唯一的内环索节点坐标,从而确定唯一的单层轮辐式索网结构的空间几何形状。
因此单层轮辐式索网结构在已知支座节点X、Y、Z及内环索节点X、Y坐标的条件下,可合理利用该几何特性,确定其初始状态下的几何位形。该几何特性可被称为“共点三索共平面”原理。
1.1 共点三索共平面确定原理
“共点三索共平面”原理主要利用的是拉索的节点平衡。对于两根共节点的悬索,其索力大小均大于零时,索力可在一维空间平衡,形成一维的索结构(图2a)公式为:
F1+F2=0
(1)
对于三根共节点且不共线的悬索,其索力大小均大于零时,因“共节点的三根索共面”,索力可在二维平面上平衡,形成平面的索结构(图2b),公式为:
(2)
对于共节点且不共面的悬索,其索力均大于零时,索力可在三维空间平衡,形成空间的索结构(图2c),公式为:
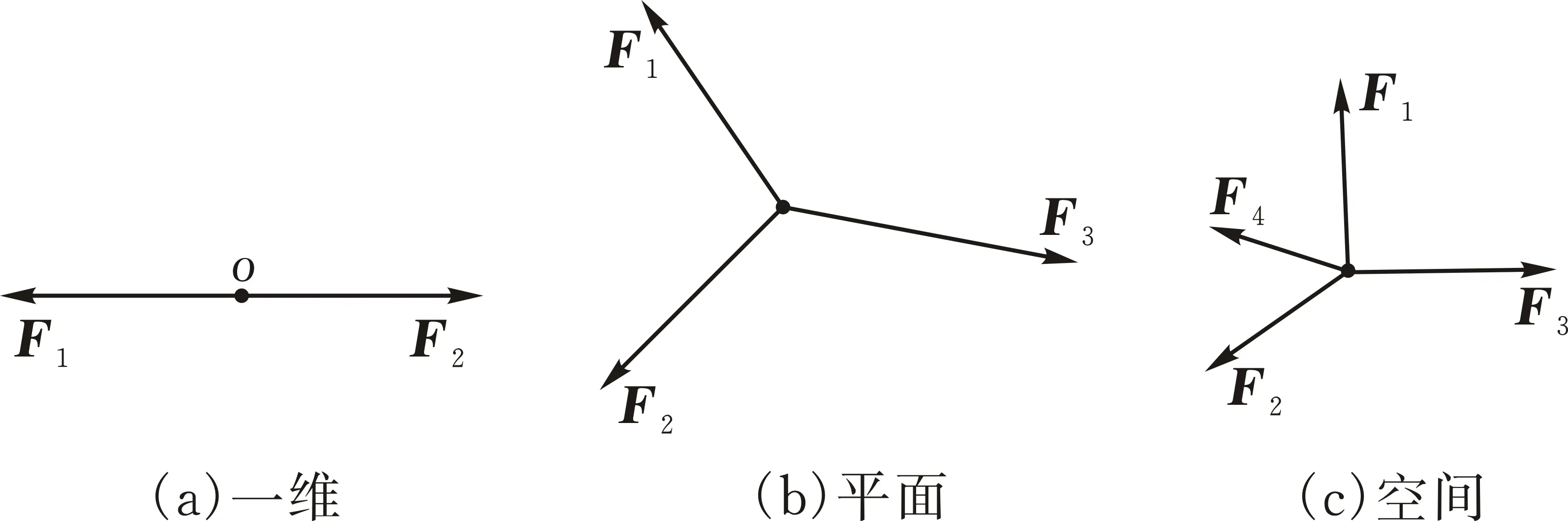
图 2 索结构
(3)
1.2 单层轮辐式初始态几何确定方法
针对本文的研究对象单层轮辐式索网结构(图3),其内环索节点均连接两根环索与一根径向拉索,由“三索共面原理”可知,三根通过环索节点连接的索必定共面。例如,拉索A′B′、BB′、B′C′通过节点B′连接,当拉索BB′、A′B′、B′C′保持张力时,线段BB′、A′B′、B′C′必然在同一平面上,即点A、A′、B′、C′四点共面。
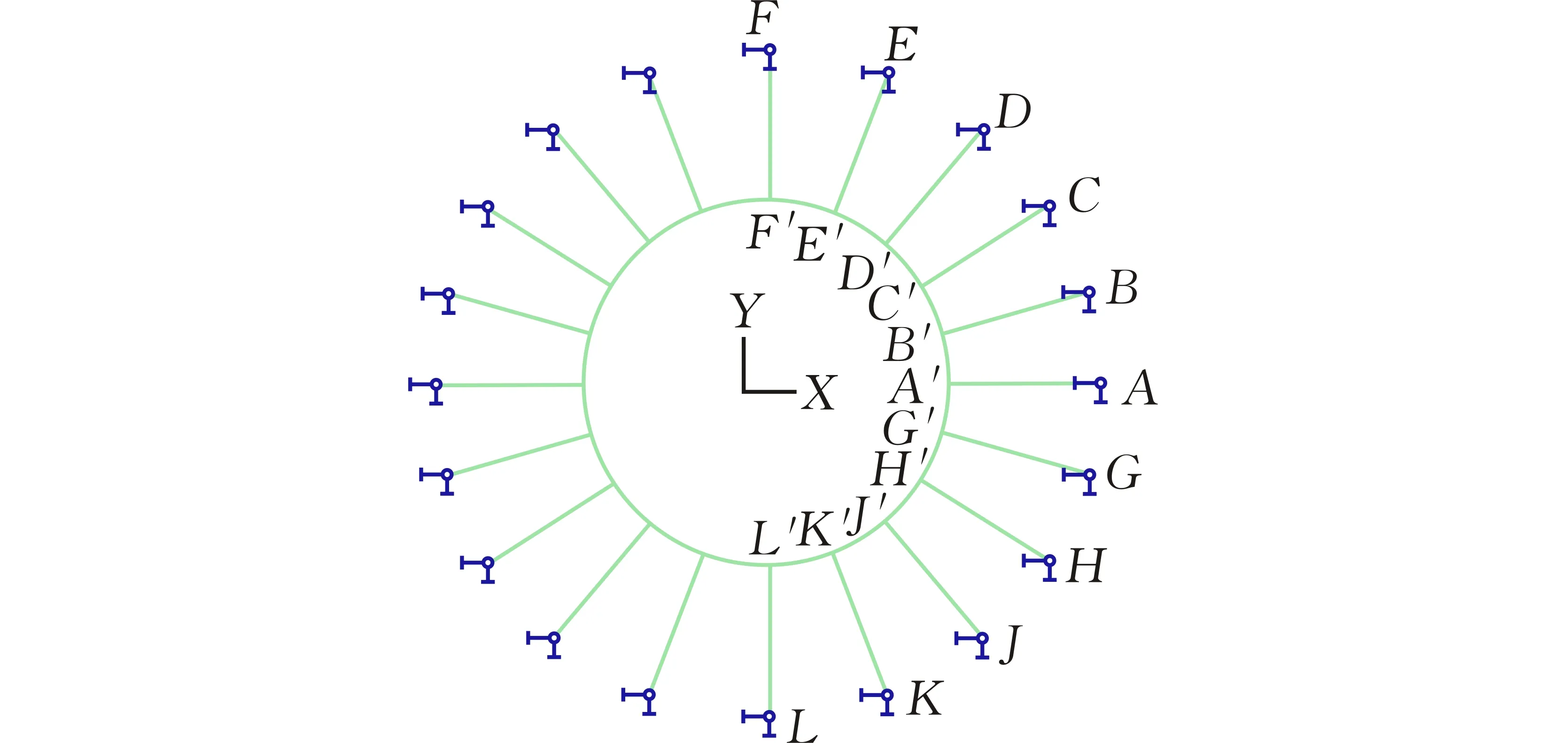
图 3 轮辐式单层索网结构节点示意图
根据“共点三索共平面”原理,在确定平面投影尺寸的情况下通过外圈压环的Z坐标依次确定内圈环索节点的Z坐标,通过迭代循环的方式,最终确定索网的初始几何位形。具体流程如下:
步骤1 确定初始己知量:
1)己知支座节点的X、Y、Z坐标,即XA、YA、ZA、XB、YB、ZB……其中支座A为最高点,支座F为最低点,指定ZF为最低点,指定ZF=0;
2)给定内圈环索节点的X、Y坐标,即XA′、YA′、XB′、YB′……
步骤2 第一次几何位形计算:
1)假定第一次迭代调整因子α1确定ZA′的数值,从而确定ZB′。
假定第一次迭代调整因子α1,其取值范围为(0,1],α1通常取1。定义ZA′=α1ZA,可通过ZA得到ZA′。由于节点B′和节点G关于X轴′对称(图4a),且节点A、A′、B′及G′共面,从而可以确定节点B′和节点G′的初始Z坐标。
2)确定节点C′的初始Z坐标ZC′。
通过步骤2-1可知节点A′、节点B及B′的Z坐标(图4b),由于节点B、A′、B′及C′共面,从而可以确定节点C′的初始Z坐标ZC′。
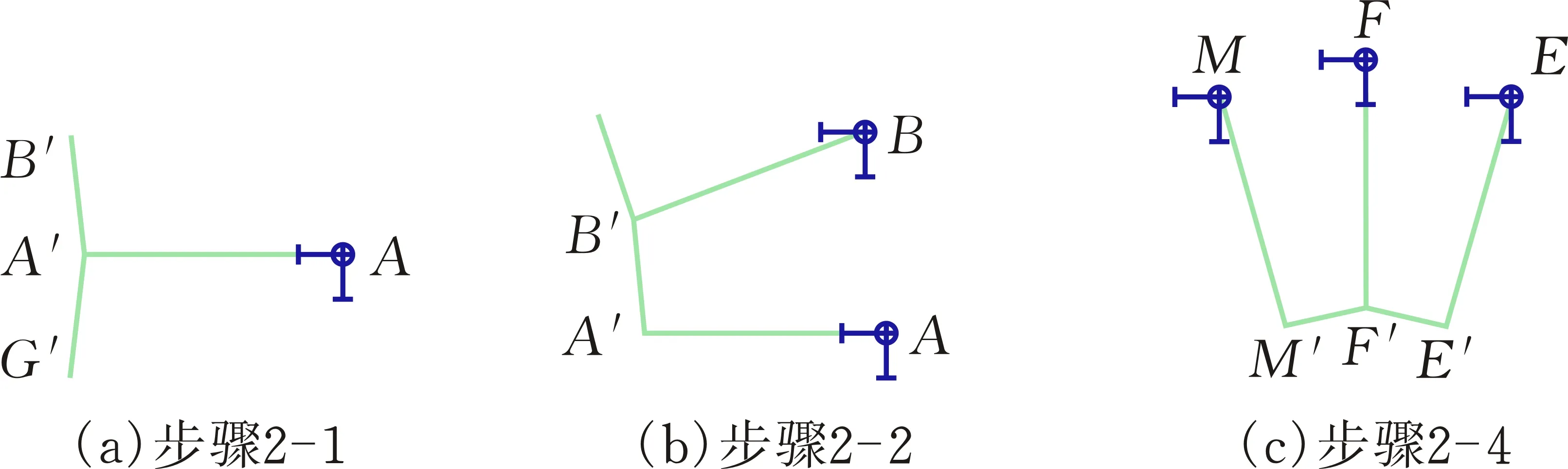
图 4 步骤示意图
3)重复上述操作,确定节点D′、节点E′及F′的Z坐标,得到1/4结构的所有节点坐标。
4)验算节点F坐标误差
由于1/4结构的所有节点坐标均可通过“共点三索共平面”原理确定,节点A到节点E分别在平面B′A′G′,C′B′A′,D′C′B′,E′D′C′及F′E′D′内(图4c)。在此条件下,需验证3)中节点F′坐标误差,以确定节点F′是否在平面E′F′M′内。因节点E′、M′关于Y轴对称,可知两点Z坐标相同,从而得到平面E′F′M′。
设L1为该次支座节点F至E′F′M′的距离,若点F位于平面E′F′M′上方,L取正值,进入步骤3;若点F位于平面E′F′M′下方,L取负值,增大1)中α1取值,重复1),直至L为正。
步骤3 第二次几何位形计算:
假定第二次迭代调整因子α2,其取值范围为(0,1],α2通常取0.05。定义ZA′=α2ZA,其余运算步骤与步骤2中相同。
设L2为该次支座节点F至E′F′M′的距离,若点F位于平面E′F′M′上方,L2取正值,减小α2的取值,重复步骤3,直至L2为负;若点F位于平面E′F′M′下方,进入步骤4。
步骤4 迭代确定点A′的Z坐标:
定义第(i+2)次的调整因子为α3=(α1+α2)/2.其余运算步骤与步骤二中相同。设L3为该次支座节点F至E′F′M′的距离。
若L3小于误差限制值[Um],证明节点位于平面E′F′M′内,满足“共点三索共平面”原理,终止运算;
若L3大于误差限制值[Um]且L3大于零,则调整α1=α3,重复步骤4,直至L3小于限制值[Um];
若L3大于误差限制值[Um]且L3小于零,则调整α2=α3,重复步骤4,直至L3小于限制值[Um];
步骤5 生成完整结构:
由上述操作可得1/4结构的所有节点坐标,根据边界处的对称条件生成完整的结构模型。
1.3 四支座简化算例
本研究通过Grasshopper可视化编程实现迭代流程,针对简化的四支座简化算例进行迭代结果的实现。并与理论解析的四支座简化算例的理论结果进行对比,证明该“单层轮辐式索网结构初始形态方法”的可行性。
本算例为四支座单层轮辐式索网结构,算例计算条件(图5)。

图 5 四支座简化算例示意图
1.3.1算例理论解析该算例结构关于XY轴对称,可知ZA′=ZC′,ZB′=ZD′。
(4)
将节点A、A′坐标代入式(4)中得直线AA′表达方程:
(5)
因直线B′D′与AA′共面,且直线B′D′与Y轴平行,将节点B′坐标代入式(5)中,得B′点坐标表达式:
ZB′=2ZA′-2500
(6)
将节点B、B′坐标代入式(4)中得直线BB′表达方程:
(7)
因直线B′B′与A′C′共面,且直线A′C′与X轴平行,将节点B′坐标代入式(5)中,得A′点坐标表达式,同时联立式(6):
ZA′=1666.67
(8)
最终可得:
(9)
1.3.2初始态几何确定方法实现算例本研究在grasshopper平台中利用可视化编程的方式实现“单层轮辐式索网初始态几何确定方法”对四支座算例进行找形,在本算例中,取第一次迭代调整因子α1=1,第二次迭代调整因子α2=0.05,误差限制值[Um]=0.05,迭代程序如图6所示。

图 6 迭代程序示意图
经过12次迭代,最终得到结果(图7):

图 7 找形结果示意图
(10)
“单层轮辐式索网初始态几何确定方法”实现的四支座算例结果与理论解析计算结果可知,ZA′的误差值为0.0079%,ZB′的误差值为0.0045%,该误差值结果证明“单层轮辐式索网初始态几何确定方法”的可靠性,单层轮辐式索网结构初始态几何可用该方法找形。
2 单层轮辐式索网结构零状态形状确定
单层轮辐式索网结构初始态几何位形可由上节所述“单层轮辐式索网初始态几何确定方法”进行确定,因此单层轮辐式索网结构零状态形状确定的问题属于初始态几何已知问题。针对该类问题目前较为适用的是逆迭代的方法。
2.1 逆迭代基本原理
逆迭代法最开始是用在张弦梁结构的几何形状确定的问题上[9],然后经过发展推广应用在了索网结构找形分析上。逆迭代是基于相似性原理的分析方法,其基本原理为:在给定预应力的条件下,在一次迭代后将所得的节点位移反向作用在初始位形上,更新节点坐标,进行下一次迭代。随着迭代次数的增加,在预应力和自重的作用下结构变形后的位形,该迭代时的几何位形,可被认定为零状态几何[10]。其迭代流程如下:
1)给定索结构的初始态几何X,定义结构的零状态几何X0;
2)给定索的预张力P,初始态几何X在索自重和预张力(通常不平衡)作用下结构产生初始位移d1,结构变形成为X1;
3)将位移d1反向作用于X得到初始迭代几何XK=X-d1;
4)初始迭代几何Xk在索自重和预张力作用下结构产生位移dk,结构变形成为Xk+1;
5)再次将变形dk反向作用于Xk得到迭代几何Xk+2=Xk+1-dk;
6)判断迭代几何Xk+2初始几何X的位移是否小于误差极限值[Dm],若小于误差极限值[Dm],迭代几何Xk+2即为所求零状态几何X0;若大于误差极限值[Dm],则令k=k+2,重新进入步骤4)。
2.2 零状态四支座简化算例
本研究针对2.3节中简化的四支座简化算例(图8)进行相应的零状态找形的研究,通过grasshopper可视化编程实现2.1节所述迭代流程。该算例的弹性模量均为1.6×105N/mm2,拉索强度等级为1670 MPa,径向索BB′设置主动索力F=300 kN。

图 8 零状态四支座简化算例示意图
2.2.1算例理论解析由“共节点三索共平面”原理可知,径向索与两根环索在相连节点处平衡,即:
(11)
由结构关于XY对称可知,FA′B′=FA′D′=FB′C′=FC′D′,代入得:
(12)
由FBB′=300 kN,代入式(12)得:
(13)
2.2.2逆迭代法算例实现根据2.1节中所述逆迭代流程,基于grasshopper参数化设计平台及基于该平台开发的有限元分析插件karamba编制零状态找形程序。因通过误差极限值[Dm]判断逆迭代找形是否成功,在已知预应力分布的条件下,应根据逆迭代求解零状态几何的预应力与已知的预应力进行对比,判断逆迭代法确定零状态是否可行。在该算例中设置最大迭代次数为20次,误差极限值[Dm]=1.0 mm。
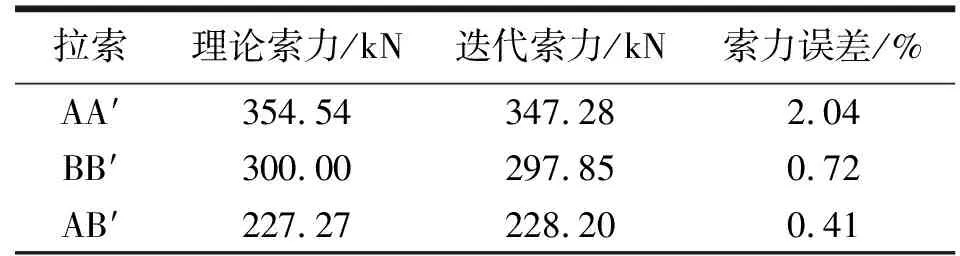
表1 索力对比表
该算例迭代20次后,迭代结束,此时迭代几何X22与初始几何X对比。迭代结果通过对比可知,该算例理论索力与逆迭代索力的索力误差值最大为2.04%,误差在可接受的范围内。并且随着误差极限值[Dm]的减小和迭代次数的增加,计算结果将更为精确。
3 结束语
针对单层轮辐式索网结构初始状态和零状态找形方法进行了系统的研究,并通过参数化平台RHINO和 Grasshopper结合简化算例对找形方法进行验证。研究得出以下结论:
1)针对单层轮辐式索网结构的初始状态几何应根据单层轮辐式索网结构的几何特性进行迭代处理进行几何位形确定;
2)逆迭代法可用于索杆体系的零状态找形问题,同样适用于单层轮辐式索网结构的零状态找形问题;
3)参数化平台RHINO和Grasshopper结合基于该平台的各类插件可实现单层轮辐式索网结构的找形方法。
