低温下混凝土线膨胀系数理论与试验研究

2022-02-28周鹏，李扬，游阳

湖北工业大学学报 2022年1期

周鹏，李扬，游阳

(湖北工业大学土木建筑与环境学院，湖北武汉 430068)

LNG储罐建造、可燃冰开采、寒冷地区房屋建设等。随着混凝土在低温环境下的运用愈加广泛，开展低温下混凝土的相关热力学性能研究具有重大的现实意义。而线膨胀系数表征材料随温度变化的伸缩性能，是影响结构耐久性的重要因素之一。对此，国内外针对线膨胀系数进行了相关研究。

Maruyama[1]通过水浴加热，在60℃内用激光位移计读取混凝土的变形量，确定混凝土的线膨胀系数。Lucie Zuda[2]将试件制作成棒状，采用陶瓷杆引伸法测量试件长度的变化。Siddiqui MS等[3]对不同类型骨料进行研究，发现混凝土的线膨胀系数随所含骨料的线膨胀系数的改变而改变。Yeon J等[4]设置不同湿度的混凝土试件，得出当相对湿度在70%～80%之间时材料线膨胀系数最大，且对材料水泥浆体的影响大于混凝土。芦琴等[5]基于混合率计算材料线膨胀系数，结果表明线膨胀系数值与产生的温度应力大小成正比。

尽管相关研究很多，但大多数实验变温区间较小或直接采用了专业仪器测量。而直接测量极端温度下混凝土线膨胀系数所需仪器成本极高。为探索一种经济适用的研究方法，本文提出了Mori Tanaka方法和电阻应变计法[6]进行线膨胀系数的理论推导和试验研究。

1 实验设计

1.1 试件制作

水泥砂浆试件质量配合比为水泥∶水∶砂=1∶0.4∶1.86，尺寸为100 mm×100 mm×100 mm；石材原料为石灰岩，切割尺寸为100 mm×100 mm×100 mm；混凝土质量配合比水泥∶砂∶石子∶水∶外加剂∶矿粉为1∶2.45∶3.25∶0.45∶0.029∶0.46，骨料级配良好；石英玻璃尺寸为50 mm×50 mm×3 mm。具体测点布置及试件用途如表1所示。

表1 试件详情

1.2 试验过程与方法

1.2.1线膨胀系数测试在混凝土、水泥砂浆、石材及石英玻璃相应位置粘贴尺寸为120 mm×40 mm低温应变片，位置如表1所示。因石英玻璃受温度作用变形极小，故将其作为标准件。同时，额外设置一个混凝土试件，在其中间部位钻孔，埋入PT3W型热电偶，测试试件中心位置温度，以确保所有试件被冻透，达到预定温度。试件测点上的低温应变片采用1/4桥路连接，连接的导线与数据采集仪相连。最后，将试件放入低温试验箱内进行深冷处理。

本试验采用电阻应变计测试方法，设定的标准温度为20℃。通过低温应变片读出试件在低温下的热输出﹐然后根据下式对实验数据进行处理，进而得到试件的线膨胀系数：

α1=α2+(ε1-ε2)/ΔT

(1)

式中：α1为待测试件的线膨胀系数，℃-1；α2为标准件的线膨胀系数，℃-1[7]；ε1为待测试件的热输出；ε2为标准件的热输出；ΔT为温度差值。

1.2.2弹性模量计算在水泥砂浆、石材相应位置粘贴低温应变片，位置如表1所示。同时，设置一个试件，实时测温且不加荷载。试件测点上的应变片均采用1/4桥路与低温导线连接，导线另一端连接采集仪。然后放入低温箱，箱底具有荷载加载装置，对试件进行加荷，如图1所示。

图 1 装置图

结合电阻应变片工作原理，测量不同温度下试件的弹性模量。从常温变温至某一温度Ti时，将加载时实际输出的应变减去该温度下未加载的应变值，此差值正是待测试件在固定荷载作用下引起的应变值，即：

ΔεTi=ε2Ti-ε1Ti=εMTi

(2)

式中：εMTi为Ti温度下的力引起的应变；ε1Ti为Ti温度下未加载时的应变值；ε2Ti为Ti温度下加载时的应变值。

设定试件受力截面面积为A，则在配重荷载N的作用下，温度为Ti时的混凝土弹性模量ETi为

(3)

同理，通过上述方法测出加载与未加载条件下水泥砂浆、石材表面横向与纵向的应变片的应变值，得到不同温度下材料的泊松比，即：

(4)

式中：σTi为Ti温度下材料泊松比；ΔεhTi为Ti温度下横向应变；ΔεzTi为Ti温度下纵向应变。

1.3 试验结果与分析

图2为混凝土、水泥砂浆和石材在低温下各项热力学参数随温度变化曲线。除混凝土线膨胀系数曲线外，水泥砂浆、石材的热力学参数曲线均取三个试件测试值的平均值作图。

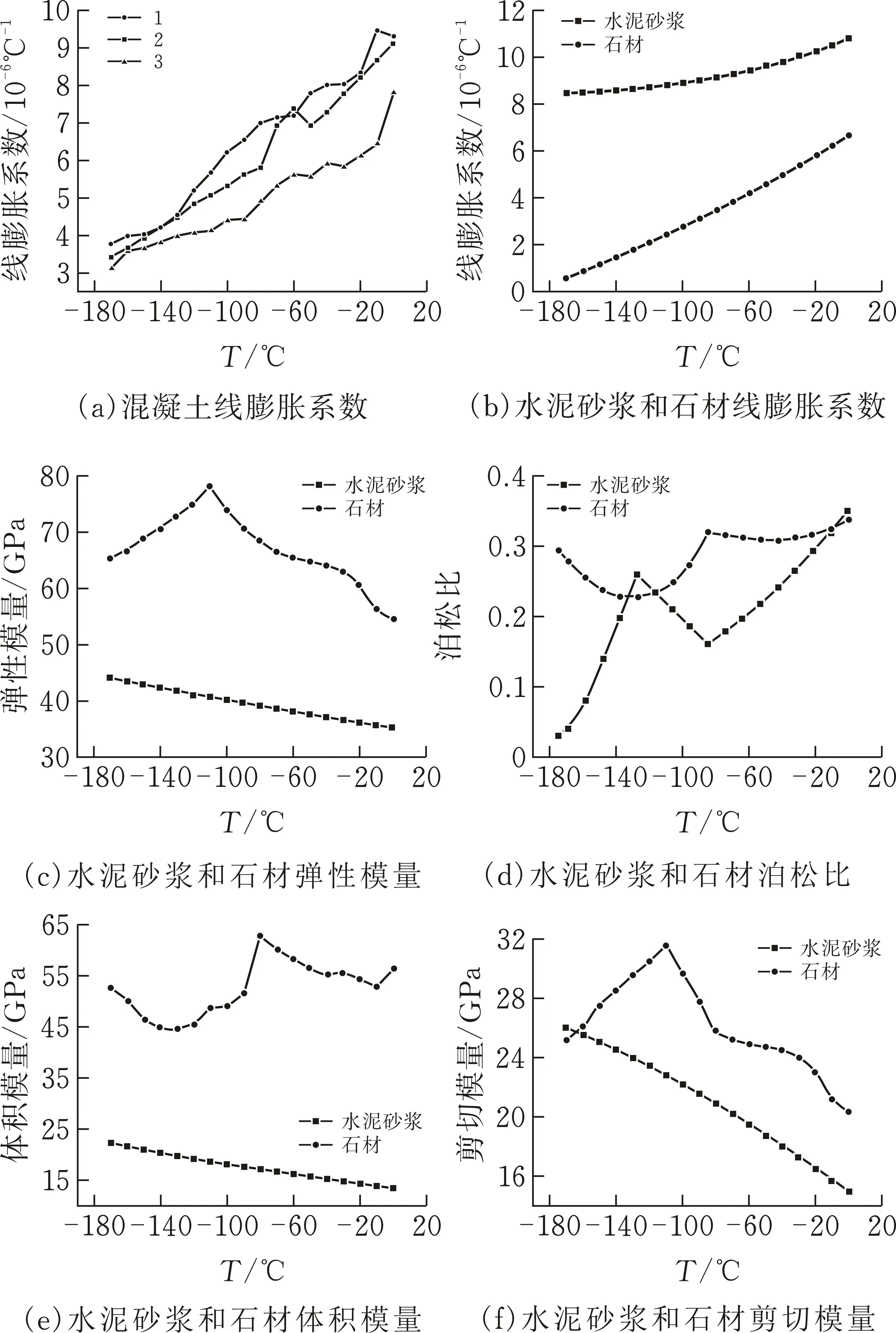
图 2 材料热力学参数曲线

由图2可知：混凝土、水泥砂浆、石材的线膨胀系数基本随温度的下降而降低。在三类材料中，线膨胀系数水泥砂浆大于混凝土大于石灰石。而钱春香[8]的相关研究也证明了这一点；对于弹性模量，由于水泥砂浆和石材孔隙中的水份因温度降低凝结成冰填充了孔隙，提高了材料整体的强度。故其值大体上随着温度的下降而升高。又因水泥砂浆材料本身含水量较石材多，所以强度提高得更明显；对于泊松比，由于低温下孔隙愈加密实、发生变形逐渐困难，因此两种材料相较常温，值都有所下降。

体积模量K用来反映构件的体应变与平均应力之间的关系。其与弹性模量E、泊松比μ之间有关系：

(5)

剪切模量G反映材料在弹性变形范围内，剪切应力与应变的比值。其与弹性模量E、泊松比μ之间有关系：

(6)

将弹性模量与泊松比的值代入上式，得到体积模量与剪切模量的曲线，如图2e、f。

2 理论方法研究混凝土线膨胀系数

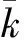
(7)

(8)

式中：γk=(1+ν0)/3(1-ν0)，γμ=(8-10ν0)/15(1-ν0)，ν0表示砂浆的泊松比；μ0和k0，μ1和k1分别表示砂浆和骨料的剪切、体积模量；φ1表示骨料的体积分数。

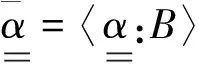
(9)

当混凝土的弹性为各向同性时，可以得到:

(10)

(11)

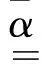
若混凝土线膨胀系数张量为各向同性，则根据式(11)可得:

(12)

其中骨料的体积分数为37%，将上述砂浆和石材热力学参数代入公式中求解，得到混凝土线膨胀系数理论值。经计算，超低温下混凝土各温度点的线膨胀系数理论值与试验值曲线如图3所示。

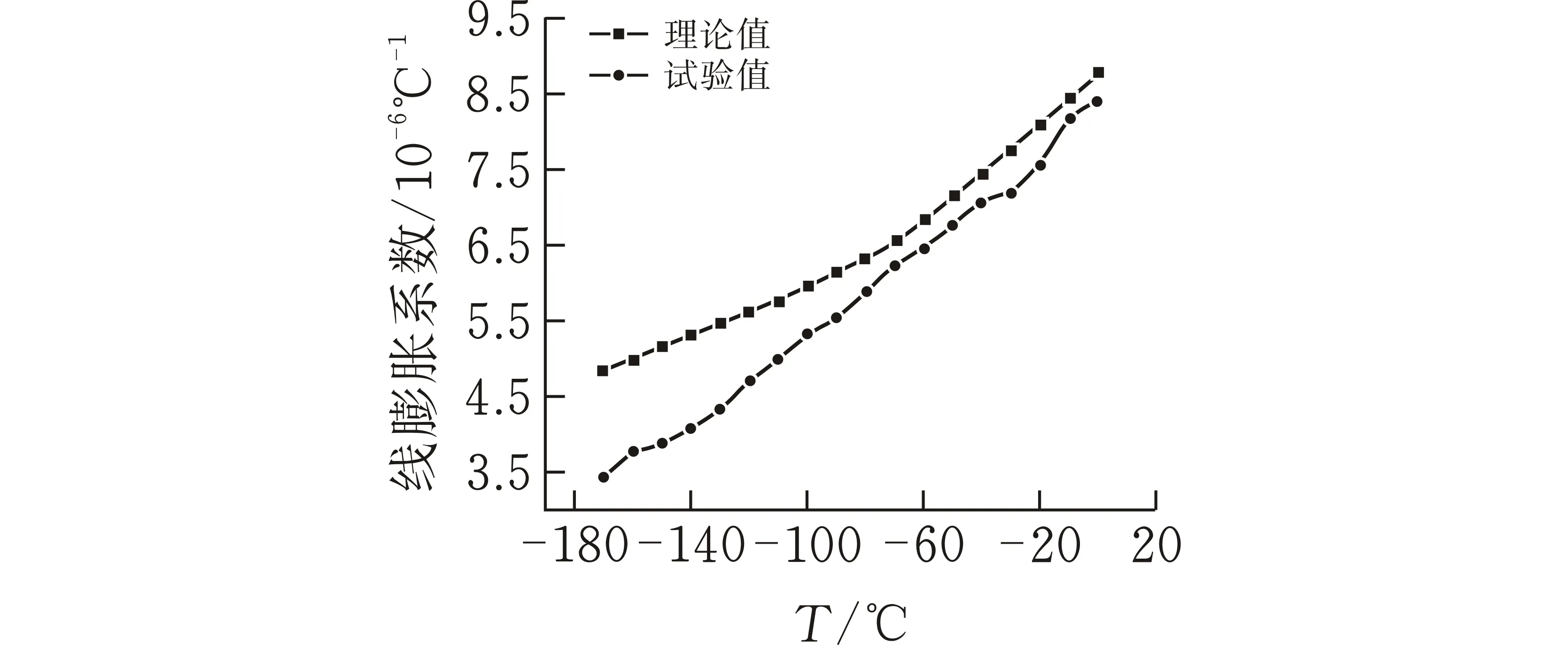
图 3 低温混凝土线膨胀系数理论值与试验值

本文通过试验研究和理论公式推导两种方法，求得混凝土在超低温下的热膨胀系数，由图3可知：试验所得平均线膨胀系数曲线与理论推导线膨胀系数曲线趋势大致相同。随着温度的降低而逐渐下降，与温度基本呈线性关系；理论值曲线较试验值曲线整体更为平缓；在-170℃ 时，二者差值最大，理论值较试验值高出近40%。而在-80℃ 以内，二者相差不超过15%，吻合度较高。

而试验值整体较理论值偏小是因为：在混凝土中，粗骨料自身的强度高于水泥砂浆，其在低温下发生冷缩较水泥砂浆更困难。在水泥砂浆收缩时，粗骨料会抑制水泥砂浆的变形；且在混凝土试件制备过程中，由于粗骨料的加入，配比时会添加一定量的水份。试件水含量的增加导致细小的毛细孔在低温下也完全被冰填充，因此减小了试件的变形。而这一系列的细观反应与理论推理割裂。所以在一定的范围内，理论值与试验值极为接近，但随着温度区间的继续扩大，二者的差值也将随之增大。