函数型Logistic回归模型研究与应用

邓 楠，罗幼喜

(湖北工业大学理学院，湖北 武汉 430068)

随着在许多领域对数据质量的要求都越来越高，对数据的分析也从低频数据分析向高频数据分析进行跨越，但在很多情形，我们获得的数据都为离散的数据，无法完全捕捉数据的信息。基于此，Ramsay于1982年提出了函数型数据分析(FDA)[1]。与传统数据分析相比，FDA具有更多优越性，它通过对数据进行曲线性质的分析进而挖掘出更多重要的信息。在函数型数据分析中，函数型Logistic回归是函数型线性回归模型的一个重要应用。它针对响应变量为二分类数据，协变量为函数型数据建立回归模型，利用样本曲线的信息来预测某件事情发生的可能性，通过函数型变量随时间的变化预测二元响应变量的变化。在国外，Ratcliffe等[2]基于模拟的胎儿心率轨迹构建了函数型Logistic回归模型，将函数协变量和回归函数用傅里叶基函数进行展开，对极大似然估计的计算使用改进的Fisher评分算法，并将此模型应用到胎儿出生风险预测。Kim等[3]考虑若函数数据高度混合，则基于整个区域的分类是无效的，因此提出了基于区间的函数型数据分类方法。该方法利用融合的Lasso惩罚自动选择函数数据中信息最丰富的片段，同时利用函数逻辑回归对选择的片段进行分类。Denhere[4]考虑了当存在异常曲线时对未加处理的数据进行函数型主成分Logistic回归不能得到良好的结果，提出了一种基于稳健主成分的函数型Logistic回归模型。Mousavi等[5]则对许多情况下对函数协变量(作为输入)和二元响应(作为输出)之间的关系感兴趣，由此通过3种方法对该模型的参数估计结果进行比较，并判断这些方法正确分类的能力。在国内，王惠文等[6]针对同时包含数值型多元变量和函数型协变量的广义线性回归模型，采用非参数方法得到了参数部分和非参数部分的估计量，并给出了一种重加权算法进行参数求解，解决了含数值型和函数型混合数据类型自变量的回归问题，由此扩展了函数型线性模型的应用范围。孟银凤等[7]针对传统函数Logistic模型泛化性能不高的问题，通过求解优化问题提出了线性正则化的函数Logistic回归模型。梳理文献发现，尽管已有文献给出了函数型Logistic回归模型的不同分析方法和应用实例，但通过贝叶斯方法对其分类性能的研究还较少。Crainiceanu等[8]曾介绍了在贝叶斯框架下函数型数据的分析方法，使用WinBugs对函数型数据进行分析，但未研究Logistic回归模型的分类性能，Zhu等[9]则提出了针对二元响应变量和多元函数型协变量的贝叶斯变量选择模型，并将其应用于宫颈癌诊断，但其对函数型Logistic回归模型进行Probit变换时，未考虑Logit变换，因此本文考虑在贝叶斯框架下对函数型Logistic回归模型进行Logit变换并对其分类性能进行研究。

1 函数型Logistic回归模型

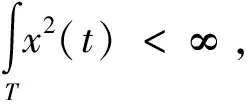
yi=πi+εi,i=1,2,…,N

(1)

其中：

πi=P[Y=1|]xi(t):t∈T}]=

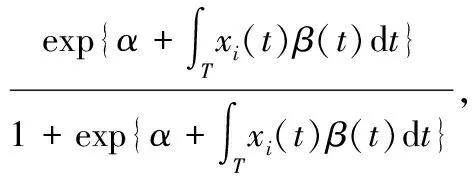
i=1,…,N

(2)

α为实数参数，β(t)为参数函数，εi(i=1,2,…,N)为N个独立且均值为零的随机扰动项。等价地，通过Logit变换，式(2)可以表示为:

i=1,…,N

(3)

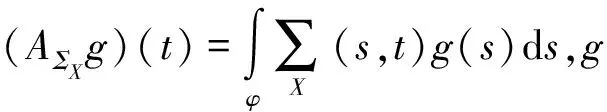
假设选取K个主成分基函数对回归系数函数β(t)和函数数据x(t)进行展开，则

(4)

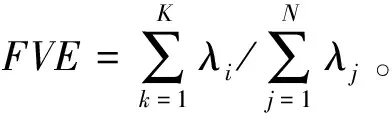
(5)

写成矩阵形式表示为：l=α1+Cb，其中b=(b1,…,bK)T，1=(1,1,…,1)T，C=(cik)N×K为函数主成分得分，其计算方法为：

且满足

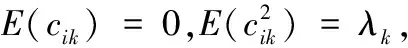
从而在独立条件下，模型的似然函数可以表示为：

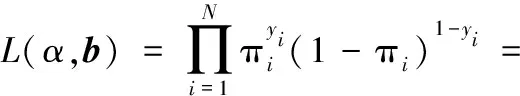
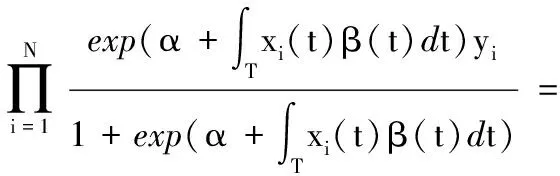
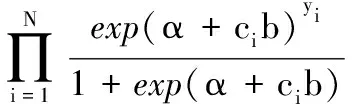
(6)

2 基于Polya-Gamma变换的条件后验分布推导

虽求得函数型Logisic回归模型的似然函数，但由于一般先验和模型似然函数的非共轭性较难求得参数后验，因此考虑通过引入Polson[13]等提出的Polya-Gamma数据增强算法。Polya-Gamma数据增强算法对于不同模型都求得了更简单且有效的后验分布。该数据增强算法表示为：

记ω～PG(b,0),b>0表示服从参数为(b,0)的Polya-Gamma分布，其密度函数

则对于所有a∈R，有下列恒等式成立：

(7)

其中，κ=a-b/2，且p(ω∣ψ)～PG(b,ψ)。该数据增强算法有效规避了常用先验分布与函数型Logistic回归模型似然函数的非共轭性，从而在Polya-Gamma变换下，函数型Logistic回归模型的似然函数可以改写为：

(8)

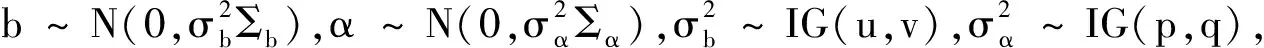
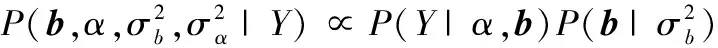
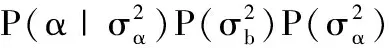
(9)

则b的条件后验可表示为：

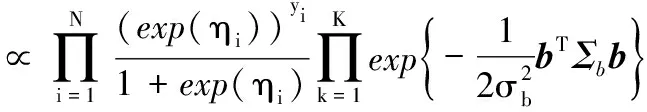
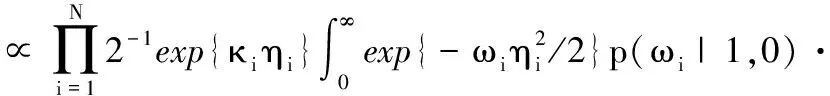
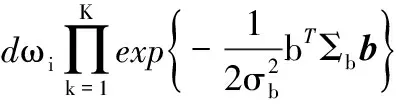
(10)

即b,ω的联合后验为：

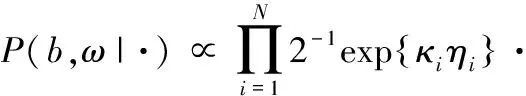
(11)

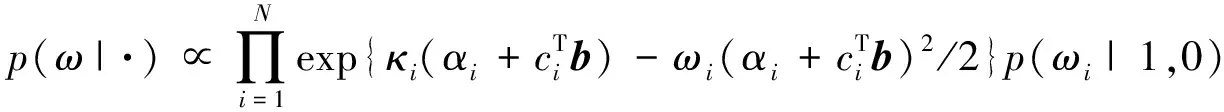
P(ωi|·)=PG(1,ηi)

(12)

由

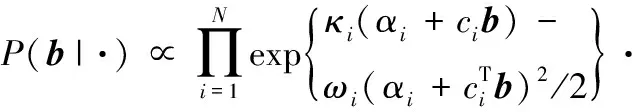
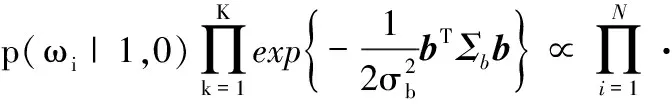
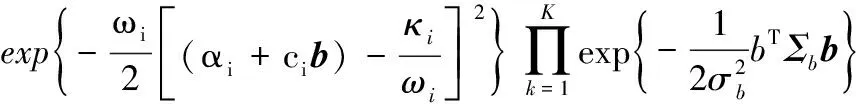
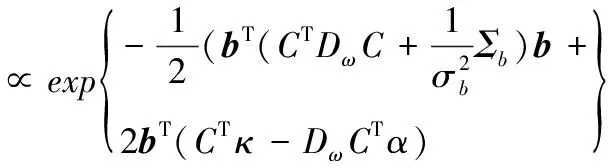
(13)

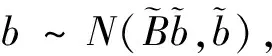
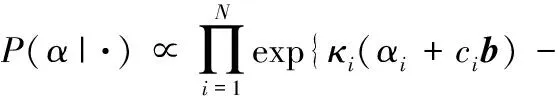
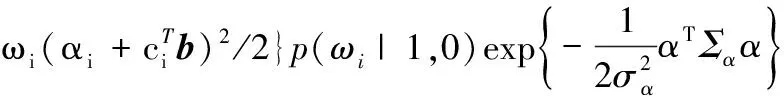
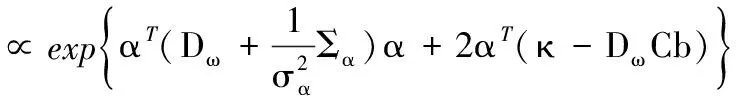
(14)

则α得条件后验为：

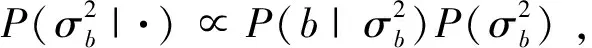
(15)

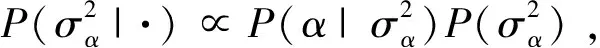
(16)

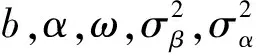
1)ωi|else～PG(1,ηi)，其中ηi=αi+cib；

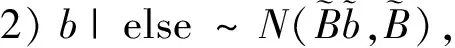
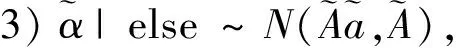
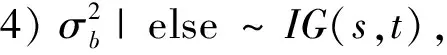
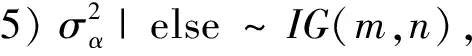
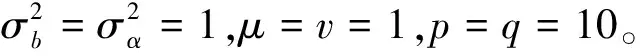
3 数值模拟

3.1 数据生成

首先生成独立同分布的函数型随机变量xi，再根据函数型Logistic回归模型生成响应变量yi。该数据生成方法仿照文献[5]设计，具体数据生成为：

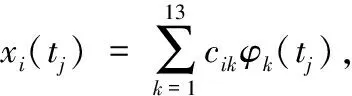
i=1,2,…,150,j=1,2,…,256,tij∈[0,10]

(18)

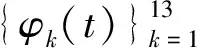
i=1,2,…,150

(19)

其中β(t)为区间T=[0,10]上的已知函数，考虑β1(t)=sin(tπ/3)，β2(t)=-d(t∣2,0.3)+3d(t∣5,0.4)+d(t∣7.5,0.5)，其中d(·∣μ,σ)为服从均值为μ方差为σ的正态分布，采用主成分基函数进行拟合，模拟结果如图1所示。在这里α设为0.5，使用截断点0.5作为分割，即

则Y=1，否则Y=0[14]，图2为参数函数为β1(t)时模拟生成的150条曲线中的40条样本曲线。

图 1 模拟参数函数曲线

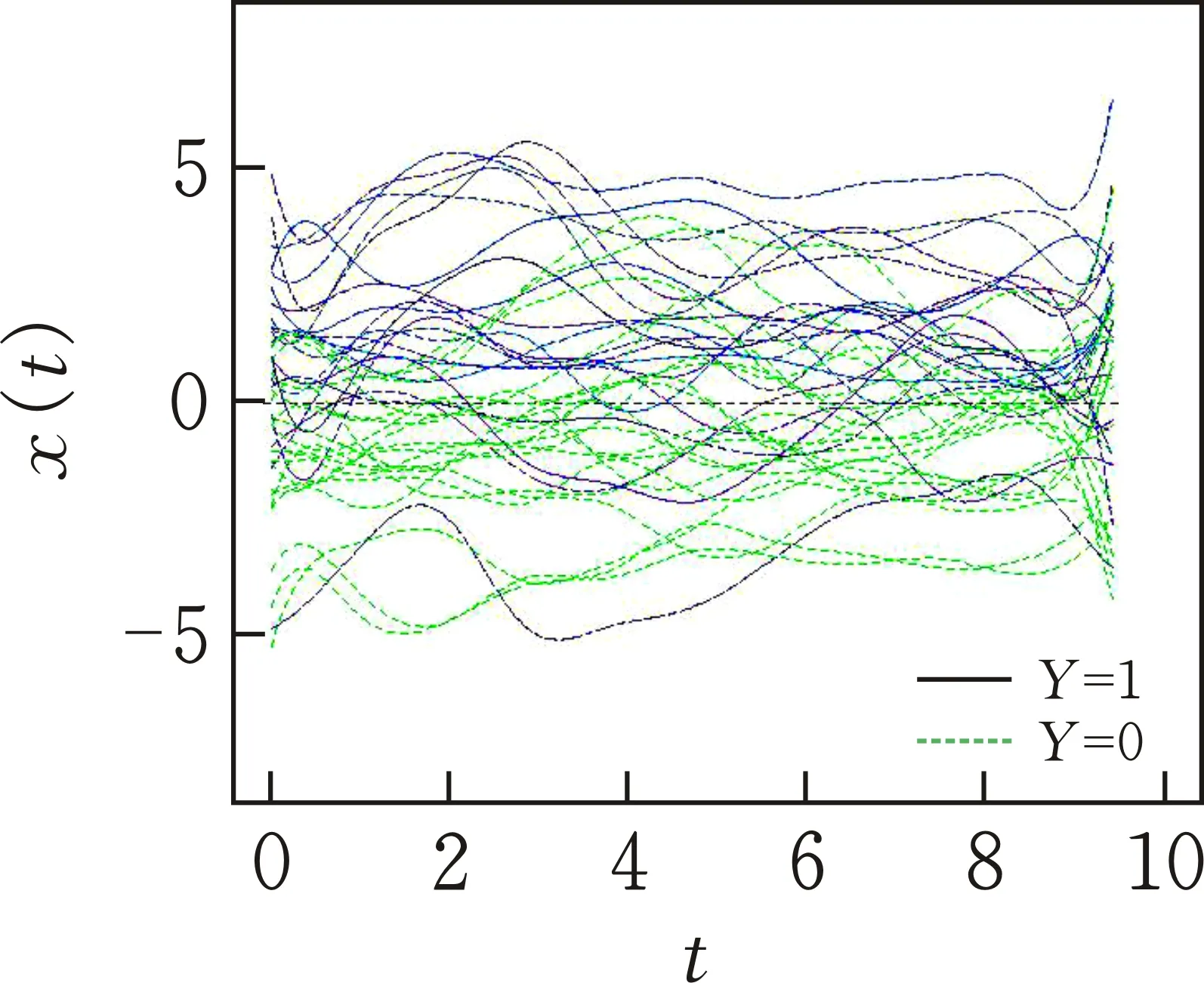
图 2 模拟函数曲线

3.2 模拟结果

为了检验该方法的分类能力，在测量误差分别为0和0.5的情况下对模型进行验证。由于为二分类问题，根据样本的实际标签与分类器给出的预测标签，可将样本分为4种，分别为TruePositive(正类预测为正类的个数为TP)、FalseNegative(正类预测为负类的个数为FN)、FalsePositive(负类预测为正类的个数为FP)、TrueNegative(负类预测为负类的个数为TN)。根据上述定义，可对模拟生成的100个数据集给出4个分类指标，分别是精度(Acc)、准确率(Pre)、召回率(Rec)、F1得分(F1)，其计算公式分别为[7]：

同时将此方法(Bayesian Fuctional Logistic Regression,BFLR)与普通Logistic回归(Logistic Regression,LR)、支持向量机(Support Vector Machine,SVM)、决策树(Decision Tree,DT)、条件推断树(Conditonal Inference Tree,CIT)方法进行比较。

通过对比函数Logistic回归模型与其他分类方法在模拟数据上的分类性能，发现基于BPLR模型的方法对于数据的分类情况明显优于其他方法，在4个分类性能指标上都有更高的准确率。样本路径图、样本密度图和样本自相关函数图表明，在经过预烧期后算法已趋于稳定达到收敛，证明该抽样算法在数据分类上的有效性。

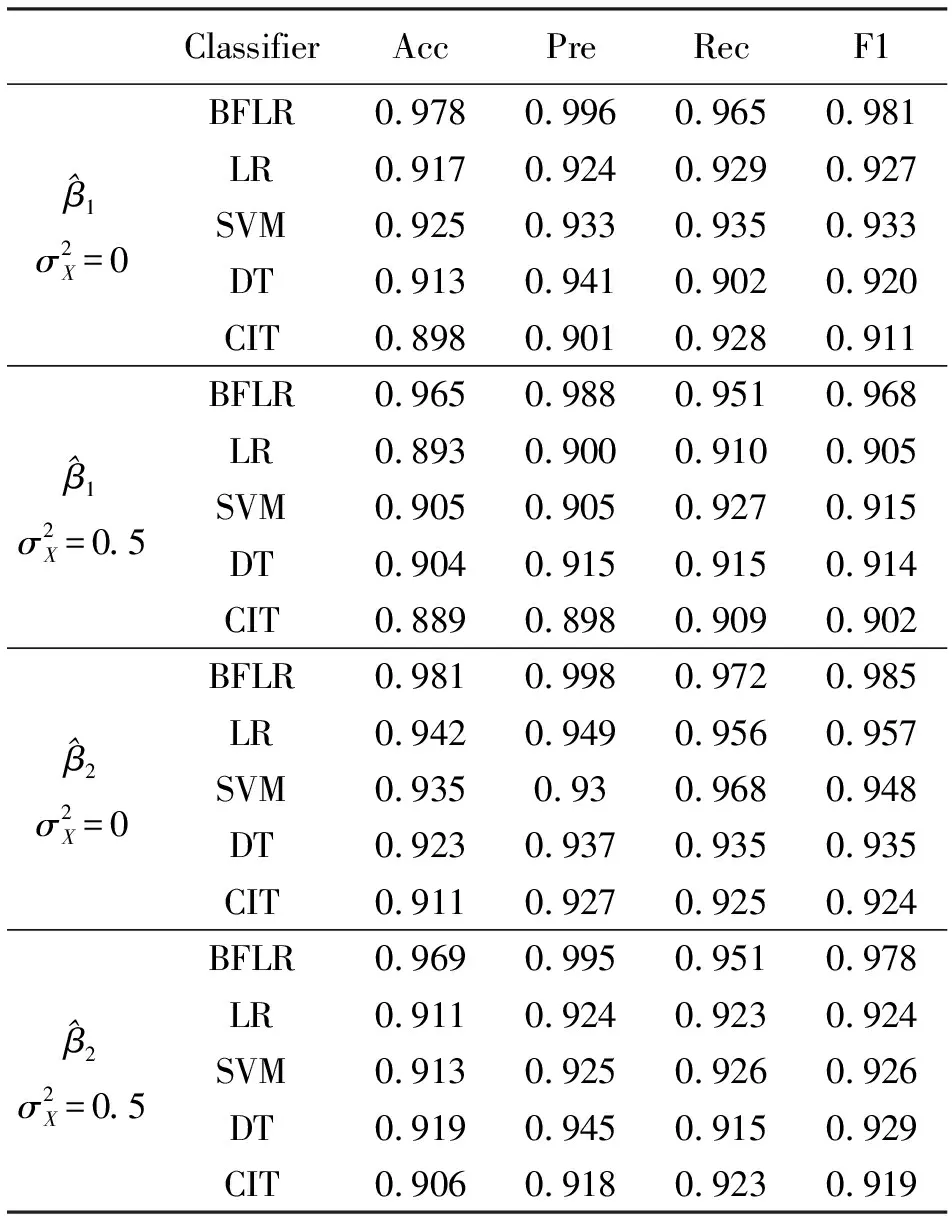
表1 模拟数据分类性能

图 3 N=150，b的样本路径

图 4 N=150，b的样本密度图

图 5 N=150，b的自相关函数

4 实际数据分析

以Tecator数据为例，该数据可在R软件包“fda.usc”[15]中进行下载。Tecator数据集由215个碎肉样本对波长为850～1050 nm的近红外吸收光谱曲线及其脂肪含量构成，每条吸收光谱曲线观测了100个通道，其中有138块碎肉样本的脂肪含量Fat低于20%，77块碎肉样本的脂肪含量Fat高于20%。以此将Tecator数据集分为两类，图6给出了每类的各30条样本曲线。通过函数主成分分析发现T，ecator数据集前3个主成分已经达到99%的累积方差贡献率，因此选取前三个主成分基函数构建函数型Logistic回归模型。该模型可以表示为：

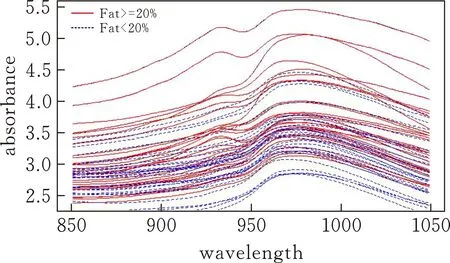
图 6 Tecator数据集

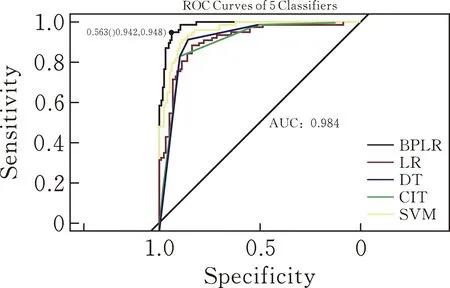
图 7 各分类器ROC曲线

其中初始值α设为0.5，bk=(0,0,0),k=1,2,3，cik为前三个主成分得分。

为检验模型的分类能力，画出模型的ROC曲线。结果显示，基于贝叶斯分析的函数型Logistic回归模型对Tecator数据集的分类效果最优，其AUC面积达到了0.984，说明模型具有较高的分类准确率。与其他方法在4个指标上的分类性能相比，尽管BFLR方法在准确率上表现不如普通Logistic回归、决策树和条件推断树，但在精度、召回率和F1得分上都显著优于其他方法，因此总体来说与其他模型相比拥有更好的分类能力。

表2 Tecator数据集分类性能

5 结束语

本文面向函数型数据的二分类问题，提出一种基于Logit变换的函数型Logistic回归模型，并通过模拟数据和实际数据分析验证了其分类能力。与其他模型的分类性能相比，在该模型上的分类结果均优，但不足是本文考虑的是单变量函数型回归变量的情形，针对多元函数型回归变量以及包括普通数据的函数型Logistic回归模型可为后续研究。