光滑水平圆形管道内两球碰撞的速度规律剖析

洪英兰 王伟民

（1.福建省三明市第二中学，福建 三明 365000；2.安徽省太和县宫集镇中心学校，安徽 太和 236652）

从一道碰撞题目涉及的物理情景说起——

例1.如图1所示，在水平面上固定着一个半径为R的内壁光滑的圆管轨道（R远大于圆管直径）A、B、C、D4个点将圆轨道等分为4等份，在轨道的A点静止放着一个甲球，某一时刻另一个乙球从D点以速度v沿顺时针方向运动，与甲球发生弹性碰撞，小球（可视为质点）直径略小于轨道内径，已知m甲=7m乙，从第1次碰撞开始计数，试确定甲乙两球第2022次碰撞的位置及这次碰撞后两球的速度.

图1

因为管道是水平光滑的，两球发生的是正向完全弹性碰撞，所以，从第1次碰撞开始，在每次碰撞前后，两球组成的系统不仅动量和动能分别守恒，系统的机械能也守恒，因此，无论经过多少次碰撞，一定不存在两球都静止的情况.又因为两球发生弹性碰撞之后，不存在二者等速且同方向运动的情形（只有这样的情形，两球在管道内才不会继续碰撞），所以，两球在水平光滑管道内的碰撞会无止境地进行下去.

题目给出的问题是确定2022次碰撞后两球的速度情况，如果以两球的初始速度为条件，根据弹性碰撞的两球组成系统碰撞前后动量守恒，动能也守恒的规律，可以建立方程组求解第1次碰撞后两球的速度，再以第1次碰撞后两球的速度为条件，用同样的方法可以求解第2次碰撞后两球的速度……，但是，用这样依次递推的方法去求解第2022次碰撞后两球速度的做法显然是不现实的，只有探寻出两球在水平光滑管道内的碰撞运动规律，特别是碰撞过程中两球速度的变换规律，才可以对问题进行求解.

先探讨前面两次碰撞后两球的速度变化规律.

设m乙=m，则m甲=7m，设第1次碰撞之后甲乙两球的速度分别是v1和v2，根据两球在碰撞前后组成系统的动量守恒和动能守恒的规律，可得

显然，第1次碰撞之后，质量大的甲球顺时针方向运动，速度大小是，质量小的乙球以的速度按逆时针方向运动，所以，第2次两球的碰撞点位于B点，如图2所示.设第2次碰撞后甲球和乙球的速度分别是v3和v4，以图2中B点向右的方向为速度的正方向，根据弹性碰撞的规律，

图2

所以，两球第2次碰撞之后，甲球相对管道静止，而乙球以速度v在管道内顺时针方向运动.因此，第3次碰撞的情形跟第1次碰撞时两球的速度情形完全相同，只是碰撞位置不同（第3次碰撞发生在图2中的B点）.

这样看来，光滑水平管道内，初始状况以速度v顺时针方向运动的乙球与静止的甲球发生正向完全弹性碰撞，之后的无数次碰撞是有规律的，如果从第1次碰撞开始进行碰撞次数计数的话，那么，两个球在管道内的运动规律是，第奇数次撞击后，甲球在水平光滑圆形管道内以的速度按顺时针方向运动，乙球以3倍甲球的速度按逆时针方向运动，乙球运行管道长度之后，发生与其碰撞次数序号相邻的第偶数次碰撞，而每个偶数次碰撞之后，甲球相对管道保持静止，乙球以原来的初始速度大小沿顺时针方向去撞击它.这种撞击运动将永不停息、周而复始的循环下去.如果以两次碰撞为一个碰撞循环的话，那么，在每个碰撞循环内，甲球在水平光滑管道内按顺时针方向运动管道长度，因此，如果从第一次撞击开始计数，那么，第8k次和8k+1（k为非负整数）次撞击位置位于图1中的A点.

由于2022=8×252+6，所以，第2022次碰撞发生在图1中的D点，这次碰撞之后，甲球速度为零，乙球以速度v在管道内顺时针方向运动.

因为两个物体发生完全弹性碰撞的过程，在任意惯性参考系内动量和动能都分别守恒，所以，对于上述问题甲乙两球第2次碰撞后速度的求解，无需再一次建立方程组进行解答（解二元方程组的过程是一个相对比较麻烦的过程），变换惯性参考系之后根据速度的相对性原理和弹性碰撞的规律，即可方便快捷地确定二次碰撞之后甲乙两球的速度.

如图2所示，两球第2次碰撞时，在临近碰撞前的瞬间，它们的相对速度为v，这就是说，如果以甲球为参照物，那么，乙球在临近撞击前的运动速度为v，因此，如果在两球碰撞时，选择图2中相对水平管道向右以的速度匀速运动的空间为参考系（惯性参考系），则在此参考系中，甲球静止不动，乙球以大小为v的速度按逆时针方向与甲发生正向完全弹性碰撞，这与例题1给出的两球初始运动情形变得完全一样了，区别仅仅是撞击的方向和两球在轨道内的撞击位置不同，因为在新的惯性参考系中，两球碰撞过程中它们组成系统的动能和动量也都分别守恒，所以，两球第2次碰撞之后，于新参考系中甲球在图2的B位置以的速度逆时针运动，乙球以的速度顺时针方向运动，因此，相对于原参考系（即相对水平管道），甲球保持静止，乙球以速度v顺时针方向运动，所以，两次撞击之后，在要发生第3次撞击之前，这种运动规律又“退回”到例题1初始的物理情景，区别是质量大的甲球不是静止于水平管道的A点去“等待”质量小的乙球以速度v按顺时针方向去撞击它，而是质量大的甲球静止于管道的B点“静候”乙的撞击，撞击的方向和速度都没有发生变化.

显然，对于例1给出的问题，两球速度的这种周期性变换规律是一种非常奇妙的规律，我们不禁要问，这种看似神奇的撞击运动规律原因何在？题目给出两球质量关系等式m甲=7m乙中的倍数7如果发生变化，对两球撞击之后速度变化规律有什么影响呢？

我们看下如果将题目中的质量关系条件m甲=7m乙，式中的质量倍数7更改为任意正实数之后，两球的碰撞规律是怎样的情形.

设m甲=km乙（k是任意正实数），碰撞之后甲乙两球的速度分别为v1和v2，设m乙=m，则m甲=km，由碰撞前后系统的动量守恒和动能守恒可得

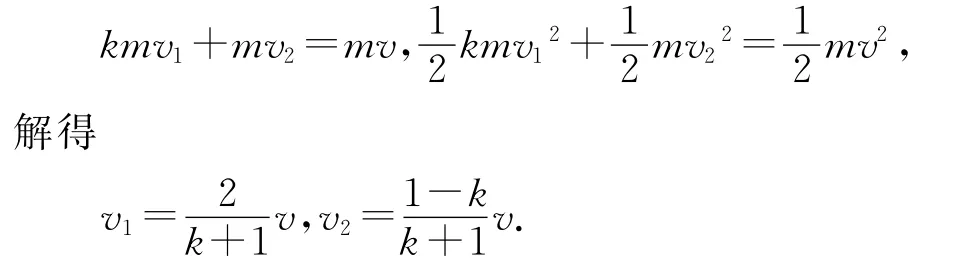
下面按k的大小分类讨论两球碰撞时速度的变化规律.

当k=1时，v1=v，v2=0，这刚好是质量相等的两球发生正向完全弹性碰撞后，两球彼此交换速度的情形（这也间接说明我们推理结果的正确性）.这种情况下两球碰撞的规律是——如图1所示，乙球在A点以速度v按顺时针方向撞击甲球（第1次碰撞）之后，乙球静止，甲球则以速度v在管道内顺时针方向匀速转动，运动一周之后与乙球碰撞（第2次碰撞），彼此交换速度之后，甲球静止，乙球以速度v在管道内沿顺时针方向匀速运动，这便回到了两球的初始运动状态，两球会按这一碰撞规律不停的在管道内运动下去.

当k＞1时，v1＞0，v2＜0，两球碰撞之后，质量大的甲球以的速度在管道内顺时针方向运动，质量小的乙球以的速度在管道内逆时针方向运动，发生第2次碰撞时，相对甲球，乙的速度依然为原来的速度v，所以，第2次碰撞的过程，如果选择在碰撞位置以的速度（这恰好是第2次碰撞前甲球相对管道的速度）相对轨道匀速运动的空间为参考系（新的惯性参考系），那么，在新的参考系中，甲球是静止的，乙球在以速度v按逆时针方向撞击甲球，由于第2次撞击之时，在新参考系中，两球组成系统的动能守恒，动量也守恒，所以，根据两球碰撞建立的求解碰撞之后两球速度的方程组，跟第1次碰撞在原参考系中建立的方程组形式完全相同，不用说方程组的解也相同，因此，新参考系中第2次撞击之后甲球以的速度逆时针运动，乙球以的速度顺时针运动，所以，相对原来的参考系，第2次撞击之后，甲球相对水平管道静止，而乙球则以大小为v的速度沿顺时针方向运动，接下来的第3次撞击过程将变得跟第1次撞击没有差别，不同之处仅仅是它们在管道内撞击的位置不同.

当k＜1时，v1＞0，v2＞0，两球第1次碰撞之后都在管道内沿顺时针方向运动，只不过质量小的甲球运动速度大，质量大的乙球运动速度小，碰撞之后它们相对管道的速度分别为，当甲球比乙球多运动1圈要发生第2次碰撞时，以相对甲球保持静止的空间为参考系（即在碰撞点沿甲球的运动方向以的速度匀速运动的空间为参考系），则乙球在管道内以速度v按逆时针方向去撞击静止的甲球，在新参考系（惯性参考系）中两球撞击前后系统动能和动量分别守恒，因此，第2次碰撞之后，相对新参考系，甲乙两球都在管道内逆时针方向运动，质量小的甲球运动较快，速度是，质量大的乙球运动较慢，速度为，所以，相对于原参考系（即相对于管道），甲球是静止的，而乙球是按顺时针方向运动，相对管道的速度是v，这又回到了初始的碰撞情形，不同点是两球在圆形轨道内碰撞的位置不同.

所以，如果两球质量相等，那么，包括两球第1次碰撞在内的所有碰撞，都发生在管道中的同一位置（即图1中的A点），每撞击两次后两球的速度分别回复到它们的初始速度.在两球质量不等的情况下，如果从第1次撞击开始计数，那么，相对于水平管道，两球在管道内撞击运动的速度规律是，第奇数次撞击后，甲球以的速度顺时针方向运动，乙球以的速度逆时针方向运动（k＞1时），或者以的速度顺时针方向运动（k＜1时），第偶数次撞击之后，甲球静止，乙球以速度v在管道内顺时针方向运动.按这一规律，甲乙两球会周而复始，循环不断的在管道内不停的撞击运动.

对于k＞1的情形，因为第奇数次撞击之后，两球运动方向相反，甲乙两球的速度比是，所以，在第奇数次撞击和邻近的下次偶数次撞击之间的时间段内，质量大的甲球在管道内运动了整个圆形管道周长的，k=7时，，这刚好是例题1题目条件下第奇数次撞击和邻近偶数次撞击之间甲球在管道内运动的距离.

这样看来，水平光滑管道内，运动的小球乙以一定的速度去撞击静止的小球甲，如果两球发生的是正向完全弹性碰撞，不论两球质量比大小如何，若从第1次撞击开始计数，那么，两个小球运动速度的变化规律是以连续撞击两次为一个循环周期，所有的第奇数次撞击都与第一次撞击时两球的速度情形相同——都是甲球静止，乙球以固定的初始速度按第一次的绕行方向去撞击静止的甲球.

以上我们分析的物理情境，是光滑水平管道内运动的小球去撞击静止小球之后，两球在管道内的运动碰撞规律.那么，对于初始情形下两球都是运动的状况，它们在水平光滑圆形管道内撞击之后的运动规律也可以确定吗？

答案是肯定的.

若初始状况下甲、乙两球分别以速度v1和速度v2在管道内运动，在它们第1次撞击时，以相对甲球静止的空间为参考系（惯性参考系），则甲球静止，乙球以v1+v2的相对速度（两球运动反向时）或以｜v1-v2｜的相对速度（两球运动同向，且速度值不等时）去撞击静止的甲球，因为变换惯性参考系之后，两球撞击的过程中系统动能和机械能都分别守恒，所以，在新的惯性参考系中，两球从第1次撞击之后的运动规律，跟我们上面分析的相对原参考系第1次撞击之后两球的运动规律是一样的，都是经历两次碰撞完成一个循环周期，第偶数次碰撞之后，甲球静止，乙球以固定的速度去撞击静止的甲球.因此，再退回到原来的参考系（即以水平光滑圆形管道为参考系）之后，两球撞击过程速度的变化规律是，从第1次撞击开始计数，之后，每奇数次撞击前（也是每偶数次撞击之后），甲乙两球运动的速度情形与初始状况运动的速度大小和方向都分别相同.