从2020年高考谈气体问题备考建议

蔡本再

（复旦大学附属中学青浦分校，上海 201799）

热学知识是高中物理体系中不可或缺的部分，是学生从分子角度认识物理世界的一个重要载体，为学生联系物理微观世界和宏观世界提供了基础.高考中经常以热学知识为背景，通过解决气体问题，考查学生物理观念、科学思维、科学探究等素养.

1 2020高考热学考察总体情况分析

在2020年全国各地的高考试卷中，有6份试卷中考查了热学问题.对比分析6份试卷中热学部分问题的题型、分值、试题背景、知识点和考查的素养，如表1所示.

表1 2020年全国高考气体问题对比分析

从选择性上看，山东卷和天津卷中，热学问题为必考题；全国Ⅰ卷、Ⅱ卷、Ⅲ卷、和江苏卷中热学作为选择性试题，学生可在选修3-3和选修3-4两个模块任选一个作答.从分值上看，热学部分分值总体上差不多，大约占总卷分值的10%左右.从题型上看，除天津卷外，其余都是以计算题为主.从试题的命制看，热学部分试题考查的重点落在一定质量的理想气体的动态过程分析，考查学生结合热力学第一定律、气体实验定律或理想气体状态方程分析气体变化的过程；试题基本上不是以简单的物理模型直接出现，而是普遍具备一定的生活实际和科学技术背景，比如山东卷的“中医拔火罐”、全国Ⅱ卷的“潜水钟”、天津卷的“水枪”，既考查学生的建模能力、用物理知识解决生活实际问题能力，又落实了学生的物理观念和科学思维等素养的考查.

2 2020高考部分热学试题赏析

例1.（2020山东卷12）一定质量的理想气体从状态a开始，经a→b、b→c、c→a3个过程后回到初始状态a，其p-V图像如图1所示.已知3个状态的坐标分别为a（V0，2p0）、b（2V0，p0）、c（3V0，2p0），以下判断正确的是

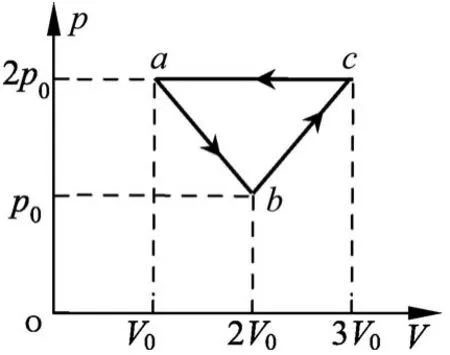
图1

（A）气体在a→b过程中对外界做的功小于在b→c过程中对外界做的功.

（B）气体在a→b过程中从外界吸收的热量大于在b→c过程中从外界吸收的热量.

（C）在c→a过程中，外界对气体做的功小于气体向外界放出的热量.

（D）气体在c→a过程中内能的减少量大于b→c过程中内能的增加量.

本题以描述气体状态变化的p-V图像为背景，考查学生应用理想气体状态方程和热力学第一定律.想要求解该问题，学生的总体思路如图2所示，先借助气体p-V图像中的体积变化确定气体对外界做功还是外界对气体做功，再根据“面积”确定功的大小；利用理想气体状态方程确定3个状态的温度大小关系，从而确定3个过程的内能变化情况；最后根据热力学第一定律确定各过程是吸热还是放热，并对比吸放热的多少.

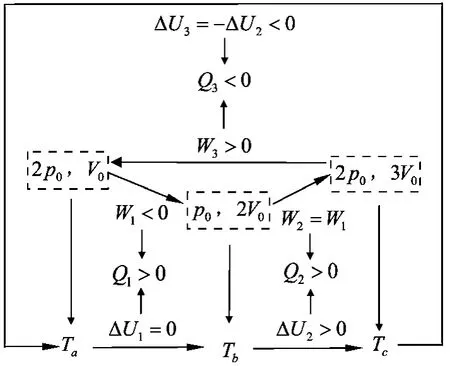
图2 例1求解思路

例2.（2020年全国Ⅰ卷）甲、乙两个储气罐储存有同种气体（可视为理想气体）.甲罐的容积为V，罐中气体的压强为p；乙罐的容积为2V，罐中气体的压强为现通过连接两罐的细管把甲罐中的部分气体调配到乙罐中去，两罐中气体温度相同且在调配过程中保持不变，调配后两罐中气体的压强相等.求调配后：

（1）两罐中气体的压强；

（2）甲罐中气体的质量与甲罐中原有气体的质量之比.

该题第（1）小题求将同一温度、不同压强、不同体积的两罐气体连通后的混合气体压强.第（2）小题求解同一温度、不同体积、不同压强的同种气体质量比值.两个过程均不符合气体实验定律中“一定质量的气体”的前提，属于“变质量问题”.需将变质量气体转换为定质量气体求解.求解思路如图3，先将乙罐气体等温压缩至压强为p的状态，然后将其与相同温度、不同压强的甲罐气体联通，压强不变.然后再改变联通气体体积等于直接联通时的体积，就可以求出压强.第二问需要将甲罐中的气体还原成压强p的状态，利用相同温度、相同压强下密度相同的特点，可得质量比就等于体积反比.

图3 例2求解思路

解析：（1）假设将乙罐中的气体等温压缩至p，体积变为V′，根据玻意耳定律有

将压缩后的乙罐气体与甲罐联通，压强都是p，体积为（V+V′），将调配后的两罐气体膨胀为两罐原体积之和（V+2V），压强为p′.

根据玻意尔定律

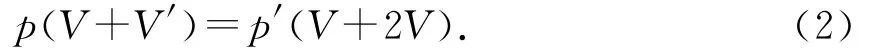
联立（1）、（2）式可得

（2）若调配后将甲气体再等温压缩到气体原来的压强为p，则

由密度定义可得，质量之比

该题也可以用克拉珀龙方程求解.

3 高考气体问题备考策略

3.1 分层次理解气体压强的微观解释

要让学生理解气体分子对器壁的撞击使气体对器壁产生了压强，引导学生从宏观和微观两个方面理解影响气体压强的因素.宏观上气体压强与单位体积内的分子数、气体的温度有关；微观上与分子的密集程度、热运动的激烈程度有关.可根据学生的认知情况分两个层次理解微观上的影响.① 假设Δp为分子在Δt内与容器壁碰撞时动量变化量的平均值，据动量定理有F·Δt=Δp；若N为时间Δt内与器壁面积ΔS碰撞的分子数，则压强.由该式可知当气体体积减小时，分子密集程度变大，N变大，压强增大；若温度升高，分子热运动剧烈，Δp与N都变大，从而压强增大（如图4）；②若根据，将上式进一步推导，可得（n为单位体积内的分子数）.则可知，若温度升高分子平均动能增加，压强增大；若体积减小，则分子数密度增大（如图4）.

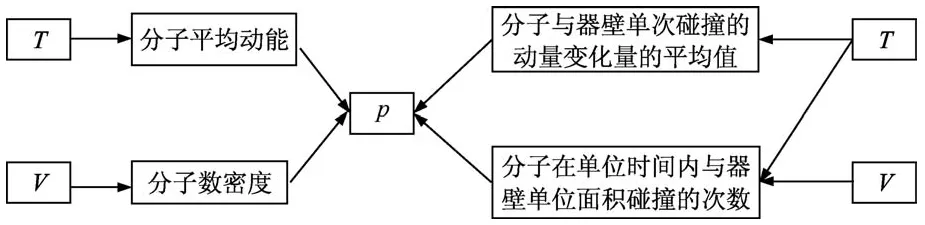
图4 气体压强的微观解释

3.2 多渠道理顺各物理量之间的关系

热学知识包含的物理量较多，涉及它们之间关系的规律主要有理想气体状态方程、热力学第一定律（ΔU=Q+W）、内能的定义.教师需教会学生打通这些物理量之间的相互联系（如图5所示）.除了由3条方程明确它们之间的关系外，还隐含着如下关系：①气体体积V的变化与外界对气体做功的正负相联系.气体体积减小，外界对气体做功，W为正；气体体积增大时，气体对外界做功，W为负（当气体向真空膨胀时为特例，W为0）；② 气体体积与气体分子势能的关系.如果是理想气体，则不考虑分子势能；若为一般的气体，分子力体现为引力，体积变大（减小），分子势能增加（减小）；③ 温度T与分子平均动能的联系.温度升高（降低），分子平均动能增加（减少）；④ 内能增加（减少），ΔU为正（负）.

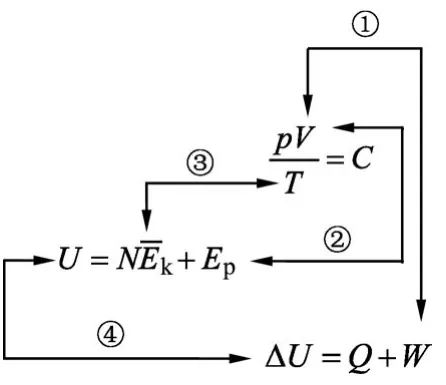
图5 热力学各物理量之间的联系

学生可根据图5关系建立气体变化过程的物理量之间的联系.例如判断一定质量的理想气体经历等压压缩过程是否吸热，可遵循如下思路：因气体压缩（V变小），说明外界对气体做功，即W＞0；同时又因为等压变化，由理想气体状态方程可知温度降低，内能减小，即ΔU＜0；再由热力学第一定律ΔU=Q+W，可知Q＜0，所以气体在该过程中放热.

3.3 多种方法处理气体的“变质量”问题

气体中的“变质量”问题，主要包含两种情形：一是将相同种类、不同状态（压强或温度）的气体甲和乙连通或混合到一定体积的容器内，比如用打气筒将一定质量的气体充入轮胎；二是将一定质量的气体分成不同状态（压强或温度）的几部分气体，比如将高压氧气瓶的气体充入不同的容器.

对比常见两种情境下两种方法的求解思路（如表2所示），借助克拉珀龙方程求解“变质量”问题，先列出混合前后处于同一状态的气体的方程，然后找到各部分气体物质的量之间的数学关系，联立方程便可求解.该方法物理思想较为简单，但并不在高中物理教材之中，未接触克拉珀龙方程的学生往往借助理想气体状态方程求解.

表2 两种典型变质量问题的分析思路对比

用理想气体状态方程求解时，学生需要明确以下两个推论.推论1：相同温度、相同压强的不同体积的同种气体，质量之比等于体积之比.推论2：若将相同温度、相同压强的不同体积的同种气体相互连通（总体积不变），则连通后的气体温度和压强不变.以上两个推论可以借助压强微观解释来推导，也可以借助克拉珀龙方程推导.

用理想气体状态方程求解变质量问题，先要选择合适的研究对象，保证在变化过程的初、末状态气体总质量不变，即将“变质量”转化为“定质量”；然后借助于以上两个推论，列方程求解，有时可根据问题需要创设虚拟变化过程，分阶段列理想气体状态方程.