利用径向有效势能的性质巧解竞赛题

郑 金

（凌源市职教中心，辽宁 凌源 122500）

1 归纳径向有效势能的性质

对于质点在有心力作用下的曲线运动，在极坐标系中的总能量为，由于质点的角动量守恒，则J=mvθr保持不变，因此总能量为

因此可把第2项与第3项之和称为径向运动的“有效势能”，即为

当径向动能为0时，有效势能取最大值，即Ueff=E.此时质点径向速度为0，恰好到达径向运动的转折点，那么质点到力心的距离为最大值或最小值.当质点到达径向运动的平衡点时，有效势能取最小值.

有效势能的公式、有效势能的取值范围、有效势能的极值条件以及有效势能在平衡点关于矢径的二阶导数的物理含义，实际都物理学中的二级结论，在用来解答有关的物理问题时无形地省略了某些推导过程，由此可起到化繁为简的作用.

2 利用有效势能的性质解题

对于质点在有心力作用下的某些物理问题，可利用有效势能的表达式把复杂的二维运动问题转化为一维运动问题来解决，这种方法独特新颖，简便快捷.下面以3道物理竞赛题为例进行分析.

例1.（第26届决赛题第3题）如图1所示，在水平面上有两根垂直相交的内壁光滑的连通细管，管内放置两个质量均为m、电荷量均为q的同号带电质点A和B.开始时，质点A至两管交点O的距离为d，质点B位于交点O处，速度相互垂直，方向如图1所示，大小均为，k为静电力常量.求在以后的运动过程中，它们之间的最小距离.

图1

解法1：利用机械能守恒定律和角动量守恒定律.

首先分析某时刻质点A和B在平面内的受力情况如图2所示，利用正交分解法可知，对于质点A有Fsinθ=NA，对于质点B有Fsinθ=maB.

图2

若以质点B为参考系，则质点A受到的惯性力大小为F′=maB，其方向与NA方向相反.由此可知，此惯性力恰好与轨道弹力NA相互抵消，那么质点A的运动相当于在有心场中的运动，则相对于质点B既有纵向运动，又有横向运动即转动.

质点A相对于B的初速度大小为，方向斜向下，沿第4象限的角平分线方向.在有心力的作用下，角动量保持不变，可知质点A相对于B的角动量大小为

质点A相对于B的总能量保持不变，即为

有心力为库仑斥力，相对初速度方向与斥力方向夹角为钝角，瞄准距离大于0，类似于α粒子散射，因此质点A相对于B的运动轨迹为双曲线，质点B位于焦点，可知当质点A运动到轨迹的顶点时二者之间的距离最小，且相对速度方向与矢径垂直，设此时相对速度大小为v，两个质点之间的距离为r，由角动量守恒定律有

联立方程可得4r2-2dr-d2=0，

点评：解题关键是选择其中一个质点为参考系，对另一个质点考虑惯性力，使其只受到有心力的作用，并且需计算初始角动量和总能量.在应用角动量守恒定律列方程时，需首先判断运动轨迹为双曲线，以便确定质点运动至轨迹顶点时到力心的距离最小；在列角动量守恒方程以及能量守恒方程时，需选择两个特殊点，而且涉及到的速度都用相对于参考点的速度，通过联立两个方程来求出距离的最小值.

解法2：利用径向有效势能的取值范围.

设某时刻质点A到B的距离为r，在转动参考系中，质点A的有效势能为

点评：除了选择质点B为平动参考系外，还需选择极径为转动参考系，以便写出质点的有效势能，并且根据“有效势能不大于总能量”求出距离的最小值.若不用抛物线分析距离的最小值，则可对不等式进行观察，可知r存在最小值，当Ueff=E时r取最小值，则有方程

例2.在真空中有两个质点的质量分别为m和M，带电荷量分别为+q1和-q2，开始相距为l，其中质点M的初速度为0，质点m的初速度大小为v，方向垂直于二者的连线，已知两个质点的距离存在最小值，不计万有引力，求它们在以后运动过程中距离的最小值.

解法1：利用等效势能和机械能守恒定律.

开始时质点M的加速度大小为，

方向由质点M指向m.

若以质点M为参考系，则质点m受到惯性力的大小为F′=maM，方向由质点m指向M.设距离变量为r，则质点m受到的合力的大小为

方向由质点m指向M.

由此可见，质点m受到有心力的作用，由于初速度方向与作用力方向垂直，而且两个质点的距离存在最小值，因此质点m相对于质点M做椭圆运动.取无穷远处的电势能为零，设椭圆轨道的半长轴为a，与卫星的机械能总量表达式进行类比，可知质点m在椭圆轨道上运动的总能量为

点评：之所以没有利用角动量守恒定律列方程，是因为在应用机械能守恒定律列方程时，利用了椭圆运动的总能量公式.但卫星做椭圆运动的机械能总量公式成立的条件是中心天体的质量比环绕天体的质量大得多，即在卫星的质量比地球的质量小得多的条件下，方可认为地球固定不动.对于题中的两个带电质点而言，没有给出质量相差悬殊这个条件，若认为其中一个质点固定不动，则需对另一个质点添加惯性力，或者认为其折合质量为，那么系统的能量守恒方程应为

解法2：利用径向有效势能的取值范围.

当径向动能为0时，有效势能等于总能量，即

刚开始运动时，质点的相对初速度方向与矢径垂直，由于质点相对运动的角动量守恒，可知J=m′vl.

考虑到椭圆运动的总能量小于0，可得关于r的一元二次方程

方程的两个根分别为距离的最大值和最小值，可知二者之和等于椭圆的长轴，即

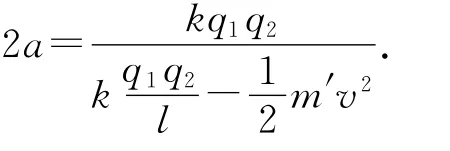
利用求根公式可知

由此可得距离的最大值为r1=l，最小值为

点评：解题关键是利用径向运动转折点的特点列方程，即当径向动能为零时，有效势能等于总能量，通过解方程可求得质点到力心距离的最大值或最小值.要特别注意有关方程中的质量是指折合质量.

例3.如图3所示，两个同轴带电无限长半圆柱面，内外圆柱面半径分别为a、b，设在a＜r＜b区域内只有径向电场，已知场强分布为，电势分布为，其中k和b为常量.现有质量为m、带电荷量为-q（q＞0）的粒子组成的粒子束以大小相同的初速度v0从左方射入，不计电荷间的相互作用，其中初速度的方向既与圆柱面轴线垂直又与入射处直径垂直的粒子刚好沿半径为R（a＜R＜b）的半圆轨道运动.（1）试求v0的值；（2）若其他粒子的入射方向与半圆轨道的切线偏离一个很小的角度β，粒子将偏离半圆轨道，设新轨道与半圆轨道相交于图中的P点.试证明：对于很小的β角，粒子束可以在P点准确聚焦，其位置与β无关，并求出P点的方位角∠AOP的数值.

图3

（2）粒子只受径向电场力的作用，对O点的力矩为0，因此粒子在运动过程中角动量守恒，即

J=mv0R=mr2ω，

在非匀速转动参考系中，以无穷远处为势能零点，可知有效势能为

有效势能关于矢径的一阶导数为

在r=R处，关于矢径的二阶导数为

表明带电粒子在r=R处时处于稳定平衡状态.由于β很小，则粒子偏离平衡位置的距离很小，因此径向运动是简谐运动.可知等效劲度系数为，所以径向运动周期为

利用简谐运动的对称性可知，粒子从初始位置运动到交点P经历的时间为半个周期，即

所以P点的方位角即粒子横向转过的角度为

点评：由于其他粒子的入射方向与半圆轨道的切线偏离一个很小的角度β，则粒子运动轨迹将偏离半圆轨道，那么曲线运动不是匀速转动，角速度将发生变化，但由于粒子只受到有心力的作用，则角动量守恒，因此可利用有效势能公式进行解答.径向运动具有对称性，由于是小振动，则属于简谐运动的一部分，相继两次经过径向运动平衡位置的时间恰好等于半个周期.

综上可见，对于质点在有心力作用下的曲线运动问题，除了一般解法外，有时还可利用有效势能的性质进行解答，不仅拓展了解题思路和方法，还可化繁为简，显得巧妙快捷.