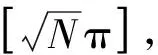碰撞出来的圆周率
——两球与墙壁三者间的碰撞次数与圆周率π间关系的讨论
2020-06-07陈怡
陈 怡
(浙江金华第一中学,浙江 金华 321015)
1 问题的提出
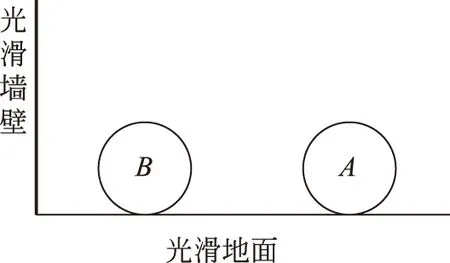
图1
如图1所示,左侧为光滑墙壁,下方为可向右侧无限延伸的光滑地面。A、B两球大小相等,置于地面上,现给A向左的初速度。假设球与球,球与墙壁之间的碰撞为均无动能损失。如果A、B两球质量相等,A碰上B,A停下来B继续运动,B碰到墙后再返回与A相碰,球与球、球与墙之间一共发生了3次碰撞。如果球A的质量大于B,那么A碰完B之后,A还会继续向墙运动,总共的碰撞次数可能会大于3次。实际上:当A的质量是B的一万倍时,共碰撞314次。当A的质量是B的一百万倍时,共碰撞3141次。当A的质量是B的一亿倍时,共碰撞31415次。很明显地发现,总的碰撞次数会与圆周率的数值有关,那么为何两球与墙壁三者间的总碰撞次数会与圆周率联系在一起?
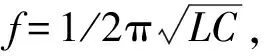
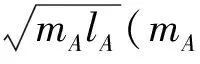
本文立足于两个小球在碰撞过程中速度变换关系而完全舍弃位置参量来解决A,B两球与墙壁三者间的总碰撞次数和圆周率的关系问题,采用碰撞过程中的速度变换关系的证明方法可以直接构造出平面直角坐标系下的圆方程,进而利用碰撞前后在单位圆圆周上的变换关系直接得到最后的结论,整个讨论过程物理意义明确,几何关系简单。
2 分析与论证
为简单起见作如下假设:如图2所示,A球质量为mA=Nm,B球质量为mB=m,规定向左为正方向,初始时A球具有向左的初速度v0。
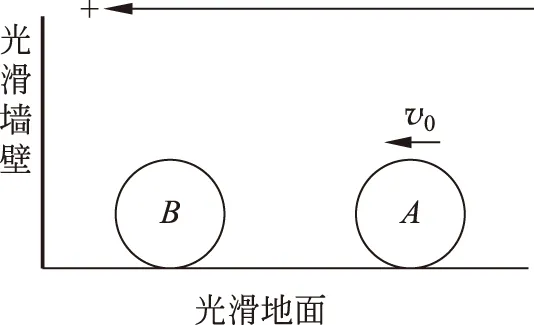
图2
2.1 A,B两球和墙壁三者之间任一次碰撞中的能量动量关系
设某时刻,A,B两球发生第n次碰撞,那么从一开始到第n次两球碰撞的时间间隔内,B球与墙壁共发生了n-1次碰撞。设A,B两球第n次碰撞之后瞬间的速率分别为vAn,vBn,由于B球与墙壁之间的碰撞只能使得B球的运动方向反向,而不改变B球的运动速率,故A,B两球第n次碰撞之前瞬间的速率也就是A,B两球第n-1次碰撞之后瞬间的速率vAn-1,vBn-1。A,B两球第1次碰撞之前的速率分别为vA0=v0,vB0=0。
A,B两球发生第n次碰撞前后满足动量守恒定律,故而有
(1)
由于A,B两球之间的碰撞是完全弹性碰撞,总动能保持不变。由于墙壁保持不动,B球与墙壁之间的碰撞虽然不满足动量守恒定律,但是B球与墙壁之间碰撞前后无动能损失,B球动能保持不变。因此在A,B两球与墙壁三者的碰撞过程中,总动能保持不变,可得
(2)
联立(1)和(2)两式可以解得,
(3)
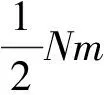
(4)

(5)
也就意味着,A,B两球任意一次碰撞前后的速率可用平面直角坐标系上单位圆上的点来描述,进而可设
将(6)和(7)两式代入式(1),化简后可得
(8)
因而得到
(9)
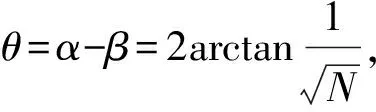

图3
A,B两球第一次碰撞之前,A球和B球速率分别为
(10)
即为单位圆上的点(1,0)。
A,B两球第一次碰撞之后,根据式(3)可得,A球和B球速率分别为
(11)
因此在第一次碰撞前后,在单位圆上逆时针转过的角度为
(12)
依次类推,A,B两球第n次碰撞之后瞬间的速度为
(13)
即在图3的单位圆上以横轴正方向为基准逆时针转过角度nθ。
2.2 A,B两球和墙壁三者间结束碰撞的条件
假定A,B两球经过k次碰撞后,两者彻底结束碰撞,以后两球不再碰撞。考察整个碰撞过程中B与墙壁的碰撞次数。若要求A,B两球终结碰撞,此后不再碰撞,有以下两种可能的方式:
第一种终结碰撞的方式是A,B两球经过k-1次碰撞后,A球向右运动,B球向左运动,B球与墙壁碰撞后向右运动并追上向右运动的A球,进行第k次碰撞,碰后A,B两球均向右运动,但B球的速率小于A球速率。即要求
vAk<0,vBk<0且|vAk|≥|vBk|
(14)
A,B之间碰撞k次,B与墙壁碰撞k-1次,共碰撞2k-1次。
第二种终结碰撞的方式是A,B两球经过k次碰撞后,A球向右运动,B球向左运动,B球与墙壁碰撞后虽然向右运动但已经追不上向右运动的A球。即要求
vAk<0,vBk>0且|vAk|≥|vBk|
(15)
A,B之间碰撞k次,B与墙壁碰撞k次,共碰撞2k次。
2.3 A,B两球和墙壁三者间的总碰撞次数
若以第一种方式终结碰撞,要求
(16)
且
(17)
联立式(16)和(17)可得kθ应位于第三象限,即要求
(18)
再结合式(12),可得
(19)
A,B及墙壁之间的总碰撞次数满足如下条件
(20)
即总碰撞次数为
(21)
其中[]表示取整,很显然总碰撞次数与圆周率有关。当N很大时,根据近似公式
(22)
可将式(21)化为

(23)
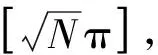
若以第二种方式终结碰撞,要求
(24)
且
(25)
联立(16)和(17)两式可得kθ应位于第二象限,即要求
(26)
再结合式(12),可得
(27)
A,B及墙壁之间的总碰撞次数满足如下条件
(28)
即总碰撞次数为
(29)
其中[]表示取整,很显然总碰撞次数与圆周率有关。当N很大时,根据近似公式
(30)
可将式(29)化为
(31)
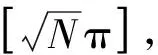
3 结论与启示