单摆球在横向有心力作用下的稳定条件分析——兼谈2021年上海市高考选择性考试物理卷第17题成立的条件

张怀华

（焦作市第十一中学，河南 焦作 454000）

1 引言

共点力作用下物体的平衡条件、万有引力定律、单摆振动规律、数学近似运算和物理学史均为高中物理教学的重要内容，亦是高考命题的热点.2021年上海市高考选择性考试物理卷第17题就是一道将上述知识点相互渗透、有机融合的创新型试题.

例题.（2021年上海市高考选择性考试物理卷第17题）测量引力常量G的实验装置如图1所示，小球（可视为质点）处于静止状态，摆线偏离竖直方向一个小角度θ0，两球心之间的距离为r.当质量为M的均匀圆球突然快速移开后，小球的运动________（填写“可以”或“不可以”）视为简谐运动.若测出两球心距r0、圆球质量M、小球偏离竖直方向的水平距离d和小球摆动的周期T，则引力常量G可以表示为________.（当θ0很小时，sinθ0≈tanθ0）

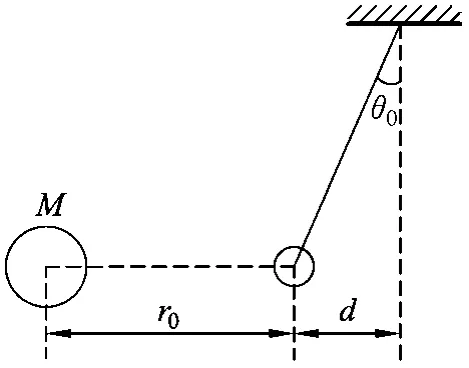
图1

该题的物理情景十分新颖，考查的范围也比较全面，侧重于对学生模型建构和推理分析等高阶思维品质的考查，综合性较强，难度偏大.

笔者带领学生们对该题进行深入分析和研究后发现，单摆球在如图1所示的位置有可能处于不稳平衡状态，从而在微扰作用下失去稳定.为了确保试题命制的科学性，必须附加r0＞2d的限制条件.

2 单摆球在横向有心力作用下的稳定条件分析

大量的文献资料显示，物体在遵循平方反比规律的有心引力和线性弹簧的共同作用下，物体处于稳定平衡状态的条件十分苛刻，稍有不慎，物体就会失去平衡.［1-6］因此，很多相似的实际问题都是建立在单摆球在横向有心斥力作用下保持稳定的情形下的.［7-8］

鉴于2021年上海高考选择性考试物理卷第17题的物理情景是单摆球在横向万有引力作用下的平衡，而单摆球在小摆角条件下的摆线拉力的水平分力与偏移量成正比，则单摆球在横向有心引力作用下处于稳定平衡状态的条件十分苛刻，极易在微扰作用下失去平衡.

2.1 单摆球在横向引力作用下的稳定条件分析

如图2所示，如果单摆球在大质量球M的引力作用下向左偏θ0角后保持静止状态，则由能量最低原理可知，单摆球在左偏角θ0位置的总势能Ep必须具有极小值.［10，11］

图2

为了确保单摆球在左偏角θ0位置处的总势能具有最小值，就必须寻找总势能Ep与左偏角θ的函数关系.

2.1.1 单摆球总势能与左偏角的关系式

由力的平衡条件可得

由三角知识可知，单摆球的摆线长度为

若设单摆球向左偏离竖直方向的角度为θ，则单摆球与大质量球M的距离为

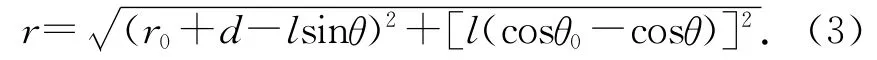
由万有引力势能公式可知［12，13］

这里以无穷远处为引力势能零点.

由（1）-（4）式可得

单摆球具有的引力势能为

以摆球最低点为重力势能零点.

由（2）、（6）式可得

由（5）、（7）式可得，单摆球具有的总势能为

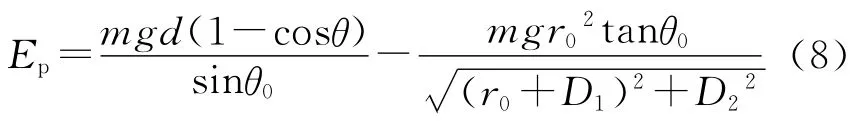
2.1.2 单摆球在左偏角θ0位置处的平衡类型分析

若单摆球在左偏角θ0位置处于稳定平衡状态，其总势能Ep对左偏角θ在左偏角θ0位置的一阶导数必须等于0，同时二阶导数必须大于0.

对（8）式在左偏角θ0位置求一阶导数，可得

对（8）式在左偏角θ0位置求二阶导数，可得

令（10）式大于0，可得单摆球在左偏角θ0位置处于稳定平衡状态的条件为

若令左偏角θ0→0，则（11）式可简化为

在几何画板软件中分别绘制（8）式在r0＞2d和r0＜2d条件下的函数图像如图3和图4所示.

图3 r0＞2d

图4 r0＜2d

对比图3和（9）、（11）、（12）式可以发现，当单摆球与大质量球之间的距离r0＞2d时，单摆球在θ0位置的总势能存在如图3所示的极小值，可以在如图1所示的左偏角θ0位置处于稳定平衡状态.

对比图4和（9）、（11）、（12）式可以发现，当单摆球与大质量球之间的距离r0＜2d时，单摆球在θ0位置的总势能存在如图4所示的极大值，无法在如图1所示的左偏角θ0位置处于稳定平衡状态.

2.2 单摆球在横向引力作用下的稳定条件分析

既然单摆球在如图1所示的有心引力作用下在左偏角θ0处可能失稳，那么单摆球能否在如图5所示的有心斥力作用下在右偏角θ0处保持稳定呢？

图5

为了分析单摆球在右偏角θ0处的平衡类型，不妨设单摆球向右偏离最低点的角度为θ，则由勾股定理可得，单摆球与点电荷M的距离为

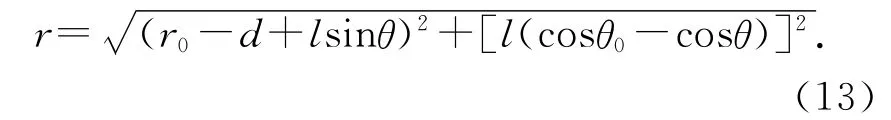
由同种电荷的电势能公式可知［12，13］

由于单摆球在右偏角θ0处合力为0，则有

由（7）、（13）-（15）式可得，单摆球在斥力作用下右偏θ角时的总势能为

若单摆球在右偏角θ0位置处于稳定平衡状态，单摆球的总势能Ep在θ0位置的一阶导数必须等于0，同时二阶导数必须大于0.

对（16）式在右偏角θ0位置求一阶导数，可得

对（16）式在右偏角θ0位置求二阶导数，可得

由图5可知，r0＞d，则由（18）式可知

由（17）、（19）式可知，单摆球在右偏角θ0位置处于稳定平衡状态.

在几何画板软件中绘制（16）式的函数图像如图6所示.由图6可知，在点电荷的静电斥力作用下，单摆球的总势能Ep在右偏角θ0处存在极小值，也说明单摆球在右偏角θ0位置处的平衡类型属于稳定平衡.

图6

3 结论

综上所述，竖直悬挂的单摆球在大质量球的万有引力作用下偏离平衡位置时，只有当单摆球与大质量球的距离大于单摆球偏离竖直线的距离的2倍时，单摆球才能在与大质量球的引力作用下保持稳定；当单摆球与大质量球的距离不大于单摆球偏离竖直线的距离的2倍时，单摆球无法在大质量球的引力作用下保持稳定.

在以横向库仑力（或万有引力）作用下的单摆球为背景命制创新型试题时，建议选择斥力类型；若要选择引力类型，则应该添加“单摆球与引力源的距离大于单摆球偏离竖直线的距离的2倍”的限制条件，保证单摆球能处于稳定平衡状态.

由上述分析可知，2021年上海市高考选择性考试物理卷第17题应该追加r0＞2d的限制条件.