ELM-Adaboost分类器在轴承故障诊断中的运用

胡 超，沈宝国，杨 妍，谢中敏

（江苏航空职业技术学院航空工程学院，江苏 镇江 212134）

1 引言

旋转机械系统中，轴承担任着承载和传递能力的重要地位，其性能状态能够决定机械是否能良好运行。由于轴承材料、制备工艺、工作环境等，导致轴承寿命离散度较大［1］，在长期使用过程中极易发生故障。在部分旋转机械中，由于轴承安装位置特殊或者长期浸泡在油液中，难以及时对轴承进行诊断。

在轴承的早期故障诊断中，常根据油液磨粒尺寸、材料［2］等对轴承进行故障诊断，但这种基于油液分析的方法往往受到诊断者的人为误差干扰。随着对转子动力学［3］的深入研究，根据物体的振动信号可实现故障的诊断。在文献［4-12］中，不少学者对故障振动信号进行分析，提取部分信号统计特征参数，并分别结合支持向量［4-6］、学习机［7-8］、人工神经网络［9-10］、Elman［11］和RBF网络［12］对轴承故障进行诊断，并取得较好的成果。但部分学者［8，11］认为单纯的诊断网络效果较差，因此常采用遗传算法、粒子群等进行优化，在他们的研究中证明了此方法的有效性，但在文献［13］中也论述了使用寻优算法优化诊断网络会导致诊断时间的成倍增加。在实时诊断过程中，诊断时间和准确性被同时提出要求，因此将多个基本分类器变成一个强分类器成为一种研究趋势［14］。在国内外学者的努力下，基于不同弱分类器的强分类器模型取得研究进展。文献［15］将SVM作为基本分类器，建立基于Ada-boost_SVM分类器的滚动轴承故障诊断模型；文献［16］将BP网络作为基本分类器，建立基于BP-AdaBoost的耦合碰摩故障特征识别模型；文献［17］将BP-AdaBoost算法用于列车关键零件故障识别；文献［18］将BP-AdaBoost算法用于机载燃油泵故障诊；文献［19］将ELM作为基本分类器，并结合图像局部纹理的特征描述，实现AdaBoost_ELM在人脸识别中的运用。

综上所有所述，在大多数基于弱分类器组合而成的强分类器中，多采用诸如BP神经网络的前馈神经网络。但由于部分单隐层前馈神经网络收敛速度慢、易陷于局部最优，因此Huang.G.B等［20］提出极限学习机能避免传统网络对学习速率、终止条件、易陷于局部极优等缺陷，因而广泛用于数据压缩、特征学习、聚类、诊断等领域［20］。基于极限学习机的这一特点，将极限学习机作为基本分类器组合成强分类器模型，能够较好的弥补单分类器的缺陷。将强分类器ELM-Adaboost模型用于滚动轴承故障诊断中，并着重分析影响到强分类器性能的参数。

2 ELM-Adaboost轴承故障诊断模型

文献［20］提出极限学习机（Extreme Learning Machine，ELM）算法，此算法能够避免部分前馈神经网络存在的易陷于局部极限值的缺陷，且其能够逼近任意非线性分段函数［21］。因此，被广泛的运用于分类、预测等领域［22］。其详细理论在文献［8］已详细介绍，此处不再累述。将多个基本分类器ELM模型通过Adaboost提升算法组合成一个强分类器，且对于ELM-Adaboost的诊断模型期待其输出结果直接为轴承故障类型标签。由于常见分类的Adaboost提升算法中，基本分类器Gm（x）前的系数ɑm之和≠1。因此需要对Adaboost进行适当调整。强分类器ELM-Adaboost模型流程图，如图1所示。

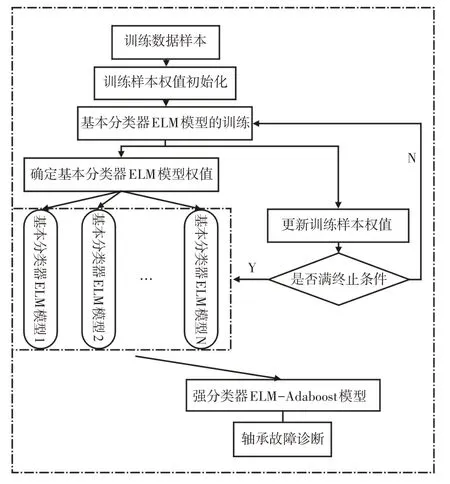
图1 强分类器ELM-Adaboost模型流程图Fig.1 Flow Chart of Strong Classifier ELM-Adaboost Model

假设训一个多分类的练数据集T=｛（x1，y1），（x2，y2），..，（xN，yN）｝，其中xi∈Rn，yi=｛1，2，3，4｝，则强分类ELM-Adaboost（x）可以通过下列方式进行计算。

Step1：对训练数据权值分布初始化：

Step2：循环m=1：M（M表示基本分类器数量）

（1）使用基本分类器ELMm（x）去训练数据，并计算权重误差：

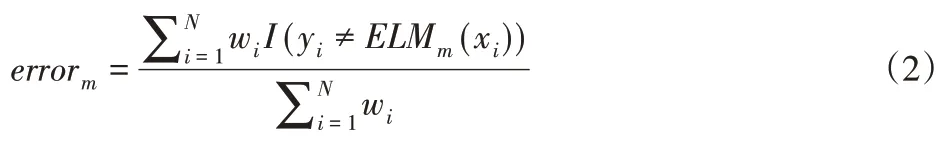
（2）计算第m个基本分类器的权重（k表示分类数）：

在转变教学理念重视互动教学时，教师也应积极建立培养和谐融洽平等的师生关系。师生关系的融洽与否对课堂教学质量的提升有重要的作用。如果教师与学生之间能够建立起和谐融洽、平等有爱的关系，教师关心爱护学生，学生信任尊重教师，那么在课堂学习中将会促使师生之间获得更好的交流沟通，提高互动教学质量，促进学生综合能力的提升。所以，教师应注重师生平等融洽关系的建立，为高中数学的课堂互动教学奠定良好基础。

（3）更新所有样本数据的权重：

Step3：循环所有分类器后，对基本分类器数量ɑm进行归一处理，输出ELM-Adaboost分类器：

式中：round（x）—取整函数。

将多个基本的分类器ELM模型组成强分类器模型后，能够提升分类器对故障的识别率和稳定性，在后续诊断过程中将进行论述。

3 ELM-Adaboost滚动轴承故障诊断

3.1 实验数据来源及处理方法

滚动轴承实验数据来自于美国西储大学轴承数据中心网站［24］。滚动轴承故障试验中采用6205-2RS-JEM-SKF型滚动轴承，轴承尺寸参数如表1所示；试验中，电机转动频率1730r/min，采用频率48kHz，采样4800组样本点。试验故障诊断中选择轴承正常状况和外环刮痕故障两种类型作为分析对象，每类故障提取数据样本600组。

表1 6205-2RS-JEM-SKF型轴承参数Tab.1 6205-2RS-JEM-SKF Type Bearing Parameters

3.2 最优时域参数的选择

考虑到时域特征参数之间数量级和量纲问题给诊断结果带来的误差，因此需要对时域特征参数按下式进行归一化。

式中：xmax、xmin—特征参量的最大值、最小值和平均值；

xi—某类特征参量的第i个值；

同时，考虑到特征变量之间存在的耦合性，使用SPSS软件对时域特征参数进行降维处理［25］。因子分析中采用α因子分析提取特征，选择累积方差达到99.463%的前5个因子作为诊断模型的输入参数，即：平均值、绝对值、峰峰值、均方根值、偏度。因此，经过数据归一化和因子降维后的时域变量，如表2所示。

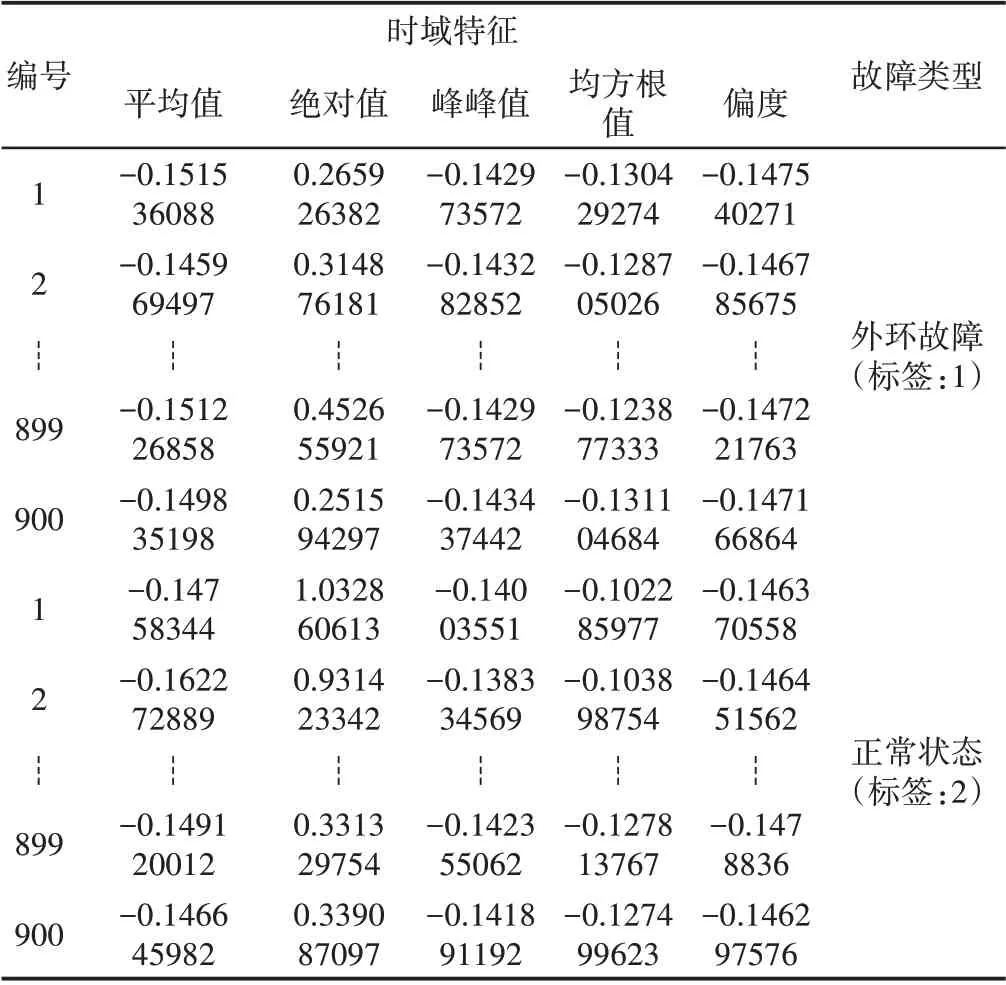
表2 诊断模型的输入参数Tab.2 Input Parameters of Diagnosis Method

3.3 ELM-Adaboost模型关键参数分析

强分类器ELM-Adaboost模型是由许多基本分类器ELM模型组成，而ELM模型隐含层的神经元数量、激活函数会影响到ELM模型的诊断效果［8］；另外，基本分类器ELM模型的数量也能影响到强分类器ELM-Adaboost模型的诊断效果。因此，需要先对强分类器ELM-Adaboost模型参数进行分析，再选择最优参数设置强分类器ELM-Adaboost模型进行后续轴承故障诊断。

在对分类器模型进行参数分析时，为保证后续诊断过程中参数对样本数据的适应性，直接采用轴承故障样本数据进行分析，可避免因为数据问题导致最优参数不适宜的现象。轴承故障数据样本共两类，每类样本数量900组，共计1800组样本数据，随机不重复选择1320组作为训练集样本数据，剩下480组作为测试集样本数据。

3.3.1 激活函数、神经元数量的影响

目前对于ELM分类器模型中参数的分析尚无行而有效的方法，因此采取遍历寻优。考虑到ELM分类器随机产生权值和阈值带来的数值不具复现性问题，对实验重复计算30次并计算结果的平均值作为依据。隐含层神经元数量、激活函数对基本分类器ELM模型和强分类器ELM-Adaboost模型的影响，如图2、图3所示。

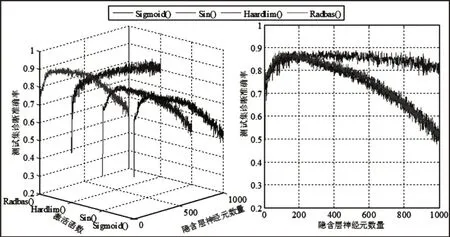
图2 基本分类器ELM模型Fig.2 Basic Classifier ELM Model

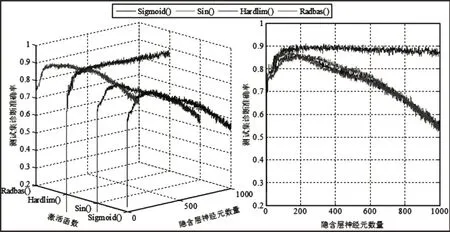
图3 强分类器ELM-Adaboost模型Fig.3 Strong Classifier ELM-Adaboost Model

从图2和图3可知，隐含层神经元数量无论是对基本分类器ELM模型还是对强分类器ELM-Adaboost模型的影响都很明显。当基本分类器ELM模型的激活函数为Radbas（）、Sin（）和Sigmoid（）时，隐含层神经元数量超过200之后，分类器对测试样本的诊断效果明显下降；当基本分类器ELM模型采用Hardlim（）函数时，分类器对测试样本的诊断准确率随着隐含层神经元数量增加而略微下降。对比图2和图3可知，基本分类器ELM模型对神经元数量较为敏感，而强分类器ELM-Adaboost模型敏感程度较小，具体表现在，分类器随着神经元数量变化其诊断准确率波动的明显程度。另外，由图2和图3观察可知，对于轴承故障诊断无论是采用基本分类器ELM模型还是采用强分类器ELMAdaboost模型，激活函数选择Hardlim（）函数效果较好；且整体而言，强分类器ELM-Adaboost模型相比基本分类器ELM模型的诊断效果较佳。

3.3.2 ELM模型数量对ELM-Adaboost模型的影响

为了选择更加合适数量的基本分类器ELM模型组成强分类器ELM-Adaboost模型，在基本分类器ELM模型隐含层激活函数采用Hardlim（）、隐含层神经元数量为229时，对强分类器中基本分类器ELM模型的数量进行分析。研究分析基本分类器数量从1到100时，强分类器ELM-Adaboost模型对轴承故障测试集样本的准确率变化趋势；与此同时，在选择基本分类器ELM模型组成强分类器ELM-Adaboost模型时，准确率和时间耗费率均作为考虑成本因素之一。经过计算，强分类器ELM-Adaboost模型诊断准确率随基本分类器ELM模型的变化趋势如图4右所示，耗费时间变化趋势如图4左所示。

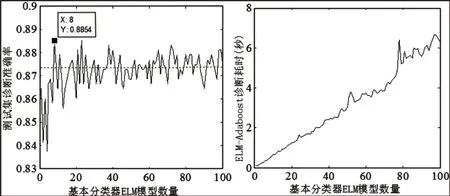
图4 基本分类器ELM模型数量对强分类器ELM-Adaboost模型的影响Fig.4 Effect of the Number of Basic Classifier ELM Models on Strong Classifier ELM-Adaboost Model

由图4可知，随着基本分类器ELM模型数量的变化，强分类器ELM-Adaboost模型的诊断准确率大概在87.3%左右波动，往复波动率不超过4%，可见强分类器ELM-Adaboost模型具备一定的稳定性；且其诊断准确率明显均＞83%，未曾出现如图3和图4所示诊断率存在低于80%的情况，这主要跟神经元数量设置有关；另外随着基本分类器ELM模型数量的增加，强分类器ELMAdaboost模型诊断耗时持续增长。

经过3.2.1节和3.2.2节对强分类器ELM-Adaboost模型中的关键参数分析，在后续采用强分类器ELM-Adaboost模型进行诊断过程中，隐含层神经元激活函数采用Hardlim（）函数，隐含层神经元数量为229。

3.4 轴承故障诊断结果分析

为验证强分类器ELM-Adaboost模型在轴承故障诊断中的有效性，从1800组轴承故障样本数据中随机不重复的选择1320组作为训练集样本数据，剩下480组作为测试集样本数据；另外，基本分类器ELM模型、强分类器ELM-Adaboost模型中，隐含层神经元激活函数均采用Hardlim（）函数，隐含层神经元数量设置为229。为避免ELM随机产生初始值权值和阈值给诊断结果带来的不可复现性，重复诊断30次并计算其均值，如表4所示。

由表4可知，强分类器ELM-Adaboost模型无论是对于正常轴承还是外环故障轴承的诊断效果均比基本分类器ELM模型好。基本分类器ELM模型对外环故障的诊断效果比对正常轴承的诊断效果要好近3个百分点；而强分类器ELM-Adaboost模型对于正常轴承和外环故障轴承的诊断效果差距较小。综上所述，强分类器ELM-Adaboost模型具有诊断效果明显、诊断结果波动性较小等优点，因此相比于基本分类器ELM模型更适合于轴承故障诊断中。

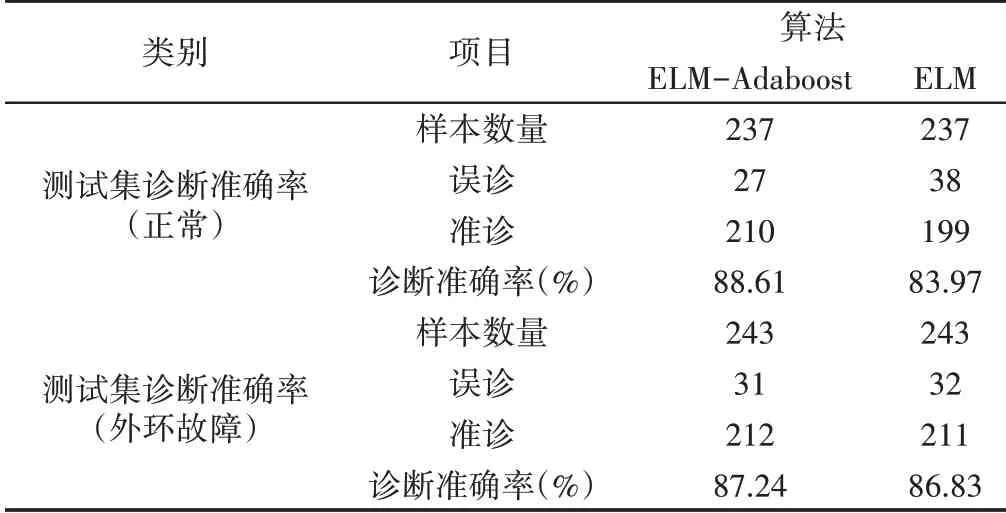
表4 诊断结果Tab.4 Diagnostic Results

4 结论

将多个基本分类器ELM模型组合成强分类器ELM-Adaboost模型，从而实现滚动轴承故障诊断。首先，从滚动轴承振动信号中提取多个时域特征参数，考虑到参数之间存在的耦合性和维度灾难问题，采用因子分析法实现变量降维处理。其次，考虑到样本数据自身对最优参数设置带来的问题，因此基于轴承故障样本数据对基本分类器ELM模型和强分类器ELM-Adaboost模型中的隐含层神经元数量、激活函数进行分析，研究结果表明：隐含层神经元数量严重影响到分类器的诊断准确率；隐含层激活函数采用Hardlim（）的效果比其它激活函数的效果要好；强分类器ELM-Adaboost模型对隐含层神经元数量变化引起的诊断准确率波动性，敏感程度较低；在选择基本分类器ELM模型数量组成强分类器时，并非基本分类器越多效果越明显，在选择时应同时考虑到诊断准确率和诊断时间。最后，将基本分类器ELM模型和强分类器ELM-Adaboost模型用于滚动轴承故障诊断中，其诊断结果表明：强分类器的诊断效果好于基本分类器；在30次重复诊断过程中，强分类器的诊断准确均达到84%以上，而基本分类器则在78%以上，且重复诊断过程中强分类器的波动敏感性较低。