直觉模糊序决策系统的部分一致约简*
2019-04-18杜文胜
杜文胜
郑州大学 商学院,郑州 450001
1 引言
粗糙集理论[1]是由波兰学者Pawlak提出的一种能够处理不精确、不确定和不完备信息的软计算工具。该理论现已成功应用于人工智能、数据挖掘、模式识别与管理决策等领域[2-3]。需要指出的是,经典的粗糙集理论以等价关系(不可区分关系)为基础,然而,在现实世界中很多问题是基于优势关系的,如学生评教、教师职称评定以及学校学科评估。为了解决这类问题,Greco等提出了优势粗糙集理论[4],经过近二十年的发展,现已发展成为粗糙集理论的一个重要分支[5]。
保加利亚学者Atanassov提出了直觉模糊集的概念[6],它提供了元素属于此模糊概念的隶属度、非隶属度和犹豫度这三方面的信息,可同时表示肯定、否定和介于肯定与否定之间的犹豫性。由于其在处理模糊性和不确定性等方面的灵活性和实用性,有关该理论的研究受到了国内外相关领域学者的极大关注,并被应用于医疗诊断、专家系统、近似推理、机器学习和市场预测等领域[7-8]。
近年来,将优势粗糙集理论与直觉模糊集理论相结合成为研究的一个热点[9-11],研究的主题是直觉模糊序信息系统的属性约简,其中包括一致直觉模糊序决策系统的相对约简。针对不一致直觉模糊序决策系统,国内学者提出了分布约简和最大分布约简,并证明了二者的等价性[12-13]。另外,与基于等价关系的不一致系统类似[14-15],序决策系统还存在分配约简[16]、部分一致约简[17]以及其他形式的约简[18-20]。徐伟华等将分配约简引入到直觉模糊序决策系统[21],并将部分一致约简推广到区间值模糊序决策系统的情形[22],但对直觉模糊序决策系统目前尚未展开相关的讨论。
本文提出直觉模糊序决策系统的部分一致约简,得到了部分一致约简的判定定理,然后构造部分一致辨识矩阵和辨识函数,建立了求解直觉模糊序决策系统所有的部分一致约简的具体方法,并通过实例验证该方法的有效性。同时,证明了下约简和下近似约简与部分一致约简等价,从而进一步丰富了优势粗糙集理论。
2 直觉模糊序决策系统
传统的模糊集[23]给出了论域中元素的隶属度,而直觉模糊集不仅给出了隶属度,而且还给出了非隶属度。
定义1[6]论域U上的直觉模糊集是下列形式的对象:
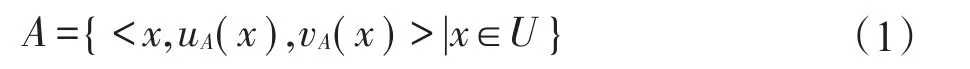
其中,uA(x)为x属于A的隶属度,vA(x)为x的非隶属度,并且满足关系式0≤uA(x)+vA(x)≤1,∀x∈U。
定义 2[24](格(L*,≤L*))为方便说明,记L*={(x1,x2)∈ [0,1]2|0≤x1+x2≤1},L*上的序关系≤L*如下:

定义3称四元组S=(U,C⋃{d},V,f)是一个直觉模糊序决策系统,其中U为有限非空对象集;C为有限非空条件属性集,d为决策属性,且C⋂{d}=∅;V为属性值值域;f为对象属性值映射。即,U={x1,,Vc为条件属性c的值域,其中每个元素均为直觉模糊元[25],且它们之间的序关系由定义2确定。对象属性值映射f:U×C→V,且 f(x,c)∈Vc,即 f(x,c)=(uc(x),vc(x)),∀x∈U。决策属性值映射f(x,d)∈{1,2,…,m},值域为有序实值。
若vc(x)=1-uc(x),∀x∈U,∀c∈C,则该系统退化为普通的模糊序决策系统。
定义4如果成立,称x关于属性c占优y,并记为x≻cy。称x关于属性集A占优y,记为x≻Ay,若x≻cy,∀c∈A。
注1由于≤L*是L*上的一个偏序关系,x≻cy与y≻cx可能同时不成立。
在直觉模糊序决策系统中可定义关于条件属性集和决策属性的优势关系,记:,。记为关于条件属性集A占优x的集合,则。另外,其中。
定义5[11]设S=(U,C⋃{d},V,f)是直觉模糊序决策系统,,则关于条件属性集B的下近似为:
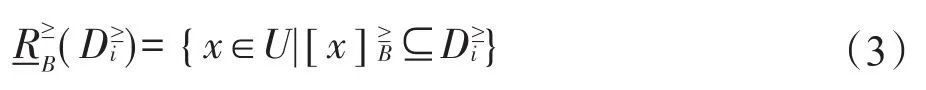
定义6[9]设S=(U,C⋃{d},V,f)是直觉模糊序决策系统,若,则称该系统为一致的,否则该系统为不一致的。
直观地,直觉模糊序决策系统是不一致的,如果存在x,y∈U,有x≻Cy,但是 f(x,d) Table 1 Intuitionistic fuzzy ordered decision system表1 直觉模糊序决策系统 例1如表1所示,S=(U,C⋃{d},V,f)是一个直觉模糊序决策系统,其中,U={x1,x2,…,x8},C={a1,a2,…,a5}。 设S=(U,C⋃{d},V,f)是直觉模糊序决策系统,对x∈U,B⊆C,记:称δB(x为)x关于条件属性集B的部分一致函数。 例2计算表1给出的不一致直觉模糊序决策系统中各元素关于属性集C的部分一致函数。 经计算得: 因此: 命题1设S=(U,C⋃{d},V,f)是直觉模糊序决策系统: (1)若B⊆A⊆C,则对任意x∈U有δB(x)⊆δA(x)。 (3)直觉模糊系统为一致的充要条件是δC(x)=其中i=f(x,d)。 定义7设S=(U,C⋃{d},V,f)是直觉模糊序决策系统,若对任意x∈U有δB(x)=δC(x),则称B为系统S的部分一致协调集。更进一步,若B的任何真子集均不为部分一致协调集,则称B为系统S的部分一致约简。 命题2设S=(U,C⋃{d},V,f)是一致直觉模糊序决策系统,则B为部分一致协调集⇔B为相对协调集。 证明若,则称B为相对协调集[9]。B为相对协调集 推论1设S=(U,C⋃{d},V,f)是一致直觉模糊序决策系统,则B为部分一致约简⇔B为相对约简。 证明若B为部分一致约简,则B为部分一致协调集,而B的任何真子集均不为部分一致协调集,由命题2得:B为相对协调集且B的任何真子集均不为相对协调集,因此B为相对约简。反之亦然。 推论1表明部分一致约简为相对约简在不一致系统中的有效推广。下面给出部分一致约简的判定定理。 定理1设S=(U,C⋃{d},V,f)是直觉模糊序决策系统,则B为部分一致协调集⇔对任意x,y∈U,当δC(y)⊄ δC(x)时,有[x]≥B⊄[y]≥B。 证明“⇒”(反证法)若当时,有,进而由命题 1(2)得。由 B为部分一致协调集,于是有δB(x)=δC(x),∀x∈U。综上可得 δC(y)⊆δC(x),这与假设 δC(y)⊄δC(x)相矛盾,因此结论成立。 “⇐”若对任意 x,y∈U,当 δC(y)⊄δC(x)时,有成立 。因此当,可得 另一方面,由命题1(1)有δB(x)⊆δC(x),综上所述有δB(x)=δC(x),即B为部分一致协调集。 定义8设S=(U,C⋃{d},V,f)是直觉模糊序决策系统,记D*δ={(x,y)|δC(y) ⊄ δC(x)},定义: 称Dδ(x,y为)对象x和y的部分一致辨识属性集。矩阵Dδ={Dδ(x,y)|x,y∈U}为该系统的部分一致辨识矩阵。 例3计算表1给出的不一致直觉模糊序决策系统的部分一致辨识矩阵。 Table 2 Partially consistent discernibility matrix表2 部分一致辨识矩阵 由 例 2 知 D*δ={(x1,x2),(x1,x8),(x3,x1),(x3,x2),(x3,x7),(x3,x8),(x4,x1),(x4,x2),(x4,x7),(x4,x8),(x5,x1),(x5,x2),(x5,x7),(x5,x8),(x6,x1),(x6,x2),(x6,x7),(x6,x8),(x7,x2),(x7,x8)}。由此可计算此直觉模糊序决策系统的部分一致辨识矩阵,如表2所示(为简化表达,辨识矩阵中∅未列出)。 定理2设S=(U,C⋃{d},V,f)是直觉模糊序决策系统,B⊆C,则B为部分一致协调集⇔对任意(x,y)∈D*δ,有B⋂Dδ(x,y)≠∅。 证明“⇒”对任意(x,y)∈D*δ,即 δC(y)⊄δC(x),由 B 为部分一致协调集则 [x]≥B⊄[y]≥B。因此存在a∈B,使得(x,y)∉R{a},≥即 a∈Dδ(x,y)。于是有B⋂Dδ(x,y)≠∅成立。 “⇐”若对任意 (x,y)∈D*δ即 δC(y)⊄δC(x),有B⋂Dδ(x,y)≠∅,则存在a∈B使得(x,y)∉R{≥a},因此x∉ [y]≥a,且x∉[y]≥B。另外,显然 x∈[xa]≥B,从而[x]≥B⊄[y]≥B。由定理1知B为部分一致协调集。 老人旁若无人地专注于写字,又何尝不是“只记花开不记人”的境界呢?没有功利性,才能无拘无束地追求精神的愉悦。有了追求,就有了精神寄托,用追求喂养精神,就能成为精神上明亮的人。 定义9设S=(U,C⋃{d},V,f)是直觉模糊序决策系统,Dδ为S的部分一致辨识矩阵,记: 称Fδ为该决策系统的部分一致辨识函数。 定理3设S=(U,C⋃{d},V,f)是直觉模糊序决策系统,Fδ为该决策系统的部分一致辨识函数,Fδ的最小析取范式为: 证明直接由定理2和最小析取范式的定义可得。 例4计算表1给出的不一致直觉模糊序决策系统所有的部分一致约简。 可以计算得: 即此系统的部分一致约简为{a2,a4}和{a4,a5}。 接下来将本文提出的部分一致约简与其他形式的约简进行比较。对象x关于条件属性集B的(最大)分布函数为[12-13]: 根据计算得: 系统的(最大)分布约简和分配约简为各对象均保持与关于C的(最大)分布函数和分配函数相同的极小子集[12-13,21]。可以验证{a2,a4}为系统的(最大)分布约简,{a2,a3}和{a2,a4}为系统的分配约简。可以证明(最大)分布约简为部分一致协调集。事实上,B为(最大)分布约简,则根据定义7,显然B为部分一致协调集。另外,可以验证{a2,a3}不为部分一致约简,而{a4,a5}也不为分配约简,因此,部分一致约简和分配约简之间并无关联。 本章介绍与部分一致约简等价的两种约简形式。 设S=(U,C⋃{d},V,f)是直觉模糊序决策系统,对B⊆C,记: 命题3设S=(U,C⋃{d},V,f)是直觉模糊序决策系统: (1)对任意B⊆C,有1≤λB≤m。 定义10设S=(U,C⋃{d},V,f)是直觉模糊序决策系统,对B⊆C,若λB=λC,则称B为系统S的下协调集。更进一步,若B的任何真子集均不为下协调集,则称B为系统S的下约简。 定理4设S=(U,C⋃{d},V,f)是直觉模糊序决策系统,则B为部分一致协调集⇔B为下协调集。 证明“⇒”设B为系统的部分一致协调集,即对任意x∈U有δB(x)=δC(x)。则对任意Di≥(i≤m): “⇐”设B为下协调集,则λB=λC成立。即: 因此δB(x)=δC(x),B为系统的部分一致协调集。 推论2设S=(U,C⋃{d},V,f)是直觉模糊序决策系统,则B为部分一致约简⇔B为下约简。 证明证明过程和推论1的证明类似。 在文献[11]中,Xu等引入了下近似协调集和下近似约简的概念,下面证明这两个概念分别与下协调集和下约简等价,进而与本文介绍的部分一致协调集和部分一致约简分别等价。 定理5设S=(U,C⋃{d},V,f)是直觉模糊序决策系统,则B为下近似协调集⇔B为下协调集。 证明B为下近似协调集,即B为下协调集。 推论3设S=(U,C⋃{d},V,f)是直觉模糊序决策系统,则B为下近似约简⇔B为下约简⇔B为部分一致约简。 证明证明过程和推论1的证明类似。 例5验证{a2,a4}和{a4,a5}为表1给出的不一致直觉模糊序决策系统所有的下约简和下近似约简。 可以计算得: 取B={a2,a4}或{a4,a5},则: 因此,{a2,a4}和{a4,a5}为系统的下协调集和下近似协调集。同时可以验证任何真子集均不为下协调集或下近似协调集。 另外,可以验证C的其他子集均不为下约简或下近似约简。因此,{a2,a4}和{a4,a5}为系统所有的下约简和下近似约简。 本文提出了基于优势关系的直觉模糊决策系统的部分一致约简,证明了其在系统一致的情形下与相对约简等价,给出了部分一致约简的判定定理,提供了利用部分一致辨识矩阵和辨识函数求解系统所有的部分一致约简的方法,进一步丰富了优势粗糙集理论的研究内容。同时,讨论了部分一致约简与(最大)分布约简以及分配约简应满足的条件间的强弱关系。具体地,(最大)分布约简的条件较部分一致约简的条件强,而部分一致约简与分配约简间无强弱关系。另外,给出了部分一致约简的两种等价形式:下约简和下近似约简。从其他角度阐释部分一致约简是决策系统的一种有意义的约简。
3 部分一致约简

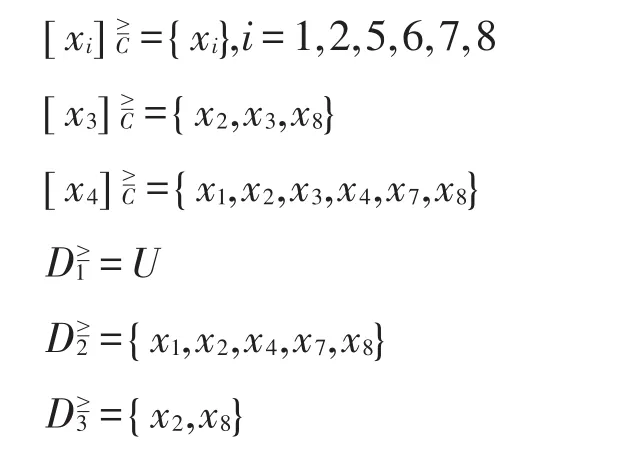
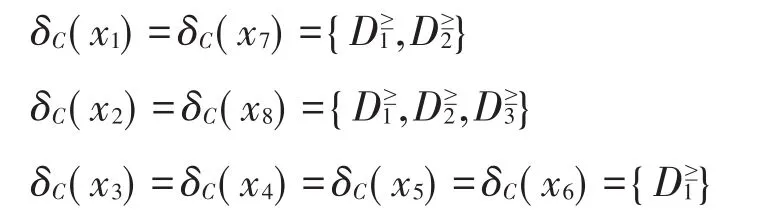



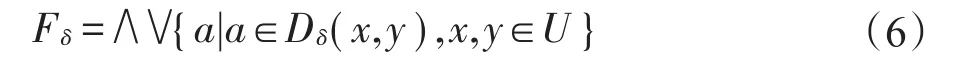

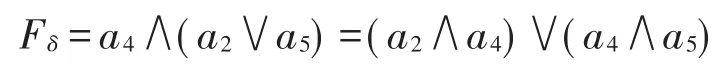

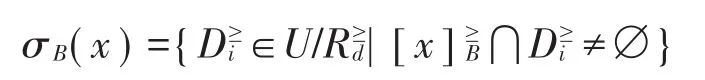
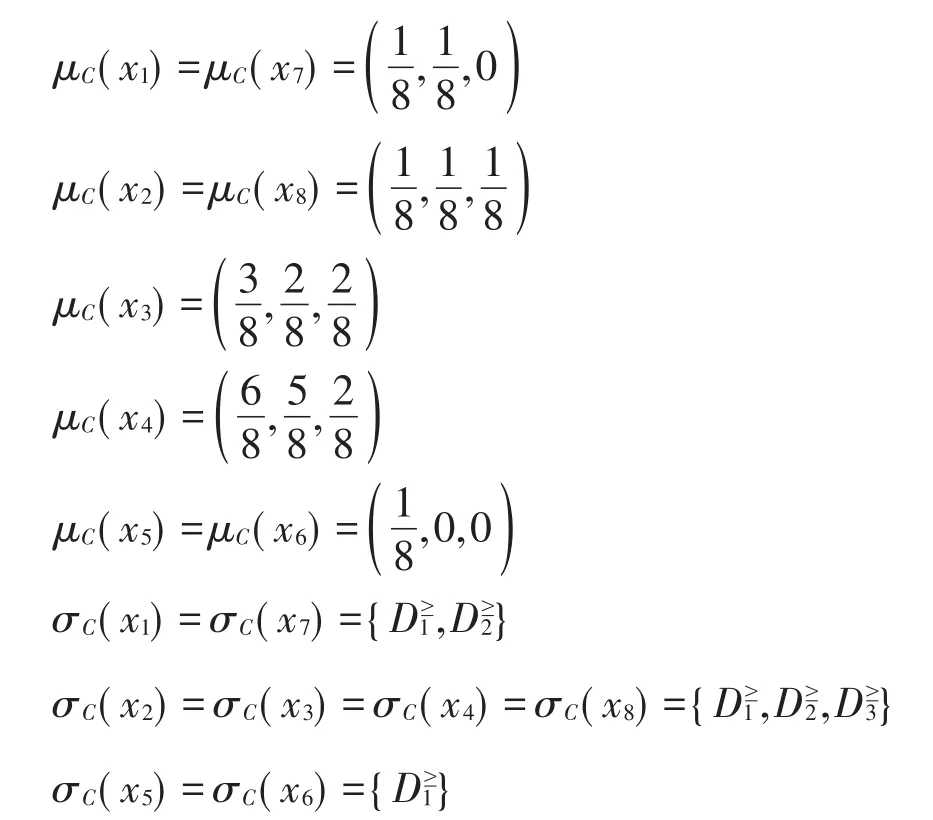
4 部分一致约简的等价定义

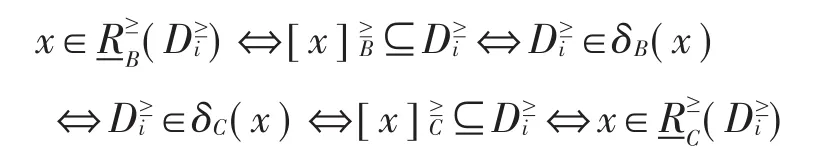
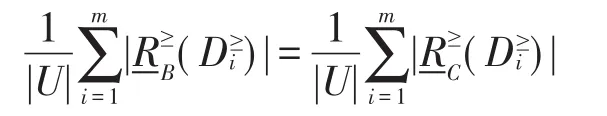

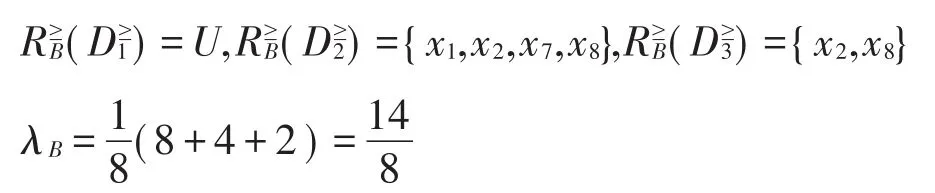

5 结束语
