带长法兰汽车多楔轮静动态分析与结构优化
2022-02-22周金朝刘蕾王召宇石文超李萍薛克敏
周金朝,刘蕾,王召宇,石文超,李萍,薛克敏
带长法兰汽车多楔轮静动态分析与结构优化
周金朝a,刘蕾a,王召宇a,石文超b,李萍a,薛克敏a
(合肥工业大学 a. 材料科学与工程学院;b. 工业与装备技术研究院,合肥 230009)
为研究带长法兰汽车多楔轮的结构稳定性,实现零件轻量化,对多楔轮结构进行仿真研究和优化设计。通过建立有限元模型,使用ANSYS有限元软件进行不同齿数结构汽车多楔轮静动态分析,研究其变形量、应力分布规律及固有频率的变化情况。仿真结果表明,一阶至六阶的固有频率为56.62~1691.90 Hz,三齿为多楔轮最优齿数结构,其结构稳定性好,传动效率高。在实际工况中,激励源应避免出现在轴和轴方向。结构优化后的带长法兰汽车三齿多楔轮质量减少了3.2%,刚度基本不变,强度增加,为汽车多楔轮实际结构设计提供了一定的参考价值。
带长法兰多楔轮;模态分析;静力学分析;结构稳定性;形状优化
随着发动机新技术的革新以及在国家大力倡导发展新能源汽车的大背景下,汽车轻量化成为发展重点,对多楔轮的性能要求也越来越严格[1-2]。多楔轮作为汽车重要组件,广泛应用于节能汽车、新型混合动力汽车动力系统、电机和各种机械装备的带传动及减震器中。文中研究的带长法兰汽车多楔轮具有局部多楔齿、底部长法兰、顶部凸筋及双筒壁等复杂结构特征,其传统加工方法[3-4]是采用铸、锻毛坯经切削加工而成,材料的利用率及生产效率低,产品精度差,体积大,转动惯量大,应用市场小。采用金属板材整体旋压成形,得到的零件强度高、金属流线完整、生产效率高、成本低,在汽车行业应用前景广阔。
优化零件结构,提高综合性能,实现多楔轮轻量化是未来发展的重点。多楔轮的强度不足会影响传动的稳定性,严重影响汽车的安全性和可靠性,甚至会造成安全事故。解芳等[5]研究了不同结构发动机水泵带轮内部的应力分布情况,通过结构优化设计,发现凹凸实心式结构带轮的结构稳定性较好,可以有效提高带轮的强度。陈思思[6]研究了汽车同步带齿形对传动过程稳定性的影响,研究发现齿形会直接影响带传动过程中的振动和噪声性能,并且通过试验测试,获得了齿形对同步带传动固有频率的影响变化规律。现有关于多楔轮的报道,大多是关于其成形工艺的研究以及造成成形缺陷的原因和避免方法[7-9],而对多楔轮零件结构本身(如齿数、倾角、齿高等关键参数)的强度分析及结构优化设计的研究,至今鲜有报道。
文中进行了不同齿数结构带长法兰汽车多楔轮的静动力学分析,研究其结构稳定性变化情况和最优齿数结构多楔轮的振型变化规律,并在此基础上结合形状优化方法对最优齿数多楔轮进行结构优化,使改进后的带长法兰汽车多楔轮零件在满足刚强度要求的同时实现减重,为实际结构设计和生产提供理论指导。
1 零件结构特征
多楔轮的齿数结构会影响发动机性能。图1为带长法兰多楔轮零件结构,可看出该零件整体壁厚分布不均匀,结构特征复杂。零件具有局部多楔齿和双筒壁结构,顶部具有凸筋,底部具有一定倾角的长法兰结构,内筒底部具有花键。
2 有限元模型的建立
考虑到较少的齿数能够使传动的结构紧凑,改善多楔轮轮齿的应力分布,匹配合适尺寸的传动带,使用Proe建立了3种不同齿数的带长法兰汽车多楔轮模型,3种多楔轮模型中齿高、齿宽等结构参数值均相同,如图2所示。材料选取AISI-1008号钢,其密度为7.85 g/cm3,屈服强度为220 MPa,弹性模量为210 GPa,泊松比为0.3,硬化模量为1000 MPa。
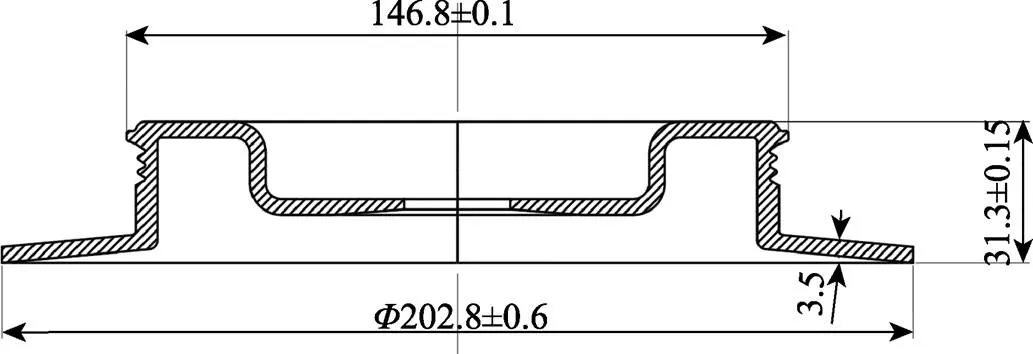
图1 某带长法兰多楔轮零件结构

图2 不同齿数带长法兰汽车多楔轮模型剖视图
2.1 载荷和约束
图3为多楔轮载荷和约束示意图。模拟使用ANSYS仿真软件,其中,方向为多楔轮的轴向方向,从多楔轮上部指向底部,和方向分别为多楔轮相互垂直的两个径向方向。依据实际工况,将约束与载荷施加在整个多楔带轮上。
根据带长法兰汽车多楔轮的加载条件,多楔轮中间平面受沿轴向的压力,表示沿轴正向2400 N的压力。多楔轮轮齿上受预紧力和弯矩,表示沿轴负方向大小为450 N的预紧力,为楔形齿上沿轴方向大小为0.033 N·mm的弯矩。中间轴孔在工作时受与预紧力相反的径向压力以及与轮齿相反的弯矩,同时受轴向约束以及支撑约束,表示沿着轴正方向大小为450 N的力,为沿轴的大小为−0.033 N·mm的弯矩,为沿轴向的固定约束,为对轴孔施加的压紧支撑约束。底部花键受轴向约束的作用,为对多楔轮底部花键施加的轴向约束,代表对整个多楔轮施加的旋转速度(为20 rad/s)。
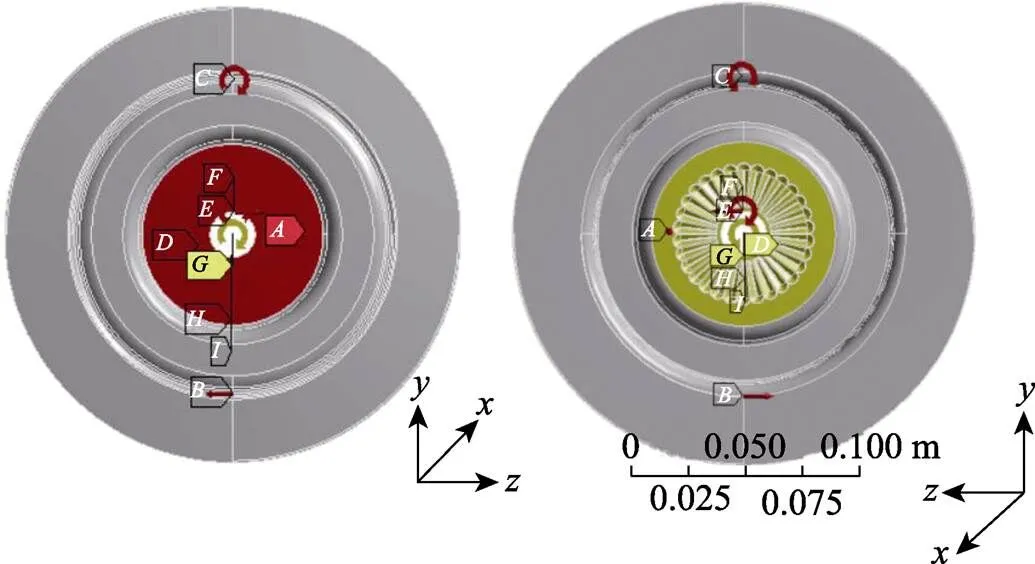
图3 载荷和约束示意
2.2 网格划分
在有限元模拟中,网格划分质量会影响模拟结果的准确性,因此需要对网格进行一定的优化。优化后网格划分情况如图4所示,其中图4a—c分别为一齿、二齿和三齿带长法兰汽车多楔轮,网格数量分别是48 059,49 073,52 204,网格类型为四面体单元。
3 结果与分析
3.1 静力学分析
静力学分析中,最大变形量反映了结构的刚度,最大应力值反映了材料的强度[10]。图5为3种齿数结构多楔轮的变形量分布云图和应力分布云图。图6为不同齿数带长法兰汽车多楔轮的最大变形量和最大应力的对比。
从图5和图6可以看出,随着零件内筒壁过渡到长法兰处,多楔轮变形量均逐渐增加,并且在最外圈法兰处均出现了最大变形,齿部的变形量均小于外圈法兰处。随着齿数增加,多楔轮最大变形量值逐渐降低。二齿多楔轮的最大变形量为1.16×10–2mm。三齿多楔轮的最大变形量最小,为1.06×10–2mm,与一齿多楔轮相比,降低了49.32%。表明在承受相同载荷和约束的情况下,三齿结构可以均分载荷,使单个齿承受的载荷更均匀,降低外圈法兰处的载荷,从而降低零件的变形量。
不同齿数带长法兰汽车多楔轮的整体应力分布均匀,最大应力值均集中出现在内筒壁轴孔处。这是因为轴孔处是载荷和约束密集区,受力情况复杂。随着齿数的增加,最大应力值先降低后增加。三齿多楔轮的最大应力值为41.48 MPa,与一齿多楔轮相比,降低了5.32%,与二齿多楔轮相比,增加了1.58%。表明齿数的增加会影响轴孔处应力分布,造成应力增加,也说明了多楔轮齿数不能过多。另外,也从侧面说明了轴孔处为结构优化的重要参考区域。最大应力出现的位置,会出现磨损情况,可能会成为破坏的潜在危险点,需要进行适当的润滑或者增加相应的壁厚。结合变形量和应力的分析,与其他2种多楔轮结构相比,三齿带长法兰汽车多楔轮具有较好的刚度和强度。

图4 不同齿数带长法兰汽车多楔轮的网格划分
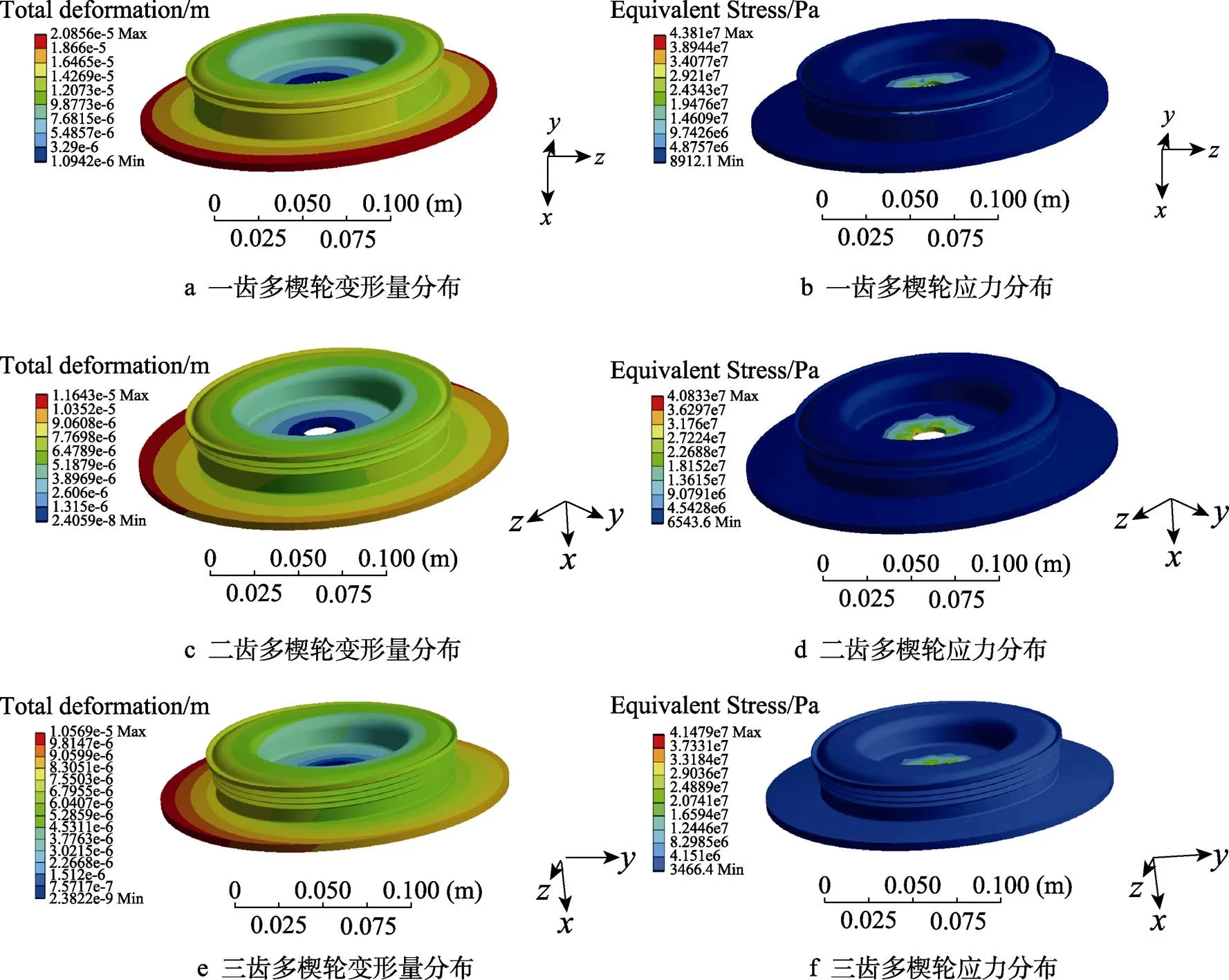
图5 不同齿数带长法兰汽车多楔轮变形量和应力分布云图
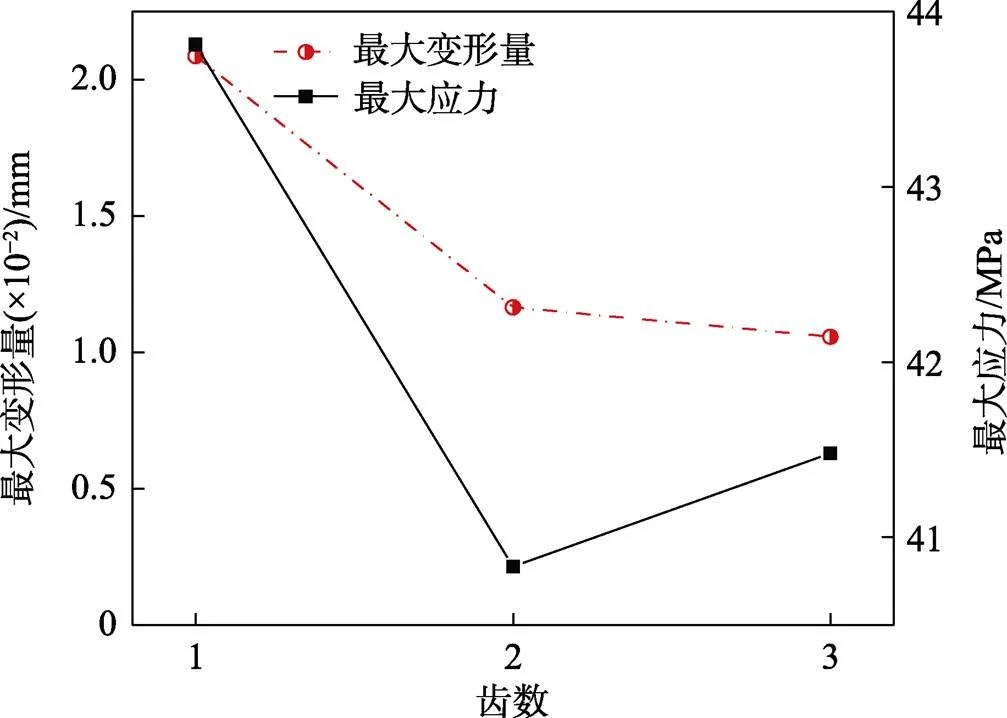
图6 不同齿数带长法兰汽车多楔轮的最大变形量和最大应力的对比
3.2 模态分析
模态分析用于确定设计结构振动的固有特性,即结构的固有频率[11-12]。图7为不同齿数带长法兰汽车多楔轮在约束模态不同阶数下的固有频率对比[13]。
如图7所示,随着模态阶数的增加,不同齿数多楔轮的模态固有频率均逐渐增加。一齿多楔轮固有频率的最大变化速率出现在三阶到四阶,二阶到三阶和四阶到五阶的固有频率变化速率较小。三齿多楔轮的固有频率在一阶到二阶的变化速率最大,三阶到四阶的变化速率最小。其中,三齿多楔轮的一阶固有频率最小,为56.62 Hz,与一齿多楔轮相比,减小了40.93%。三齿多楔轮的六阶固有频率也小于同阶下的二齿和三齿多楔轮,为1691.90 Hz。对于结构复杂的多齿带长法兰汽车多楔轮,当激励源的振动频率接近部件固有频率,并且频率方向相同时,将会出现共振现象,造成多楔轮损坏,进而影响整个系统的稳定性,出现事故[14-15]。因此,为了避免机器和零件产生共振,提升零件的使用寿命,在进行结构设计时,应将激振力的频率与系统的固有频率错开,设计合理的缓震环境。通过模态分析,发现3种齿数多楔轮结构的固有频率范围基本一致。结合前述的静力学分析,表明三齿多楔轮有更好的结构稳定性,因此确定其为最优结构。
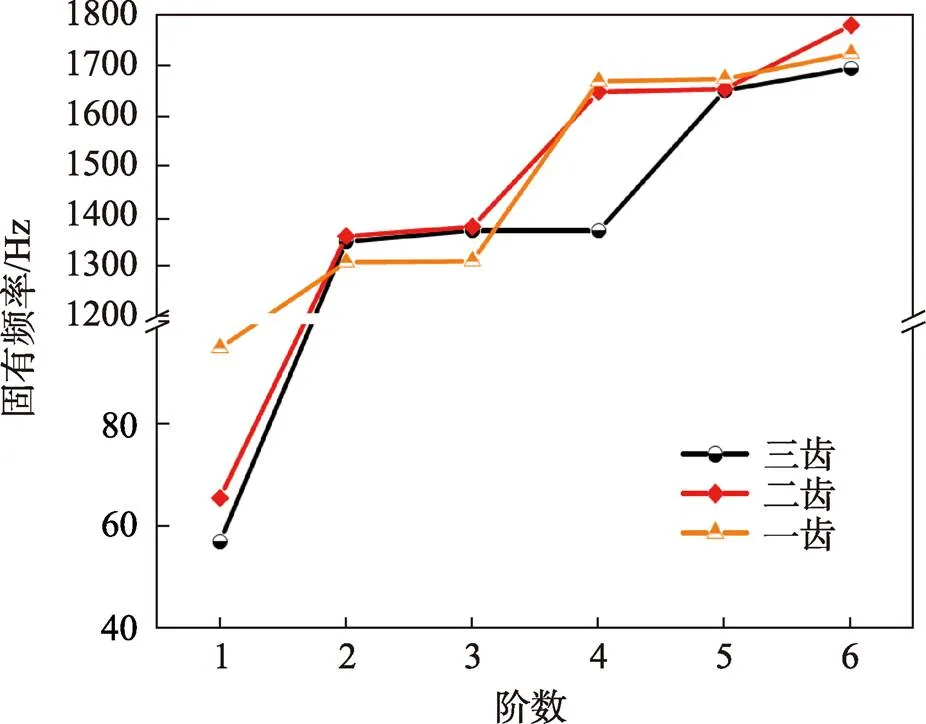
图7 不同齿数带长法兰汽车多楔轮的阶数-固有频率曲线
3.3 三齿结构带长法兰汽车多楔轮模态振型分析
为进一步研究多楔轮的结构稳定性,选用最优三齿多楔轮进行振型分析。图8为三齿带长法兰汽车多楔轮约束模态下的前六阶振型。
通过对求解器输出信息和振型云图的分析,获得了不同模态阶数下三齿多楔轮的振型变化规律。从图8a可知,一阶振型没有出现明显的弯曲和扭动。二阶振型中,模型绕轴扭转振动,一端出现翘曲。翘曲会影响各零部件的装配,造成多楔轮的磨损。三阶振型也出现了翘曲,翘曲的部位与二阶振型发生的部位不同。在多楔轮转动情况下,一端的翘曲会影响多楔轮受力的稳定性,降低零件使用寿命。图8d为四阶振型,模型绕轴张合弯曲振动,弯曲方向为轴正负方向,已经影响了零件的形状,使用性能大大降低,会对发动机等造成损坏。五阶振型也出现了张合弯曲振动,法兰和外筒壁处均出现了明显翘曲,会影响各零部件的传动。六阶振型为模型整体沿轴方向出现翘曲,会降低皮带的使用寿命。
以上振型分析可知,三齿带长法兰汽车多楔轮不仅有张合弯曲振动,还有扭转振动。这些振动会影响整个装配的稳定性和安全性。因此,在结构设计和工装实验中需要调整局部刚度和阻尼,抑制上述各种振动现象的发生[16-17]。
4 结构优化
通过前述模态分析,获得了最优三齿带长法兰汽车多楔轮的模态振型规律。为实现多楔轮零件轻量化和提升其力学性能,对三齿多楔轮进行了结构优化设计。
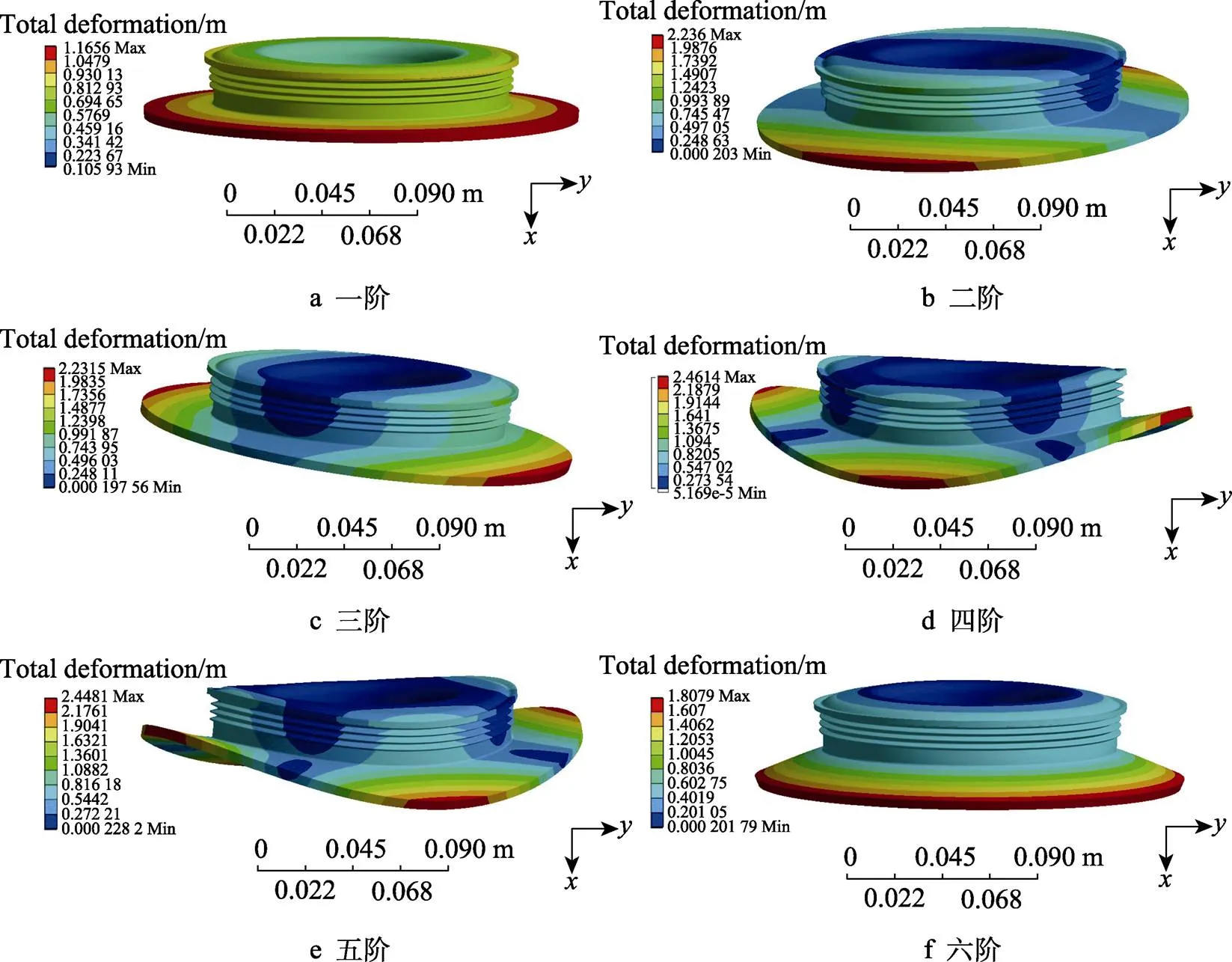
图8 三齿带长法兰汽车多楔轮不同阶数下的振型图
结构优化设计包含尺寸优化、形状优化和拓扑优化[18]。文中采用的是形状优化,形状优化的目的是减重,方法是shape optimization模块。通过给定结构参数(如约束、载荷、材料属性等)和需要减小的材料百分比(系统默认值为20%)即可实现类似于拓扑优化的优化效果,如图9所示。从图9可看出,红色部分为软件建议去除的部分,浅棕色为过渡区域,深灰色为需要保留的部分。根据结构优化计算结果,在保证结构强度刚度要求、保证结构功能要求、保证加工可行性的原则下[19],对零件结构进行了如下改进:① 内筒壁轴孔处厚度均匀增加;② 长法兰处均匀减薄,并做倒圆角处理;③ 外筒壁上方增加3处工艺孔。改进后的多楔轮结构如图10所示。
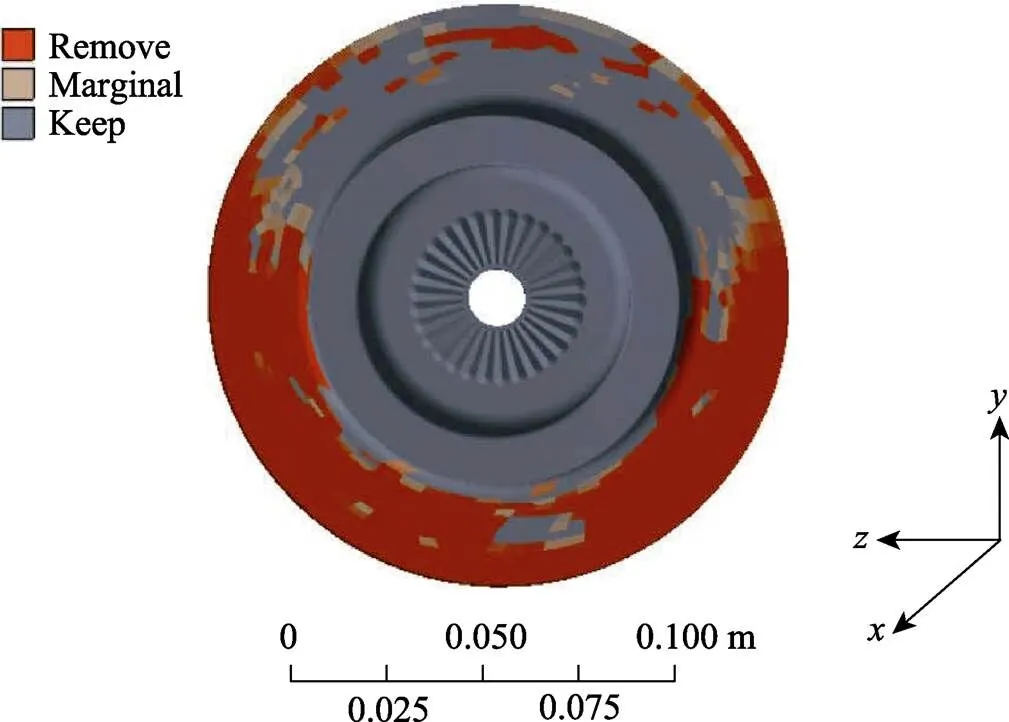
图9 材料缩减20%后形状优化云图
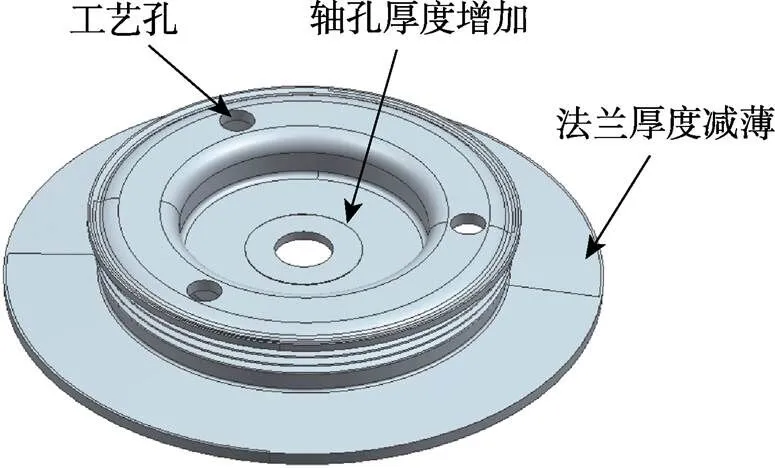
图10 改进后的三齿多楔轮结构
Fig.10 Three-tooth multi-wedge wheel structure after improvement
对改进后的三齿多楔轮进行了模拟测试,结果如图11所示,模型优化前后的数据见表1。从图11可以看出,最大变形和最大应力出现位置与修改前出现的位置基本一致,但最大应力值出现了明显下降,说明结构优化方案是合理可行的。另外,从表1可以看出,经过结构优化,零件质量减少了3.2%,刚度变化不大,最大等效应力值为34.902 MPa,强度得到增加。这说明在保证刚度的同时,不仅降低了零件质量,还增加了强度,也再次证明了优化方案的有效性。
表1 优化前后模型对比情况
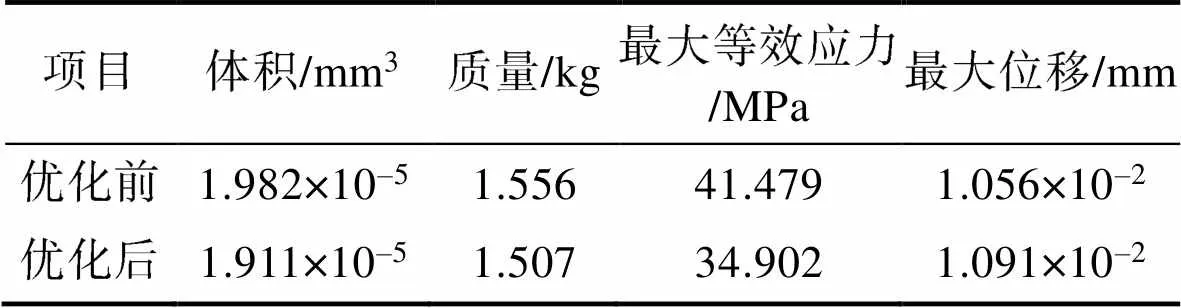
Tab.1 Comparison of models before and after optimization
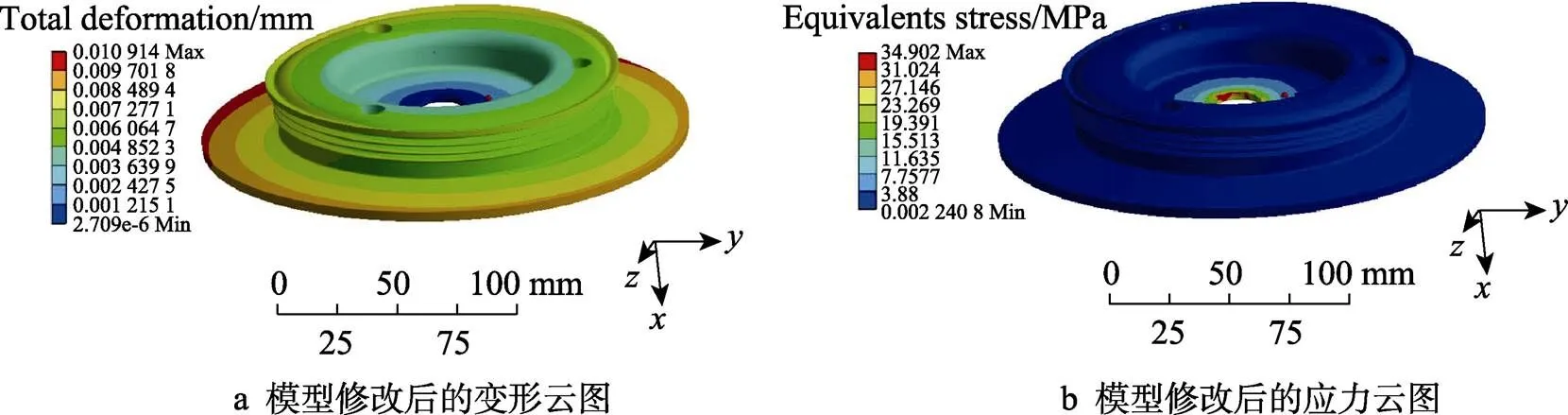
图11 三齿多楔轮结构优化后的静力学模拟结果
4 结论
1)随着齿数的增加,不同齿数带长法兰汽车多楔轮的最大变形量呈逐渐降低的趋势,最大变形均出现在多楔轮长法兰边缘位置。应力集中均出现在轴孔处,三齿带长法兰汽车多楔轮的最大应力值小于一齿带长法兰汽车多楔轮,约为41.48 MPa。
2)一齿、二齿结构带长法兰汽车多楔轮在三阶到四阶的固有频率增长速率大于三齿结构多楔轮,三齿结构带长法兰汽车多楔轮在四阶到五阶的固有频率增长速率大于一齿、二齿结构多楔轮。一齿、二齿和三齿结构带长法兰汽车多楔轮的固有频率分别为95.35~ 1721.20 Hz、65.33~1778.30 Hz和56.62~1691.90 Hz。不同齿数的带长法兰汽车多楔轮的固有频率范围基本一致。在相同载荷和约束作用下,三齿带长法兰汽车多楔轮具有较好的结构稳定性。
3)三齿结构带长法兰汽车多楔轮为最优结构,其振型主要为沿轴振动和绕轴方向的张合弯曲振动。结构优化后零件的质量减少了3.2%,刚度变化不大,强度增加。
[1] 吴玉程, 夏冲冲, 李明, 等. 多楔带轮旋压成形工艺及缺陷分析[J]. 塑性工程学报, 2016, 23(5): 57-61.
WU Yu-cheng, XIA Chong-chong, LI Ming, et al. Analysis of Spinning Process and Defects for Multi- Wedge Belt Pulley[J]. Journal of Plasticity Engineering, 2016, 23(5): 57-61.
[2] 夏冲冲. 多楔带轮旋压成形工艺及缺陷分析研究[D]. 合肥: 合肥工业大学, 2017: 1-10.
XIA Chong-chong. Study on Analysis of Multi-Wedge Belt Pulley Spinning Process and Defects[D]. Hefei: Hefei University of Technology, 2017: 1-10.
[3] 王成和, 刘克璋, 周路. 旋压技术[M]. 福州: 福建科学技术出版社, 2017: 2-33.
WANG Cheng-he, LIU Ke-zhang, ZHOU Lu. Spinning Technology[M]. Fuzhou: Fujian Science and Technology Press, 2017: 2-33.
[4] 李峰. 特种塑性成形理论及技术[M]. 北京: 北京大学出版社, 2011: 170-185.
LI Feng. Special Plastic Forming Theory and Technology[M]. Beijing: Peking University Press, 2011: 170-185.
[5] 解芳, 冯长虹, 王召兴, 等. 汽车发动机水泵带轮结构改进设计[J]. 机械强度, 2014, 36(2): 285-289.
XIE Fang, FENG Chang-hong, WANG Zhao-xing, et al. Improved Structure Design of Belt Wheel in Automobile Engine Water Pump[J]. Journal of Mechanical Strength, 2014, 36(2): 285-289.
[6] 陈思思. 汽车同步带齿形对传动噪声影响规律研究[D]. 长春: 长春工业大学, 2020: 28-62.
CHEN Si-si. Study on the Influence of Teeth Profile of Synchronous Belt on Transmission Noise[D]. Changchun: Changchun University of Technology, 2020: 28-62.
[7] 唐季平, 吴超, 代光旭, 等. 多楔带轮旋压增厚成形工艺有限元分析及试验研究[J]. 锻压技术, 2018, 43 (8): 97-102.
TANG Ji-ping, WU Chao, DAI Guang-xu, et al. Finite Element Analysis and Experimental Study on Spinning Thickening Forming Process of Multi-Wedge Pulley[J]. Forging & Stamping Technology, 2018, 43(8): 97-102.
[8] 李萍, 胡传鹏, 杨卫正, 等. 带横向外凸筋多楔轮旋压成形规律及工艺研究[J]. 哈尔滨工业大学学报, 2018, 50(11): 153-159.
LI Ping, HU Chuan-peng, YANG Wei-zheng, et al. Study on Spinning Forming Process of Multi-Wedge Belt Pulley with Transverse Outer Ribs[J]. Journal of Harbin Institute of Technology, 2018, 50(11): 153-159.
[9] 曹进, 周敏, 解贵华, 等. 基于数值模拟的多楔带轮成形工艺研究[J]. 锻造与冲压, 2020(6): 39-42.
CAO Jin, ZHOU Min, XIE Gui-hua, et al. Research on the Forming Process of Multi-Wedge Belt Wheel Based on Numerical Simulation[J]. Forging & Metalforming, 2020(6): 39-42.
[10] 刘志海, 杨永锋, 田绍鲁, 等. 基于ANSYS的六自由度机械臂静力学分析[J]. 煤矿机械, 2020, 41(12): 75- 77.
LIU Zhi-hai, YANG Yong-feng, TIAN Shao-lu, et al. Static Analysis of Six Degree of Freedom Mechanical Arm Based on ANSYS[J]. Coal Mine Machinery, 2020, 41(12): 75-77.
[11] PRADLWARTER H J, SCH UELLER G I. A Consistent Concept for High and Low Frequency Dynamics Based on Stochastic Modal Analysis[J]. Journal of Sound and Vibration, 2005, 88(3): 653-667.
[12] ZHOU Ya-dong, ZHANG Yi-le, ZENG Wei-li, et al. Fast Modification-Aimed Stress Modal Analysis of Thin Plates with Holes/Notches[J]. Engineering Structures, 2021, 238: 112248.
[13] 周炬, 苏金英. ANSYS Workbench有限元分析实例详解(动力学)[M]. 北京: 人民邮电出版社, 2019: 28-55.
ZHOU Ju, SU Jin-ying. Detailed Explanation of ANSYS Workbench Finite Element Analysis Example (Dynamics)[M]. Beijing: Posts& Telecom Press, 2019: 28-55.
[14] 陈鸣涧, 杨振宇, 李陆宽, 等. 某压载挂车车架静态特征与模态分析[J]. 机械设计与制造工程, 2020, 49 (12): 77-81.
CHEN Ming-jian, YANG Zhen-yu, LI Lu-kuan, et al. Static Characteristic and Modal Analysis of a Ballast Trailer Frame[J]. Machine Design and Manufacturing Engineering, 2020, 49(12): 77-81.
[15] 季文美, 方同, 陈松淇. 机械振动[M]. 北京: 科学出版社, 1985: 182-243.
JI Wen-mei, FANG Tong, CHEN Song-qi. Mechanical Vibration[M]. Beijing: Science Press, 1985: 182-243.
[16] 彭显昌, 蔡文奇, 林志斌, 等. 电动汽车变速箱壳体静动态分析及拓扑优化设计[J]. 机械传动, 2021, 45 (7): 74-81.
PENG Xian-chang, CAI Wen-qi, LIN Zhi-bin, et al. Static and Dynamic Analysis and Topological Optimization of Gearbox Housing in Electric Vehicle[J]. Journal of Mechanical Transmission, 2021, 45(7): 74-81.
[17] 张乐, 苗虹, 何启源, 等. 基于ANSYS的汽轮发电机定子绕组端部模态分析[J]. 重庆理工大学学报: 自然科学版, 2020, 34(9): 252-258.
ZHANG Le, MIAO Hong, HE Qi-yuan, et al. Modal Analysis of Stator Winding End of Turbogenerator Based on ANSYS[J]. Journal of Chongqing University of Technology: Natural Science, 2020, 34(9): 252-258.
[18] 黄观明, 杨宏亮, 张建波, 等. 基于Ansys的某型舰炮托架拓扑优化设计[J]. 舰船科学技术, 2018, 40(3): 142-145.
HUANG Guan-ming, YANG Hong-liang, ZHANG Jian- bo, et al. Topology Optimization Design of a Certain Type of Naval Gun Bracket Based on Ansys[J]. Ship Science and Technology, 2018, 40(3): 142-145.
[19] 张淑艳, 郭辉, 孙向轩. 电动汽车减速器箱体结构优化设计[J]. 机械设计与研究, 2013, 29(2): 133-136.
ZHANG Shu-yan, GUO Hui, SUN Xiang-xuan. Structure Optimization Design of Electric Vehicle Gear Box[J]. Machine Design & Research, 2013, 29(2): 133- 136.
Static and Dynamic Analysis and Structure Optimization of Automotive Multi-Wedge Wheel with Long Flange
ZHOU Jin-zhaoa, LIU Leia, WANG Zhao-yua, SHI Wen-chaob, LI Pinga, XUE Ke-mina
(a. School of Materials Science and Engineering; b. Industry and Equipment Technology Institute, Hefei University of Technology, Hefei 230009, China)
The work aims to study the structural stability of automotive multi-wedge wheel with long flange and realize the lightweight of parts by carrying out simulation study and optimization design of the multi-wedge wheel structure. The finite element model was established to conduct static and dynamic analysis on the automotive multi-wedge wheel with different tooth number structure by ANSYS finite software, so as to study the deformation, stress distribution law and change of inherent frequency. According to the simulation results, the first to sixth-order inherent frequencies ranged from 56.62 to 1691.90 Hz and the three-tooth structure was the optimal structure of the multi-wedge wheel, with good structural stability and high transmission efficiency. The excitation source should be avoided in the-axis and-axis directions in the actual working conditions, and the optimized structure of the three-tooth multi-wedge wheel reduces the mass by 3.2%, with the stiffness basically unchanged and the strength increased, which provides a certain reference value for the actual structural design of the automotive multi-wedge wheel.
multi-wedge wheel with long flange; modal analysis; static analysis; structural stability; structure optimization
10.3969/j.issn.1674-6457.2022.02.002
TG306
A
1674-6457(2022)02-0007-07
2022-01-05
大学生创新创业训练计划(201910359011);校企合作项目(W2017JSKF0090)
周金朝(1997—),男,硕士生,主要研究方向为材料成形过程与技术。
薛克敏(1963—),男,博士,教授,主要研究方向为精密塑性成形工艺与仿真。
