追踪及凝视状态下地气光对空间目标成像影响

张路平，肖山竹，胡谋法，陈盛

国防科技大学 电子科学学院, 长沙 410073

1 引言

地气光辐射是指以地球表面为下限、大气上界为上限的地球-大气系统向宇宙空间释放各类辐射的总称[1]。由于漫反射，地球大气层会将反射的太阳光辐射到探测器，对空间目标探测干扰较大，地气光已成为航天器远距离弱小目标探测最为严重的干扰因素。如何消减地气光对空间目标成像的影响成为当前空间弱小目标探测识别亟需解决的问题。

文献[2]建立了地气光对星敏感器的辐照度影响模型，但对地气光辐射强度变化规律及对星敏感器星提取精度的影响未定量研究。文献[3]在分析空间目标可见光相机探测原理时简单分析了宇宙深空背景噪声的影响。文献[4]对空间碎片经过南大西洋异常区[5](Southern atlantic anomaly, SAA区)时的探测影响因素进行了分析。文献[6]提出了一种利用姿态调整规避地气光的空间碎片探测方法，其实质是通过调节机械装置来规避地气光辐射。文献[7]将地气光辐射对天基可见目标观测的影响量化为相机的离轴角约束，从而避开地气光辐射。文献[8]对不同季节的地气光辐射变化进行了分析，文献[9]将地气光辐射作为空间目标的辅助照明光源进行研究。上述研究在对地气光辐射建模时，并没有定量分析其对空间目标成像的影响。

分析地气光辐射对空间目标成像的影响成为开展地气光背景抑制研究的基础。本文将空间目标与地气光辐射统一构建在同一场景，利用STK在不同轨道探测平台上设计不同的探测方式对同一空间目标进行仿真，在目标进入地气光辐射的强干扰时段，采用微元法建立空间目标及地气光辐射模型，定量分析不同探测平台不同探测器场景下地气光辐射对空间成像目标信噪比的影响，得到目标SNR的变化规律，为消减地气光辐射影响和开展空间目标检测提供门限阈值参考，为天基光电系统空间目标探测方式选择提供参考。

2 地气光对空间目标成像影响模型

2.1 目标辐射模型

目标辐射能量主要来自于太阳光辐照，根据普朗克方程太阳光在一定光谱段范围的辐射强度为：

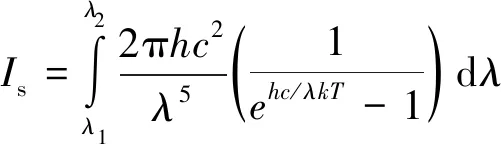
(1)

式中：h，c，k分别为普朗克常数、光速、玻尔兹曼常数；λ2和λ1为探测器可探测光谱的上下限波长；T为太阳黑体温度。空间目标表面接收到太阳光的辐射照度为：

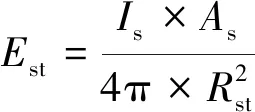
(2)

式中：As为太阳表面积；Rst为太阳与空间目标的距离。将空间目标看作成一个朗伯辐射体，探测器接收到空间目标的辐射强度为：

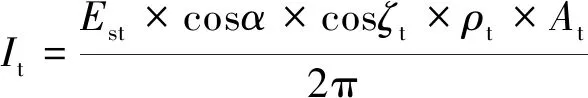
(3)

式中：α为太阳光与空间目标、探测器之间形成的探测相角；ζt为空间目标探测连线与探测器光轴的夹角，即目标离轴角；ρt为空间目标反射率；At为空间目标等效截面积。将目标信号能量转化为光子数，则进入探测器的目标信号光子流量密度为：

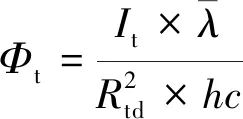
(4)

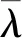
mt=-2.5log [Φt/(5×1010)]

(5)

2.2 地气光辐射模型

地气光辐射对空间目标成像的影响是通过增加地气光背景噪声从而改变目标信噪比实现的[10]。假定太阳到地球大气层表面的距离为Rse，结合公式(1)，则太阳对地球大气层表面的辐射照度为：

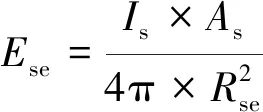
(6)

将地球看作是一个朗伯球体，它将地气光辐射到探测器。追踪与凝视探测器的探测光路如图1所示。图中：β为太阳光到大气层表面面元的连线与面元法线的夹角，即光照角；θ为面光源对探测器投射光方向与地气光辐射面元法线的夹角，即出射角；ζe为面光源对探测器投射光方向与探测器光轴方向的夹角，即离轴角。追踪探测器主动追踪空间目标，其视线光轴始终对准目标，凝视探测器凝视地球上空某一区域，其视线光轴始终对准地球。

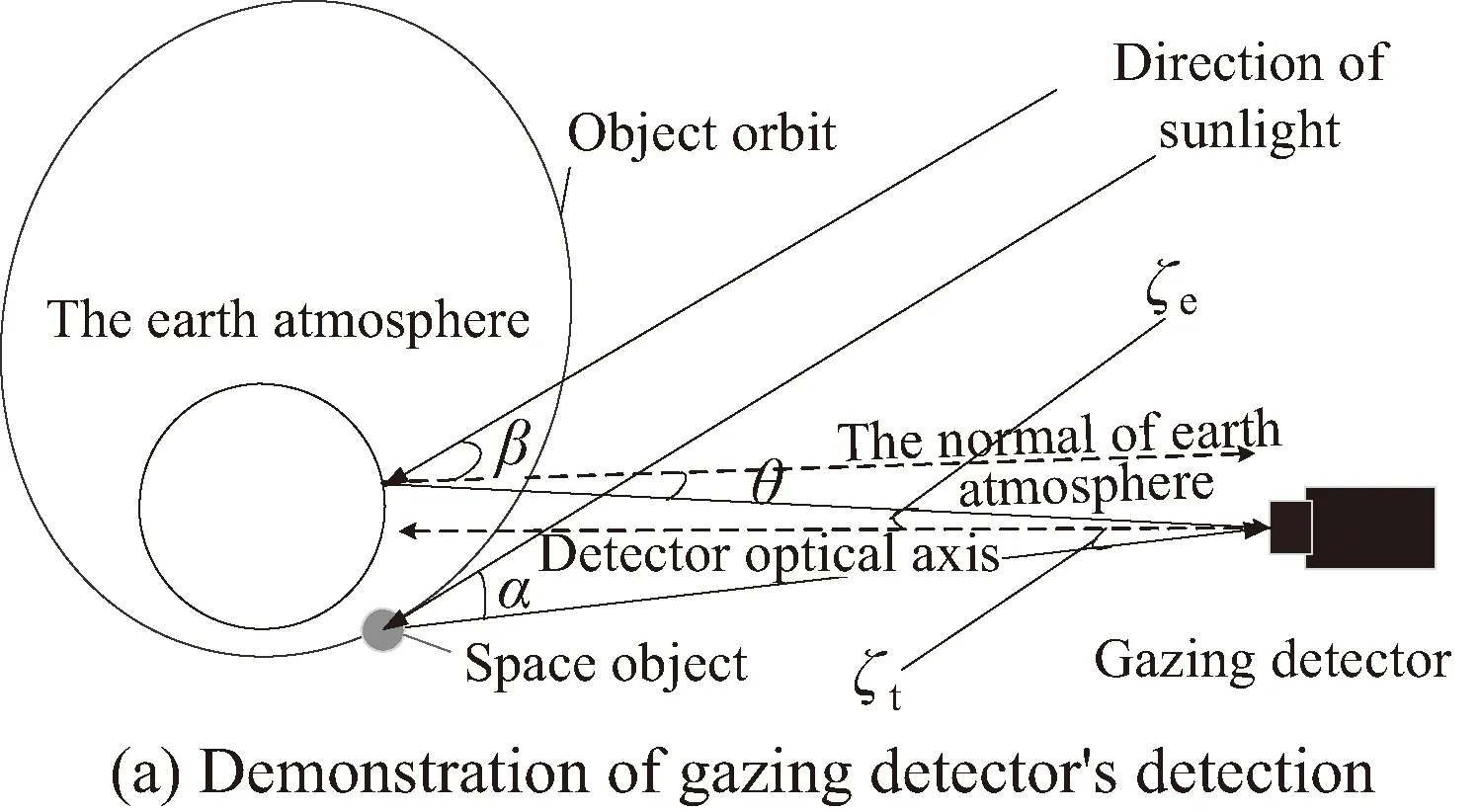
图1 不同探测器探测示意图Fig.1 Demonstration of detecting with different detectors

采用微元法分析地气光辐射模型。太阳光照射到地球表面某一区域内，将该区域分成尽可能多的微小面元，每一块微小面光源产生的辐射强度为：

(7)

式中：ρe为地球表面反射率。假定进入探测器的地气光辐射区域总面积为Ae，地气光与探测器之间的距离为Red，则探测器接收到的地气光辐射照度为：

(8)

根据地气光辐照度与等效星等之间的关系[11-13]，可得地气光辐射等效星等me为：

me=log2.512(E0/Eed)

(9)

式中：E0=2.96×10-8W/m2为0星等目标在地球大气层外产生的辐射照度。

2.3 空间目标成像信噪比

探测器可能接收到的噪声[14-16]包括目标辐射光子噪声nt、背景噪声ne、暗电流噪声nd、电子读出噪声nr，其中：

(10)

式中：Nt、Ne、Nd分别为目标辐射光电子数、地气光背景噪声光电子数、探测器暗电流噪声光电子数。结合公式(2)、(3)、(4)，可得探测器接收到的目标光子数Nt为：

Nt=Φt·Ad·τ·Q·t/np

(11)

式中：Ad、τ分别为光学系统的有效入瞳面积、透过率；Q为探测器的量子效率，t为信号曝光时间，np为空间目标成像总像素数。探测器接收到的地气光背景噪声光子数Ne为：

Ne=Φe·Ad·τ·Ap·Q·t

(12)

式中：Φe=5×1010/2.512me，为单位立体角地气光背景光子流量密度，Ap为探测器单个像元的角面积。联立公式(6)、(7)、(8)、(9)、(12)得地气光辐射产生的光子数Ne如下式：

(13)

由于各噪声相互独立，由公式(10)、(11)、(13)得到，探测器接收到总的光子噪声方差为所有噪声方差之和：

则空间目标成像信噪比SNR为：

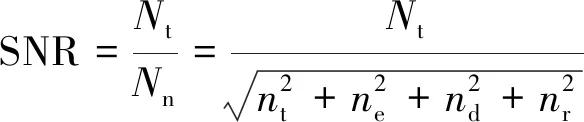
(14)

3 地气光对空间目标成像信噪比影响仿真分析

3.1 探测及目标运动场景设计

利用STK对探测及目标运动场景进行仿真[17]。探测平台为GEO与MEO卫星上搭载的追踪及凝视可见光探测器，探测对象为HEO轨道上逆时针运动的卫星目标，其轨道参数如表1所示。部分探测器参数参照了美国“空间中段监视”试验卫星上搭载的天基可见光相机参数，GEO与MEO平台上探测器瞬时视场分别为3.52 arcsec/pixel、21.09 arcsec/pixel，目标等效球体半径为2 m，表面反射率为0.33。探测器主要参数如表2所示。

表1 各轨道参数Table 1 Parameters of orbits

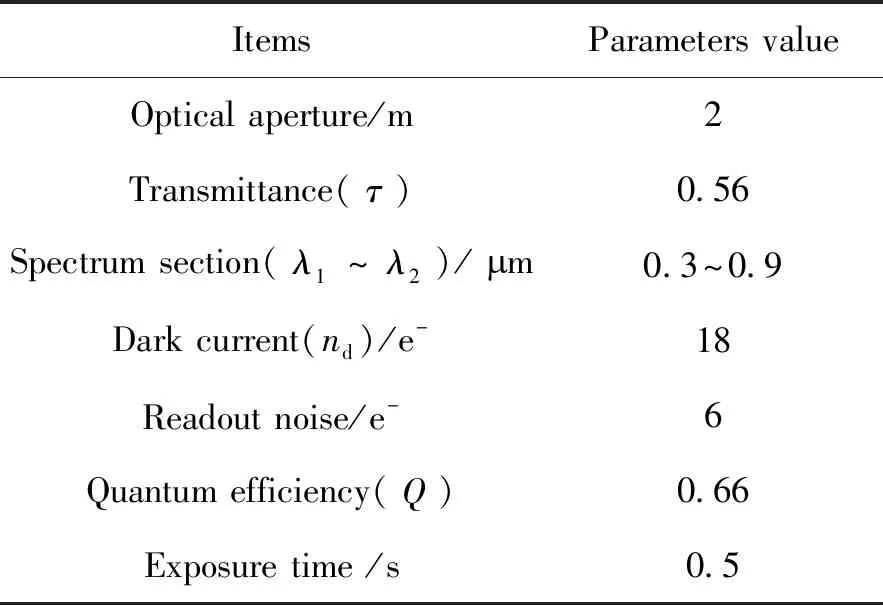
表2 成像系统参数Table 2 Parameters of imaging system

根据上表，设置STK场景参数，可得到GEO、MEO探测平台及HEO轨道目标及太阳在J2000地球惯性坐标系下的实时空间坐标。STK仿真场景如图2所示，在图2(a)中，地球表面白亮区域为太阳照射区域，黄色圆锥部分与品红色圆锥部分分别为凝视探测器与追踪探测器视场；图2(c)中黄线区域内为凝视探测器视线中的地气光背景区域，品红色部分为追踪探测器视线中的地气光背景区域，红线为晨昏线；图2(b)中粉色圆锥部分与紫色圆锥部分分别为凝视探测器与追踪探测器视场；图2(d)中粉色区域与紫色区域分别为凝视探测器与追踪探测器视线中的地气光背景区域。

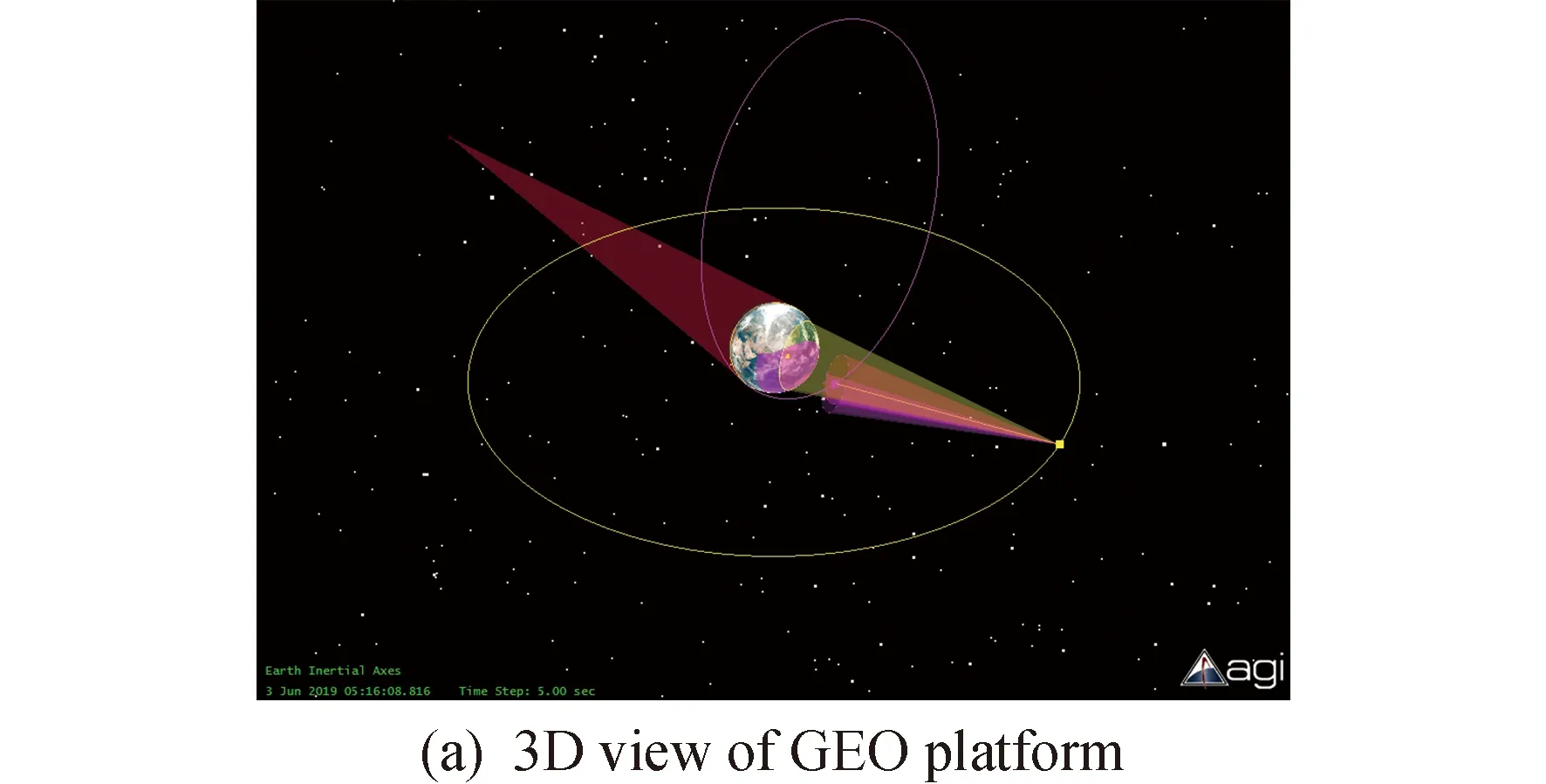
图2 GEO及MEO平台探测场景视图Fig.2 Views of GEO and MEO platform detection scene

3.2 不同探测器空间目标成像特性分析

在一个HEO轨道目标运动周期内，将目标及地气光辐射同时进入至同时离开探测器视场的时段称为一次完整探测时段。综合考虑目标可探测条件及地气光辐射进入探测器视场的时间段，选择的探测日期为2019年6月3日。表3为GEO与MEO平台探测器在该探测日期内的完整探测时段。

表3 不同探测器探测时段Table 3 Detection periods of difference detectors

追踪探测器始终瞄准目标，凝视探测器始终瞄准地球某一固定区域。场景中，凝视探测器完整探测时段均包含在追踪探测器完整探测时段内。故选择凝视探测器的完整探测时段作为采样时段，采样间隔为1 s。

(1)不同探测平台上目标等效星等变化

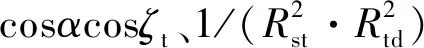
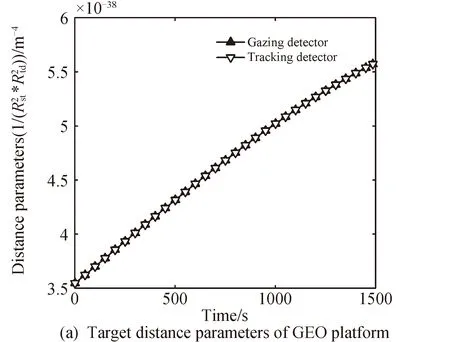
图3 不同探测平台上目标参数及等效星等变化Fig.3 Variation of target parameters and equivalent magnitude on different detection platform

采样时段内，HEO轨道目标从南极上空经赤道上空向远地点运动，目标距离GEO探测平台和太阳越来越近，Rst与Rtd逐渐减小。目标探测相角α从44°逐渐增至54°，追踪探测器目标离轴角ζt始终为0，凝视探测器目标离轴角ζt从7.5°减小到2.7°，再增加到7.5°。综合距离参数和角度参数的影响，GEO平台上两个探测器得到的成像目标信号强度逐渐增强，由公式(5)得到目标等效星等逐渐减小。

在完整探测时段内，HEO轨道目标距离MEO探测平台与太阳越来越近，故Rst与Rtd逐渐减小。MEO探测平台目标探测相角α从16°增至58°，追踪探测器ζt始终为0，凝视探测器ζt从24.0°减小到6.3°,再增加到24.0°。综合距离参数和角度参数的影响，MEO平台两个探测器得到的成像目标信号强度先增后减，则目标等效星等先减后增。

MEO探测平台的距离参数、目标探测相角α、目标离轴角ζt的变化均比GEO探测平台大，故其探测得到的目标信号变化比GEO探测平台大；且MEO探测平台的Rtd约为GEO探测平台的Rtd的四分之一，故其目标等效星等比GEO探测平台更小。

(2)不同探测平台上地气光等效星等变化

完整观测时段内地气光辐射参数及等效星等变化如图4所示。

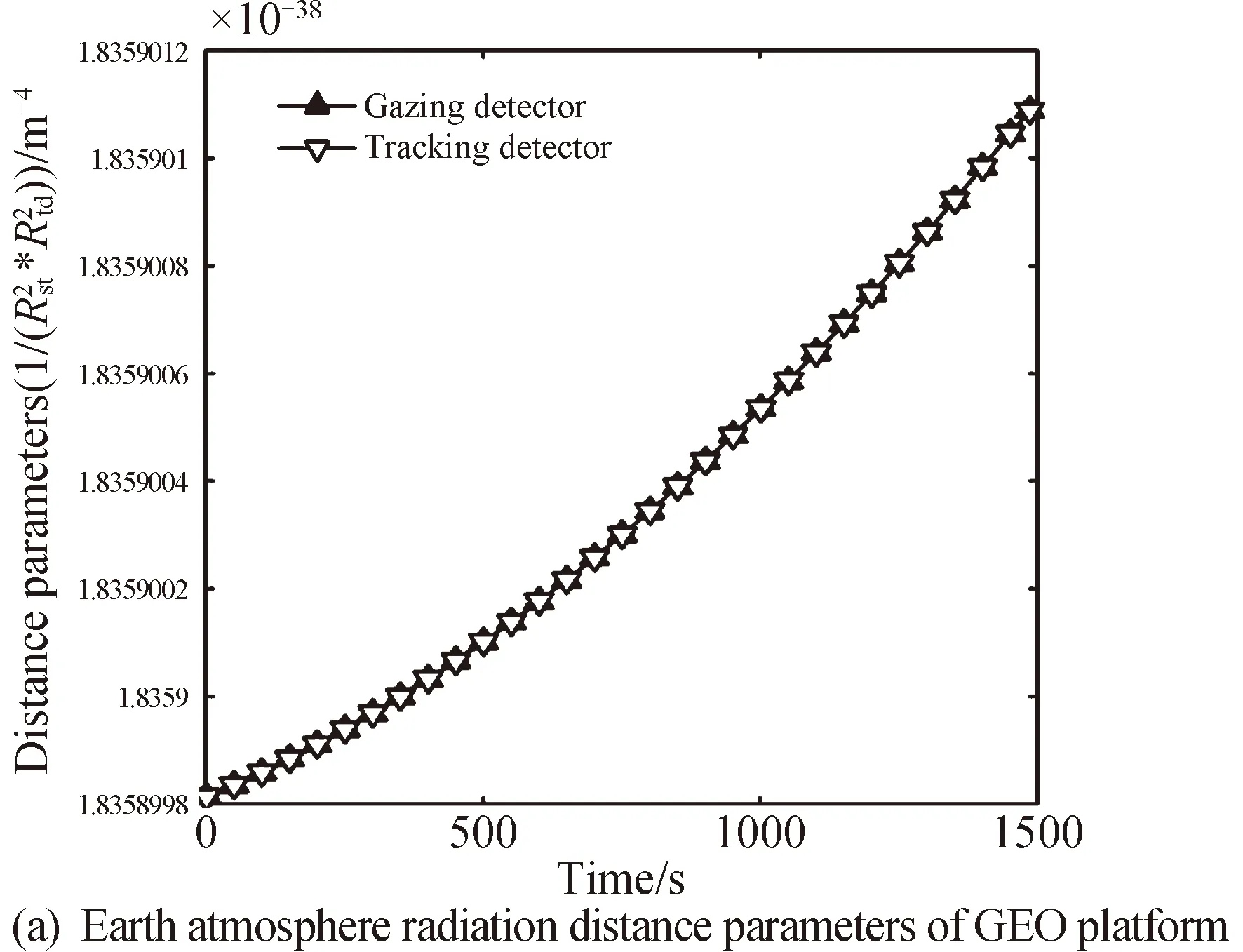
图4 不同探测平台上地气光辐射参数及等效星等变化Fig.4 Variation of earth atmosphere radiation parameter and equivalent magnitude on different detection platforms

在完整探测时段内，GEO/MEO探测平台上凝视探测器光轴始终对准地球某一区域，GEO探测平台Red不变，Rse逐渐变小，MEO探测平台Red变化很小，Rse逐渐变小。GEO探测平台地气光辐射光照角β从44.0°增至49.2°，出射角θ为0，凝视探测器ζe为0，追踪探测器ζe从7.5°减至2.7°,再增至7.5°，相对于β的余弦变化，ζe的余弦变化很小，对距离参数影响小。MEO探测平台上地气光辐射光照角β从31.9°增加到42.4°，出射角θ为0，凝视探测器地气光辐射离轴角ζe为0，追踪探测器地气光辐射离轴角ζe先从24.0°减至6.3°，再增至24.0°。由公式(6)、(7)、(8)得到，GEO平台上两个探测器的地气光辐射强度均逐渐减小，而MEO平台上凝视探测器地气光辐射强度逐渐减小，追踪探测器地气光辐射强度先增加后减小，由公式(9)得到其等效星等变化如图4(e)、图4(f)所示。

MEO探测平台的距离参数、角度参数变化均比GEO探测平台大，故其探测得到的地气光辐射背景信号变化比GEO探测平台大；且MEO轨道高度比GEO轨道小得多，导致MEO探测平台的距离参数比GEO探测平台大，从而使得其地气光等效星等更小。即MEO探测平台的检测性能强于GEO探测平台。

(3)不同探测平台上空间目标成像信噪比变化

完整探测时段内不同探测平台不同探测器探测得到的空间目标成像信噪比由公式(14)可得，其变化如图5所示。

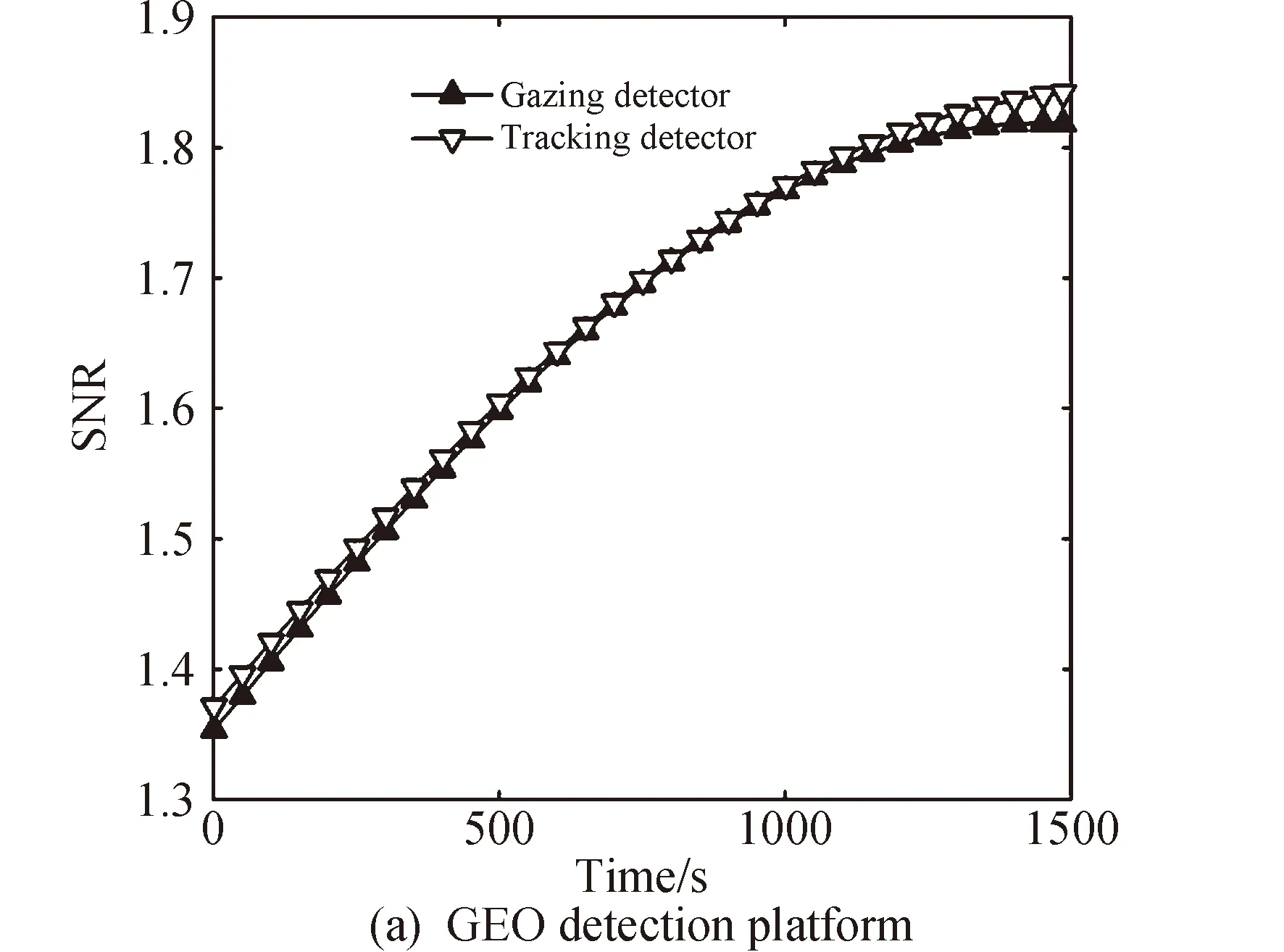
图5 不同探测平台不同探测器目标信噪比Fig.5 The target SNR of different detectors on different detection platforms

GEO探测平台上两个探测器探测得到的目标信号逐渐增强，地气光辐射信号逐渐减弱，空间成像目标信噪比逐渐增大。MEO探测平台上两个探测器探测得到的目标信号先增后减，凝视探测器地气光辐射信号逐渐减弱，追踪探测器地气光辐射信号先增后减，但地气光辐射信号变化小于目标信号变化，故而空间成像目标信噪比先增后减。

同一探测平台上追踪探测器目标信噪比大于凝视探测器，这主要由目标离轴角与地气光辐射离轴角的不同引起的。以GEO探测平台为例，当空间目标进出探测器视场时，凝视探测器目标离轴角为7.5°，其地气光辐射离轴角为0；而此时追踪探测器目标离轴角为0，其地气光辐射离轴角为最大值7.5°，故追踪探测器空间成像目标信噪比高于凝视探测器。GEO探测平台上二者由于轨道较高信噪比最大相差仅0.03，而MEO探测平台轨道仅为GEO轨道的四分之一，该平台二者信噪比最大相差可达0.55；根据弱小目标检测信噪比与检测率之间的分析研究[18]，GEO平台追踪探测器相比凝视探测器的目标检测概率最大可提高0.47%，而MEO平台上追踪探测器相比凝视探测器的目标检测概率最大可以提高4.19%。

3.3 模型验证

空间目标及地气光辐射等效星等模型是本文研究的基础。陈荣利等利用普森公式建立空间目标辐照模型，并将该模型计算结果与紫金山天文台及国家天文台兴隆站观测的实测数据进行比对，二者仅存在0.5个星等误差[11]。虽然未能直接用实测数据验证本文模型的正确性与合理性，但可与基于普森公式模型的计算结果进行比对，从而间接验证与实测数据的差异。

将本文建模所用的目标反射率(即ρt)、目标等效直径(4 m)、目标探测距离(即Rtd)、位相角等参数代入普森公式可计算出基于该模型的空间目标等效星等，同时与本文模型得到的空间目标等效星等进行对比，对比结果如表4所示。

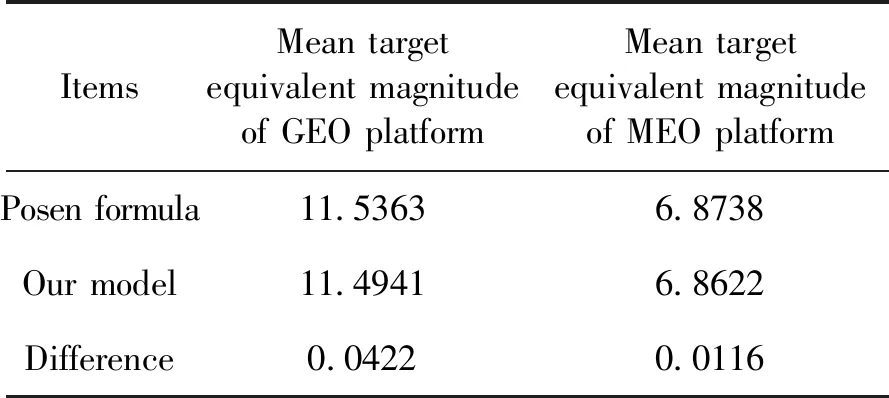
表4 两种模型等效星等均值Table 4 Mean value of equivalent magnitude of two models

表4结果表明，由于目标探测距离与位相角参数取值的有效位数误差，本文模型计算得到的GEO平台与MEO平台探测到HEO轨道目标的等效星等与基于普森公式计算得到的等效星等均值仅有0.05个星等以内的差异。两种模型计算结果表明本文模型得到的目标等效星等与真实观测数据星等吻合，构建的空间目标等效星等模型正确合理。

本文主要关注在GEO平台上探测目标时，地气光辐射对空间目标成像的影响，将空间目标与地气光辐射统一构建在同一场景而非孤立构建等效星等模型，进而得到观测时段内的空间目标成像信噪比变化。上述研究成果为地气光辐射建模提供了理论支撑，确保模型合理正确。

4 结论

空间目标进入地气光背景后可能会被地气光噪声吞没，造成空间目标丢失，因此，需要对空间目标进入地气光背景后的成像规律进行研究。本文将空间目标与地气光辐射统一在同一场景中，为分析空间目标在地气光强干扰下的成像特性提供了翔实的实验数据参考，适用于可见光探测器对各类飞行器在地气光干扰下的成像仿真，为研究远距离空间目标检测识别提供理论基础。下一步，可通过对空间目标形状、运动模型进行更为细致的建模，得到更贴合实际场景空间目标的成像特性数据。