基于特征匹配的三维点云粗配准方法

郭克凡,王威娜,林 楷

(1.吉林化工学院 信息与控制工程学院，吉林 吉林 132022；2.吉林化工学院 理学院，吉林 吉林 132022；3.苏州迈为科技股份有限公司,江苏 苏州 215200)

随着激光雷达和扫描设备的不断升级，所需要的三维信息以更低的成本和更短的时间获取[1]，三维重构技术的应用也随之越来越广泛.三维点云配准是三维重构技术中的关键一环，一个良好的配准结果对三维重构的效果起着决定性的作用.从最经典的点云配准算法—迭代最近点(Iterative Closest Point，ICP)[2]到后来的ICP改进算法[3]，可以发现，为了保证此类算法的精确性，通常需要对点云进行粗配准，以获得良好的初值.

在粗配准算法中，较为主流的是基于主成分分析(Principal Component Analysis,PCA)[4]及其改进方法对点云信息进行变换估计.Chung等[5]估计激光雷达采集信息点主轴方向，利用PCA算法计算出多站点云的协方差矩阵，进而求出旋转矩阵与平移向量.Rusu等[6]提出著名的点特征描述子(Point Feature Histogram,PFH)计算不同视角点云的特征相似度，再求解刚性变换参数，此算法鲁棒性较低，易受噪声与离群点影响.Sun等[7]利用区域曲率图(Regional Curvature Maps，RCM)对三维点云的局部特征进行描述，将RCM子区域作为待配准点云的对应特征依据，利用几何一致性实现粗配准，该方法在一定程度上提升了配准精度.Fischler等[8]提出基于随机抽样一致算法(Random Samle Consensus,RANSAC)框架的方法，利用点云数据的重叠区域寻找特征点，进而计算刚性变换参数，该算法利用重复选择的方式寻找最优解，但由于其简单的利用概率作为约束条件，造成算法稳定性较低的缺陷，在含有噪声的环境中易产生误匹配.陶海跻等[9]利用RANSAC与特征直方图融合的方式，根据局部法向量选取点云数据的信息点，建立几何特征直方图后筛选对应配准点，再通过RANSAC算法对不同视角点云进行约束，求解旋转矩阵与平移向量.此算法大幅提升了配准的有效性，但当点云信息不明显或点云密度降低时，算法性能易受到影响.

根据以上的研究，提出一种基于特征匹配的三维点云粗配准算法.该算法根据源点云与目标点云的法向量变化程度选取特征点集并对特征点集中的点建立特征直方图，然后利用特征直方图获取相匹配的点对，根据刚性不变原则和RANSAC算法消除误配准的点对，求解出刚性变换参数.为了提升算法效率，加入了特征保留权值δ，通过对特征保留权值δ的设定，提高了算法的配准效率.算法流程如图1所示.

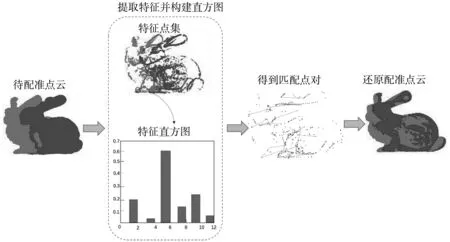
图1 算法流程图

1 基于特征匹配的三维点云粗配准

1.1 特征点集的选取

在基于特征匹配的点云配准中，为达到快速有效配准的目的，首先要选取特征点集.对于点集的特征描述采用法向量的方法，通过对点云法向量的求解可以发现：在点云的不同区域内，法向量有着不同程度的变化，如图2所示.图2(a)所示区域点的法向量变化程度不大，相对平缓；图2(b)所示区域点的法向量变化程度相对较大.

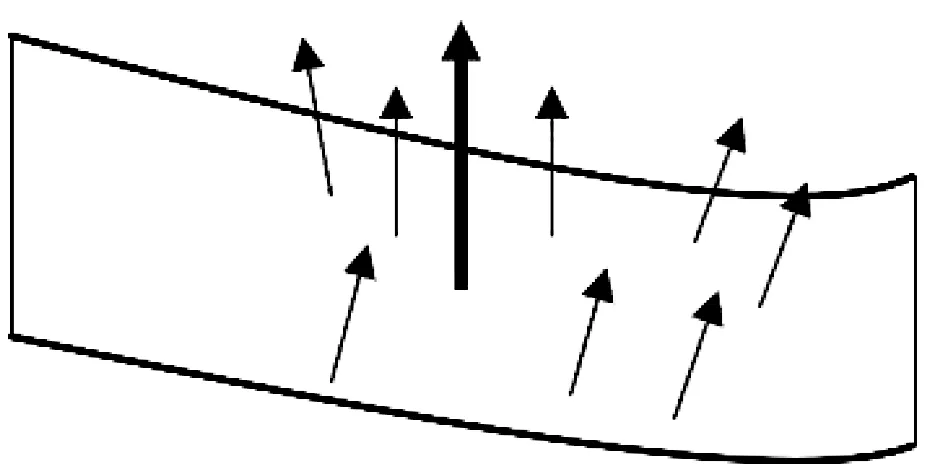
(a) 平坦曲面法向量

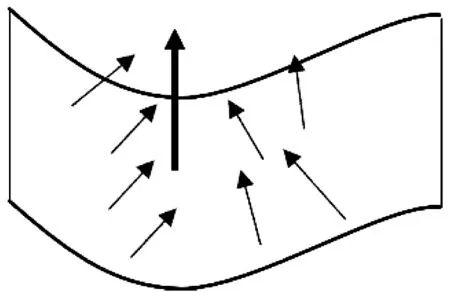
(b) 凹凸曲面法向量图2 不同区域的法向量

选取区域内法向量变化较大的点为特征点，可以更好地表现点云的面特征，具有较高的区分度，便于找到相匹配的点.特征度用该点的法向量与其邻域内其他信息点的法向量夹角的均值表示，即：

(1)

其中h为点pi的近邻点个数；αij表示点pi的法向量与其近邻点pj的法向量的夹角.为了提高算法的效率，加入特征保留权值δ来进行调整特征度，定义为：

(2)

根据上面对特征度的定义可以看出：特征度的大小与区域内起伏变化的程度成正比关系，因此点云中的特征点选取可根据定义的特征度来完成.为了减少后续的计算量，引入阈值o1将点云中起伏变化不明显的部分去除掉，即保留下来的初始特征点均满足fj>o1，对于保留下来的初始特征点中任意点pm，如果满足：

f(pm)=max[f(pm1),f(pm2),…,f(pm)] ，

(3)

则将初始特征点pm视为特征点，其中f(pm)为特征点pm在邻域内其他近邻点的特征度.将需要配准的点云中的源点云设为点云P，目标点云设为点云Q，根据提出的方法，分别对目标点云P和源点云Q的特征点进行提取，得到的特征点集分别为Pt={pt1,pt2,pt3,…,ptm′}、Qt={qt1,qt2,qt3,…,qtn′}，其中m′为源点云P的特征点个数，n′为目标点云Q的特征点个数.

1.2 建立特征直方图

待配准的两片点云通常不具有相同的空间结构关系，其稀疏程度也不相同，而且点云当中可能还会存在噪声，所以将夹角作为特征量的方法[10-11]在实际应用的场景当中描述的特征信息相对较少，不容易区分特征点使得无法达到理想的效果.为解决不容易区分特征点的问题，采用特征直方图的方法，利用特征直方图将特征点及其邻域内其他特性进行统计，并将特征点及其邻域内的几何特征采用特征向量的方式进行描述.

在以往的算法中，描述点云特征多为单一的特征值，并且这些特征值往往都较为接近，因此使点云当中一些特征变化不明显的点无法被有效地区分.基于上述分析，在描述点云方面使用特征直方图的方法，可描述更多的特征信息，便于区分不同特征的点云.提出的特征直方图方法如下：

1.在源点云P中任取一点pti，将pti视为球心，以r为半径构建球域，把球内的所有区域看作是pti的近邻域，因此，球内的所有点都是pti的近邻点记作N(pti)，如图3所示.

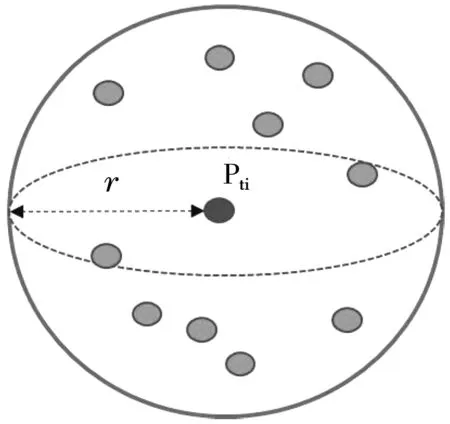
图3 N(pti)示意图

2.根据点Pti和N(Pti)的关系，选取以下3个空间特征：

f1=acos ，

(4)

f2= ，

(5)

f3=‖sh-pti‖ ，

(6)

在上述公式中，ni代表点pti的法向量；vk代表点pti某一近邻点的法向量；sk代表点pti某个近邻点的三维空间坐标.f1表示pti的法向量与它某一近邻点法向量之间的夹角，并且夹角通常在[0-π/2]区间内，所以将f1描述为4个区间，分别是0-π/6、π/6-π/3、π/3-π/2、π/2-π.f2代表pti的法向量与其邻域内某一点的点间向量的点积，根据点积值的正负，将f2分成两个部分.f3代表pti和其某一近邻点之间的欧式距离，选择r/4、r/2、3r/4这3个阈值，将f3分成4个部分.根据f1、f2、f3的划分，可构建一个4×2×4=32维的三维点云特征描述直方图.

3.确定特征点及其邻域内其他信息点在特征直方图中的位置.根据“2.”中得到的结果，f1的值在0-π/6、π/6-π/3、π/3-π/2、π/2-π内分别记作1、2、3、4；根据f2的正负，将f2记作0和1，如果f2为负数，将f2记作1，否则记作0；r/4、r/2、3r/4将f3划分为0-r/4、r/4-r/2、r/2-3r/4和3r/4-r4个区间，f3的值在这3个区间内分别记作1、2、3、4.

fidex=k1+k2×4+k3×2 ，

(7)

从式(7)可以看出，fidex的结果可以得到点pti在特征直方图的具体位置，按照此过程遍历pti邻域内所有点，得到落入直方图不同位置的数量，然后除以邻域内点的总数，便可获得点pti的特征向量.按照此方法分别对源点云P和目标点云Q中的所有特征点建立特征向量.

1.3 初始匹配点对数组的获取

根据1.2节中建立的特征向量，在Pt和Qt中寻找特征相同或者相近的点，把它们看作匹配点对.在相似特征点的区分上，将特征向量之间的欧式距离作为衡量标准.因为点云存在不重叠的部分，所以在Pt和Qt中存在无法匹配的点，因此要设置一个阈值o2，去除掉欧式距离大于o2的误匹配点对，将筛选后的点对视为初始匹配点对，记作

(8)

其中num(SMatchdots)是匹配点对的数量.

1.4 精确匹配点对数组的获取

点云数据集中通常存在很多相似的点对，所以单纯的依靠欧式距离筛选出的匹配点对往往存在较大的误差，因此需采用其他方法在得到初始匹配点集的基础上筛选出正确的匹配点对.

将刚性不变约束条件与自适应的RANSAC算法相结合，从初始匹配点集中筛选出正确的匹配点对.在初始匹配点对中的任意两个点对(si1,si2)和(sj1,sj2)，如果他们的匹配关系都是正确的，根据刚性不变性可以得到dist(si1,si2) =dist(sj1,sj2)，因为在两个点云当中很难找出对应关系百分百正确的点对，所以正确匹配点对只需满足dist(si1,si2)≈dist(sj1,sj2).因为是近似关系，所以要设置合适的非负阈值o3，确保筛选出的点对可以满足配准要求.则SMatchdots中一个点对(sj1,sj2)满足下式：

(9)

则将点对(sj1,sj2)记为相对于点对(si1,si2)的符合距离约束的点对.

1.5 计算配准参数

根据1.4节中获得的正确匹配点集，运用四元素法[12]计算获得初始配准参数，旋转矩阵R和平移向量t.根据

(10)

综上所述，基于特征匹配的三维点云粗配准的算法描述为：

步骤1：计算点云的特征度.

将输入的源点云P和目标点云Q根据公式(2)计算其点云数据的特征度.

步骤2：筛选特征信息点.

选择适当的保留参数，对特征度大于保留参数的信息点作为源点云与目标点云中信息变化程度较好的特征点云.

步骤3：建立特征直方图并且构建初始对应关系.

依次将点云P、Q中的信息点p作为球心做一个半径为r的球形点云包围盒，根据公式(3)的描述将信息点与包围盒内的特征关系构建特征直方图.对比直方图的相同程度筛选出点云的对应关系.

步骤4：利用刚性不变约束以及RANSAC算法求解粗配准特征点对.

由于相同模型的源点云与目标点云的变换是刚性变换，所以可以使用刚性不变性约束步骤3中匹配点的对应关系，并利用RANSAC方法验证其准确性，得到满足要求的信息点之间的对应关系.

步骤5：求解对应点之间的配准参数.

利用四元素法根据公式(10)求解目标点云与源点云之间刚性变换的旋转矩阵R和平移向量t.

2 实验结果分析

2.1 实验设置及评价指标

为了验证提出算法的有效性，采用Standford 3d Scanning Repository[13]的Bunny、Dragon、Happy以及Armadillo模型进行配准效果测试.实验在Matlab软件2020a环境下运行于Intel(R) Core(TM) i5-8250U CPU，4G内存，Windows10的计算机上.实验中的参数设置为：h=15，o1=5，o2=0.05，o3=0.02.

实验采用旋转误差eR、平移误差et以及配准所需时间T这3种常用指标作为评价标准.这3种评价指标分别从配准的有效性和配准的效率两方面进行评价，并且都是数值越小所表示的性能越好.旋转误差eR和平移误差et的计算公式为：

(11)

et=‖tm-tg‖2，

(12)

其中，Rg和tg分别代表配准所需的旋转矩阵R和平移向量t的真值；Rm和tm则分别代表所求得的旋转矩阵R和平移向量t.

2.2 特征保留权值的确定

采用Bunny和Dragon两个模型进行实验，确定δ的取值.通过选用不同的特征保留权值δ，经过筛选后的特征保留点和配准结果如图4所示.

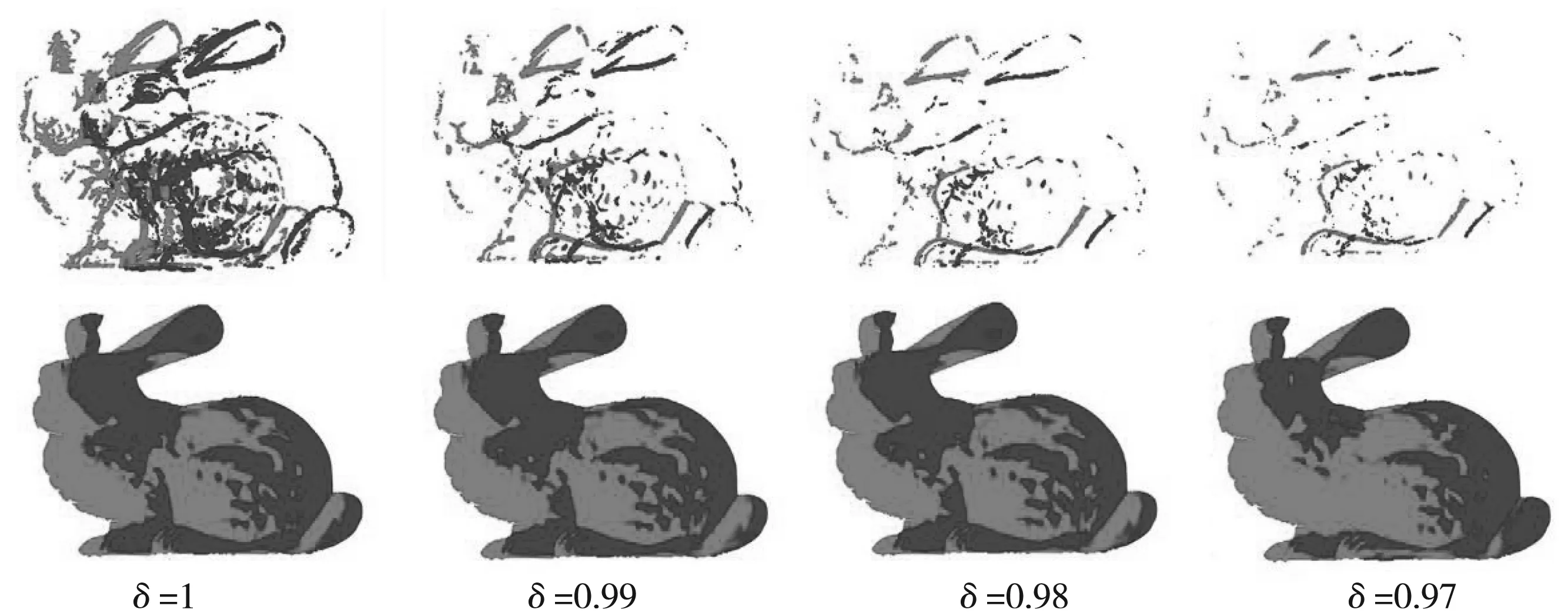
(a) Bunny保留点与配准结果

(b) Dragon保留点与配准结果图4 不同权值下配准结果对比

从实验结果可以看出，当特征保留权值δ分别取值1、0.99、0.98、0.97时，保留下来的特征点有较大差距，但是仍然有着较高的配准精度.δ取值越小保留下的特征点越少，减少数据量可以有效地缩短点云配准时间，提高配准的效率.为了更明显地体现实验结果，表1展示了不同权值下点云配准所需要的时间.

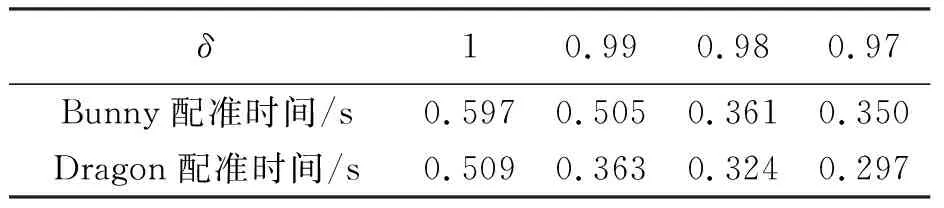
表1 不同权值下配准所需时间

从表1可以看出随着特征保留权值的减少，配准的效率也随之提高.Bunny模型配准时间从0.597降至0.350 s，Dragon模型配准时间从0.509降至0.297 s.所以配准效率随之特征保留权值的减小而提高，但是考虑精度的要求，因此特征保留权值不可以设置过低，特征保留权值取0.97，这样在保证了配准结果精度的同时，也提高了配准的效率.

2.3 配准实验结果分析

为了验证提出算法的有效性，采用Standford 3d Scanning Repository的Bunny、Dragon、Happy以及Armadillo模型进行配准效果测试，如图5所示.图5表明提出的算法可以有效地对这4个模型进行粗配准，并获得最优的配准结果.为了更加直观地表现该方法的有效性，实验结果的具体数值如表2～4所示.

图5 不同模型配准前后对比

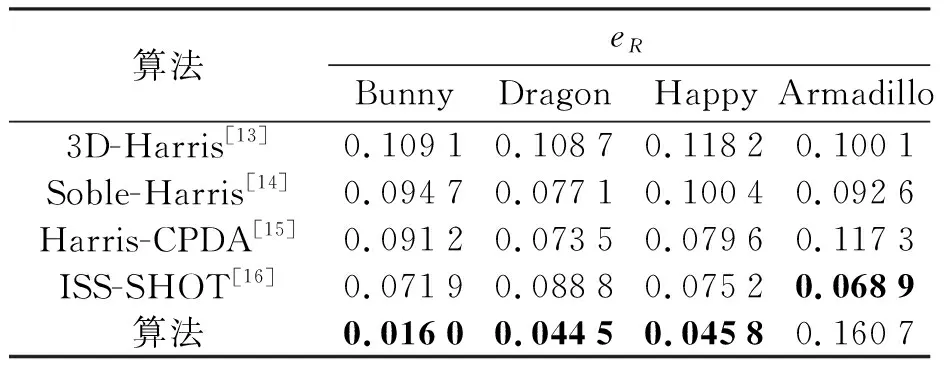
表2 粗配准算法的eR对比

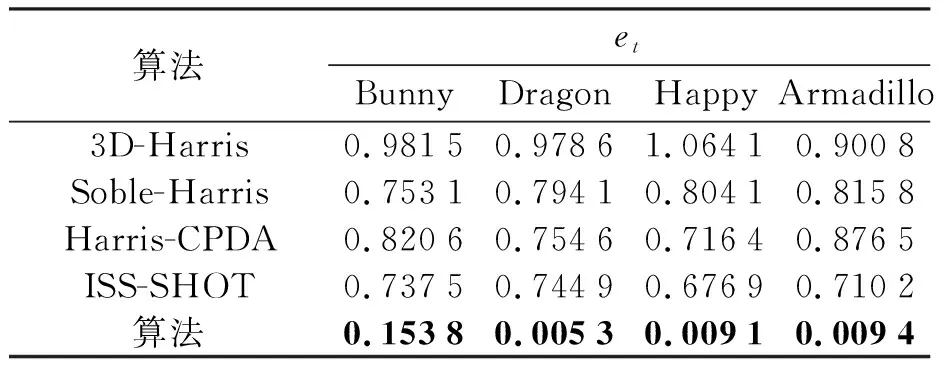
表3 粗配准算法的et对比

表4 配准所需时间T对比

从表2～4可看出，提出的算法配准精度高于其他算法，尤其是在Bunny、Dragon以及Happy这3个模型当中，提出算法的精度远远高于其他4种算法.在配准效率方面，由于加入了特征保留权值，减少了运算时间，所以配准所消耗的时间均低于其他4种算法.在Armadillo模型当中，虽然旋转矩阵误差eR表现不是很突出，但是平移矩阵误差et和配准时间都大大低于其他算法.因此，提出算法可以有效地完成三维点云的粗配准任务，而且在保证配准精度的同时也提高了配准的效率.

3 结 论

针对无初值情况下点云粗配准精度和效率低的问题，提出一种基于特征匹配的三维点云粗配准算法.首先对带配准的点云进行特征提取，然后根据特征信息建立特征直方图，将刚性不变约束和RANSAC相结合得到匹配点对，最后进行刚性变换估计得到旋转矩阵和平移向量.根据局部变化信息提取特征点，提出了一种新的特征直方图建立方法，加入特征保留权值提高了算法的配准效率.通过多组的实验数据表明，提出的方法可以很好地完成点云配准任务，并且具有较高的配准效率，可以为后续的精确配准工作提供良好的初值，但提出的粗配准算法存在鲁棒性不高的情况，因此下一步的工作是在保证配准的有效性和效率的前提下，进一步提高算法的鲁棒性.