改进遗传算法及其在倒立摆控制中应用研究

董如意，刘亚男

(吉林化工学院 信息与控制工程学院，吉林 吉林 132022)

遗传算法[1-2](Genetic Algorithm,GA)是目前应用范围最广的元启发式算法之一，通过模拟生物“优胜劣汰、适者生存”的自然法则，采用并行的概率搜索机制，寻找适应度函数值的最优化结果，对目标函数没有过多限制，具有良好的全局搜索能力[3].但标准遗传算法中交叉算子和变异算子使用的是固定数值，导致寻优过程中种群多样性下降，过早收敛于局部最优解，严重影响了最优解的质量和搜索速度.在众多对遗传算法的研究中，使用数学计算方法来克服传统算法对初始信息极其敏感的缺点，取得了较大的成功[4]，然而大多改进方法目前仅集中在理论研究方面，对于实际工程问题的求解还需要进一步完善.因此，结合数学方法，针对传统遗传算法本身存在的缺点，设计了一种自适应调整交叉和变异的遗传算法，同时将改进的遗传算法应用于倒立摆控制器的设计中，实验表明，相比于传统遗传算法，改进的遗传算法对倒立摆系统关键参数的寻优效果更好，倒立摆达到稳定的次数更多.

1 遗传算法及改进

1.1 标准遗传算法

遗传算法是1975年由Holland提出的一种随机的并行搜索算法，主要模拟生物群体在自然选择中的作用机理和繁衍过程，包括生物增殖、杂交和基因突变等遗传现象.与其他数值优化算法相比，遗传算法具有很好的全局收敛性和普适性，广泛应用于人工智能、工业优化、数学求解以及相关工程实践中.

标准遗传算法是基于非确定性的概率搜索机制，将问题的可行解进行二进制编码，模拟生物的染色体特征，通过计算适应度值的来保留最佳的可行解，然后按照一定的概率完成染色体的交叉和变异，再以精英选择的方式保留最优个体的特征，以此不断迭代，直到找到全局适应度值最优的可行解.标准遗传算法的优化流程图如图1所示.

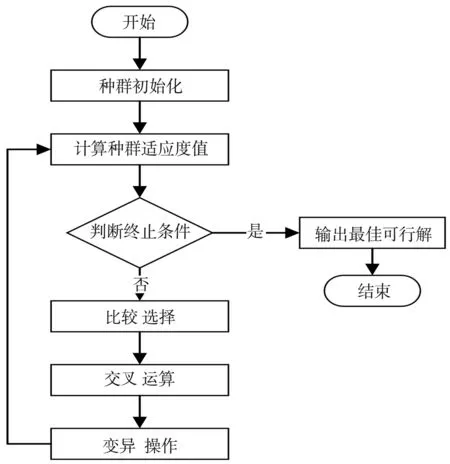
图1 标准遗传算法流程图

尽管遗传算法具有操作简单、实用性强的特点，同时也存在明显的不足，例如局部搜索能力差、容易早熟、后期收敛速度慢、收敛精度低等.特别是标准遗传算法的交叉率和变异率为固定的数值，会导致在算法优化的后期使种群失去多样性的优势，面对较复杂的目标函数时，严重影响算法的性能.因此，针对标准遗传算法的缺点，结合数学理论，提出了一种改进的遗传算法.

1.2 改进遗传算法

中改进的遗传算法主要解决以下几个问题：

1.在最初迭代中，交叉率、变异率均不能降为零，又要提高对最优解的搜索速度.

2.当平均适应度值与最大适应度值的差值较大时，迭代过程不会出现线性变化，有效避免种群进化迟缓或停滞.

3.算法后期，为了保留优良个体，在满足精度的情况下，缓慢减小交叉率和变异率.

基于上述问题，对交叉率、变异率等特征进行了一系列非线性的、可自适应性的优化调整，以此来提升算法的优化能力.首先，利用sigmoid函数对交叉率进行改进，该函数的数学模型为S形曲线，增长趋势会随参数的变化而逐渐平缓，简化方程如式(1)所示.

(1)

sigmoid函数的仿真曲线图2所示.

x图2 sigmoid函数曲线图

通过基于sigmoid函数的自适应调节，遗传算法的交叉率在前期迭代过程中保持最大值，增加个体的多样性，提高寻优过程的全局搜索能力，经过一定次数的迭代后，交叉率会逐渐降低至最小值，从而完成全局搜索向局部搜索的平稳过渡，由改进的式(2)可知，Pc中favg和fmax随sigmoid函数进行非线性调整.

(2)

其中，f是个体适应度；favg是适应度值的平均值；fmax是适应度值的最大值；fmin是适应度值的最小值；f′代表在交叉个体中择优选取；k1是曲线平滑参数；Pc max，Pc min是交叉率的最大值和最小值.

为了进一步提高遗传算法的局部搜索能力，采用一种新的变异方式，即十进制变异法.Pm按照个体适应度值从小到大排序，较优秀的个体排在后边，把选择的优秀个体转成十进制，然后以循环方式加上递增的十进制数，该十进制数由当前变异率的最大值和最小值确定，最后选择一个最优个体进行变异.十进制变异法可以在一定程度上增加变异的随机性，扩展变异的范围和概率，让寻优结果可以更好地跳出局部最优解，保证收敛速度的同时提升算法的精确度.变异过程的调节如式(3)所示.

(3)

其中，T为最大迭代次数；t为当前迭代次数；Pm max，Pm min为变异率的最大值和最小值.

2 基于遗传算法的倒立摆智能控制

2.1 直线一级倒立摆的数学模型

倒立摆系统是一种十分经典的工程欠驱动体系[5]，是控制、数学、力学等理论的有机结合和综合应用.由于倒立摆系统具有高阶非线性、自然不稳定等在复杂工程中也十分普遍的特性[6]，其相关控制算法的研究在机器人、智能控制[7]以及其他诸多领域均有所应用.因此，将倒立摆控制作为研究的控制对象，具有很好的数学理论实践意义和技术工程分析指导研究意义[8-9].

由于直线一级倒立摆自身具有非线性及不稳定性，可以适当忽略个别次要因素，例如角度细小偏差、系统摩擦力等，从而简化该运动系统.倒立摆控制系统的数学模型如图3所示.

图3 直线一级倒立摆的结构示意图

2.2 倒立摆控制模型

图4 倒立摆控制模型

遗传算法优化倒立摆系统的流程如下：

1.随机产生初始种群.

2.按照指定策略判断参数的适应度是否达到优化准则或终止条件，若可行，输出最优解，判断结束；否则，进行下一步.

3.依据适应度值选择父代种群，选择适应度较高的参数，适应度较低的参数被淘汰.

4.按照一定的方法对父代的染色体进行交叉操作，生成子代.

5.对子代染色体进行变异操作.

6.交叉和变异产生新一代种群，随即重复执行步骤2，直到产生最优可行解.

3 仿真结果与分析

3.1 模型参数

使用固高公司开发的倒立摆系统模型，模型具体参数如表1所示.

表1 实际模型参数

3.2 数据分析

在改进遗传算法优化倒立摆系统的问题上，种群大小、迭代次数、交叉、遗传算子对倒立摆系统的优化效果都有着一定的影响，而重点研究基于sigmoid函数的自适应调整的交叉率和基于十进制的变异率对倒立摆稳定性的影响.因此采用控制变量法，设置种群大小为20，迭代次数为200次，在Python3.8上进行仿真实验，比较标准遗传算法和改进遗传算法的优化能力.

表2对比分析了标准遗传算法下恒定的交叉率和变异率与改进遗传算法的自适应调整交叉率和变异率的区别，从表中可以清楚地体现出，改进后的遗传算法对倒立摆的稳定效果更好.

表2 标准遗传算法与改进遗传算法对比

表3为表2的进一步解释说明，是在不同迭代次数下的参数值，随着迭代次数的增加，优化后的参数值效果更好，倒立摆的稳定效果更好.

表3 优化后的参数值

图5为两种算法在不同迭代次数下的倒立摆坚持次数的折线图，从中可清晰看出，标准遗传算法对倒立摆稳定控制参数的优化效果并不理想，结果有大提升空间.改进遗传算法下倒立摆坚持的次数明显提高，随着迭代次数的不断增大，倒立摆的稳定效果更好.

迭代次数图5 倒立摆坚持次数折线图

该实验的仿真结果表明，改进的遗传算法在实际测试上展现了良好的可行性，能够更好、更快地找到优质可行解.经过多轮200次迭代测试下，改进的遗传算法相比标准遗传算法对倒立摆的稳定控制效果更好，即该倒立摆已经实现稳定控制.

4 结 论

通过分析标准遗传算法中交叉算子和变异算子的特点，分别对二者进行了自适应调整，利用sigmoid函数实现了前期全局搜索向后期局部搜索的平稳过渡，弥补了标准遗传算法种群多样性降低和搜索速度迟缓等不足.十进制变异方法在保留了最优个体的同时，增大了个体跳出局部最优的能力，避免了算法早熟，提升了最优解的品质.以直线一级倒立摆智能控制系统作为主要研究对象,基于改进的遗传算法对倒立摆智能控制系统进行参数优化，并通过仿真实验得出，相较于原始遗传算法，改进的遗传算法在倒立摆稳定控制上的优化效果更好.