基于经验模态分解的爆破延期识别优化方法

易文华 ， 刘连生， 闫 雷， 董斌斌， 刘 伟， 杨 砚

(江西理工大学 资源与环境工程学院，江西 赣州 341000)

随着爆破行业的发展，延期爆破作为降低爆破地震效应的一种控制技术越来越多地应用到工程实践，对爆破振动信号进行延期分析是爆破参数设计优化和爆破盲炮识别中常用的分析方法[1-2]；但在爆破工程作业中，由于受复杂地质、地形条件、施工质量等因素的影响，爆破信号中蕴含着丰富的振动状态信息且彼此之间互相干扰，对信号延期识别精度造成了影响。

目前延期爆破延期识别的主要方法有八线示波器和金属拉线法[3]、小波时-能密度[4-5]和经验模态分解(empirical mode decomposition, EMD)识别等方法。但八线示波器和金属拉线法操作复杂，成本较高，且精度较低。随着振动信号分析理论在爆破工程中的发展，凌同华等利用小波变换的时-能密度法分析信号能量突变的优势，有效地识别出延期爆破延期时间，但小波变换分解的精度依赖小波基的选择，选择不同的小波基会产生不同精度的误差。随后张义平等[6]利用EMD法将爆破振动信号分解成若干个本征模函数(intrinsic mode function, IMF)分量,继而通过Hilbert变换提取主IMF分量的包络幅值对实际爆破延期时间进行识别。

由于EMD能自适应地将信号按不同时间尺度进行分解，可以很好地提取非平稳信号变化的特征[7]；与小波时-能密度法相比，EMD识别法不需要选择基函数且自适应性强。但EMD识别法在分解信号过程中，分解出的IMF分量之间会出现模态混叠现象[8-11]。针对这个问题，Wu等[8]提出了集总经验模态分解(ensemble empirical mode decomposition，EEMD)方法来抑制模态混叠现象，得到了较好的效果，但对低频率比例的混合信号抑制效果不佳。司莉等[9]镜像延拓方法以及高频谐波法对EMD分解不完全现象进行了抑制，但选择的频率需要根据异常事件及基础信号的频率反复测试得出，具有较大的不稳定性。詹瀛鱼等[10]提出了基于解相关多频率经验模态分解方法，通过添加掩蔽信号和嵌入相关系数处理， 抑制了模态混叠现象。李晓斌[11]采用了Ort判别法研究出对IMF分量进行完全正交化处理能够有效地消除模态混叠现象。因此分解出的IMF分量之间是否具有混叠现象可由正交性来判断。

针对上述问题的优缺点，本文提出了基于主成分分析(principal component analysis，PCA)的完全正交经验模态分解(principal empirical mode decomposition, PEMD) 方法。由于模态混叠是由于EMD分解出的IMF分量之间的信息相互耦合，本质为 IMF 分量之间不完全正交[12]，故可利用主成分分析[13-14]能将具有相关性的数组转化为正交数组的特性，对IMF分量进行主成分分析，实现各IMF分量之间完全正交化，从而抑制模态混叠现象[15]，最终提升EMD方法对爆破振动信号延期识别的精度；并通过相似物理模拟试验和德兴露天台阶延期爆破试验，与EMD方法进行对比，检验和评价PEMD方法的爆破延期识别效果。

1 基本原理简介

经验模态分解是由Huang等[16]提出的一种信号时频分析方法，该方法能够自适应地将原始信号x(t)分解成一系列IMF分量和一个残余量。其中IMF分量突出了信号的局部特征，残余分量则代表信号中的缓慢变化量。分解过程[17]可表达为

(1)

式中：ci(t)为第i个IMF分量；rn(t)为残差，也称信号的趋势项。

主成分分析，是Hotelling[18]在1993年提出的一种多变量统计方法，通过正交变换将一组不完全正交的原始数据矩阵转X换为完全正交矩阵V，在不损失原信号信息的前提下，达到正交化的目的。即

(2)

式中：Λ为非零对角元素组成的特征值矩阵；V特征向量组成的正交矩阵；n为采样点的个数。

2 完全正交经验模态分解

模态混叠现象的产生与 EMD 不完全正交分解有关，分解出的各IMF分量之间信息相互耦合。因此需要采用一种处理方法使各IMF分量之间满足完全正交性，就能够对模态混叠现象进行有效地抑制。本文提出一种基于PCA对EMD进行辅助分解的算法PEMD，通过对混叠的IMF分量进行主成分分析，实现各IMF分量之间完全正交化，从而提高EMD延期识别精度。该算法的实现流程如图1所示。

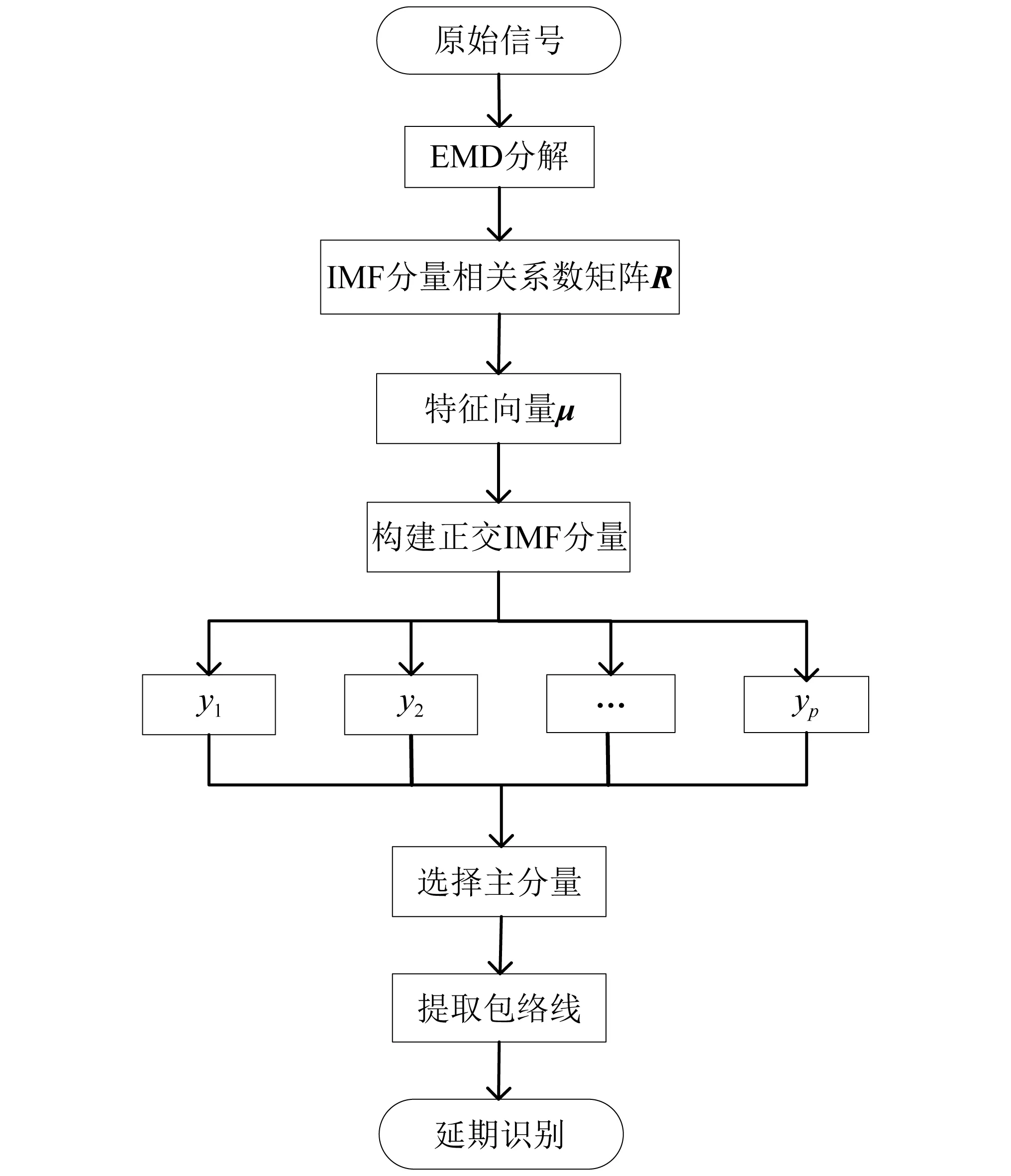
图1 PEMD算法流程图Fig.1 PEMD algorithm flow chart

具体步骤如下:

步骤1将原始信号x(t)通过EMD分解成m个IMF分量，每个分量都取n个采样点。

步骤2假设各个IMF分量分别为x1,x2,…,xm，第i个采样点的第j个分量的取值为aij

步骤3计算IMF分量协方差矩阵R

(3)

R=(rij)m×n

(4)

式中，R为相关系数矩阵。

步骤4计算相关系数矩阵R的特征值λ和特征向量u，由特征向量组成m个正交IMF分量yi,i=1,2,…,m为

(5)

步骤5根据正交IMF分量的幅值和波形衰减特征选择主分量[19-20]。

步骤6对主分量进行Hilbert变换，提取包络线

(6)

z(t)=c(t)=jH[c(t)]=a(t)ejφ(t)

(7)

式中：pv为柯西主值(cauchy principal value)；a(t)为解析信号z(t)的幅值,也称为信号的包络。

步骤7对主分量包络线的峰值点进行识别，得到实际的延期时间。

通过将EMD的自适应性和PCA的完全正交性特点融合起来，对EMD分解出的IMF分量进行完全正交化处理，可以有效地降低各IMF分量之间的相关性，从而达到抑制信号的模态混叠现象，最终提高振动信号EMD爆破延期识别精度。

3 相似物理模拟试验

3.1 相似物理模型

由于露天边坡现场地质地形条件复杂，外界干扰因素对试验研究影响较大，为了尽量控制其他外界的干扰因素，可根据爆破相似理论[21]，在满足与露天边坡现场的几何、材料、动力以及边界条件相似的情况下得到相似的结果，对新方法的初步研究具有重要意义。因此，为了构建露天边坡相似物理模型，结合露天边坡几何形状将模型设计成四周高边坡台阶、中间凹陷的形态，选用的几何缩比为1 ∶100，同时为尽量满足露天边坡岩体材料特征要求，选用了等级为P·O 42.5的硅酸盐水泥、细沙及水三种材料，选用的配比(水 ∶水泥 ∶砂子)为0.44 ∶1 ∶1.5，最后为使模型的动力以及边界条件与露天边坡相似，设计过程中尽可能加大了模型的尺寸长度以改善边界效应，设计模型的尺寸为270 cm×270 cm×110 cm，其剖面图如图2所示。

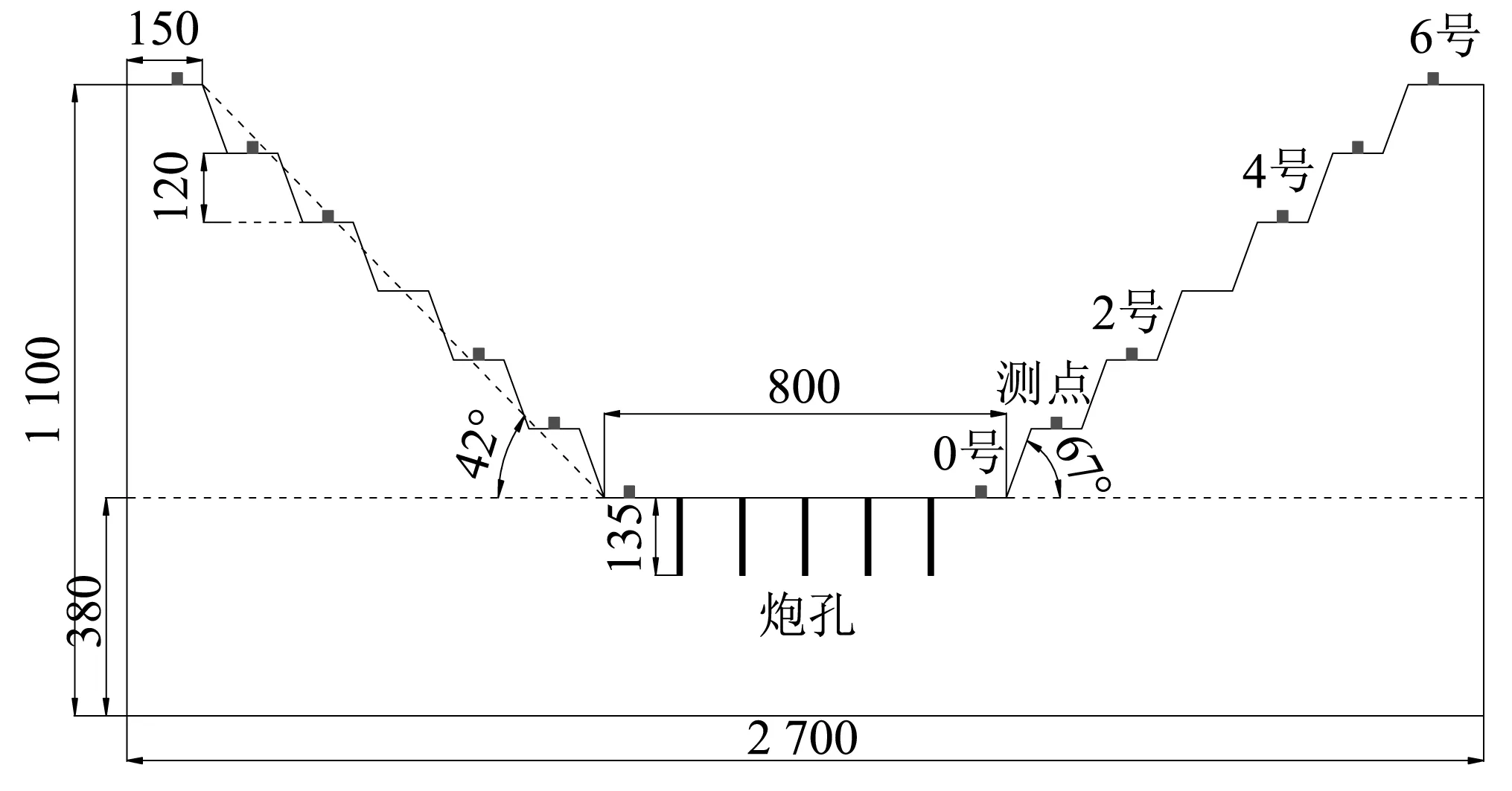
图2 相似物理模型(mm)Fig.2 Similar physical model(mm)

其中，设计模型底座高38 cm，在底座之上共设计4个台阶面，各台阶面之间高程差均为24 cm，台阶总高72 cm，模型总高度110 cm，台阶坡面角均为67°，最终边坡角42°。模型底座中心区域设计为炮孔布置区，以12.5 cm的孔间距及排间距共布置25个炮孔，炮孔深度13.5 cm。平台包括最底层一共4个，由最底层到最上层台阶分别编号为0号、2号、4号和6号，以0号平台为基准，各台阶爆心距和高程差见表1。

表1 爆心距与高程差Tab.1 The difference between the burst distance and elevation cm

3.2 爆破延期识别

3.2.1 EMD识别

下面基于相似物理模型，利用本文提出的PEMD方法与EMD方法对一组典型的爆破振动信号进行延期识别对比。本次试验采用隆芯一号系列数码电子雷管四孔12 ms延期爆破起爆，在6号台阶处布置振动监测点，试验期间所有爆破均设置为单孔单发电雷管起爆。选择一组典型爆破振动信号进行分析，其速度时程曲线如图3所示。

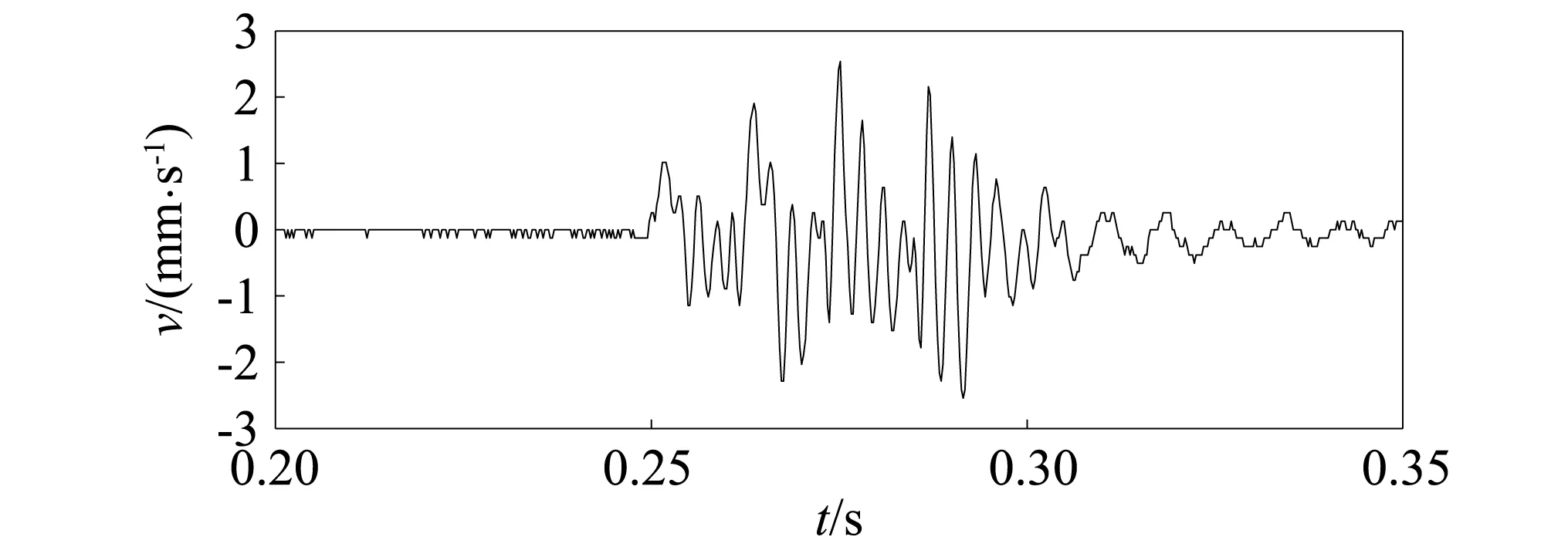
图3 速度时程曲线Fig.3 Velocity time-history curve

对其进行EMD分解，获取了13个频率从高到低依次排列的IMF分量，(篇幅有限，仅列前6个IMF分量)，对其进行EMD分解，获取了13个频率从高到低依次排列的IMF分量，并通过Hilbert变换做出各分量的包络线，如图4所示。

图4 IMF分量及包络线Fig.4 IMF components and envelope

由图4可以看出，IMF1幅值较大，波形衰减明显，携带了爆破的大部分信息，且包络线波峰最接近四孔爆破效果，因此考虑选IMF1分量作为主分量，对其包络线进行进一步分析，如图5所示。

由图5可知，EMD识别法识别出了6个峰值点，分别是(0.216，0.277),(0.256，0.844),(0.267, 1.257),(0.278, 1.837),(0.290, 2.260)和(0.302,0.361)。延期时间分别为40 ms,11 ms,11 ms,12 ms和12 ms。由于本次爆破试验设计为12 ms延期的四孔爆破，在此EMD识别法识别出了6个峰值点，很明显EMD分解出的主IMF分量受到了外界因素的干扰，出现模态混叠现象，影响了EMD识别法的精度。

图5 主分量包络线Fig.5 The envelope of the principal component

3.2.2 改进算法PEMD识别

由于EMD不完全正交分解，导致分解出的各IMF分量出现模态混叠现象，造成延期识别精度的降低，而PCA能够将不完全正交的多个向量转变成完全正交向量，故在此引入PCA方法对EMD进行改进。

将原始信号进行EMD分解，得到13个IMF分量xj，j=1,2,…,13，计算各分量的相关系数矩阵R如表2所示。

表2 各IMF分量相关系数Tab.2 The correlation coefficients of IMF components

继而计算相关系数矩阵的特征向量μ

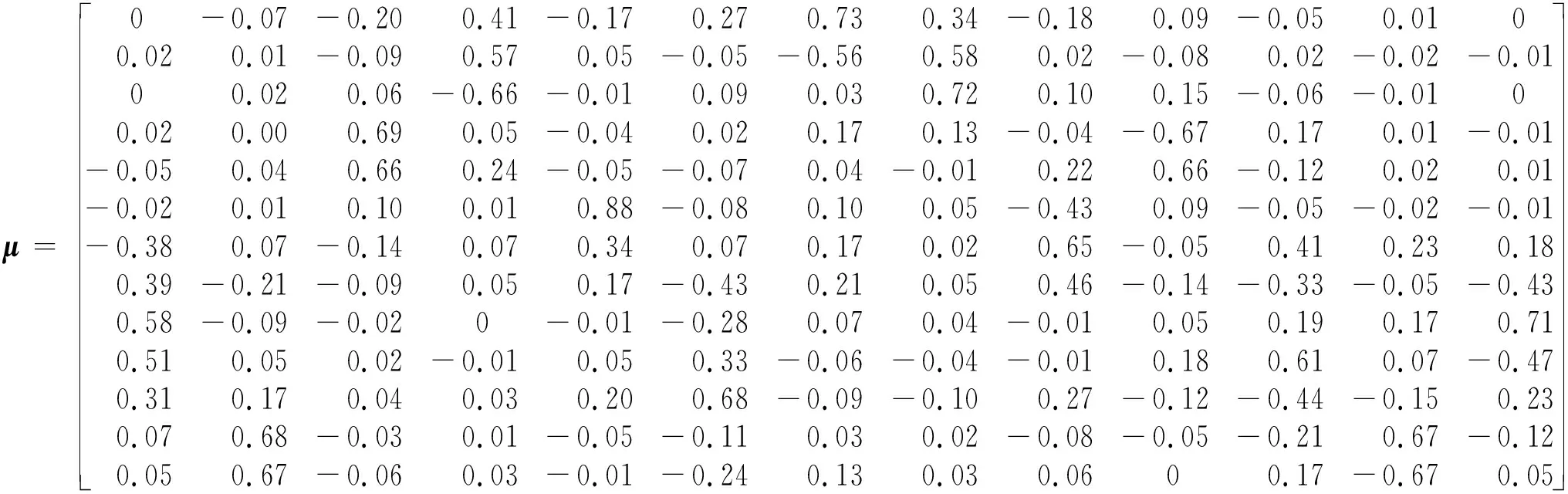
则由特征向量构建正交IMF分量yj

对各正交IMF分量进行Hilbert变换，提取包络线如图6所示。

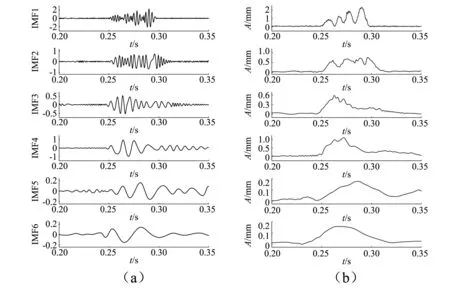
图6 正交IMF分量及包络线Fig.6 Orthogonal IMF component and envelope

由图6可以看出，IMF1 幅值较大，波形衰减明显，故选择为主分量，将其与EMD主分量包络线进行对比，如图7所示。

图7 主分量包络线对比Fig.7 Comparison of principal component envelope

由图7可知，经过PEMD处理后的幅值包络图识别出了四个峰值点，分别是(0.256，0.844)，(0.267, 1.257)，(0.278, 1.837)，(0.290, 2.260)，延期时间分别为12 ms，12 ms，12 ms，误差为0。与EMD识别结果相比，有效地去除了模态混叠现象，提高了识别精度。

3.3 PEMD算法稳定性检验

试验控制高程和延期时间两种变量进行稳定性检验，选择同一高程(4号台阶)不同延期时间(10 ms,16 ms,21 ms)起爆和不同台阶(2号，4号，6号台阶)同一延期时间(16 ms)起爆，雷管个数均设为3发，理论上爆破振动信号将由3段爆破振动波叠加而成。其爆破振动速度时程曲线如图8所示。

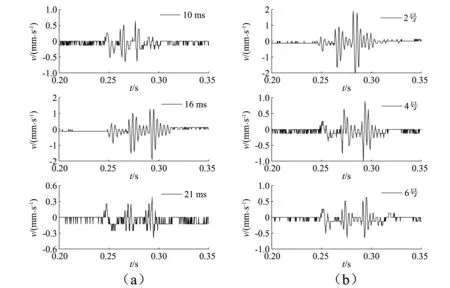
图8 速度时程曲线Fig.8 Velocity time-history curve

首先对同一高程不同延期时间爆破振动信号进行EMD，PEMD识别，如图9所示。

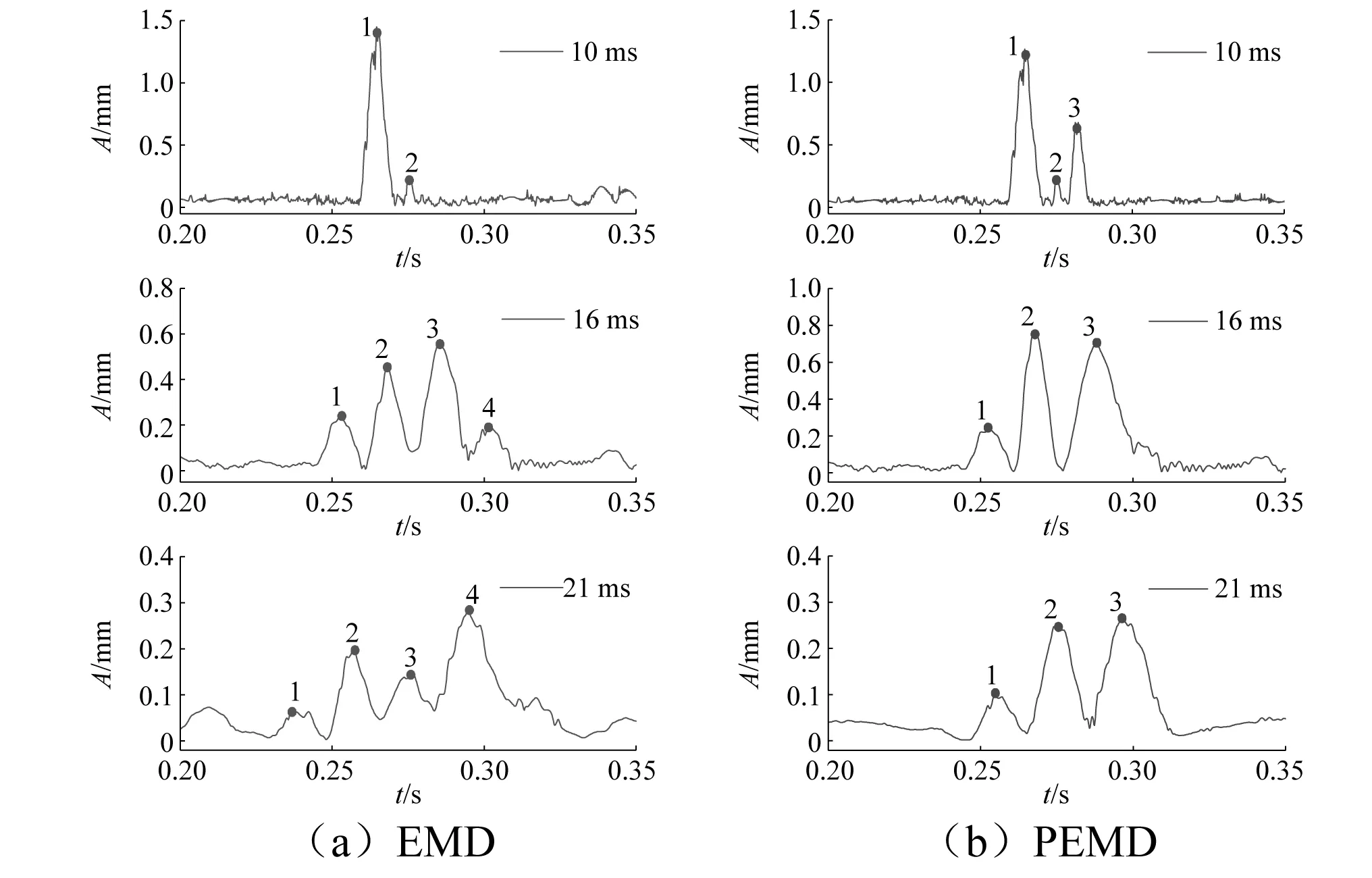
图9 不同延期时间包络线对比Fig.9 Comparison of envelops with different delay time

由图9可知，EMD识别法对10 ms，16 ms，21 ms延期信号分别识别出2个、4个、4个峰值点，表明EMD对3段爆破振动波的识别发生误差；而PEMD在2号、4号、6号台阶处均识别出3个峰值点，精确识别出了3段爆破振动信号。

继而对同一延期时间不同高程爆破振动信号进行EMD和PEMD识别，如图10所示。

由图10可知，EMD识别法在2号、4号、6号台阶处分别识别出2个、4个、2个峰值点，而PEMD在2号、4号、6号台阶处均识别出3个峰值点，因此PEMD与EMD相比，识别精度不受延期时间和高程因素的影响。为了进一步量化对比两者的识别误差，计算出各峰值点的延期时间如表3所示。

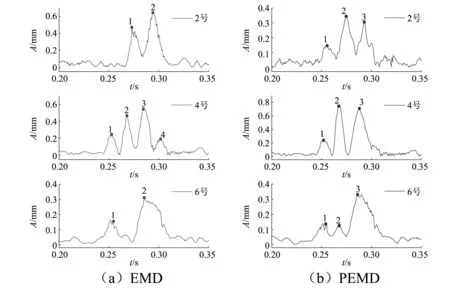
图10 不同高程包络线对比Fig.10 Comparison of envelope at different elevations

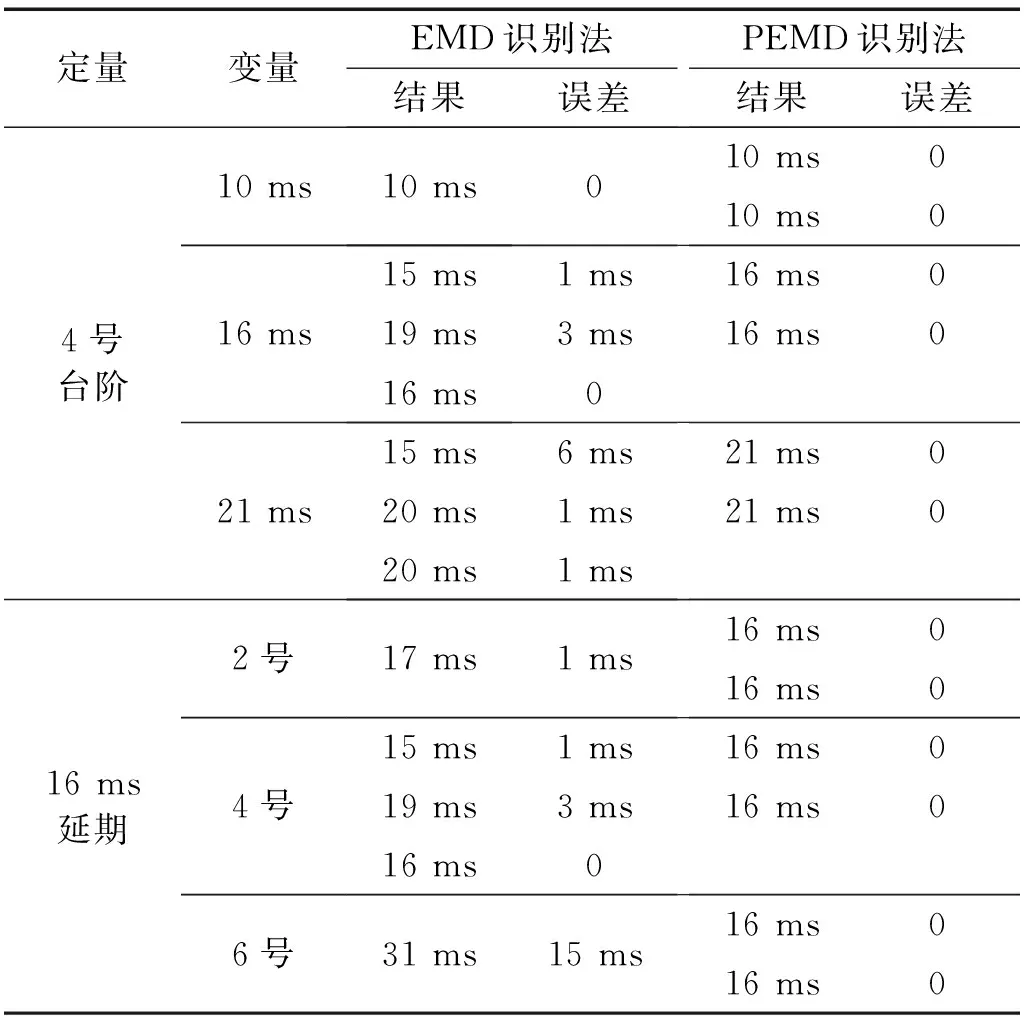
表3 峰值点延期时间Tab.3 The delay time of the peak point

由表3可知，从不同延期时间分析，EMD识别法在4号台阶处10 ms，16 ms，21 ms的平均误差为4 ms，PEMD为0；从不同高程分析，在16 ms延期时间的2号、4号和6号台阶处，EMD平均误差为6 ms，PEMD为0。故无论是从延期时间还是高程进行分析，PEMD识别精度均优于EMD。

4 露天边坡延期爆破试验

4.1 试验背景

德兴铜矿位于江西省德兴市泗洲镇，黄牛前露天采矿边坡位于铜厂采区的东部，边坡设计总体坡角为46°，边坡走向144°～152°，倾向234°～242°，倾角41°～42°。本文采用德兴黄牛前露天采矿边坡开挖爆破数据，爆破振动测试所采用的是Blastmate III型号爆破振动监测仪，采样频率为4 096 Hz。爆破区域位于铜厂采区215 m边坡台阶，爆破测振过程中在黄牛前西侧边坡170 m，230 m，260 m，290 m水平上分别布置了2号、4号、6号、8号测点，如图11所示。

图11 测点布置图(m)Fig.11 Layout of measuring points(m)

以爆区坐标为基准，各水平测点的爆心距和高程差，如表4所示。

表4 测点高程差与爆心距Tab.4 The difference between the burst distance and elevation cm

4.2 爆破延期识别

本次爆破为逐孔起爆，延期时间在42～694 ms，炮孔数为38个，其相应的爆破网路及延期设计时间,如图12所示。

图12 爆破网路及延期时间(ms)Fig.12 Blasting network diagram and delay time(ms)

取2号、4号、6号、8号水平测点爆破振动信号进行EMD、PEMD识别，并与爆破延期设计值进行对比，结果如图13所示。

由图13可知，PEMD与EMD相比，对各水平测点爆破振动信号延期的识别结果与设计值更为接近，为了进一步量化对比两者的精度，定义延期时间的识别率为

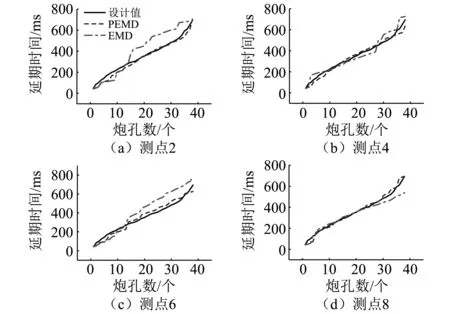
图13 识别精度图Fig.13 Identification precision diagram

(8)

式中:δ为识别值与理论值的相对误差；n为炮孔个数。

计算得到各测点的延期时间识别率，如表5所示。

表5 测点延期时间识别率Tab.5 Recognition rate of delay time of measuring point %

从表5可知，PEMD在各测点处的识别率均高于EMD，且EMD识别率在74%～91%内波动，是因为EMD识别信号时会产生模态混叠现象，随着混叠现象程度的不同，识别率也随着发生波动；而PEMD由于解决了EMD模态混叠的问题，识别率大幅提升，且稳定保持在90%以上。由于PEMD对炮孔的延期识别率大幅提升，将各炮孔的延期识别值与设计值进行对比，可识别爆破过程中是否出现盲炮，同时结合炮孔布置图，能够进一步确定盲炮的具体位置，对解决爆破工程中的盲炮识别问题具有重要意义。

5 结 论

为了提高EMD爆破延期识别精度，本文提出了一种基于PCA的PEMD方法，利用PCA能将具有相关性的数组转化为正交数组的特性，抑制了振动信号EMD分解过程中的模态混叠现象，提高了爆破延期识别的精度。

通过相似物理模型试验分析结果可知，PEMD 能够有效地抑制振动信号EMD分解时出现模态混叠现象，爆破振动波峰值点的识别精度显著提高，并通过控制高程和延期时间变量对PEMD方法的稳定性进行了检验；同时以露天边坡延期爆破试验为例，结果表明PEMD能够对各水平测点爆破振动信号实现90%以上的识别率，对后续爆破工程中爆破参数设计优化和盲炮识别具有重要的意义。