非对称制动压力对汽车低频制动尖叫的影响
2022-02-16吴奕东陈晶艳余家皓
吴奕东, 陈晶艳, 余家皓
(广州汽车集团股份有限公司汽车工程研究院,广州 511434)
近年来,汽车的制动噪声问题日益引起消费者的关注。汽车的制动噪声可以大致分为颤振鸣音、低频尖叫和高频尖叫三类,对应频率分别为50~1 000 Hz,1 000~6 000 Hz和6 000 Hz以上。制动摩擦尖叫是困扰学术界和工业界的世界性难题,目前对其产生机理尚未有统一的认识[1]。
目前,汽车制动尖叫的发生可以认为与摩擦片-制动盘的接触特性有着重要的关联,一些研究以摩擦片和制动盘的接触面为研究对象,提出了摩擦特性理论及摩擦自锁理论来解释产生汽车制动噪音的原因[2-6]。摩擦副的力学行为对制动噪声有非常显著的影响,但除了制动盘与摩擦片外,制动器其他子结构的摩擦接触或共振可能会导致制动尖叫的产生[7-8]。模态耦合自激振动理论从制动器结构角度解释制动尖叫产生,认为制动尖叫是系统摩擦耦合过程中各部件结构参数匹配不当所导致的[9-11]。建立在模态耦合理论基础上的复模态分析法被广泛应用在降低汽车制动噪音的方法中。摩擦力的存在使系统的刚度矩阵不是对称的,从而会产生复特征值,进一步地可以根据复特征值的实部对系统的稳定性进行判断。随着计算机技术的发展,制动器的复模态有限元数值模拟被广泛应用在汽车制动噪音的研究当中[12-15]。此外,一些研究引入随机和区间不确定性参数对制动器的鸣音进行研究,甄别了不确定性参数对系统稳定性的影响[16-17]。
管迪华等[18-20]提出的能量馈入分析法可以进一步研究制动盘和摩擦片的接触行为制动噪声的影响,改变摩擦片的倒角、摩擦因数或材料参数等对抑制制动噪声均起到有效的作用。后续的一些关于制动器能量馈入的研究都是只关注制动盘和摩擦片所构成的耦合子系统而忽略其他耦合子系统的影响[21-22]。张立军等[23]认为能量馈入会影响制动摩擦尖叫声压幅值变化,制动尖叫的研究要全面考虑整个制动器系统摩擦副的能量馈入情况。汽车制动器在制动过程中由油压提供制动力,在制动盘上产生摩擦力以起到制动的作用。因此,制动器系统中存在明显滑动的摩擦副主要有两个:一个是以制动盘和摩擦片为系统的摩擦副;另一个则是以卡钳和活塞为系统的摩擦副。大多数汽车制动噪声的研究都把关注点放在了前者,而后者在制动尖叫中的影响机理很少有研究。
实际上,随着制动油压的变化,制动尖叫声的大小和频率也有可能随之变化。制动油压不仅直接影响盘片间摩擦力的大小,还影响卡钳与活塞的振动形态。此外,制动力并不是直接作用在摩擦片上的。制动油压直接施加在活塞和卡钳上,通过活塞和卡钳的运动使内外摩擦片收紧,这期间需要通过背板来给摩擦片传递压力。这就有可能导致内外摩擦片所收到的制动压力不相等,在制动盘的两侧产生非对称的制动压力,从而影响制动系统的振动模态。因此,本文基于活塞-卡钳和制动盘-摩擦片这两个摩擦耦合系统的能量馈入情况,探究非对称制动压力下汽车低频制动尖叫的机理。
针对低频制动尖叫现象,本文建立汽车盘式制动器有限元模型,并开展其非对称性和对称性制动压力下的复模态数值仿真。根据复模态特征根的实部找出1 000~6 000 Hz内可能出现低频制动尖叫现象的频率以复现实际的噪声情况。基于能量馈入分析法,建立活塞-卡钳耦合子系统和制动盘-摩擦片耦合子系统,推导出双耦合子系统下制动器的相对能量馈入计算方法。通过馈入能量进一步分析非对称制动压力对制动尖叫的影响机理,为研究汽车制动噪声提供理论依据。
1 能量馈入分析法
1.1 复模态特征分析法
对制动器系统中的各子部件进行有限元离散化,建立制动器的动力学方程为
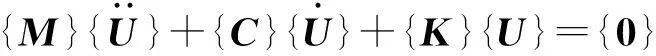
(1)
式中:{U}为各离散点的位移;{M},{C}和{K}分别为离散化的质量矩阵、阻尼矩阵和刚度矩阵。由于摩擦力的存在,刚度矩阵{K}为非对称矩阵,从而导致式(1)的解具有复特征根。
假设{U}={ψ}eλt,代入式(1),可得
(λ2{M}+λ{C}+{K}){ψ}={0}
(2)
式中,{ψ}为特征向量。特征值λ可以写成λ=a+iw的形式,其中:a为特征值的实部,表示阻尼系数;ω为特征值的虚部,表示模态频率。正的实部会使振动扩大,发展为强烈的自激振动,因此通过实部可以确定出系统的不稳定特征频率。
1.2 能量馈入分析法
对于制动器系统,外界的能量输入转化为制动力和驱动力,活塞-卡钳及制动盘-摩擦片这两个子系统有明显的相对运动,从而导致制动器系统发生能量馈入。为了全面地研究制动器的振动情况,建立双耦合子系统的能量馈入模型,即活塞-卡钳耦合子系统模型和制动盘-摩擦片耦合子系统模型。
本文所讨论的相对馈入能量本质上是一种对系统的扰动能量。该能量的产生主要是因为在结构的接触面之间发生了非预期的振动。该非预期的振动方向认为是垂直于相对运动方向的。活塞-卡钳子系统的相对运动方向是制动油压方向,制动盘-摩擦片子系统的相对运动方向是旋转的切向方向。因此本文分别考虑垂直于上述两个方向的相对能量馈入情况。
以活塞-卡钳子系统为例子推导其相对能量馈入的计算方法。活塞和卡钳的内部示意图,如图1所示。图1中的坐标系为全局坐标系。在制动油压的作用下,活塞和卡钳沿着y轴运动。A和B分别为活塞和卡钳的第i组对应节点,对应节点在运动开始前完全重合。卡钳和活塞的接触刚度为k1。

图1 卡钳-活塞耦合子系统示意图Fig.1 Schematic diagram of caliper-piston coupling subsystem
点A和点B的位移分别为Ui,p和Ui,c,其中:下标p为活塞;下标c为卡钳。位移Ui由三个方向的振型系数xi,yi和zi所组成。若各个方向的运动形式为简谐运动,则有
(3)
点A和点B在z方向上的相对位移和受力分别为
zi,p-zi,c=Ai(z),psin(ωt+θi(z),p)-
Ai(z),csin(ωt+θi(z),c)
(4)
Fi(z)=k1(zi,p-zi,c)
(5)
在一个振动周期T内,点A和点B在z方向上馈入的能量为
(6)
将式(4)和式(5)代入式(6)中,可得到
Ei(z),p-c=k1Ai(z),pAi(z),csin(θi(z),p-θi(z),c)
(7)
同理可得到点A和点B在x方向上馈入的能量为
Ei(x),p-c=k1Ai(x),pAi(x),csin(θi(x),p-θi(x),c)
(8)
将所有相对节点在x方向上和z方向上的馈入能量进行求和,则可得到活塞-卡钳耦合子系统的相对馈入能量Ep-c的表达式为
(9)
对于接触刚度为k2的制动盘-摩擦片耦合子系统,在全局坐标系xyz中主要考虑x方向和y方向上的能量馈入,因此制动盘-摩擦片耦合子系统的相对馈入能量Ed-f表达式为
(10)
从双耦合子系统模型的相对能量馈入表达式可知,离散化节点的振幅和相位均会影响系统的相对馈入能量。节点的振幅和相位可通过有制动器的复模态有限元数值模拟计算得到,因此可以把复模态的模拟结果与能量馈入的计算结果相结合对制动尖叫进行分析。
2 制动器系统复模态有限元模拟
2.1 制动器系统有限元模型的建立
基于低频制动尖叫现象,本文开展制动器复模态的有限元数值模拟。制动器系统的有限元模型,如图2所示。图2由制动盘、摩擦片、活塞、卡钳和卡钳支架等主要子结构组成。为了提高计算效率,在保证计算结果准确的前提下,制动器有限元模型使用C3D4单元划分,单元尺寸为2.5 mm(制动盘直径约320 mm),全局单元数量5×106个,为了计算系统的相对馈入能量,活塞与卡钳之间、摩擦片与制动盘之间接触位置的网格完全重合。除了摩擦片外,制动盘、卡钳、卡钳支架和活塞等部件均视为各向同性材料,各主要部件的材料参数,如表1所示。
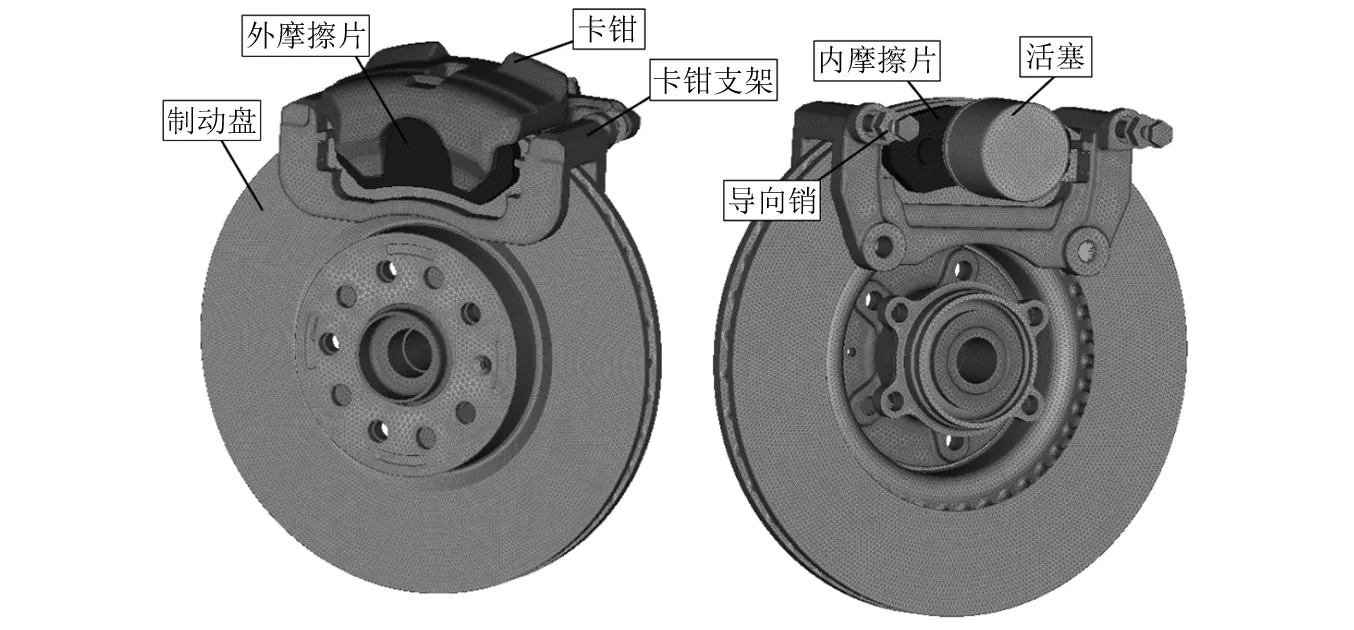
图2 盘式制动器系统有限元模型Fig.2 Finite element model of disc brake system

表1 主要部件的材料参数Tab.1 Material parameters of the components
摩擦片为各向异性材料,在摩擦片的局部坐标系中,x-y平面与制动盘面平行,x方向为摩擦片的运动方向,z方向为摩擦片平面的法向。摩擦片的材料参数,如表2所示。在有限元的复模态分析中采用部分非线性摄动模态分析,首先进行非线性静力分析。为了使计算结果收敛,在运动开始前让摩擦片和制动盘先产生接触,随后释放预接触的同时施加油压和制动盘的转动速度。

表2 摩擦片的参数Tab.2 Material parameters of the friction pads
设置制动油压的取值范围在0.2~1.4 MPa,每隔0.2 MPa施加取一种油压工况,制动盘的转动速度为1 rad/s。在加载过程中保持油压和制动盘转速恒定,从而对制动盘添加转动效应。复模态分析设置在非线性静力分析之后,求解范围在7 000 Hz以内。
2.2 对称性制动压力载荷的设置
提取制动油压0.2 MPa工况下内外摩擦片的接触力,如图3所示。从图3可以看到,在加载过程中内外摩擦片的大小并不是完全重合的,从而在制动盘两侧产生非对称的制动压力。这是因为制动油压的直接作用部件分别是活塞和卡钳,而活塞和卡钳的受压面积由于误差的存在并不是完全相同的,再加上需要通过背板传递制动力,这就有可能导致内外侧摩擦片的大小不一样。

图3 内外摩擦片上的制动力不完全重合Fig.3 The braking forces on the inner and outer friction pads do not coincide completely
为了消除上述制动压力的不对称性,设置对称性的制动压力工况与原工况进行对比,如图4所示。制动压力从原来的施加在活塞-卡钳变成直接施加在摩擦片的左右两侧,从而保证制动盘两侧的制动压力相等。其他边界条件的设置与原来非对称油压工况的保持一致。

图4 对称性压力的施加工况示意图Fig.4 Schematic diagram of symmetrical pressure application condition
3 制动压力的对称性对低频制动尖叫的影响
3.1 制动器的复模态分析结果
不同制动油压下制动器有限元复模态分析结果,如图5所示。在非对称性制动压力下,在上述制动油压范围内共出现三种复特征频率,分别为1 600 Hz附近、3 000 Hz附近和4 000 Hz附近,如图5(a)所示;而对称性制动压力下在低频制动尖叫频率范围内(1 000~6 000 Hz)也会出现四种复特征频率,分别为2 200 Hz附近、2 500 Hz附近、3 200 Hz附近和5 300 Hz附近,如图5(b)所示。从复模态结果来看,改变制动压力的对称性会导致制动器出现完全不一样的复特征频率,但在同一种油压施加方式(对称性或非对称性)上,不同大小的制动油压不会明显改变已有的复特征频率,而会对复特征实部产生显著影响。

图5 各制动油压的复模态分析结果Fig.5 Complex modal analysis results of each brake oil pressure
提取对称性制动压力和非对称性制动压力的振型情况,分别如图6和图7所示。由图6和图7可以看到,在不同复特征频率下,制动器最大振型出现在不同的子部件上。根据所建立的活塞-卡钳耦合子系统和制动盘-摩擦片耦合子系统,可以把最大振型的出现位置归结为上述两个耦合子系统下。在图6中的非对称性制动压力下,1 600 Hz和3 000 Hz附近的最大振型主要以制动盘的振动为主,可以认为是制动盘-摩擦片耦合子系统的振动,而3 000 Hz附近的最大振型出现在导向销处,导向销是随着卡钳的运动而振动的,故可认为是活塞-卡钳耦合子系统的振动;类似地,在图7中的对称性制动压力下,2 200 Hz,2 500 Hz和5 300 Hz附近的最大振型主要以制动盘-摩擦片耦合子系统的振动为主,而3 200 Hz附近的最大振型则是出现在背板处,且制动盘的振动相对不明显,故认为此时是活塞-卡钳耦合子系统的振动占主导。
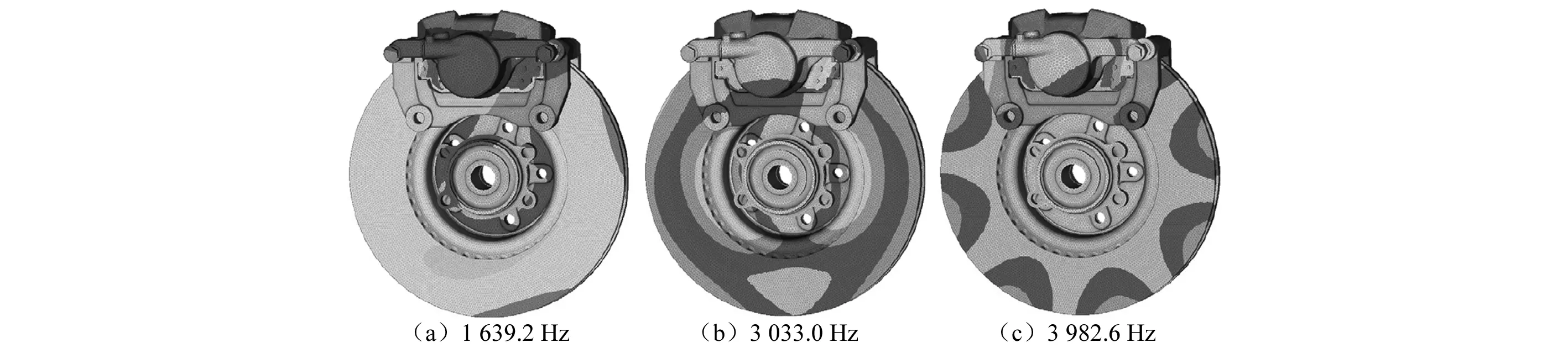
图6 非对称性制动压力下三种复特征频率对应的制动器振型Fig.6 Model shapes corresponding to three complex characteristic frequencies under asymmetric brake pressure

图7 对称性制动压力下四种复特征频率对应的制动器振型Fig.7 Model shapes corresponding to four complex characteristic frequencies under symmetrical brake pressure
3.2 制动器的相对馈入能量情况
活塞-卡钳耦合子系统模型中含有节点588对,制动盘-摩擦片耦合子系统模型中含有节点4 260对。用于计算馈入能量的双耦合子系统模型的节点数量足够多,以保证计算结果的准确性。Bakar等[24]给出了不同界面耦合刚度取值的数量级范围,认为各方向运动均受到严格限制的两子结构界面,耦合刚度值更高,而存在间歇性接触的两子结构间,其耦合刚度则较低。基于材料的局部接触刚度,本研究设定活塞-卡钳耦合子系统中的耦合刚度为1×1010N/m量级,制动盘-摩擦片耦合子系统中的耦合刚度为1×108N/m量级[25]。由于相对馈入能量的表达式(7)中的Ai(z),p和Ai(z),c均已被归一化,故相对馈入能量E的单位与刚度单位相同,为N/m。
不同的非对称性制动压力下,双耦合子系统在1 600 Hz附近、3 000 Hz附近和4 000 Hz附近的相对馈入能量别,如表3所示。为了便于观察,在相同频率下把两个耦合子系统中较大的相对馈入能量在表3中加粗显示。
从表3中可知,在1 600 Hz和3 000 Hz附近,活塞-卡钳耦合子系统的馈入能量总是比制动盘-摩擦片耦合子系统的小,说明此时外界能量输入对制动盘和摩擦片接触界面的扰动更加明显,制动器的运动以制动盘-摩擦片及其邻近子部件的振动为主。此外,从1 600 Hz中的实部数据可以发现,当系统馈入能量的值接近0时,对应频率的复模态就无法被激发。因此,系统馈入能量大于0是低频制动尖叫发生的前提。
在复特征频率4 000 Hz附近,活塞-卡钳耦合子系统的馈入能量大于制动盘-摩擦片耦合子系统的馈入能量,说明此时外界能量输入对卡钳和活塞接触界面的扰动更加明显,制动器的运动主要以活塞-卡钳及其邻近子部件的振动为主。
为了进一步探究相对馈入能量与子部件振型的关系,提取对称性制动压力在5 300 Hz附近馈入能量并列举在表4中。对比可以发现,活塞-卡钳子系统的相对馈入能量远小于制动盘-摩擦片子系统的相对馈入能量,结合图7中的振型情况可知,在该频率下制动器主要以制动盘和背板的振动为主。综合表3、表4和图6、图7可知,耦合子系统的馈入能量越大,复模态最大的振型就会出现在该子系统或其邻近子部件处。
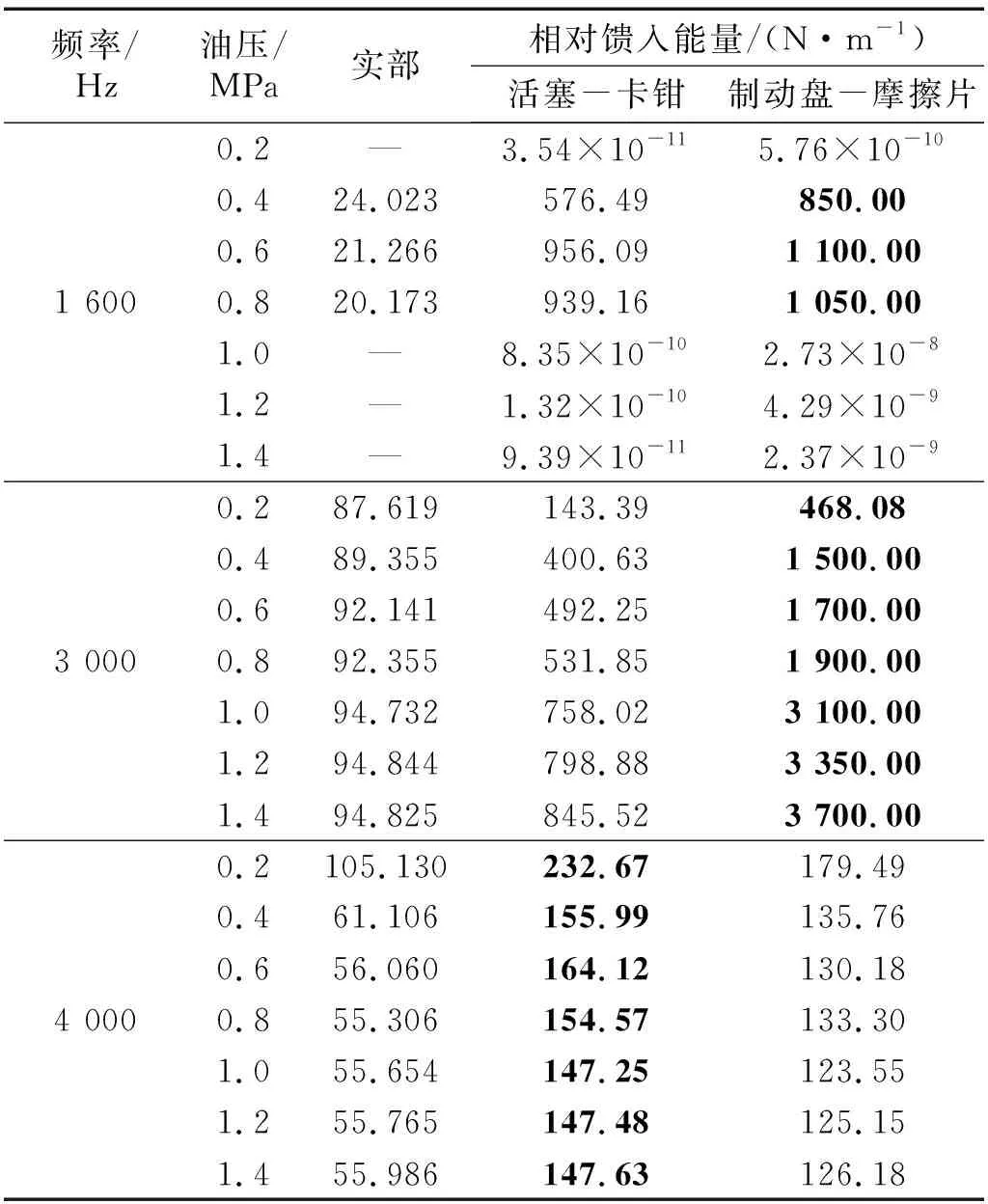
表3 非对称性制动压力下双耦合系统的相对馈入能量Tab.3 Relative feed-in energy of dual coupling system under asymmetric braking pressure

表4 对称性制动压力下5 300 Hz下双耦合系统的相对馈入能量Tab.4 Relative feed-in energy of dual coupling system at 5 300 Hz under symmetrical braking pressure
3.3 制动压力的对称性对低频制动尖叫的影响机理
特征值的实部反映的是阻尼系数。当实部大于0时,系统是一个发散的不稳定系统,a的值越大,说明系统不稳定的概率越大,从而在该频率下更容易发生尖叫噪声。因此,特征值的实部是判断制动器系统是否会发生制动噪音的重要指标之一。结合图5和表3表4可发现,非对称制动压力下,实部最大值出现在3 000 Hz,说明制动器此时的不稳定性更大;而在对称性制动压力下,实部的最大值出现在5 300 Hz,远超过其他复特征频率下的实部,制动尖叫更有可能出现在该频率处。

(11)


图8 归一化馈入能量随制动油压变化的情况Fig.8 Variation of normalized feed-in energy with brake oil pressure
为了进一步探究压力的非对称性程度对低频制动尖叫的影响,在内外摩擦片上设置非对称性压力工况。保持内摩擦片压力不变,设置外摩擦片的压力分别为内摩擦片的90%,95%,105%和110%。若定义对称制动压力的非对称性程度为0,则上述工况的非对称性程度分别为-10%,-5%,5%和10%。内摩擦片在0.8 MPa压力时5 300 Hz特征频率下归一化馈入能量随制动压力非对称性程度的变化情况,如图9所示。曲线呈现中间高两端低的趋势,压力的非对称性程度越高,归一化馈入能量越小,说明两个子系统的馈入能量随着不对称性程度的增强而趋于相近,这不利于明确低频制动尖叫的发生部位。

图9 归一化馈入能量随压力非对称性度变化情况Fig.9 Variation of normalized feed-in energy with the degree of asymmetry pressure
制动盘自由模态的前五阶面外振型如表5所示。对比图7中5 300 Hz制动盘的振型,发现此时活塞-卡钳子系统处的振型很小,制动盘处于第五阶面外振型。说明对称性油压能够很好降低活塞-卡钳的馈入能量,使制动器以制动盘更高阶的面外振动为主,从而提高复特征频率。
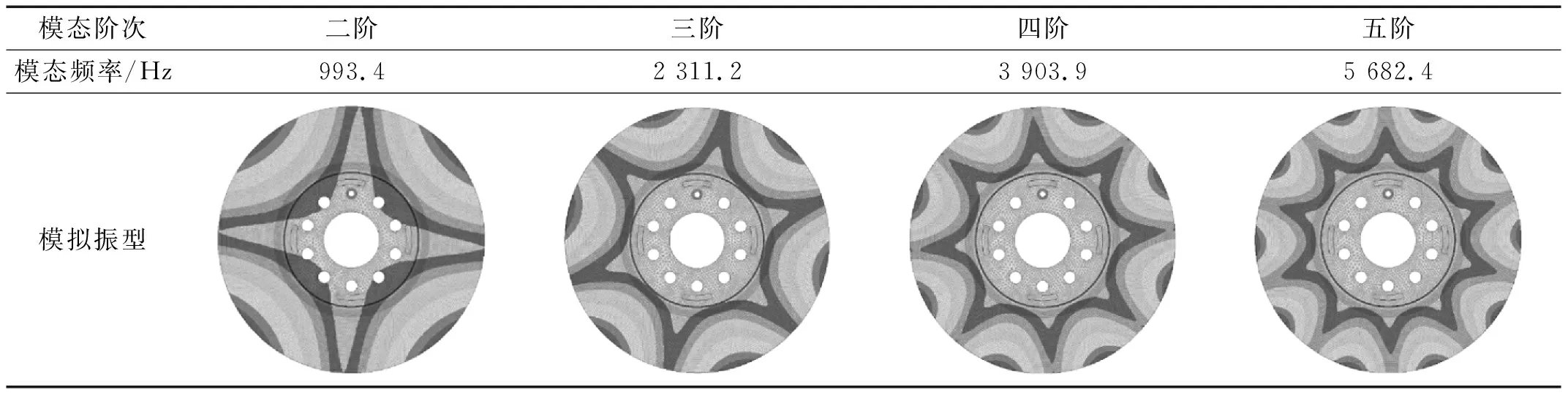
表5 制动盘自由模态的前五阶面外振型Tab.5 The first five out-plane modal shapes of the free mode of the brake disc
由此可见,提高制动压力的对称性可以增大复模态的频率,外界需要更大的能量才能激发对应的制动尖叫。因此,可以通过降低传力部件的摩擦损耗和增加活塞与卡钳受压面积的一致程度来提高制动压力的对称性,从而使低频制动尖叫更加难以被激发。
4 结 论
本研究建立汽车盘式制动器有限元模型,并开展其在对称和非对称制动压力下的复模态数值仿真。通过馈入能量进一步分析非对称制动压力对制动尖叫的影响机理。主要结论如下:
(1)制动器的馈入能量与双耦合子系统中各节点的幅值和相位均有关系。当整体系统相对馈入能量的值接近0时,对应频率的复模态就无法被激发。
(2)耦合子系统的相对馈入能量越大,制动器在该复频率下最大的振型就会出现在该子系统处。在复特征实部最大的频率下,对称性制动压力下的相对馈入能量总是大于非对称性制动压力的,此时制动盘-摩擦片系统的振动占主导地位。
(3)对称制动压力能够很好降低活塞-卡钳的馈入能量,使制动器的复模态振型以制动盘更高阶的面外振动为主,从而提高复特征频率。可以通过降低传力部件的摩擦损耗和增加活塞与卡钳受压面积的一致程度来提高制动压力的对称性,从而使低频制动尖叫更加难以被激发。
