基于粒子群算法的改进模态参数识别方法

张锦东， 郭小农， 罗晓群， 张玉建， 徐洪俊,2

(1. 同济大学 土木工程学院，上海 200092； 2. 国网江苏省电力工程咨询有限公司，南京 210000)

以研究结构动力特性为目标的振动模态参数识别方法是近年来工程领域的研究热点之一。传统的模态参数识别方法通常基于已知结构的输入和输出实现对模态参数的识别，此类方法受到现场试验条件和结构规模的限制。相对地，另一类基于输出的模态参数识别方法仅根据系统输出进行模态参数识别，在交通、土木、机械、航空航天领域得到了广泛的应用[1]。

基于输出的模态参数识别方法在近几十年来快速发展，环境激励下的基于输出的频域[2]和时域[3-4]模态参数识别方法得到了广泛的应用并取得了良好的效果，此类方法多用于激励近似为白噪音或平稳激励的情况。近年来，一类基于小波变换[5]或Hilbert变换的时频分析方法被应用于基于输出的结构模态参数识别中。Huang等[6]提出的经验模态分解(empirical mode decomposition，EMD)和Hilbert-黄变换(Hilbert-Huang transform,HHT)实现了对复杂信号的瞬时特征提取以及对非平稳信号的分析，但是在处理密集模态结构的频率混叠、窄带信号以及信号间歇性波动等方面仍有不足。Chen等[7]提出的解析模态分解(analytical mode decomposition，AMD)与经验模态分解具有相同的功能，并克服了经验模态分解中存在的不足，在结构模态参数识别中得到一定应用，并成功进行了密集模态结构的模态参数识别[8]。

现有的基于Hilbert变换的结构模态参数识别方法通常将模态试验中处理得到的多模态振动衰减信号进行分离，得到一系列时域单模态衰减信号后进行模态参数识别。此类方法中调用一次或多次Hilbert变换，存在边界效应明显、对噪声敏感、边界分割频率对单分量信号的分离效果影响较大等问题。为此，本文结合奇异值分解、解析模态分解、自回归功率谱和粒子群算法提出了一种可用于密集模态信号在强噪声干扰下的改进模态参数识别方法。

本文首先介绍了基于粒子群算法的改进模态参数识别方法，并改变噪声强度、频率密集程度、阻尼比对模拟多模态振动衰减信号进行参数识别来验证本文方法的有效性，最后采用本文提出的模态参数识别方法对数值模拟结构和实际结构进行模态参数识别。结果表明，本文提出的方法具有较高的识别精度，可实现在强噪声干扰下的大阻尼、密集频率信号的模态参数识别。

1 模态参数识别方法

1.1 奇异值分解降噪

结构模态参数识别前，对信号进行降噪以减小识别误差。奇异值分解方法已被证明在信号降噪中是有效的，并且该方法可用于被白噪声或者有色噪声污染的信号降噪中。此方法的基本原理如下：

假设含有噪声的信号如式(1)所示

y=[y1,y2,y3,…,yn]

(1)

基于相空间重构理论，将式(1)的信号构造为p×q阶Hankel矩阵

(2)

式中，N为信号长度，N=p+q-1，且p≥q。

对Hm进行奇异值分解得到

Hm=UΣVT

(3)

式中，U和VT分别为p×p和q×q矩阵;Σ为式(4)所表达的p×q的对角矩阵

Σ=diag(λ1,λ2,…，λk)

(4)

式中，λ1,λ2,…,λk为矩阵Hm的奇异值，且λ1≥λ2≥…≥λk≥0。

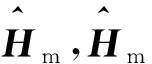
采用奇异值分解降噪的关键问题是选定重构矩阵的维数和有效秩的阶数。工程应用中通常取重构矩阵的维数p=N/2。土木工程结构的自振频率在振动曲线的频响函数中会出现明显的峰值，根据此性质和文献[9]的研究成果，对振动信号进行奇异值分解降噪时可取有效秩的阶数等于源振动信号中主频个数的2倍。

1.2 解析模态分解法

Chen等提出的解析模态分解在处理密集模态结构的频率混叠、窄带信号以及信号间歇性波动等方面比经验模态分解具有更好的效果。该方法结合Hilbert变换实现了结构的模态参数识别和模态参数时变特性分析[10]，具有广泛的应用空间。

0≤ω1<ωb1<ω2<ωb2…<ωi<ωbi<ωi+1…<ωn-1<ωb(n-1)<ωn

(5)

由此，原始信号x(t)可分解为一系列单频信号，分解过程由式(6)和式(7)给出

si(t)=sin(ωbit)H[x(t)cos(ωbit)]-

cos(ωbit)H[x(t)sin(ωbit)],

(i=1,2,3,…,n-1)

(6)

(7)

式中，H[·]为Hilbert变换。

对多个密集频率信号叠加的复杂信号进行模态分解时，解析模态分解法首先构造一对具有相同特定时变频率的正交函数，并将该正交时变函数与原信号的乘积进行Hilbert变换，分解出在频率时间平面内低于正交函数时变频率的任意信号。利用AMD法可将多模态信号分解为一系列只含单模态特征的子信号。

在结构的模态试验中，外界冲击荷载激励下多模态的自由衰减振动响应信号经解析模态分解后可被直接分解为一系列单模态自由衰减振动响应信号；环境激励下的多模态振动响应信号经解析模态分解后可得到一系列单模态特征的子信号，此时可利用随机减量技术消除子信号中随机响应的影响，得到单模态自由衰减响应信号。

采用解析模态分解得到第j阶模态的单频信号xj(t)后，可构造解析信号yj(t)

yj(t)=xj(t)+iH[xj(t)]=Aj(t)·e-iθj(t)

(8)

通过式(8)可得到t时刻的振幅Aj(t)和相位θj(t)。

根据结构动力学理论可知，单模态自由振动衰减响应信号可表示为

A0e-ξjωjtcos(ωd,jt+φj)

(9)

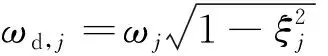
对比式(8)和式(9)，若令

θj(t)=ωd,jt+φj

(10)

则可根据解析信号yj(t)的瞬时相位函数θj(t)按式(11)得到结构第j阶有阻尼固有频率

(11)

同理，对比式(8)和式(9)，可构造对数函数

A(t)=A0e-αjt=A0e-ξjωjt

(12)

则可根据解析信号yj(t)的瞬时振幅函数Aj(t)，拟合得到对数函数A(t)的指数

αj=ξjωj

(13)

对于实际土木工程结构，阻尼比通常小于5%，因此采用有阻尼固有频率ωd,j代替无阻尼固有频率ωj能够满足计算精度要求，则结构的各阶模态阻尼比为

ξj=αj/ωd,j

(14)

由于Hilbert变换导致端部的频率泄露在式(12)的拟合过程中将产生明显误差，在式(5)～式(14)的模态参数识别过程中，Hilbert变换前可采用镜像沿拓[11]抑制Hilbert变换产生的边界效应。

1.3 自回归功率谱

对于离散的振动信号而言，传统的傅里叶变换存在频谱泄露问题，信号中存在的噪声或非平稳部分会导致傅里叶谱出现扭曲。此时可采用不涉及时频转化过程的参数化模型功率谱估计方法替代傅里叶谱。AR模型谱估计是功率谱估计的核心方法，采用AR模型谱代替傅里叶谱可更准确地确定功率谱峰值和解析模态分解的边界分割频率。将AR模型谱与小波变换[12]、解析模态分解[13]等结合，可明显提升模态参数的识别精度。

采用式(15)所示的AR模型表示信号x(n)

(15)

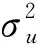
(16)

则信号x(n)的自回归功率谱PAR(ejw)可由式(17)计算

(17)

由于Burg法[14]通过分析观测数据得到需要的模型参数，无需求解计算量较大的自相关函数，下文的AR模型谱估计使用Burg法。

1.4 粒子群算法

基于自回归功率谱选取合理边界分割频率的前提下，采用式(5)～式(14)可较准确地分离信号、识别结构模态参数。实际结构的阻尼通常具有振幅相关性，在实测中不同的结构振幅将导致不同的阻尼比，因此实测振动信号的各单分量模态振动信号带宽并不完全相同。对于阻尼比未知的密集频率信号，解析模态分解中采用相对较窄的边界分割频率可能导致某阶模态信号未完全被截取，而采用相对较宽的边界分割频率可能会截取到相邻模态信号和较多噪声信号。选取不合适的边界分割频率将导致分解出的时域曲线的形状畸变，影响模态参数识别结果。针对此，采用粒子群优化(particle swarm optimization，PSO)算法AMD方法中的边界分割频率来得到最优化的振动衰减曲线，以进一步识别结构的自振频率和阻尼比。

PSO-AMD的联合模态参数识别方法如下。首先根据振动信号的自回归功率谱图采用峰值拾取法确定结构前D阶有阻尼自振频率ω=[ω1，ω2，…,ωD]T。然后建立一个D维搜索空间，该空间中有n个粒子组成的种群D=(D1,D2,…,Dn)。种群中的第i个粒子代表一个D维向量Di=[di1,di2,…,diD]T，该向量中的元素dij则代表第i个粒子中结构第j阶模态的边界分割频率截断带宽。由此可确定AMD方法的边界分割频率可表示为

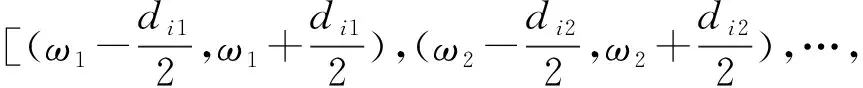
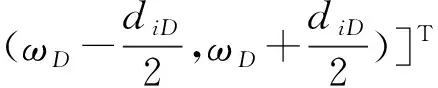
(18)

各粒子的适应度值可由解析模态分解分离所得的信号xj(t)和剔除此信号的其余信号xk(t)=x(t)-xj(t)的相关系数计算得出。若xj(t)被完全分离，则xj(t)和xk(t)的相关系数最小。每个粒子的适应度值均可表示为Ri=[Ri1,Ri2,…,RiD]T，该粒子的对应速度为Vi=[Vi1,Vi2,…,ViD]T，对应个体极值为Pi=[Pi1,Pi2,…,PiD]T，此种群的全局极值为Pg=[Pg1,Pg2,…,PgD]T。

迭代过程中，粒子更新速度和位置更新公式如式(19)和式(20)所示

(19)

(20)

式中：w为惯性权重；k为迭代次数；c为加速度因子；r为分布于[0,1]的随机数。

尽管在密集频率信号的模态参数识别中可以不断人为调整AMD方法的截断频率分解出完整的单模态信号，得到准确的识别结果，然而由于事先并不确定最优化的边界分割频率，这类调整可能影响最终识别结果。将PSO方法与AMD方法结合，使边界分割频率可自适应地调整，从而提升识别效率和识别精度。

1.5 模态参数识别步骤

综合1.1节～1.4节，对多模态振动衰减曲线的模态参数识别方法步骤如下：

步骤1根据振动曲线的自回归功率谱确定振动信号的主频数i和初始边界分割频率，根据主频数确定奇异值分解阶数2i，采用奇异值分解对信号进行降噪处理；

步骤2调用1.4节中的粒子群优化算法确定前j阶单模态振动曲线的最优边界分割频率，优化目标为分离所得单模态信号与原信号中剔除该信号所得的信号相关度最低；

步骤3采用步骤2中的最优边界分割频率调用解析模态分解法获取单模态衰减曲线并进行模态参数识别，获取结构前j阶阻尼比、自振频率。

基于Hilbert变换的模态参数识别方法对噪声敏感，较强的噪声影响模态参数的识别结果。受外界环境的干扰，实际模态试验中采集的信号信噪比可能较低，识别效果不佳。本文提出的方法理论上可实现低信噪比下白噪声或有色噪声信号的降噪，将PSO方法和AMD方法结合可自适应地对边界分割频率进行调整，提升模态参数识别精度。

2 模拟信号模态参数识别

结构模态试验中一类常见的测试方法是对结构施加一定的激励后获取结构的自由衰减振动响应，对自由衰减振动曲线进行模态参数识别。为了验证本文提出的模态参数识别方法的有效性，构造式(21)所示的振动衰减信号进行模态参数识别

(21)

下文分别改变噪声强度、频率密集程度和信号阻尼比，采用了三种方法进行信号的模态参数识别：方法1——仅采用解析模态分解法进行信号分离，对单模态信号进行识别，边界分割频率按Chen等的研究取两个主频信号的二分位置；方法2——利用粒子群算法优化边界分割频率后，采用解析模态分解法进行信号分离，对单模态信号进行识别；方法3——采用本文提出的模态参数识别方法进行模态参数识别。

2.1 不同噪声强度下模态参数识别

按照式(21)形式给出一条包含三个主频、时长为50 s、采样频率100 Hz的模拟振动衰减信号(单位mV)，模拟振动衰减信号的主要参数，如表1所示。在此衰减信号中加入不同强度的白噪声，使信噪比(signal-to-noise ratio,SNR)分别为-6 dB，-2 dB，2 dB，6 dB，10 dB。图1中仅展示在-6 dB信噪比下振动衰减时程曲线、自回归功率谱和采用方法3分离的单模态衰减振动曲线。

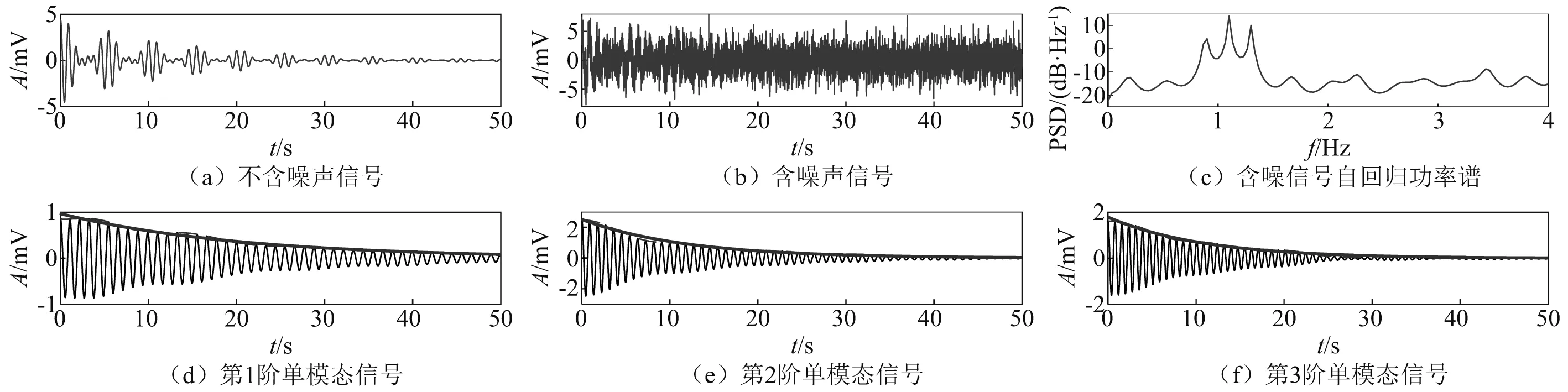
图1 原信号和单模态信号Fig.1 Original signal and single mode signal

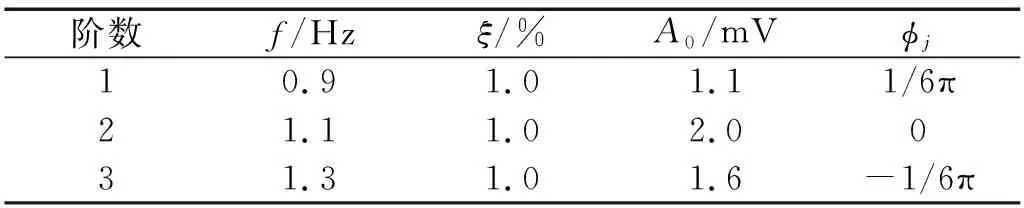
表1 模态参数理论值Tab.1 Theoretical values of modal parameters

采用方法1、方法2、方法3识别得到的自振频率和阻尼比识别结果，如表2所示。自振频率和阻尼比的识别误差折线图，如图2所示，图例中1-2代表采用方法1对第2阶模态参数的识别误差，依次类推。图2中，三种方法对自振频率的识别结果误差均保持在5%以内；方法1和方法2在信噪比小于-2 dB时对阻尼比的识别产生了超过10%的误差，较强的噪声影响了单模态信号的分离效果；方法3在信噪比为-6 dB的强噪声环境中仍保持了较高的阻尼比识别精度。在信噪比大于6 dB时三种方法的识别误差相近。

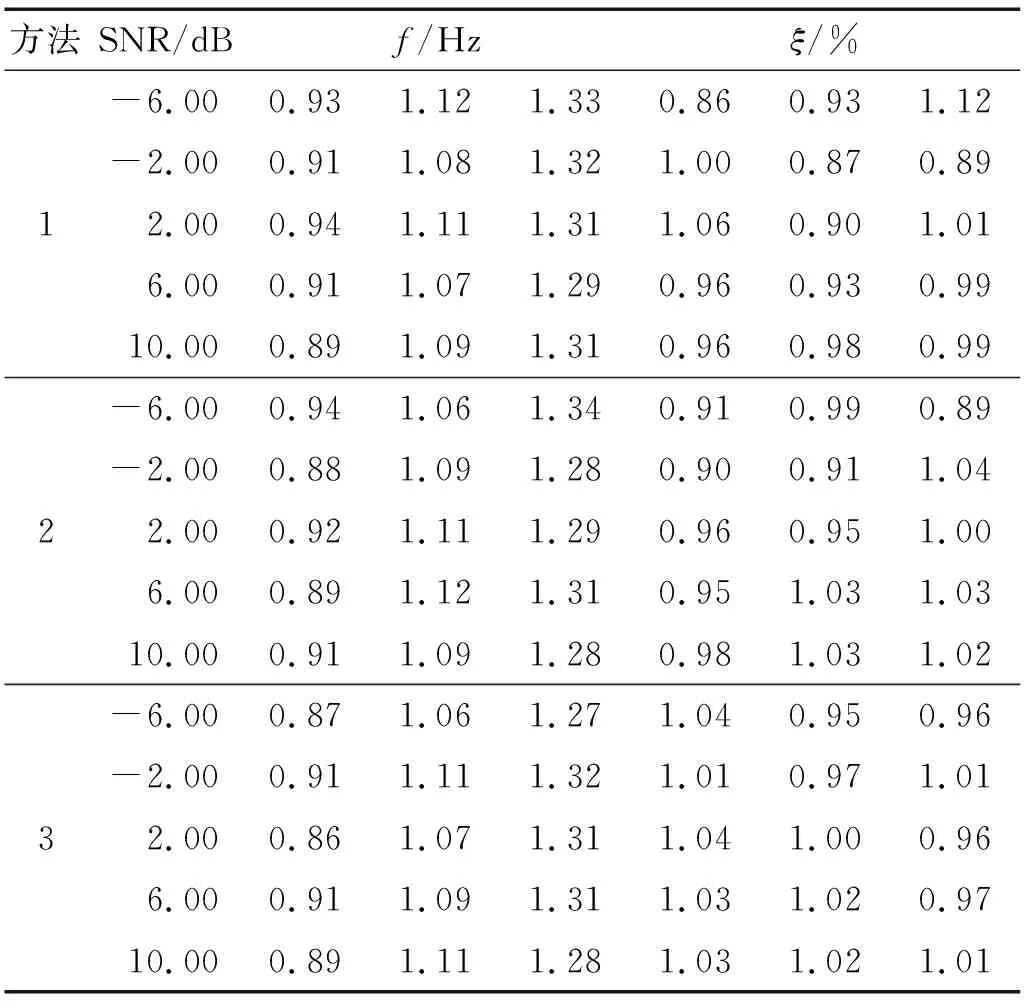
表2 模态参数识别结果Tab.2 Identification results of modal parameters

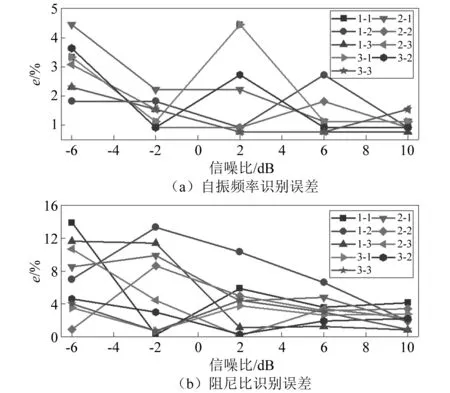
图2 模态参数识别误差Fig.2 Error of modal parameter identification

对图1(a)的振动衰减信号添加有色噪声，验证在有色噪声干扰下本文方法的识别效果。有色噪声由强度为20 dB的高斯白噪声ξ1(n)和幅值为2 mV的白噪声ξ2(n)按式(22)组合而成

(22)

将式(22)的有色噪声加入表1的振动衰减曲线中，有色噪声信号、含色噪声信号、自回归功率谱和方法3分离的单模态衰减信号，如图3所示。对含有色噪声的衰减信号识别结果和误差，如表3所示。表3中，方法3自振频率和阻尼比的识别误差均小于5%，在较强有色噪声干扰下本文提出的方法依然可以较好地实现模态参数的识别精度。

图3 原信号和单模态信号Fig.3 Original signal and single mode signal

表3 模态参数识别结果Tab.3 Identification results of modal parameters

2.2 不同阻尼比下模态参数识别

保持振动衰减信号的自振频率f、初始振幅A0和相位φ与表1相同；并在信号中加入高斯白噪声，保持信号信噪比为2 dB。分别取各阶模态阻尼比为0.5%，1%，2%，3%，4%，以验证不同阻尼比下模态参数识别效果。限于篇幅，图4中仅展示在模态阻尼比为4%时的振动衰减时程曲线、自回归功率谱和采用方法3分离的单模态衰减振动曲线。

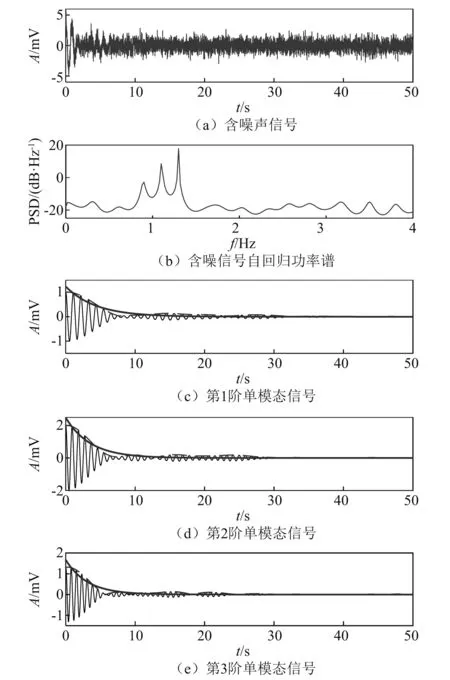
图4 原信号和单模态信号Fig.4 Original signal and single mode signal

采用方法1、方法2、方法3的自振频率和阻尼比识别结果，分别如表4和表5所示。自振频率和阻尼比的识别误差折线图，如图5所示，图中1-2代表采用方法1对第2阶模态参数的识别误差，依次类推。图5中，三种方法对自振频率的识别误差相差不大，均保持在4%以内。随着阻尼比的增加，各个方法对于阻尼比的识别误差均呈现增大趋势，这是由于振动曲线衰减较快导致拟合衰减曲线的数据点不足。相对而言，本文提出的方法3对于阻尼比识别精度高于方法1和方法2，误差保持在5%以内。当衰减信号阻尼较大(>3%)时，方法3也可较准确地识别大阻尼衰减信号的模态参数。

表4 自振频率识别结果Tab.4 Identification results of natural frequency

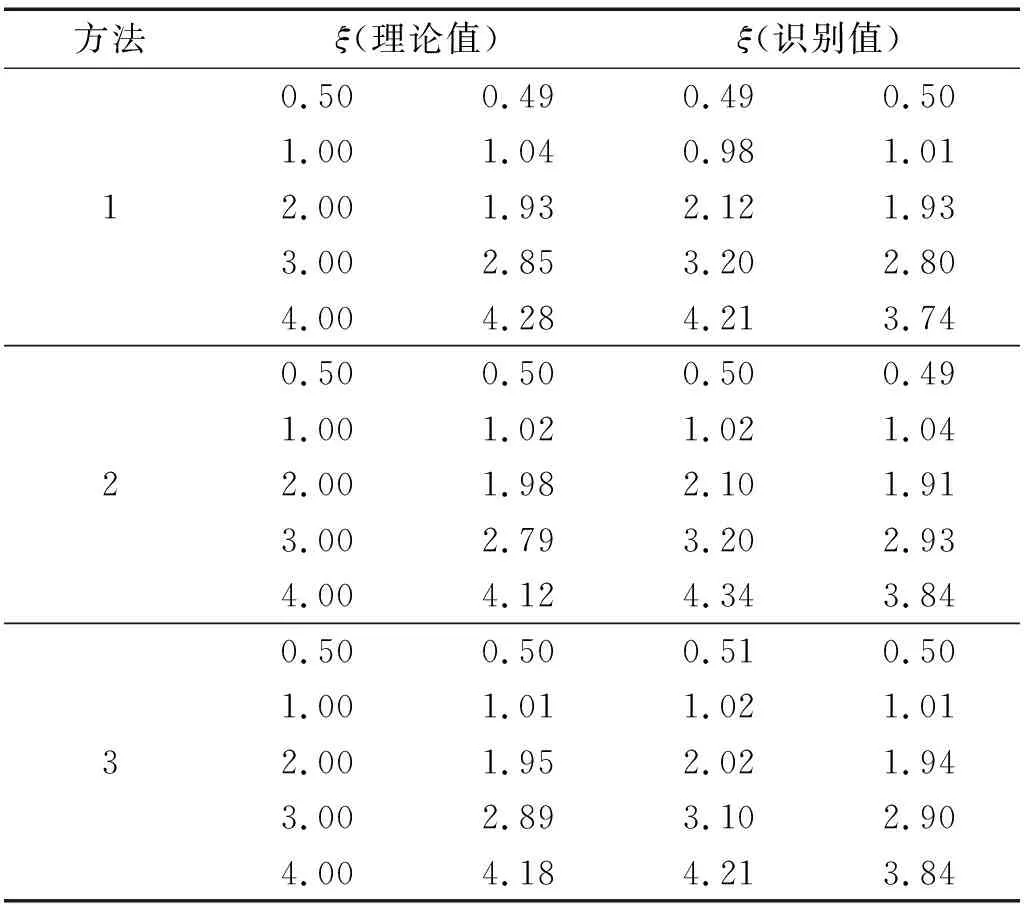
表5 阻尼比识别结果Tab.5 Identification results of damping ratio %

图5 模态参数识别误差Fig.5 Error of modal parameter identification

2.3 不同频率密集度下模态参数识别

在振动衰减曲线中加入高斯白噪声，保持信号信噪比为2 dB，判断不同频率密集度下模态参数识别效果。频率密集度δ=(fi-fi-1)/(fi+fi-1)[15]。衰减曲线的各阶自振频率和阻尼比，如表6所示，初始振幅A0和相位φ与表1相同。图6中仅展示在δ=0.03时的振动衰减时程曲线、自回归功率谱和采用方法3分离的单模态衰减振动曲线。

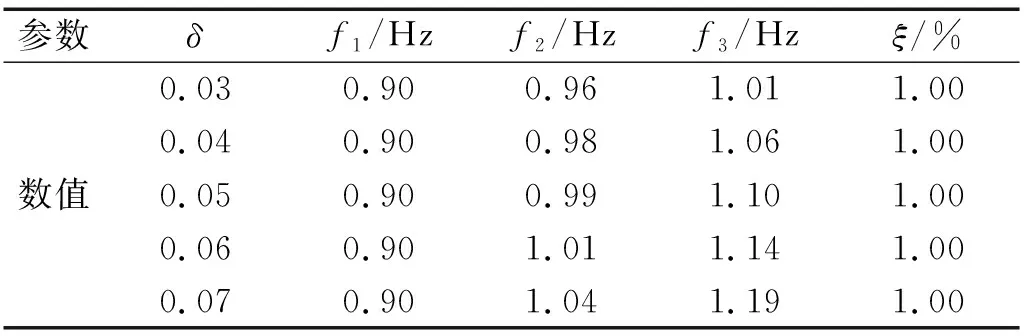
表6 模态参数理论值Tab.6 Theoretical values of modal parameters

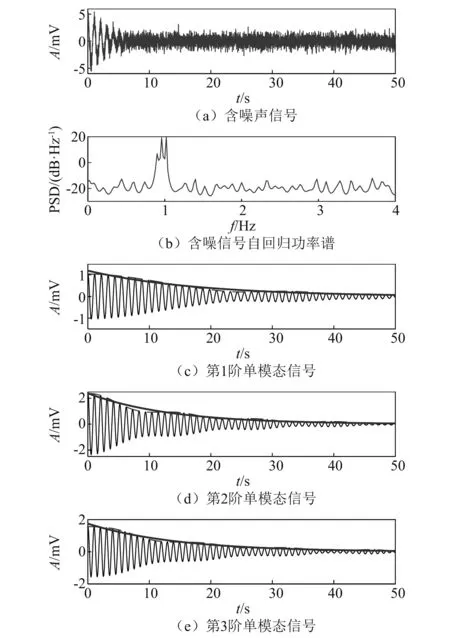
图6 原信号和单模态信号Fig.6 Original signal and single mode signal

采用方法1、方法2、方法3的自振频率和阻尼比识别结果，如表7所示。自振频率和阻尼比的识别误差折线图，如图7所示，图中1-2代表采用方法1对第2阶模态参数的识别误差，依次类推。图7中，当频率较为密集时，两个模态间的相互影响作用增强，各个方法的分离效果下降，误差增加，随着频率密集程度的减小，自振频率和阻尼比的识别误差减小。本文提出的方法在密集度δ=0.03时对自振频率和阻尼比的识别误差仍保持在4%以内，实现了较准确的识别。

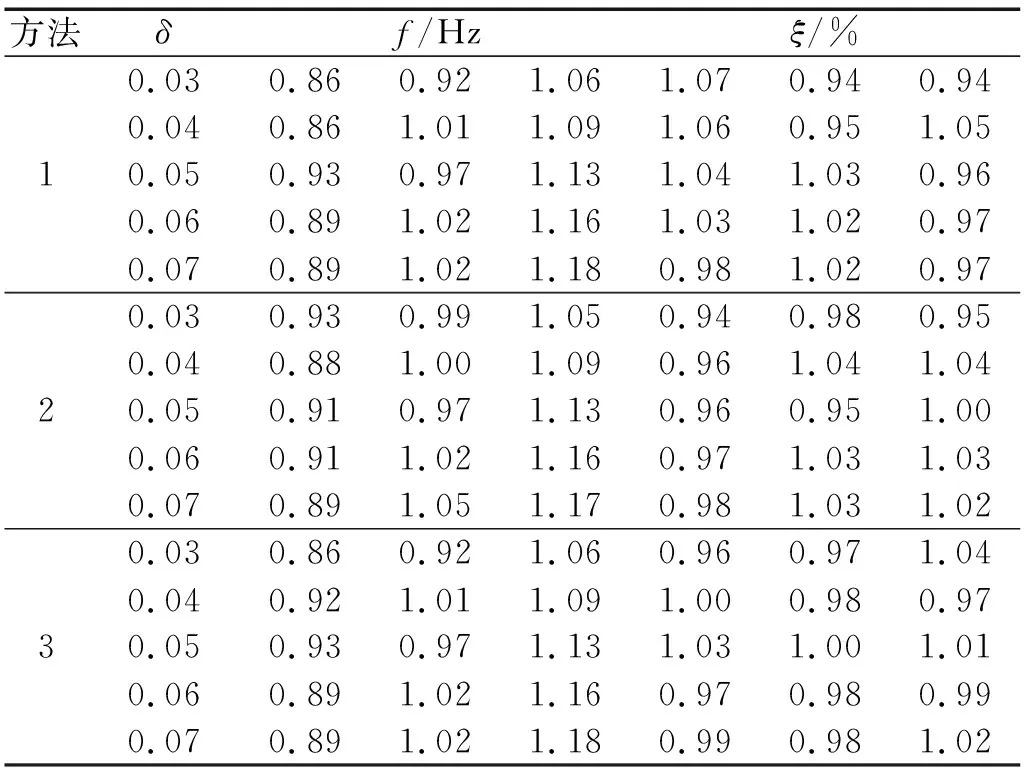
表7 模态参数识别结果Tab.7 Identification results of modal parameters

图7 模态参数识别误差Fig.7 Error of modal parameter identification

3 结构模态参数识别

3.1 三自由度系统模态参数识别

建立一个图8所示的三自由度弹簧-质量系统，弹簧刚度和质点质量如表8所示。数值模拟采用有限元分析软件ANSYS19.0，采用Rayleigh阻尼模拟系统的阻尼特性，Rayleigh阻尼系数α=0.010 62，β=0.002 04。在0时刻对质点3施加1 000 kN的冲击荷载，并在响应曲线中加入式(22)形式的有色噪声，其中高斯白噪声ξ1(n)强度为-150 dB，白噪声ξ2(n)幅值为10-6m/s2。质点1的有噪声响应曲线、自回归功率谱、前3阶单模态响应曲线，如图9所示。

图8 三自由度弹簧-质量系统Fig.8 Three degree of freedom spring-mass system

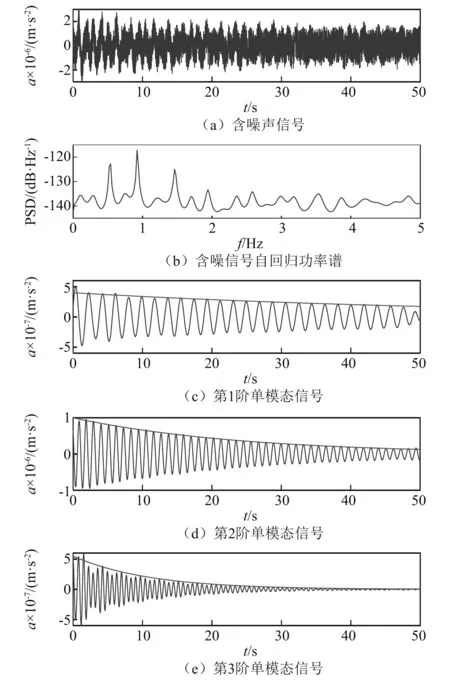
图9 原信号和单模态信号Fig.9 Original signal and single mode signal

表8 弹簧刚度和质点质量Tab.8 Spring stiffness and mass of particles

三自由度弹簧-质量系统自振频率与阻尼比的理论值、识别值和识别误差(以Ef和Eξ表示)如表9所示。表9中，自振频率和阻尼比的识别误差≤2%，本方法在较大有色噪声干扰下仍取得了较好的识别效果。

表9 模态参数识别结果Tab.9 Identification results of modal parameters

3.2 球面空间网格结构模态参数识别

对图10所示的球面空间网格结构进行激励并采集节点的振动响应。测试人员在节点跳跃对结构施加近似的竖向冲击荷载，同时采集节点的竖向振动响应。激励点位置和采集点位置,如图11所示。测试中，在A1点施加竖向激励，同时在1点采集节点响应，依次进行至在A10点施加竖向激励，同时在10点采集节点响应，共采集10条振动衰减曲线。由于测试中外界环境和结构附加设备的运行对结构造成影响，采集到的振动衰减响应曲线信噪比较低，采用本文的模态参数识别方法对响应曲线进行识别。

图10 球面空间网格结构Fig.10 Spherical reticulated spatial structures

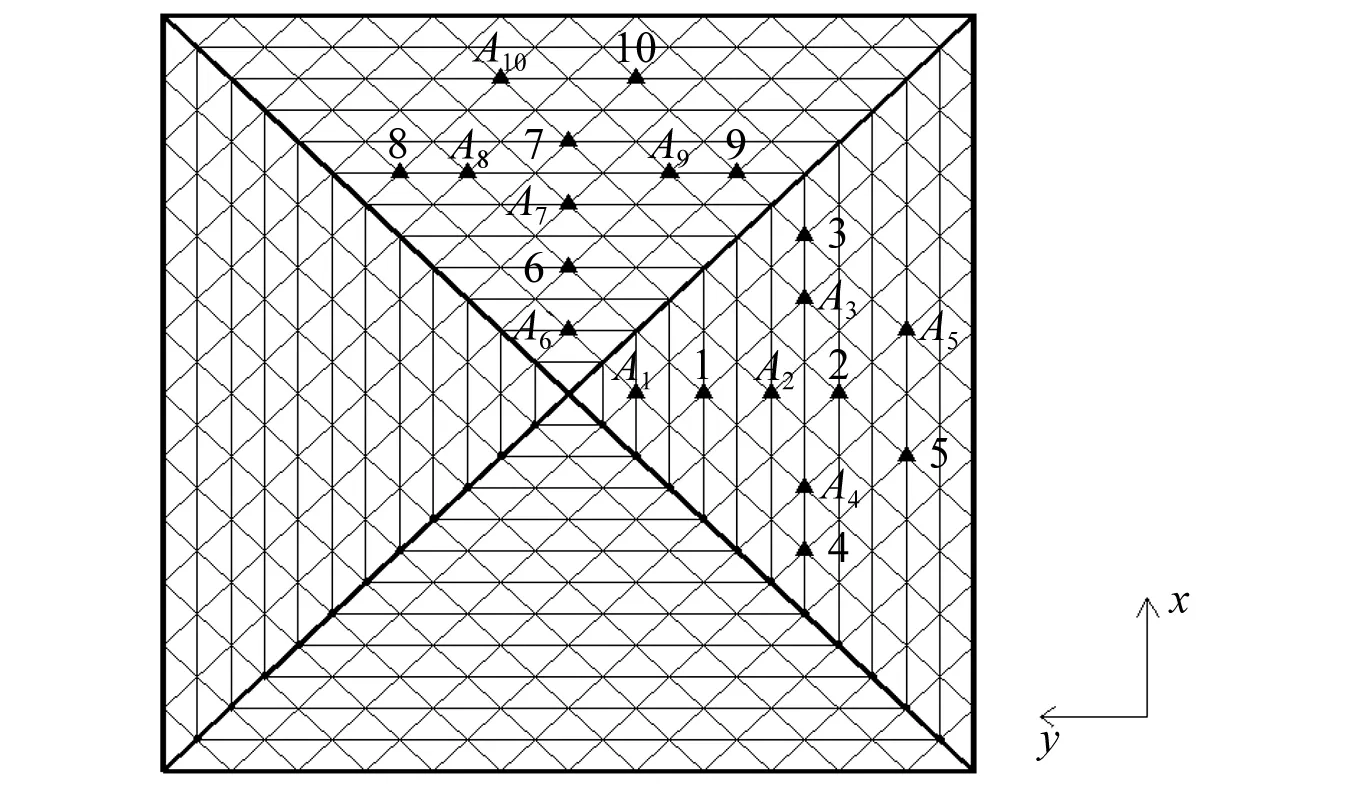
图11 激励点和采集点Fig.11 Excitation positions and collection positions

采集点1处的振动响应曲线、自回归功率谱、采用本文模态参数识别方法得到的结构前6阶单模态响应曲线，如图12所示。依次对10条振动衰减曲线进行识别，各振动衰减曲线的前6阶自振频率和模态阻尼比如表10所示。表11给出了文献[16]中此结构的前6阶自振频率和模态阻尼比均值，采用本文方法识别的自振频率均值和模态阻尼比均值同时列于表11。表11中本文方法的识别结果与罗晓群等的识别结果基本一致，本文方法可在较低信噪比下识别密集频率结构的自振频率和阻尼比。

表10 曲线1～10模态参数识别结果Tab.10 Modal parameter identification results of curve 1-10

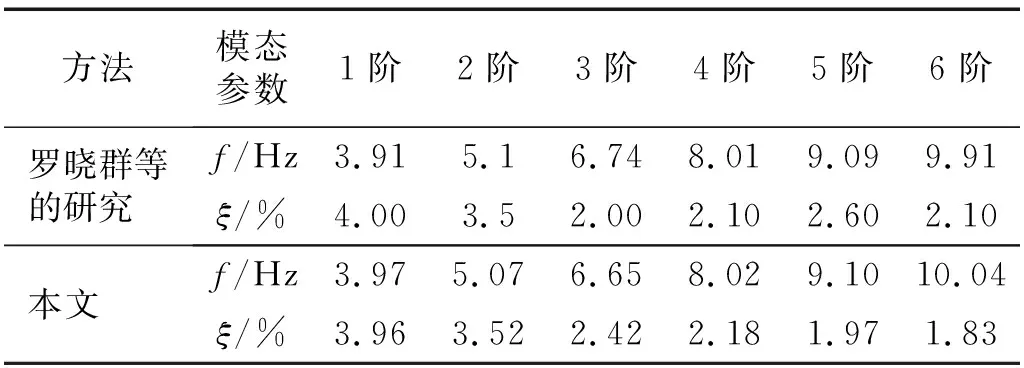
表11 模态参数识别结果均值Tab.11 Mean value of modal parameter identification results

4 结 论

本文针对多模态振动衰减信号的模态参数识别，提出了一种基于粒子群算法的改进模态参数识别方法，改善了现有的基于Hilbert变换的模态参数识别方法存在的边界效应明显、对噪声敏感、边界分割频率对单分量信号的分离效果影响较大等问题，可用于强噪声干扰下密集频率、大阻尼信号的模态参数识别，并通过数值算例和现场测试验证了本文提出方法的有效性。得到结论如下：

(1) 现有的基于解析模态分解的传统方法仅可实现较高信噪比条件下(>6 dB)的模态参数识别，本文提出的识别方法可实现在低信噪比(-6 dB)、有色噪声环境下的模态参数准确识别，具有更广泛的应用范围。

(2) 随着阻尼比增加，振动曲线衰减较快导致拟合衰减曲线的数据点不足，基于衰减曲线的识别方法对阻尼比的识别精度呈现下降趋势，将信号准确分离是实现具有较大阻尼比衰减信号的模态参数识别的关键。

(3) 随着频率密集度的增加，各模态的相互影响作用增强，阻尼比和自振频率的识别精度呈现下降趋势。边界分割频率明显影响密集频率信号的模态参数识别效果。本文提出的方法可寻找最优边界分割频率，将各单模态信号准确分离和识别。

(4) 本文提出的方法可用于低信噪比环境下结构的模态参数识别。