水下单信标导航算法研究及置信区间分析

2022-02-16王燕张新宇孙思博付进

哈尔滨工程大学学报 2022年1期

王燕，张新宇，孙思博，付进

(1.哈尔滨工程大学水声技术重点实验室，黑龙江哈尔滨 150001； 2.海洋信息获取与安全工业和信息化部重点实验室(哈尔滨工程大学)，黑龙江哈尔滨 150001； 3.哈尔滨工程大学水声工程学院，黑龙江哈尔滨 150001； 4.青岛海纳水下信息技术有限公司，山东青岛 266400)

单信标导航技术根据所利用的声波信号测量信息的不同可分为2类，第1类获取声波信号的传播时延信息(time of arrival，TOA)求解目标的位置[1-7]。De Palma 等[8]建立了单信标问题中以传播时延为观测量的二阶运动模型，并分别利用状态增补技术和可观测性矩阵的秩判据对系统的可观测性进行了分析，指出了不可观测轨迹。曹俊等[9]针对AUV在直线轨迹下的单信标定位进行了研究，利用虚拟长基线的概念对单信标定位系统进行了仿真实验，实验结果表明在虚拟阵列中信标的标定精度及AUV的轨迹与水下应答器的垂直距离对单信标定位系统的最终定位精度有很大影响。孙思博等[10]建立了一种单AUV发射信号多AUV接收信号的SIMO模型(single-input-multiple-output model)，相比传统的单信标多AUV定位模型，该模型可以在2个信号周期内完成对多AUV的同时定位并获得更高的定位精度。Fallon等[11]基于传播时延信息建立了一种水面航行器和AUV的协同导航机制，通过规划水面航行器的航行路径以配合AUV完成自身位置的求解。

水下自主航行器(autonomous underwater vehicle，AUV)是探索和开发海洋的重要运载平台之一，因其具有无人、无缆且自主航行的特点，故适合完成长期、可规划或者具有危险性的工作，在资源勘测、海底绘图、海洋环境监测和水下设施检修等领域发挥着巨大作用，高精度的位置信息是AUV完成这些任务的关键[1-3]。常见的水下声学导航方法根据声信标数量和基线长短的不同可分为以下几类：长基线(long baseline，LBL)[4]、短基线(short baseline，SBL)、超短基线(ultra-short baseline，USBL)[5]和单信标导航。相比其他的声学方法[6-7]，单信标导航技术因具有布放简单和成本低的优点而受到广泛关注。

第2类获取声波信号入射的方位角信息(direction of arrival，DOA)求解目标的位置。李佳橦等[12]提出了一种基于单信标纯方位信息测量的AUV定位方法，构建了2-DOF(degree of freedom)姿态的AUV定位问题模型并采用EKF(extented Kalman filter)进行求解，仿真结果表明相比于测距信息观测模型，纯方位定位在滤波精度和收敛性上有优势。Becker等[13]在声信标入水深度已知的前提下通过测量方位角信息对AUV和声信标的位置坐标进行同步求解。刘开华等[14]提出了一种在非均匀媒质中联合到达时间(TOA)和到达角度(DOA)浅海多径环境下的定位算法，该算法不仅能够克服声速变化引起的路径弯曲问题，还可以减少海水流动对节点拓扑结构产生的影响。

本文首先介绍了3种典型的水下单信标导航算法，包括基于时延信息的单信标导航算法、基于方位角信息的单信标导航算法以及联合使用时延和方位角信息的单信标导航算法。水平位置精度因子(horizontal dilution of precision，HDOP)或圆概率误差(circular error probability，CEP)等一维参数仅能定量地描述上述方法的导航精度，但不能给出导航误差整体分布的细节，本文分析并比较了这3种典型的单信标导航方法置信区间的分布。本文基于偏微分矩阵建立了3种方法的导航误差和各测量误差的关系式，在此基础上利用导航误差的协方差矩阵分析了时延测量误差和方位角测量误差对3种方法的导航结果置信区间分布的影响，并从水平位置精度因子和置信椭圆的形状2个角度对3种方法置信区间进行了比较[15-16]。文中研究可为单信标导航中导航点的选取以及不同方法的导航结果的数据融合提供理论参考。

1 3种典型的单信标导航算法

单信标导航的几何示意图如图1所示，声信标固定于O点且周期性地发射声信号，AUV从A点走到B点并接收声信标所发射的声信号，以O点为原点建立二维直角坐标系，X轴指向正东方向，Y轴指向正北方向。

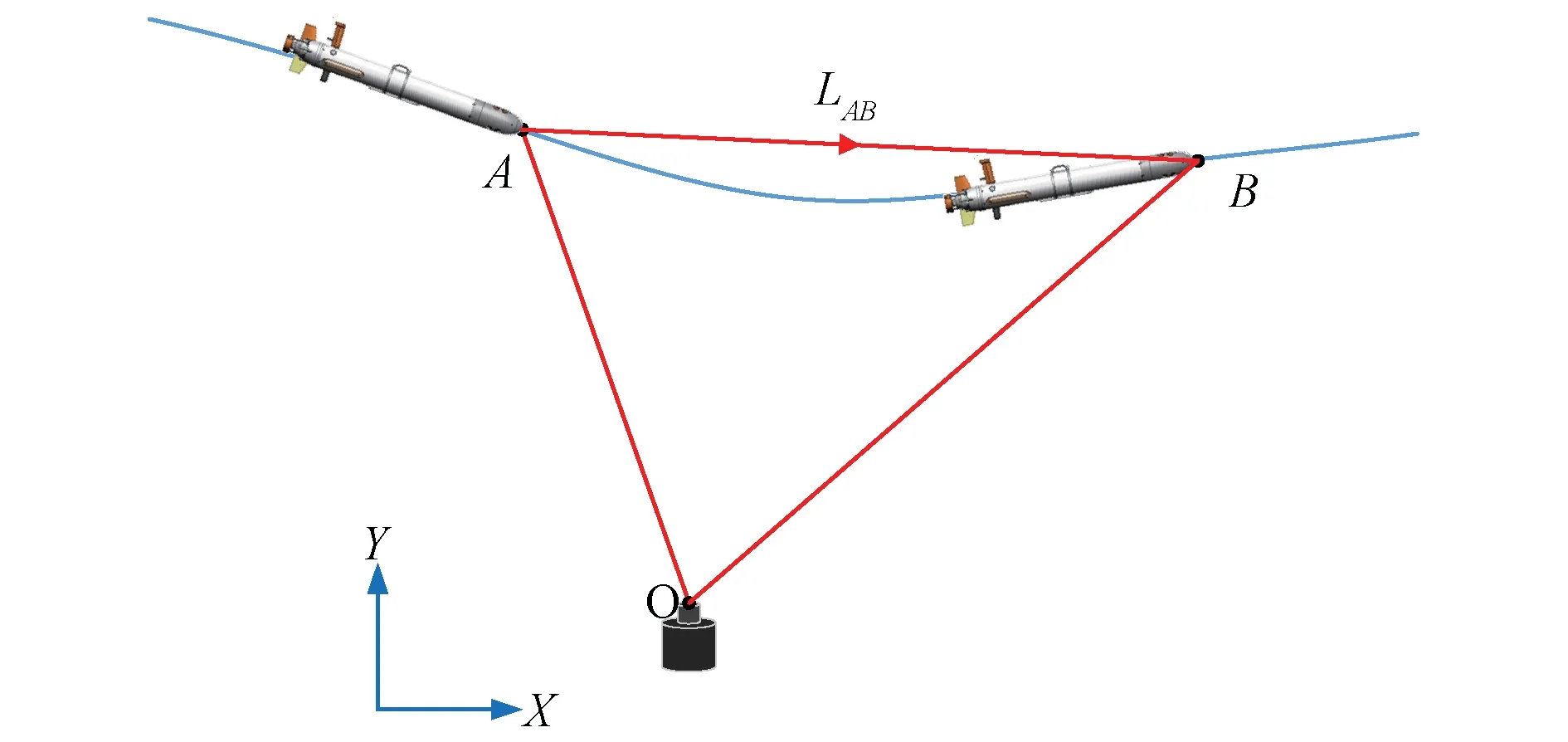
图1 单信标导航的系统模型

在该导航模型中可以获得以下的先验信息：

1) 声信号从O点到达A点和B点的传播时延tA和tB可测；

2) 声信号在A点的入射方向和X轴的夹角(即向量OA和X轴的夹角)φA可测，同理可获得φB；

3) AUV从A点到B点的虚拟基线矢量L=[xAByAB]可通过AUV搭载的惯性导航系统(inertial navigation system，INS)获得；

4) 声信号在水介质中的传播速度c可通过声速仪进行测量;

5) 星站节点为潜标模式，信标位置已经过校准，校准精度满足导航需求。

接下来介绍3种典型的单信标导航算法，分别是基于时延信息的单信标导航算法、基于方位角信息的单信标导航算法以及联合使用时延和方位角信息的单信标导航算法，为了简便，依次简记为TOA法、DOA法和TOA-DOA法。

1.1 TOA法

TOA法利用AUV在A和B点所接收声信号的传播时延信息建立导航方程以对AUV在X-Y坐标系下B点的坐标进行求解。设O点、A点和B点的坐标分别为(xO,yO)、(xA,yA)和(xB,yB)，则TOA法的导航方程为：

(1)

在实际情况中，由于时延测量误差、声速测量误差、惯导测量误差和声信标位置测量误差的存在，由TOA法得到的B点坐标与真值相比存在偏差，接下来建立导航误差和各测量误差的数学关系式，对式(1)中的前2个等式左右两侧同时取微分得：

(2)

式中|L|为向量L的模长。为了便于分析，将式(2)改写为：

(3)

式中MTOA和NTOA可写为：

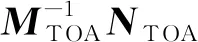
(4)

1.2 DOA法

DOA法利用AUV在A和B两点所接收声信号的方位角信息建立导航方程以对AUV在B点的坐标进行求解，基于所获取的先验信息，DOA法的导航方程为：

(5)

在实际情况中，由于方位角测量误差、声信标位置测量误差和惯导测量误差的存在，由DOA法所获取的B点坐标与真值相比存在偏差，仿照1.1节建立导航误差和各测量误差的数学关系式，其结果为：

(6)

式中MDOA、NDOA和DDOA的表达式为：

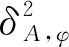
1.3 TOA-DOA法

TOA-DOA法利用AUV在B点所接收声信号的传播时延信息和方位角信息建立导航方程以对AUV在B点的坐标进行求解，基于所获取的先验信息，TOA-DOA法的导航方程为：

(7)

在实际情况下，由于时延测量误差、方位角测量误差、声信标位置测量误差以及声速测量误差的存在，由TOA-DOA法所求解的B点坐标与真值相比存在偏差，仿照1.1节建立导航误差和各测量误差的数学关系式，其结果为：

(8)

式中MTD、NTD和DTD的表达式为：

1.4 二维高斯分布的置信椭圆

置信椭圆代表二维高斯分布的等值轮廓线，并将一个2-D置信区间可视化，以一个95%置信度的置信椭圆为例，它所定义的区域包含了总体中95%的样本。接下来给出误差椭圆的绘制方法。

设一个均值为零的二维高斯分布的协方差矩阵为G，对G进行特征值分解并对特征向量进行正交单位化，其结果为：

(9)

式中：λ1和λ2是G的2个特征值；v1∈R2×1是λ1的特征向量；v2∈R2×1是λ2的特征向量。在本文中，置信椭圆的中心位于所求B点坐标的真值处，该椭圆的长半轴的大小a和短半轴的大小b分别为：

(10)

式中s是一个与置信度有关的量，当置信度分别为99%、95%和90%，s的取值分别为9.210、5.991和4.605。置信椭圆的长轴平行于较大的特征值所对应的特征向量，置信椭圆的短轴平行于较小的特征值所对应的特征向量。本文中所绘制的置信椭圆的置信度皆为95%，后文不再赘述。

2 3种导航算法置信区间的分析

由第1节分析可知，当各测量误差相互独立且服从均值为零的高斯分布时，导航误差服从均值为零的二维高斯分布，在这种情况下，导航误差的协方差矩阵就可以描述导航误差的整体分布情况(置信区间的分布)。本部分基于导航误差的协方差矩阵对3种方法置信区间的分布进行分析。

为了体现A、B和O点的相对几何位置关系，对图1所示的单信标导航模型进行如图2所示的化简。线段AB平行于X轴，O点到线段AB的垂直距离为ρ，线段OA和OB与Y轴的夹角分别为θA和θB，当点A(或B)位于Y轴左侧时，θA(或θB)为负值，反之为正。此时A和B两点的坐标可以表示为：

(11)

本节接下来基于图2所示模型对上述3种方法的导航误差的协方差矩阵进行化简及分析。在实际情况下，相比于其他测量误差，一般时延测量误差和方位角测量误差对导航误差的贡献最大，故本部分只考虑时延测量误差和方位角测量误差对导航结果的影响，此时第1节中的NTOA、NDOA和NTD皆只保留前2列。

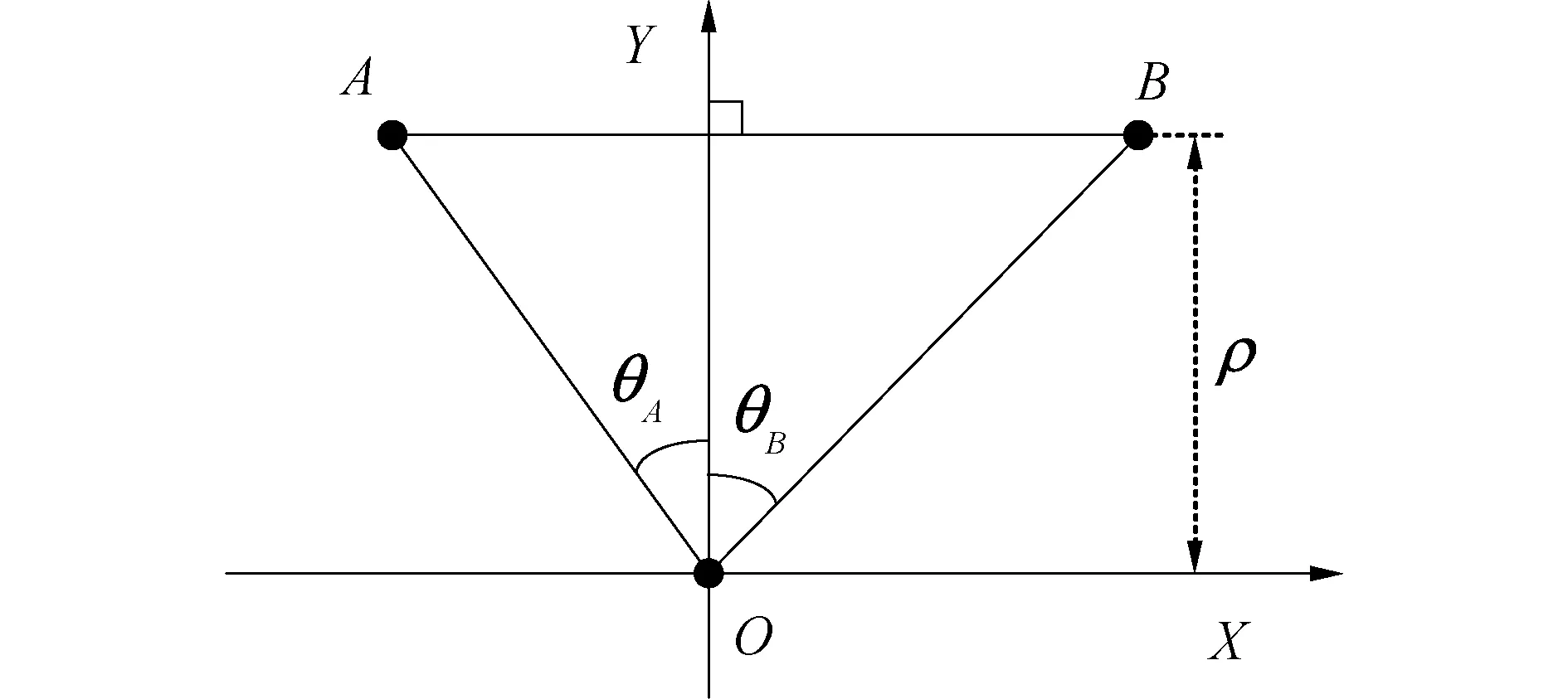
图2 图1所示模型的化简

2.1 TOA法的误差分析

本节对TOA法的导航误差的协方差矩阵进行分析，将式(11)代入1.1节的MTOA和NTOA的表达式中可得：

可以看出，当A和B2点与声信标O共线时，MTOA不可逆，这意味着该系统在此种情况下不可观测。将MTOA和NTOA代入式(4)表达式，则TOA法的导航误差的协方差矩阵可写为：

(12)

其中：

式中：QA(或QB)为正交单位矩阵；QA(或QB)的第1个列向量描述的是与向量OA(或OB)相垂直的方向，其第2个列向量描述的是与向量OA(或OB)相平行的方向。从式(12)可以看出，对于TOA法，A点的时延测量误差会使得导航结果在与向量OB相垂直的方向上产生偏差且该偏差满足均值为零且方差为λA,t的高斯分布，但该测量误差不会使导航结果在与向量OB相平行的方向上产生偏差；B点的时延测量误差会使得导航结果在与向量OA相垂直的方向上产生偏差且该偏差满足均值为零且方差为λB,t的高斯分布，但该测量误差不会使导航结果在与向量OA相平行的方向上产生偏差。

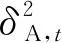
(13)

其中

ΛTOA=diag(λA,t(cos(θB-θ))2+

λB,t(cos(θA-θ))2,0)+

diag(0,λA,t(sin(θB-θ))2+λB,t(sin(θA-θ))2)

式中的θ可以通过式(14)进行求解：

λA,tsin(2(θB-θ))+λB,tsin(2(θA-θ))=0

(14)

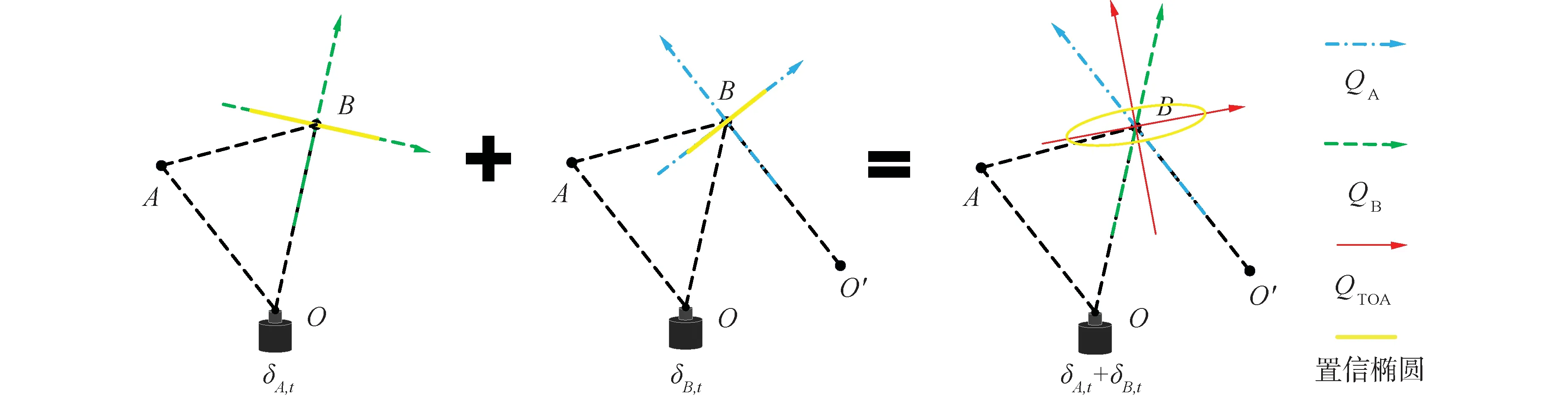
图3 TOA法的置信椭圆

为了对以上结论进行验证，本小节给出了如下的仿真实验，实验参数如表1所示，蒙特卡洛次数为500次。实验结果如图4所示，可以看出当只有A点的时延测量误差存在时，圆圈散点分布在与向量OB相垂直的直线上，当只有B点的时延测量误差存在时，圆圈散点分布在与向量O′B相垂直的直线上，当A和B2点的时延测量误差皆存在时，圆圈散点分布在一个2-D区域内。该仿真实验证明了以上结论的正确性。接下来分析2种特殊情况。

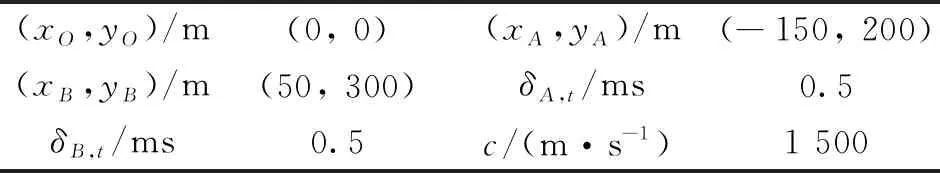
表1 TOA法的实验参数

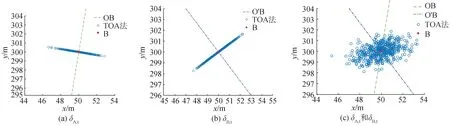
图4 TOA法的仿真实验结果

1) 当cδA,t=cδB,t=λt时，θ的取值等于(θA+θB)/2，cδA,t表示A点的时延测量偏差在A点平行于OA的方向上所对应的距离偏差，cδB,t表示B点的时延测量偏差在B点平行于OB的方向上所对应的距离偏差，也就是说当这2个距离偏差相等时，图3中的实线箭头恰好位于另外2个箭头中间，此时GTOA为：

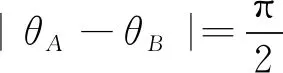
2.2 DOA法的误差分析

本小节对DOA法的导航误差的协方差矩阵进行分析。将式(11)代入1.2节的MDOA和NDOA的表达式中可得：

可以看出，当A和B两点与声信标O共线时，MDOA不可逆，这意味着该系统在此种情况下不可观测。将MDOA和NDOA代入式1.2节GDOA的表达式，则DOA法的导航误差的协方差矩阵可写为：

(15)

式中：

式中：ρA表示线段OA的长度；ρB表示线段OB的长度；QA和QB的细节及含义与2.1节相同。从式(18)可以看出，对于DOA法，A点的方位角测量误差会使得导航结果在与向量OB相平行的方向上产生偏差且该偏差满足均值为零且方差为λA,φ的高斯分布，但该测量误差不会使导航结果在与向量OB相垂直的方向上产生偏差；B点的方位角测量误差会使得导航结果在与向量OA相平行的方向上产生偏差且该偏差满足均值为零且方差为λB,φ的高斯分布，但该测量误差不会使导航结果在与向量OA相平行的方向上产生偏差。

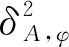
(16)

式中：

ΛDOA=diag(λA,φ(sin(θB-θ))2+

λB,φ(sin(θA-θ))2,0)+

diag(0,λA,φ(cos(θB-θ))2+λB,φ(cos(θA-θ))2)

式中

λA,φsin(2(θB-θ))+λB,φsin(2(θA-θ))=0

(17)

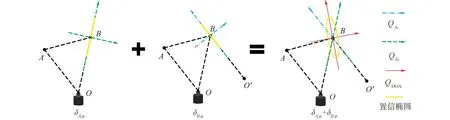
图5 DOA法的置信椭圆

为了对以上结论进行验证，本小节给出了如下的仿真实验，实验参数如表2所示，蒙特卡洛次数为500次。实验结果如图6所示，可以看出当只有A点的方位角测量误差存在时，圆圈散点分布在与向量OB相平行的直线上，当只有B点的方位角测量误差存在时，圆圈散点分布在与向量O′B相平行的直线上，当A和B2点的方位角测量误差皆存在时，圆圈散点分布在一个2-D区域内。该仿真实验证明了以上结论的正确性。

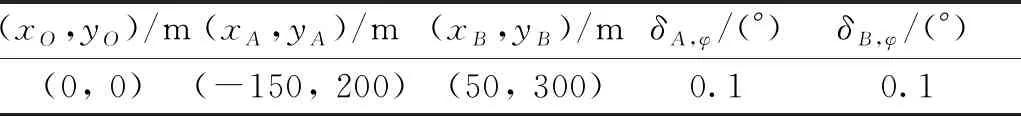
表2 DOA法的实验参数

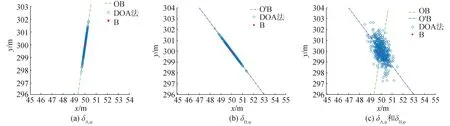
图6 DOA法的实验结果

接下来分析2种特殊情况：

1) 当ρAδA,φ=ρBδB,φ=λφ时，θ的取值等于(θA+θB)/2，ρAδA,φ近似反映了A点的方位角测量偏差在A点与OA相垂直的方向上所对应的距离偏差，ρBδB,φ近似反映了B点的方位角测量偏差在B点与OB相垂直的方向上所对应的距离偏差，也就是说当这2个距离偏差相等时，图5中的实线箭头恰好位于另外2个箭头中间，此时GDOA表达式为：

2.3 TOA-DOA法的误差分析

本小节对TOA-DOA法的协方差矩阵进行分析，将式(12)代入1.3节的MTD和NTD的表达式中可得:

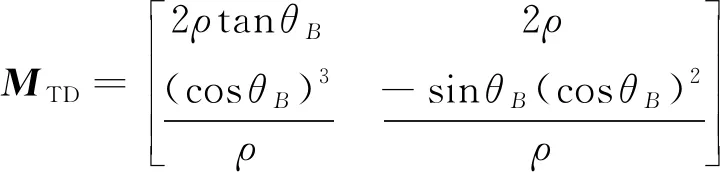
可以看出当B点与声信标不重合时，MTD是可逆的，即系统是可观测的。将MTD和NTD代入式1.3节GTD的表达式，则TOA-DOA法的导航误差的协方差矩阵的表达式可写为：

(18)

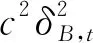
图7 TOA-DOA法的置信椭圆

为了对以上结论进行验证，本小节给出了如下的仿真实验，实验参数如表3所示，蒙特卡洛次数为500次。实验结果如图8所示，实心圆点是B点的真实位置，图中圆圈散点代表用TOA-DOA法得到的导航结果，可以看出当只有B点的时延测量误差存在时，圆圈散点分布在与向量OB相平行的直线上；当只有B点的方位角测量误差存在时，圆圈散点分布在与向量OB相垂直的直线上；当2种测量误差皆存在时，圆圈散点分布在一个2-D区域内。该仿真实验证明了以上结论的正确性。

图8 TOA-DOA的实验结果

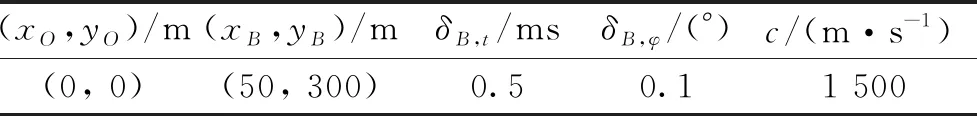
表3 TOA-DOA法的实验参数

3 3种导航算法置信区间的比较

第2节基于协方差矩阵对3种导航算法的导航误差进行了分析，在此基础上，本节对3种导航算法的导航误差的整体分布情况进行了比较。本节从2个方面对导航误差进行了比较：1)利用水平位置精度因子比较了3种导航方法的导航精度；2)比较了TOA法和DOA法的置信椭圆的形状。

3.1 水平位置精度因子

水平位置精度因子ε的本质是导航结果的均方根误差，其表达式为：

(19)

若定义G为导航误差的协方差矩阵，则ε可通过式(20)计算:

(20)

式中tr(*)表示取矩阵的迹。将第2节推导得到的GTOA、GDOA和GTD的表达式代入式(20)，其结果为：

(21)

(22)

(23)

若cδA,t≈cδB,t≈ρAδA,φ≈ρBδB,φ=λ，则(21)～(23)可化简为：

(24)

(25)

式中cδA,t(或cδB,t)表示A点(或B点)的时延测量偏差在A点(或B点)平行于OA(或OB)的方向上所对应的距离偏差，ρAδA,φ(或ρBδB,φ)近似反映了A点(或B点)的方位角测量偏差在A点(或B点)垂直于OA(或OB)的方向上所对应的距离偏差，式(24)和(25)说明了在以上几个距离偏差的测量精度相近的情况下，TOA法和DOA法的导航精度相近，并且在大部分情况下TOA-DOA法的导航精度高于TOA法和DOA法，当∠AOB的大小趋近于直角(|sin(θA-θB)|≈1)时，3种方法的导航精度相近。从式(21)、(22)和(24)也可以看出对于TOA法和DOA法，导航点A和B的选取满足夹角∠AOB近似为直角时，导航精度高。

3.2 置信椭圆

本节从置信椭圆的角度比较了TOA法和DOA法的导航误差。在这里定义了2种变量来描述这2种方法的置信椭圆，1)2个置信椭圆长轴的夹角，即2个协方差矩阵各自较大的特征值所对应的特征向量的夹角，定义为α；2)2个置信椭圆各自的长半轴和短半轴之比，分别定义为ηTOA和ηDOA，二者的数值越大，说明置信椭圆越狭长，由1.4节可知，ηTOA等于GTOA的特征值中的较大值与较小值之比的1/2次方，ηDOA等于GDOA的特征值中的较大值和较小值之比的1/2次方。

从第2节GTOA和GDOA的表达式可以看出，只有θA和θB以及各测量误差的方差会影响α、ηTOA和ηDOA的大小，为了便于分析，此处设δA,t=δB,t和δA,φ=δB,φ，图9(a)给出了当θA和θB取不同的值时α的大小。图中颜色越浅代表α的数值大小越趋近于90°。其数值统计结果如式(26)，

(26)

可以看出在大部分情况下，α的取值在70°以上，这也意味着在大部分情况下2种导航方法的置信椭圆的长轴趋近于垂直相交。

图9(b)给出了在θA和θB取不同值时ηTOA的计算结果，图9(c)给出了在θA和θB取不同值时ηDOA的计算结果，图中颜色越浅代表相应的数值越大。本文对计算结果进行了数值统计，其结果如下：

(27)

从图9的统计结果可以看出ηTOA和ηDOA在θA和θB取不同值时的整体分布情况相近，且在大部分情况下ηTOA和ηDOA的数值大小皆在2以上。通过以上的分析可以看出，在大部分情况下TOA法和DOA法的置信区间的形状较为狭长且二者趋近于垂直相交，二者的导航结果具有良好的互补特性。

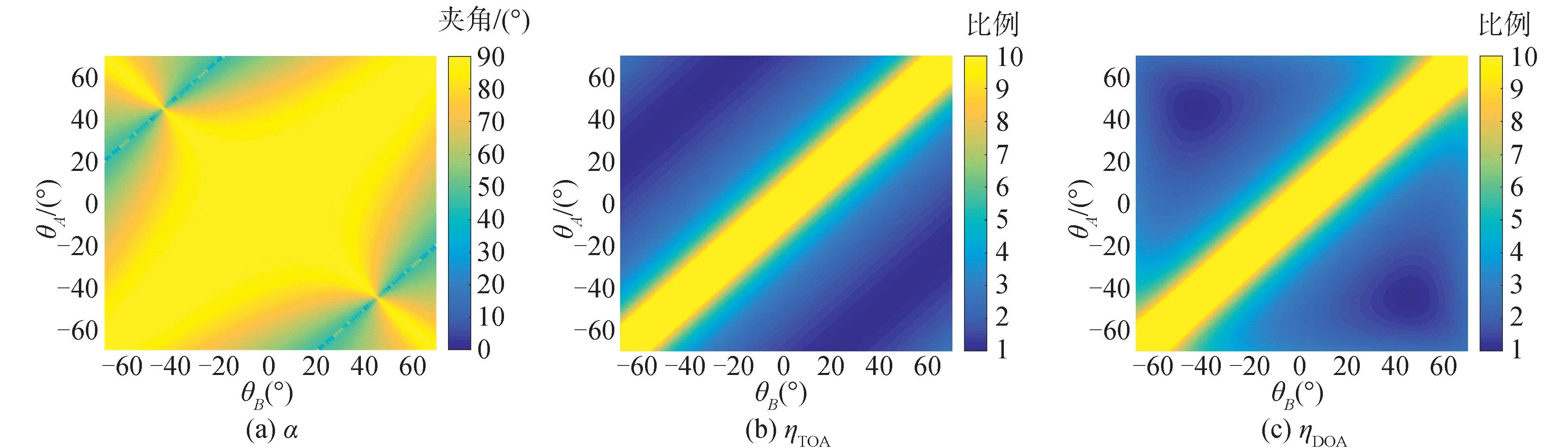
图9 θA和θB取不同的值时α、ηTOA和ηDOA的计算结果

3.3 仿真验证

本小节通过仿真对上述结论进行验证。本仿真考虑了6个场景，包含了∠AOB分别为锐角、直角和钝角的情况，前3种场景是在时延测量误差和方位角测量误差所对应的距离偏差近似相等的情况下进行的，后3种场景是在二者的距离偏差比例近似为1∶2的情况下进行的。相应的仿真参数如表4所示。此外A、B2点与声信标O点的距离为300 m，时延测量误差为0.5 ms，声速为1 500 m/s。

表4 不同场景下的实验参数

对于每种情况，同时给出了置信椭圆的计算结果(图10)和500次的蒙特卡洛实验结果(图11)。

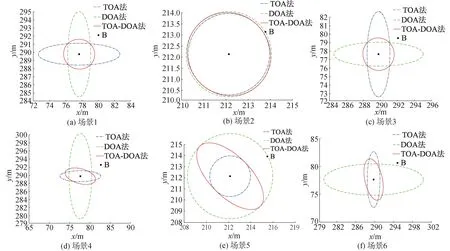
图10 6种场景的置信椭圆

图11 6种场景的蒙特卡洛仿真实验结果

从前3种场景的仿真结果可以看出：当∠AOB为锐角和钝角时，TOA法和DOA法导航结果的置信区间大于TOA-DOA法的置信区间，当∠AOB为直角时，3种方法的导航结果的置信区间近似一致，这与3.1节的结论相一致，即当时延测量误差和方位角测量误差所对应的距离偏差的测量精度相近时，TOA-DOA法的导航精度在大部分情况下高于TOA法和DOA法，且当∠AOB的大小趋近于直角时，3种方法的导航精度相近；此外，当∠AOB为锐角和钝角的情况时，TOA法和DOA法导航结果的置信区间皆较为狭长且近似垂直相交，这证明了3.2节结论的正确性。

对比前后3个场景的仿真结果可以看出：当方位角测量误差增大了1倍时，DOA法置信椭圆的长轴和短轴皆增大了1倍，置信区间面积增大了3倍；TOA-DOA法置信椭圆在B点和声信标连线的垂直方向的半轴增大了1倍，相应地置信区间面积增大了1倍；在时延测量误差和方位角测量误差所对应的距离偏差不对等的条件下，TOA-DOA法不能保证比TOA法和DOA法获得更高的导航精度。