带片体的滑行艇高速航行纵稳性研究

2022-02-16王建东庄佳园毕效笙罗靖苏玉民

哈尔滨工程大学学报 2022年1期

王建东，庄佳园，毕效笙，罗靖，苏玉民

(哈尔滨工程大学水下机器人重点实验室，黑龙江哈尔滨 150001)

滑行艇因其棱柱式构型，具有较高的快速性，被广泛应用于海岸巡逻、环境监测等领域[1]。但其高速高机动航行时，因纵向失稳常出现海豚运动、砰击与失速等现象，严重情况下甚至发生倾覆。因此，为提升其最大航速，同时保证无人艇上设备的正常使用，高速航行阶段需其具有更好的动稳性，这是至今船舶总体技术和流体力学领域没有得到很好解决的问题[2]。

有关滑行艇的水动力试验的研究最早出现在Chambliss等[3]撰写的有关棱柱型滑行面的水动力试验研究报告；但其纵稳性的研究却源于Clement等[4]对TMB62滑行艇开展的一系列静水阻力试验，试验中观测到了海豚运动现象，并测量了海豚运动发生的临界速度；Wellicome等[5]对滑行艇的横向力及力矩进行了测量，讨论了重心高度和斜升角对艇横向稳定性的影响；Blount等[6]应用试验方法，对滑行艇非线性振动不稳定性问题进行了研究，并通过试验数据给出了艇发生动横倾的判定条件；Katayama等[7]对航速超过100 kn的滑行艇失稳现象进行了试验研究，结合纵倾角和艉部吃水对横稳性损失发生的界限进行了判定，并讨论了极高航速下带有横倾角或艏摇角情况下的航行受力情况。

国内关于滑行艇稳性性能的试验和数值研究则较少。凌宏杰等[8]基于Fluent软件编制了耦合求解滑行艇纵向运动响应的预报程序，分析了航速和重心纵向位置对海豚运动中运动响应的影响；孙寒冰等[9]针对无人艇航行时的纵向稳定性问题，基于拖曳试验和动网格技术，发现重心位置的前移有利于避免海豚运动的发生；王硕等[10]开展了滑行艇高速滑行阶段横稳性损失试验和数值研究，得到不同横倾角下艇的横稳性损失与航速、质心纵向位置和航行纵倾角间的关系；倪阳[11]建立了考虑流动分离的有限楔形体入水砰击的半解析理论模型，并基于2D+T理论对滑行艇高速航行时纵向不稳定运动进行了预报；李亚军[12]通过线性稳定分析和非线性2D+T理论数值预报了海豚运动的发生，探讨了艇的重心位置、排水量、斜升角等重要参数对海豚运动的影响；姜正桥等[13]利用周期变推力方法对滑行艇海豚运动的控制进行了仿真，证明了在不失速前提下，周期变推力控制能够准确跟踪并有效抑制滑行艇的海豚运动。

由于试验的繁琐和较高的计算代价，加之喷溅、射流等非线性因素干扰，国内外目前关于滑行艇高速航行时纵稳性方面的研究较少。本文开展了带片体的滑行艇高速航行时纵稳性数值研究，进行了单体艇的静水拖曳试验，利用全因子设计空间采样法和重叠网格技术对三体艇高速航行发生海豚运动时的纵向运动响应和水动力特性进行计算，分析了片体纵垂向位置对艇高速航行时纵稳性的影响，优选出具备较好纵稳性能的纵垂向片体位置。

1 模型试验

1.1 模型简介

选取非断级式含有多个防溅条的细长型方艉单体滑行艇作为主船体，与横断面瘦尖、整体细长且舭部竖直的片体经支架连接组成三体滑行艇。单体与三体滑行艇的模型及主尺寸分别如图1和表1所示，更多的艇型细节见文献[14]。

图2 主船体和片体的型线

表1 单体艇与三体艇母船型的主尺度

1.2 静水拖曳试验

模型的静水拖曳试验在中国特种飞行器研究所高速水动力实验室进行，仅针对单体艇进行静水拖曳，共计完成4个工况，如表2(τ0为初始纵倾角)所示。试验装置安装及试验结果可参阅文献[14]，获得Fr=1.26时单体艇的试验场景如图3所示。

表2 拖曳试验工况

图3 Fr=1.26时单体艇的试验场景

2 数值计算方法及有效性验证

2.1 计算方法

根据试验内容，采用基于有限体积法的Star-CCM软件对单体艇试验工况2，各航速下船体周围的绕流场进行求解，引入SSTk-ω湍流模型[15]，根据力和力矩的平衡求得艇体所受到的力和力矩，之后对模型六自由度运动求解，并进行速度和角速度积分获得艇体的位移和角位移。

2.2 计算域和网格划分

考虑流动对称性，仅建立半侧艇计算域，背景域和重叠域分别采用切割体和棱柱层网格划分，船体周围采用边界层并进行适当的水线面加密，无量纲化近壁面网格高度y+[16]。

(1)

式中:y是边界层中第1层网格节点到近壁面的高度；U是航速；L是滑行艇水线长度；υ是流体粘度系数；通常计算中，30≤y+≤300，这里y+=250。

利用重叠网格技术模拟滑行艇在计算域中的运动，计算域范围、边界条件和网格划分分别如图4和图5所示。

图4 计算域的范围和边界条件

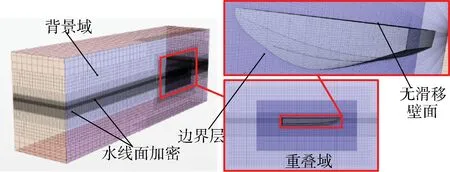
图5 计算域的网格划分

另外，综合考虑计算精度和运行时间，确定时间步长Δt=0.006 s，最大内部迭代设置为5，总计算时间设置为20 s。

2.3 有效性验证

基于上述模拟设置，选取Fr=1.26速度点，依次从网格尺寸参数、y+和时间步长Δt三方面对数值计算的收敛性进行检验。计算完成后，综合考量计算精度和计算时间，选取文献[16]中网格2的尺寸参数、y+=250和Δt=0.004 s作为模拟的基础设置。并基于此，计算后得到单体艇试验工况2、各航速下的总阻力RT、升沉hm和纵倾角θm的试验值(EFD)和模拟值(CFD)的对比如图6，误差如表3所示。

由图6可见，随着航速增加，单体艇的RT、hm和θm的模拟值和试验值变化趋势均一致，但数值计算得到的RT同试验值相比，误差随航速的增加变得越来越大。这主要是因为在高速滑行阶段，喷溅阻力占总阻力比例较大，计算的网格大小对于喷溅、射流等非线性因素无法作出有效地捕捉，然而此时对于hm和θm则能作出准确的模拟。

图6 总阻力、升沉和纵倾角的试验值和模拟值对比

另外，由表3可知，在滑行阶段(Fr>1.05)，数值计算得到的RT、hm和θm同试验相比最大误差分别为-18.15%、7.85%、-6.19%，均出现在Fr=2.52处，这表明本文采用的数值计算方法对滑行艇滑行阶段，航行姿态的预报具备一定的计算精度，但对高速滑行阶段(Fr>2.1)总阻力的预报稍弱。

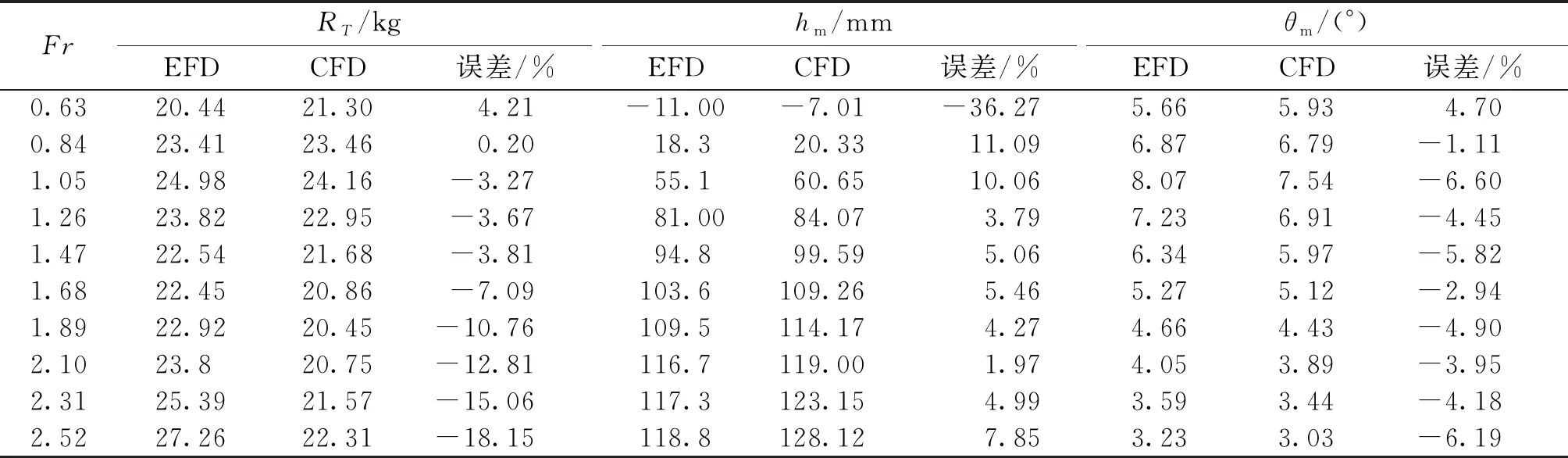
表3 单体艇的总阻力、升沉和纵倾角的试验值和模拟值的对比

3 计算结果及分析

3.1 三体艇海豚运动中的响应

滑行艇的海豚运动现象，即当艇的航行姿态和航速达到一定条件时，出现周期性的纵摇和升沉耦合振荡现象。本文将是否发生海豚运动，以及发生海豚运动时艇的垂荡和纵揺运动响应作为评价滑行艇高速航行时纵稳性优劣的评价指标。

依次对单体和三体艇10≤v≤13 m/s时，Δ=137.3 kg、LCG=882 mm(工况5)和Δ=137.3 kg、LCG=830 mm(工况6)2种工况下的静水直航进行模拟，计算稳定后得到v=13 m/s时单体艇和三体艇的波面情况如图7所示，从图7中可清晰地观察到高速航行发生海豚运动时艇艉的空穴和尾流。之后将单体和三体艇是否发生海豚运动的结果汇总，具体如表3。表4中，“+”表示发生海豚运动，“0”表示发生海豚运动的临界状态或计算稳定后垂荡和纵揺出现微小的波动，“-”表示未发生海豚运动。

图7 v=13 m/s时单体艇和三体艇的波面情况

表4 不同航速单体艇和三体艇发生海豚运动结果对比

由表4可知，工况6下，v=13 m/s时，单体艇和三体艇都发生了海豚运动，而在v=12 m/s时，相比单体艇，三体艇仅出现了微小的垂荡和纵揺波动，v=11 m/s时三体艇的海豚运动现象已消失。工况5下，v=13 m/s时三体艇也仅出现了微小的垂荡和纵揺波动，10≤v≤12时，三体艇的海豚运动均已消失，2种工况的模拟结果均表明增设片体可以一定程度上延缓滑行艇海豚运动发生，提高滑行艇的最大航速和纵向稳定性。

进一步得到工况6下发生海豚运动时，前10 s内两艇的垂荡h和纵揺θ运动响应如图10所示。由图可知，三体艇在10≤v≤13各航速时垂荡和纵揺的运动响应相比单体艇均要小得多，在v=10 m/s或11 m/s时三体艇甚至并未出现海豚运动，这进一步证明了增设片体可以一定程度上提高滑行艇高速航行时的纵稳性。

3.2 片体布置对滑行艇高速航行纵稳性的影响

3.2.1 片体纵垂向位置调整

为进一步分析片体纵垂向位置对三体艇高速航行纵稳性的影响，改变片体相对主船体艉封板距离a值，并维持片体横向位置b=0.548 m不变，获得片体纵向a=0.1Lm、0.2Lm(重心处)、0.3Lm、0.4Lm和0.5Lm5种不同位置，调整方式具体如图12。

保证三体艇总排水量Δt不变，片体垂向位置调整方式如图13。图中实线和虚线分别代表调整的前后位置，c表示片体相对主船体基线距离，d表示水线位置，Δdh表示调整前后主船体基线位置的变化量。获得a=0.1Lm、b=0.548 m时，片体的4种不同垂向位置如表5所示，Sm和Sd分别代表主船体和片体的水线面积。

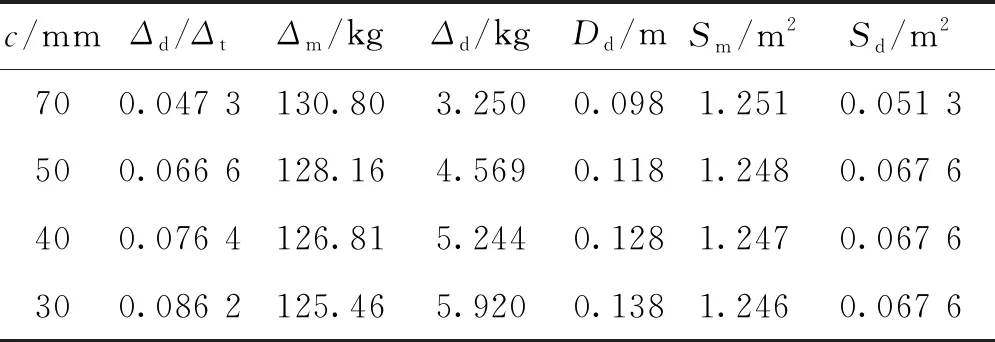
表5 片体的不同垂向位置

图8 v=10 m/s时单体艇和三体艇的纵向运动响应对比

图9 v=11 m/s时单体艇和三体艇的纵向运动响应对比

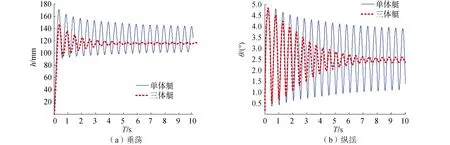
图10 v=12 m/s时单体艇和三体艇的纵向运动响应对比

图11 v=13 m/s时单体艇和三体艇的纵向运动响应对比

图12 片体纵向位置调整方式

图13 片体垂向位置调整方式

3.2.2 片体纵垂向位置优选

为延缓滑行艇高速航行时海豚运动的发生，提高其最大航速，利用全因子法对片体纵垂向位置设计空间进行采样，并采用相同的模拟设置对上述样本点进行计算，获得工况6下，v=12,13 m/s时片体纵垂向位置对三体艇是否发生海豚运动的影响结果分别如表6和表7，进一步地，获得v=12,13 m/s时，片体不同纵垂向位置所对应的三体艇垂荡ha和纵揺幅值θa分别如图14和15所示。

表6 v=13 m/s时片体纵垂向位置对滑行艇海豚运动的影响

表7 v=12 m/s时片体纵垂向位置对滑行艇海豚运动的影响

由表6和7可知，0.1≤a≤0.3Lm,30≤c≤70时，三体艇高速航行时仅出现微小波动的运动响应，c=30， 40 mm，a=0.1Lm，0.2Lm时甚至并未出现海豚运动，这说明片体垂向上增加浸深，纵向上位于重心附近或适当靠后，可有效地延缓单体艇海豚运动的发生，提高其高速航向时纵稳性。另外，从图14和15看出，片体纵向越靠近艇艏，发生海豚运动时垂荡和纵揺的运动响应越大。

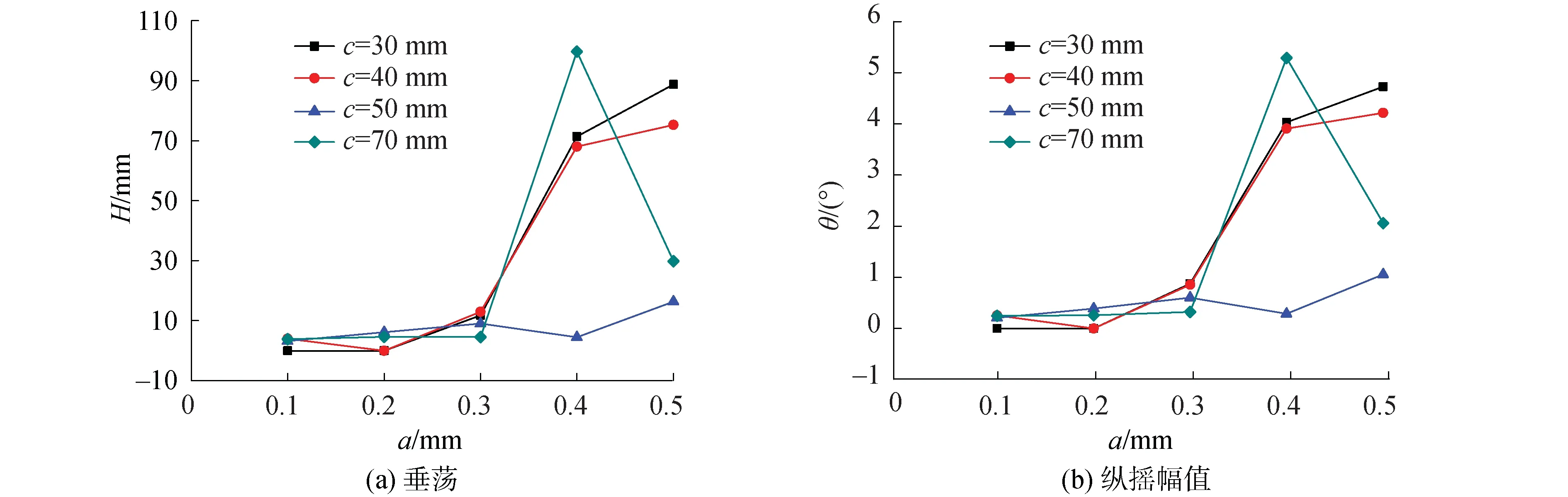
图14 v=13 m/s时工况6下三体艇的垂荡和纵揺幅值

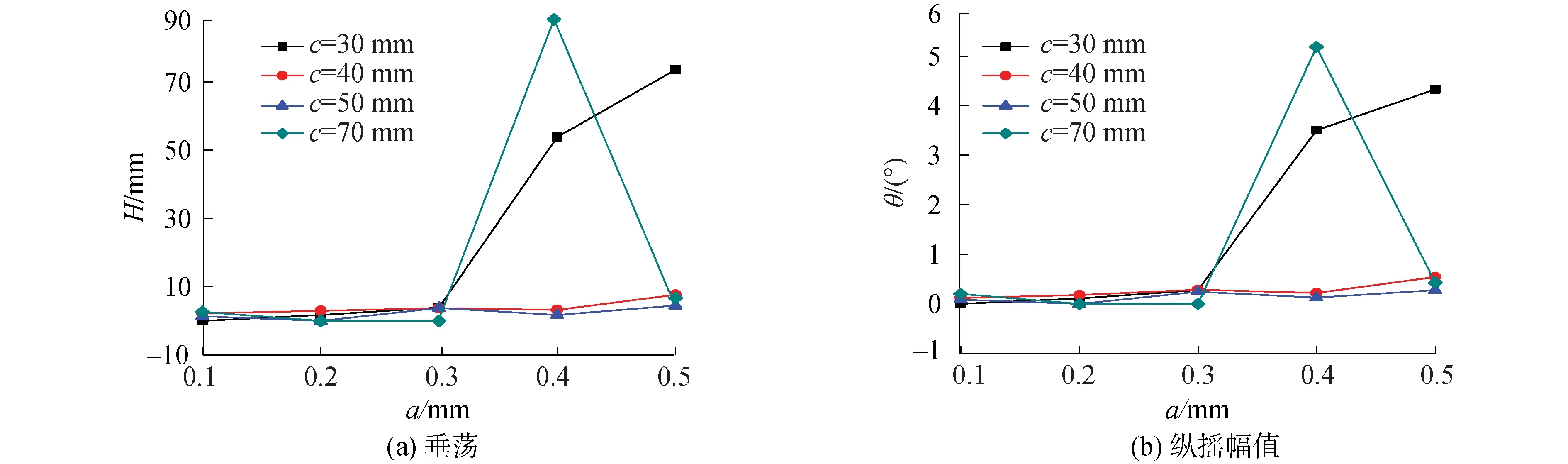
图15 v=12 m/s时工况6下三体艇的垂荡和纵揺幅值

相比之下，优选出具有较好纵稳性能的片体纵垂向位置a=0.2Lm，c=30 mm，获得其与单体艇v=13 m/s时垂荡和纵揺的运动响应对比结果如图16所示；进一步地，获得此时单体和三体艇周围，绕流场情况的速度卷积和流线对比结果分别如图17和图18所示，由图观察知，片体周围速度较小，根据伯努利方程，片体此时会受到一定大小的动升力；改变片体垂向、纵向位置相当于调整片体所受到的升力大小和水动压力作用点，当主船体和片体的总浮力、流体动升力等于重力，绕重心的纵向力矩达到平衡，即实现了海豚运动的抑制。