水下航行器艇体形状对阻力及流噪声综合影响
2022-02-16姜宜辰赵月熊济时杨雨浓张桂勇
姜宜辰, 赵月, 熊济时, 杨雨浓, 张桂勇
(1.大连理工大学 船舶工程学院,辽宁 大连 116024; 2.高新船舶与深海开发装备协同创新中心, 上海 200240; 3.中国船舶及海洋工程设计研究院, 上海 200011; 4.中国舰船研究设计中心,湖北 武汉 430064)
近年来水下航行器在在民用和军用方面快速发展,在地形测绘、资源勘测、水下侦查、水下攻击等方面发挥着越来越重要的作用[1-2]。水下航行器执行任务时,其快速性和隐身性是非常重要的性能指标。
阻力是影响航行器快速性的重要因素,近年来很多学者对水下航行器外形与阻力的关系进行了系统性的研究。Meng等[3]采用经验公式和CFD方法对4种不同头部形状航行器的阻力进行了计算,最终得到了阻力小且空间大的艇型。庞永杰等[4]进行了Myring型回转体直航阻力实验和数值计算研究,采用多岛遗传算法对回转体参数进行全局寻优,得到了一组阻力最优的艇型。戴鹏[5]基于Myring方程进行了水下航行器的总体设计工作,以阻力、螺旋桨效率等性能参数为目标,对航行体的外形进行了参数优化,最终得到了快速性、稳性和经济性均较优的水下航行器。ZHENG[6]利用自动化计算平台对不同参数的Myring型回转体阻力进行了计算,得到了适用于不同航速的艇体阻力快速估算模型,并应用模型得到了阻力较小的艇体形状。
水下航行器的辐射噪声量级决定了航行器的隐身性,流噪声是除机械噪声、螺旋桨噪声外的第3大噪声源。降低流噪声不仅能有效降低水下辐射噪声,对降低艇体自噪声,提高声呐设备的探测能力具有重要意义[7]。潘光等[8]应用大涡模拟和FW-H方程对AUV运载段凸台形状对阻力和流噪声的影响进行了研究,探究了不同凸台截面形状和尺寸的减阻降噪规律。张磊等[9]应用大涡模拟结合ACTRAN声学软件对2种头部线型回转体的流噪声进行计算。结果表明在速度、攻角相同的情况下,头部端面半径小、头部长度较长的模型具有较好的流噪声性能。
目前已有研究重点关注航行器头部形状对阻力或流噪声的影响,而对艇体其他部位形状对流噪声大小的影响规律缺乏系统全面的认识。且目前已有研究大多单一分析艇体形状对快速性和隐身性的影响,缺乏艇体形状对快速性和隐身性的综合影响规律揭示,而在航行器总体设计时艇体形状需兼顾快速性和隐身性。为综合研究艇体形状对水下航行器快速性和隐身性的影响,本文通过参数化数学模型Myring方程控制AUV形状,应用CFD方法和FW-H方程计算不同艇体形状的回转航行器的阻力以及流噪声水平,分析不同形状艇体的阻力及流噪声规律,得到阻力小和流噪声水平低的艇型,从而为水下航行器的总体形状设计提供参考。
1 数学模型
1.1 Myring方程
使用Myring方程来确定AUV的形状。Myring方程是常用的回转水下航行体艇型控制方程,广泛使用于艇的形状设计以及快速性研究等[4,10-11]。方程形式为[12]:
r1(x)=0.5D[1-((x-a)/a)2]1/n
(1)
r2(x)=0.5D-[(3D)/(2c2)-tgθ/c]+[D/c3-tgθ/c2](x-a-b)3
(2)
方程(1)控制回转体的头部形状,方程(2)控制尾部形状,中间由平行中体连接。Myring方程参数示意图如图1所示。参数a为头部长度,b为平行中体长度,c为尾部长度,D为艇直径,n为控制头部形状的系数,n越大头部越饱满,θ为控制尾部形状的系数,数值上等于尾端形状的切线与中心线的夹角,θ越大尾部越饱满。

图1 Myring方程几何参数参数示意
本文选取艇几何参数如表1所示,包括7个艇体形状。所有艇长度L为3 200 mm,直径D为400 mm,长宽比为8。编号n1、n2、n4这3个艇系数n不同,拥有不同的头部形状。编号θ5、θ15、θ25三艇系数θ不同,拥有不同尾部形状。编号a200、a600、a1450三艇参数a、b、c的值不同,拥有不同的平行中体长度。7个艇体分成3个系列,分别探究头部形状、尾部形状和平行中体长度对阻力和流噪声水平的影响。不同艇体形状如图2所示。
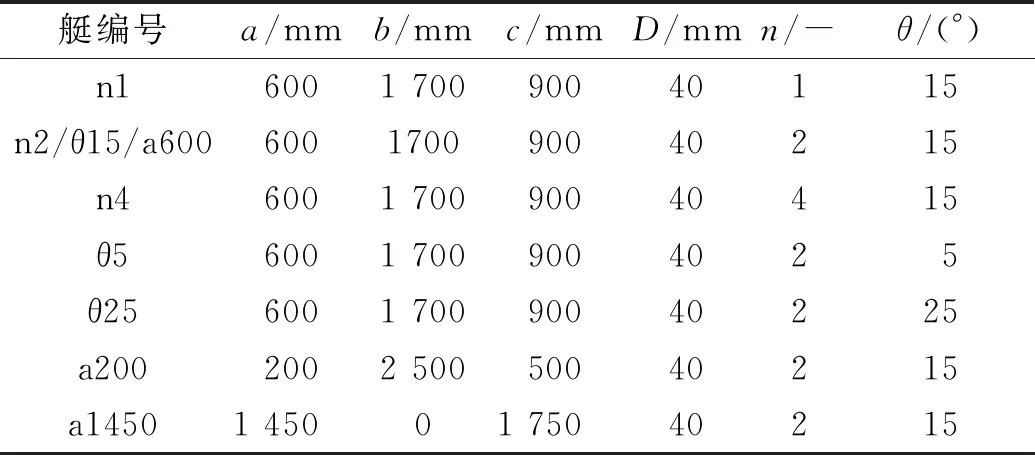
表1 不同艇体几何形状参数设置

图2 不同艇体几何形状对比
1.2 流场求解方程
水下航行体周围流动的控制方程包括连续性方程和动量方程:
(3)
(4)
式中:i和j分别为变量在坐标系中第i方向及第j方向的分量;P为压力;u为速度矢量;ρ为流体密度;f为质量力。
1.3 FW-H方程
FW-H方程是为解决自由运动物体在流体中的发声问题提出的,方程形式为[13]:
(5)
Pij为压应力张量:
(6)
式中:i和j分别为变量在坐标系中第i方向及第j方向的分量;p为远场声压;f为与壁面距离有关的函数;δ(f)为狄拉克函数;δij为克罗内克δ函数;Tij为莱特希尔应力张量;ui和un分别为速度在i和n方向上的分量;a0为远场声速。
2 计算方法及准确性验证
2.1 计算设置
使用STARCCM+13.02软件进行阻力及流噪声的计算。阻力部分使用Realizablek-ε两层模型[14]进行稳态定常计算,迭代步数2 000步;流噪声部分应用定常计算的结果为初始条件,使用LES湍流模型[15]和FW-H方程进行非定常求解,内部迭代为5步,时间步为0.000 1 s,在流场稳定的基础之上计算0.5 s,雷诺数为1.2×107。
计算域和边界条件如图3所示。为减小边界对计算结果的影响,计算域边界距艇体有足够的长度。计算域速度进口在艇前1倍艇长处,压力出口在艇后2倍艇长处,四周设置为对称平面距艇中心5倍艇直径。使用切割体网格进行空间离散,切割体网格具有曲面捕捉准确,计算效率高,稳定性好等优点。在边界层附近等流动复杂区域进行网格加密,以解析艇体周围复杂的流动。在离艇较远位置处网格较大,可以节约一定的计算资源,第1层网格法向厚度满足y+<1,匹配湍流模型对近壁面附近流动求解的要求。中纵剖面网格的网格如图4所示。

图3 流域划分以及边界条件设置

图4 中纵剖面网格划分
2.2 计算准确性验证
通过计算有详细实验数据的SUBOFF模型[16],并与实验数据对比以验证数值模型的准确性。SU-BBOF几何形状如图5所示,艇长4.356 m,艇身最宽处为0.508 m。计算来流速度为3.05 m/s,雷诺数为1.2×107。

图5 SUBOFF几何模型
改变网格基础尺寸,划分了171万、268万、411万、656万4种不同数量的网格进行网格无关性验证,不同网格的总阻力计算结果如表2所示。
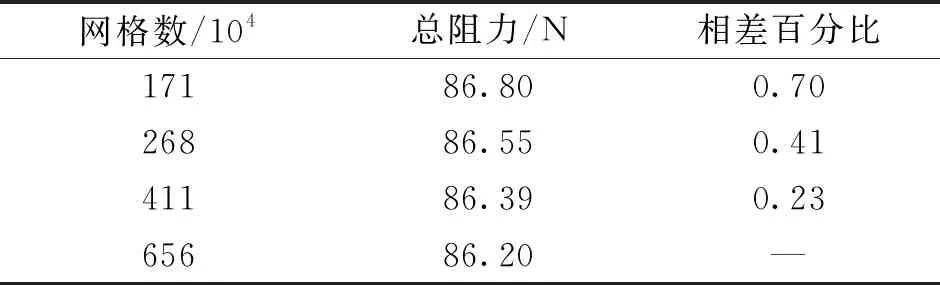
表2 网格无关性验证
阻力相差百分比定义为(T-Tm)/Tm,T为该网格数阻力计算值,Tm为最大网格数阻力计算值。当网格数增加至411万时阻力计算结果和656万网格仅相差0.23%,可以认为计算结果已趋于收敛,后续计算均采用411万网格时的础尺寸以及加密形式。
图6和图7为艇表面压力系数以及壁面剪切力系数计算值与实验值的对比,压力系数计算值和实验值最大偏差为0.035,剪切力系数计算值和实验值的最大偏差为0.000 47。可以证明计算值和实验值有较好的一致性,验证了阻力计算的准确性。
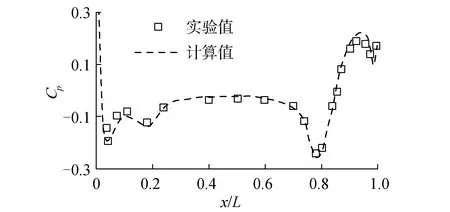
图6 压力系数验证

图7 剪切力系数验证
目前公开发表的有关水下航行器流噪声的实验数据较少,且存在水下环境背景噪声难以消除的问题,本文采用对比李玲等在北京航空航天大学的D5气动声学消声风洞进行的圆柱绕流气动声学测量实验[17]的实验数据来验证流噪声计算方法的准确性。流域划分及边界条件设置如图8所示。实验测量了直径为0.02 m的圆柱在不同流速下的噪声,监测点在距离圆柱轴线2 m并与流速方向垂直的位置。
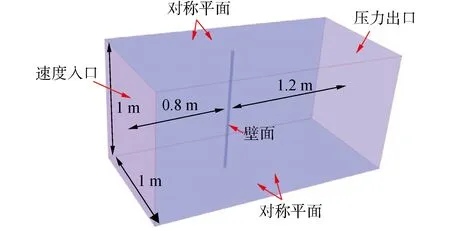
图8 圆柱绕流流域划分及边界条件设置
监测点的流噪声数值和实验结果的对比如图9和图10所示。50 m/s速度下声压级峰值频率计算值和实验值相差46 Hz,声压级计算值比实验值偏小6.58 dB;60 m/s速度下声压级峰值频率计算值和实验值相差69 Hz,声压级峰值计算值比实验值偏小6.94 dB。从数值和实验结果的对比来看,峰值频率处的声压级大小存在一定偏差,但从整个频率范围来看计算值与实验值的趋势显示出较好的一致性,验证了流噪声计算的准确性。
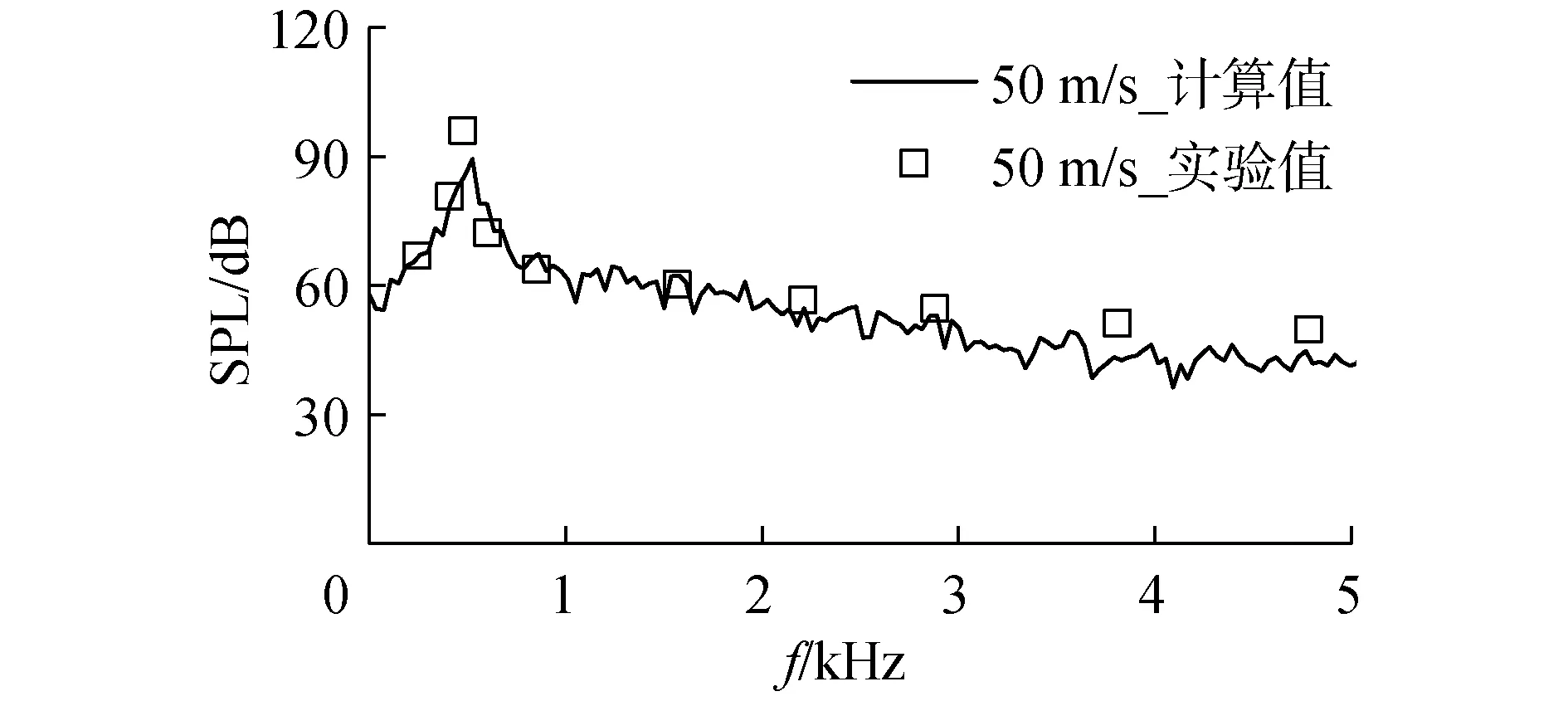
图9 50 m/s流速下圆柱流噪声结果验证

图10 60 m/s流速下圆柱流噪声结果验证
3 计算结果
3.1 流场计算结果
定义3种阻力系数公式为:
Ct=T/(0.5ρv2s)
(7)
Cf=F/(0.5ρv2s)
(8)
Cr=R/(0.5ρv2s)
(9)
式中:T、F、R分别为总阻力、摩擦阻力和压差阻力;ρ为水的密度;v为无限远处来流速度;s为艇体表面积。
阻力系数的计算结果如表3所示(为方便对比,表中数值均为阻力系数放大1 000倍结果)。从n1、n2、n4的阻力计算结果来看,头部越丰满,摩擦阻力系数越小,压差阻力系数越大。三者中总阻力系数最小为头部中等饱满的n2艇。θ5、θ15、θ25三艇阻力系数结果显示,尾端夹角越大,摩擦阻力系数越小,压差阻力系数越小。三艇中阻力系数最小的艇为尾部外凸的θ25。从a200、a600、a1450三艇的阻力系数结果来看,随着平行中体长度的减小,总阻力系数减小,并且这种减小主要是由于压差阻力系数减小导致的。
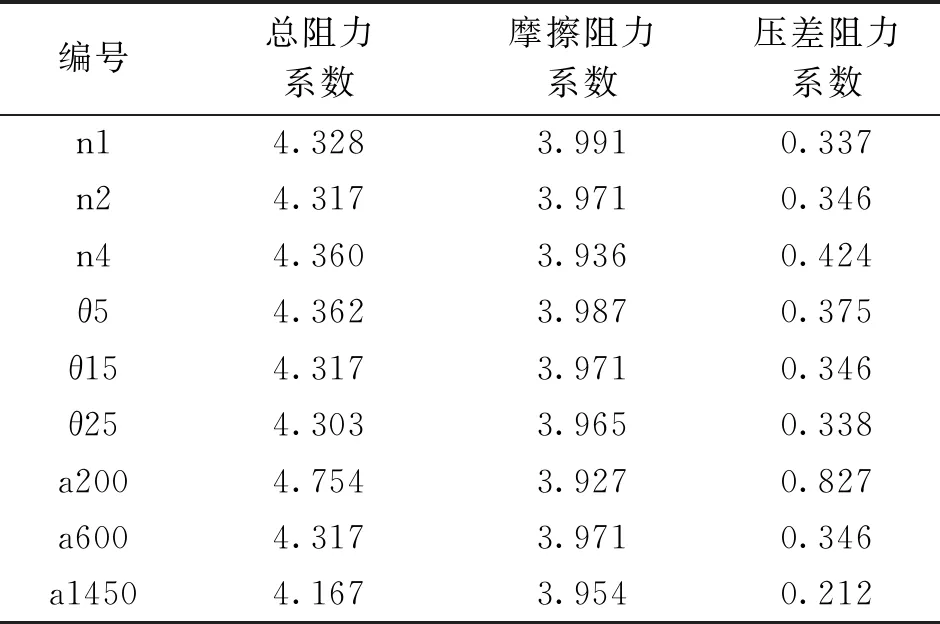
表3 不同艇阻力系数计算结果
定义艇表面压力系数和剪切力系数:
CP=P/(0.5ρv2)
(10)
Cτ=τ/(0.5ρv2)
(11)
式中:P为艇表面压力;τ为艇表面剪切力;ρ为水的密度;v为水的速度。压力系数及剪切力系数计算结果如图11所示。n1、n2、n4艇的压力系数结果显示,头部形状对前端压力的大小有非常明显的影响。头部丰满会使压力沿艇长方向更快地减小。从剪切力系数计算结果看,饱满头部会使头部剪切力增大,且使剪切力最大位置靠近前端。θ5、θ15、θ25艇的压力系数显示尾端夹角增大会使尾部压力系数拐点略微向后移动,拐点处压力减小,压力系数在尾部的变化更为平缓。不同尾部形状艇体的剪切力系数也呈现类似的规律,随着夹角度数增大,剪切力系数拐点略微向后移动,在尾部剪切力系数变化曲线更为平直。a200、a600、a1450三艇由于平行中体的长度变化很大,头部尾部形状均产生了较大变化,头部和尾部的压力系数及剪切力系数均有较大不同,可以看出平行中体长度越小,压力系数和剪切力系数的拐点越向中部靠拢,变化幅度越小。

图11 不同艇的压力系数、剪切力系数
不同艇速度场对比如图12、13所示。从速度场的变化可以一定程度上理解压力系数和剪切力系数的变化规律。n1、n2、n4艇的头部速度场显示,头部丰满则高速区前移和向前方扩大,对应着压力系数及剪切力系数拐点的提前。θ5、θ15、θ25艇的尾部速度场显示,尾端夹角越大则高速区小幅后移,且高速区域减小,尾部边界分离延缓,对应着压力系数及剪切力系数尾部拐点后移以及曲线变化更为平缓。
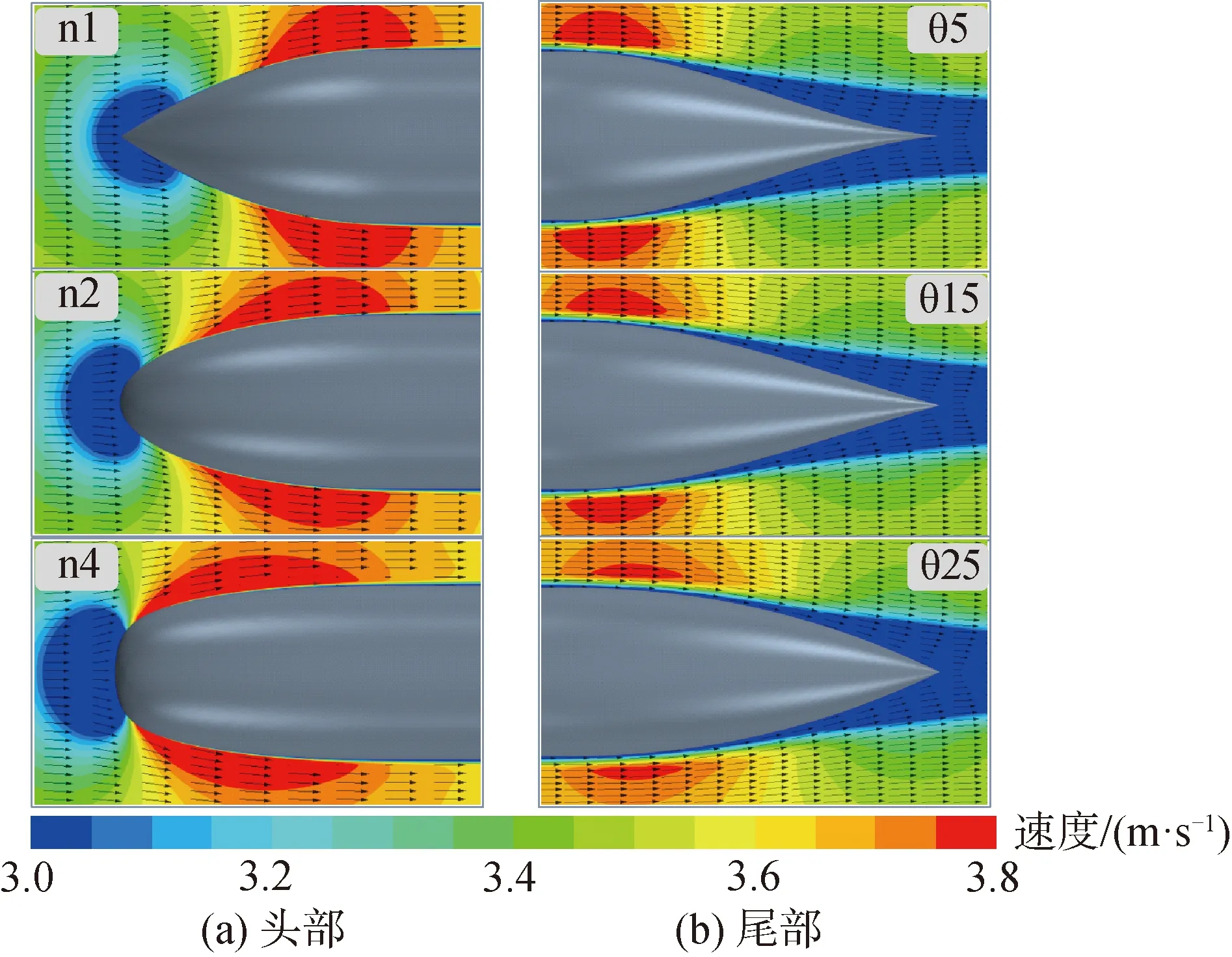
图12 不同形状艇体速度场对比

图13 不同平行中体长度艇体速度场对比
a200、a600、a1450三艇速度场显示,平行中体长度越小,高速区域向中间移动且高速区变小,a1450艇高速区甚至消失,对应着压力系数与剪切力系数的拐点的靠中与变化幅度的减小。
3.2 流噪声计算结果
以艇中心为圆心,20 m为半径,分别在中横中纵剖面上设置36个监测点(每10°一个),如图14所示。取ZH9/ZZ9位置为特征点(ZZ9和ZH9位置相同),来分析声压级频谱规律。
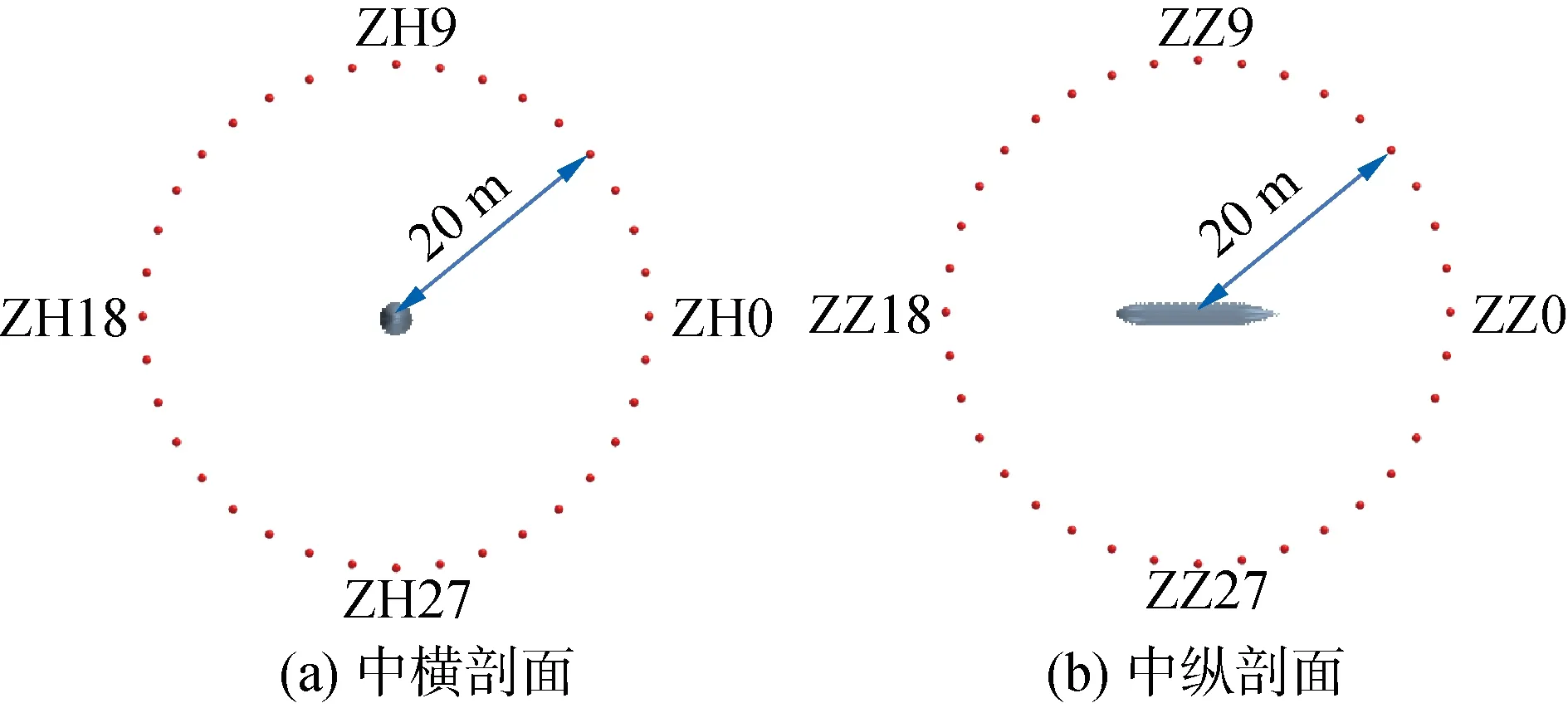
图14 中横剖面、中纵剖面监测点设置
特征点声压级频谱的计算结果如图15所示(本文所有声压级结果均为等效至1 m后结果,参考声压为1×10-6Pa),所有艇的声压级的峰值均出现在460~530 Hz范围。对比n1、n2、n4三艇特征点声压级频谱图,可知三艇在不同频率处声压级比较相近。对比θ5、θ15、θ25三艇频谱图,发现在3 000~5 000 Hz范围内声压级大小规律为θ5>θ25>θ15,说明回转体尾部形状改变会影响中高频流噪声的大小。从a200、a600、a1450三艇的频谱图可知三艇的声压级大小相差较大,规律为:a200>a600>a1450。

图15 不同艇在特征点(ZH9/ZZ9)处声压级频谱
总声压级综合了不同频率成分的声压级大小,可以代表整个频率范围内流噪声的大小。总声压级公式为[18]:
OSPL=10lg(100.1SPL1+100.1SPL2+…+100.1SPLn)
(12)
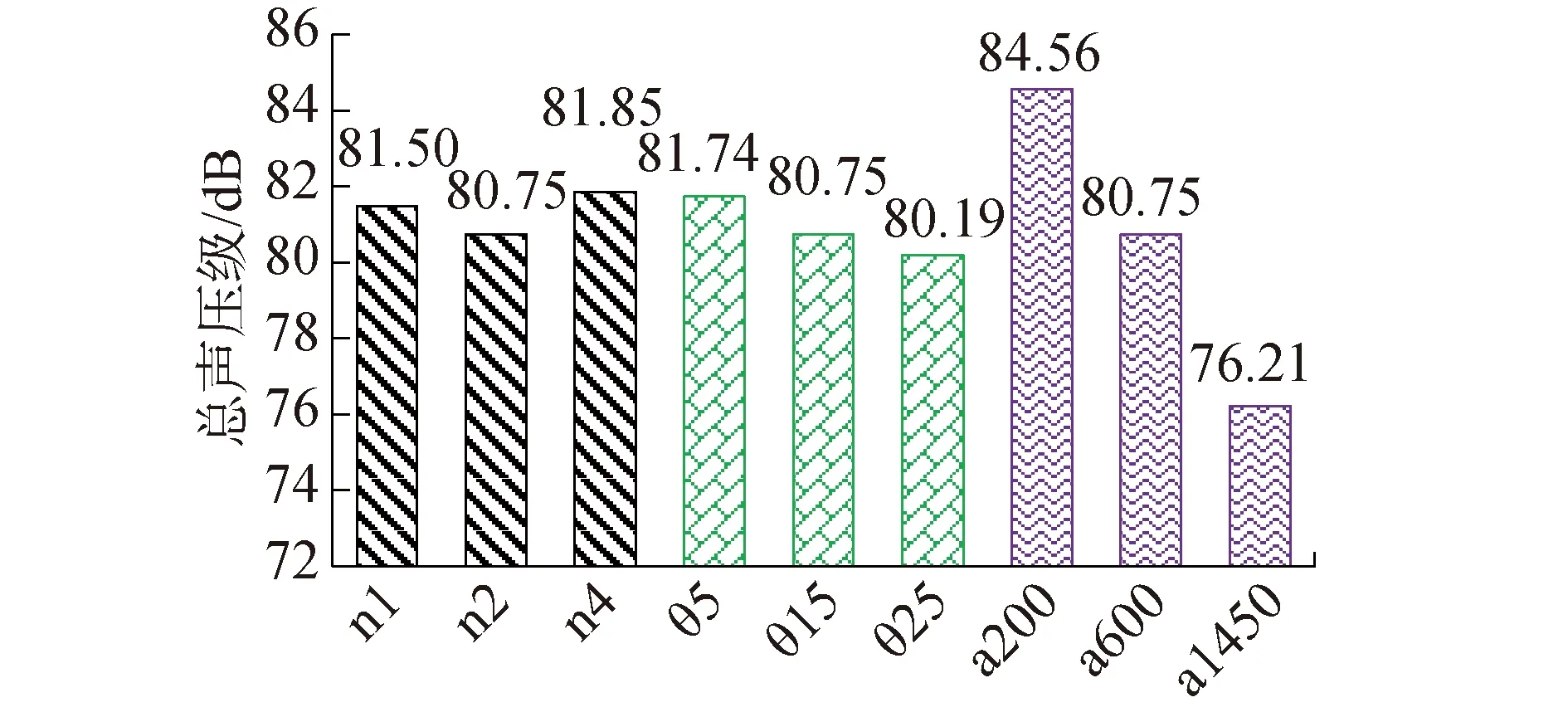
式中:SPL1、SPL2、…、SPLn为不同频率处声压级。根据总声压级计算公式计算了不同艇特征点处的总声压级,结果如表4所示,可以看到特征点纵声压级大小规律为n2 表4 单一特征点(ZH9/ZZ9)总声压级计算结果 计算中横中纵剖面上不同监测点的总声压级,得到了如图16所示的中横中纵剖面声压级指向性图,可以看出艇在中横剖面不同方向的声压级大小较为一致,指向性图呈圆形,而在中纵剖面的上下方向要比前后方向大8~15 dB,呈现类8字形的指向性结果。 图16 不同艇体形状声压级指向性 为了定量表示不同艇流噪声大小,叠加中横中纵剖面72个监测点的声能量并取平均值,计算了不同艇体总声压级,计算结果如图17所示。从图17的结果可以判断流噪声大小规律为n2 图17 不同艇总声压级计算结果 1)艇体头部为尖端形式或过于饱满对快速性和隐身性不利,头部中等饱满时阻力和流噪声较小。 2)内凹式艇尾的艇体阻力和流噪声都比较大,而外凸式艇尾的艇体阻力和流噪声比较小。 3)在保持艇长和艇宽不变的情况下,平行中体长度越小,阻力和流噪声越小,当没有平行中体时艇体呈现出水滴型潜艇型状,阻力值以及流噪声水平最低。 4)数值仿真结果验证了回转体艇体形状对阻力与流噪声的影响相一致的规律,阻力小的艇型其流噪声总声压级低。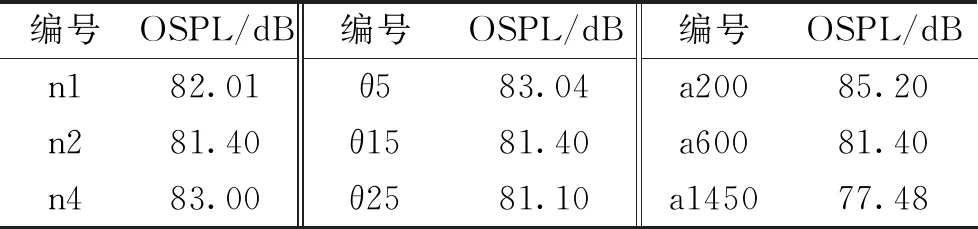

4 结论
