复选降噪自适应型MCKD方法研究

张旭龙，姜宏，章翔峰，李军，申勇

（新疆大学机械工程学院，乌鲁木齐 830047）

轴承作为风机等旋转机械正常运行的关键零部件，监测其运行状态及时检修和维护，将极大增加设备生命周期。但通常低故障响应的轴承滚动体故障信号受噪音影响，有效成份被淹没[1]使得提取特征有效性降低。故障诊断领域对高效分析方法的研究一直是难点和热点[2]。

常用的一些分析方法存在明显不足：经验模态分解（Empirical mode decomposition，EMD）[3]、局部特征尺度分解（Local mean decomposition，LMD）[4]容易产出现模态混叠，局部特征的辨识和分解能力有限。小波多尺度分析在信号处理过程中不丢失原有数据，有很好局部化特征分析能力[5]。利用这一特性，黄侨等[6]实现挠度信号温度效应分离，戴海亮等[5]实现数据干扰成份的剔除。小波方差能确定信号扰动强度和主周期[7]。峭度值能反应故障冲击成份强弱，值越大机械运转越偏离正常工况[8]，广泛应用于故障信号有效分量筛选。McDonald 等[9]在最小熵解卷积（Minimum entropy deconvolution，MED）基础上进一步改进提出最大相关峭度解卷积（Maximum correlation kurtosis deconvolution，MCKD），能对信号进行周期性分辨，在故障分析中能解卷积出周期性脉冲[10]。受背景噪声干扰MCKD对指定周期冲击信号增强和辨识能力有限、需要人为设定参数。潘洋洋等[11]提出互补集合经验模态分解（Complementary ensemble empirical mode decomposition，CEEMD）与改进最大相关峭度解卷积（Improve maximum correlation kurtosis deconvolution，IMCKD）相结合，对参数做预先设定的故障诊断方法，对MCKD做了一定程度优化，但还是美中不足。

本文结合上述研究，提出一种复选降噪自适应MCKD方法。首先利用小波多尺度分解得到故障信号高频分量，然后以峭度值最大准则复选出最优高频分量，最后结合小波方差自适应地确定MCKD参数。仿真、实验数据分析结果表明本文研究方法能有效提取特征，诊断故障类型。

1 最大相关峭度解卷积原理

相关峭度反应故障脉冲的存在和周期性[12]，表达式为

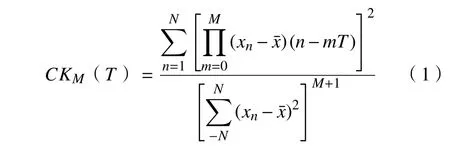
式中：M 为移位数；T 为冲击周期； xn为信号序列；为 信号的平均值； N为信号长度。

整个算法的核心是在相关峭度CK 值最大时，得到最优滤波参数。

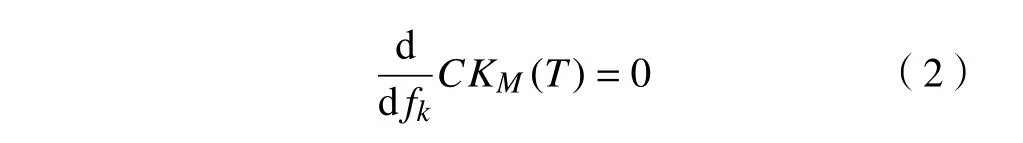
式中fk为滤波系数。

求解式（2）最终可以推导求出矩阵

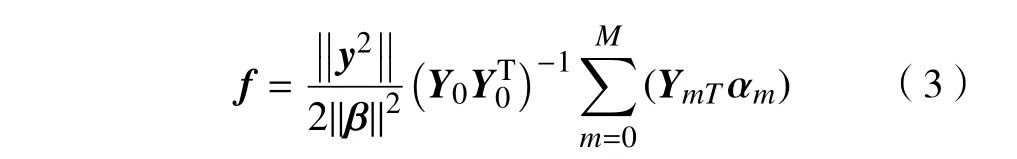
其中：

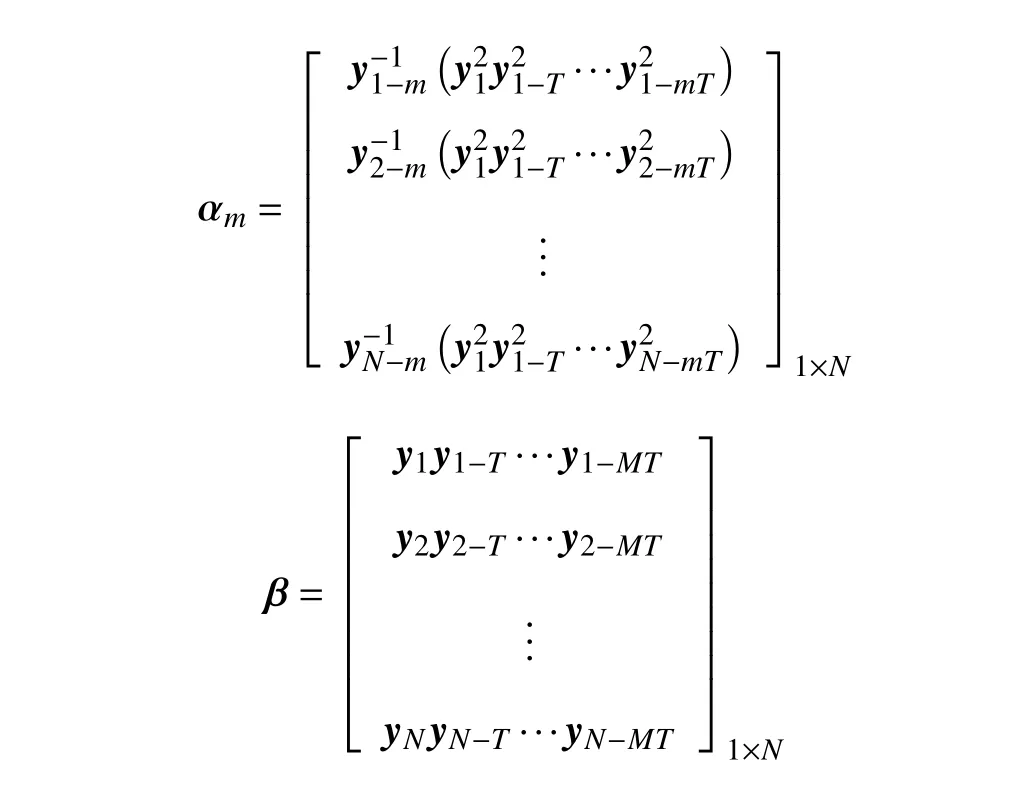
若输入信号 x(n)和系统 k(n)是卷积形式，噪音成份c (n)。则采样信号y (n)表达式为

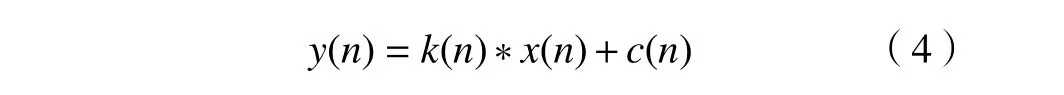
在忽略噪音影响下通过最优滤波器将所输入的信号从y (n)中滤出即

由式（4）、式（5）可知，MCKD方法在忽略噪音成份影响状态下建立，若噪音等干扰成分较强，MCKD滤波对于故障信号周期冲击的增强和辨识能力有限，并且不具备参数自适应选择。本文针对MCKD不足进行针对性优化，主要用强干扰低故障响应轴承滚动体故障信号进行算法改进的验证和说明。

2 复选降噪自适应MCKD方法

针对MCKD 不足所提改进方法流程如图1 所示。

图1 轴承故障诊断流程图

2.1 选取小波高频分量

小波多尺度分解先对数据间隔采样，然后小波系数与高频或低频滤波器卷积，表达式分别为：

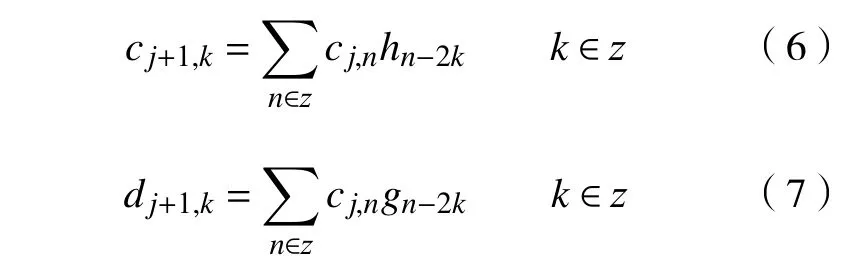
重构时先对数据间隔插零，再进行卷积从而将数据分解而又不改变原有数据的尺度，表达式为

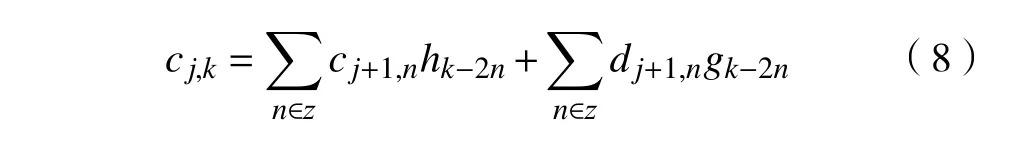
式中：j 为层数；h为低频滤波器；c 为低频系数；n为滤波长度；g 为高频滤波器；d 为高频系数。

轴承故障成份基本出现在高频段，为去除低频段噪音的干扰，选取高频分量作为故障诊断数据。

2.2 复选最优高频分量

多个高频分量之间，故障冲击的强度、周期性存在差异，需进一步从高频分量中复选出含有更高故障成份的分量。峭度是反应故障信号偏离正常工况程度的无量纲参数[8]，表达式为

峭度值越大，轴承越偏离正常的工作状态，信号中故障冲击成分越多，噪音干扰越少[8]。以峭度值最大准则选取信号高频分量，将进一步去除噪音成份的干扰。

2.3 MCKD参数自适应化

小波方差：小波系数平方值在b域上积分，表达式为

式中：a为低频系数；b为高频系数。

以采样点数对应小波方差值，所得最大主周期确定为MCKD滤波长度，能够将最大故障扰动及响应确定在同一冲击周期内。

要满足实际工程使用，算法必须实现自适应。MCKD中参数的设定非常重要，通常移位数M、滤波长度L靠人为经验设定，MCKD本身不具有自适应设定参数的能力。该研究中滤波器长度L由小波方差最大主周期确定；冲击信号周期T 由理论计算确定；M 一般不超过7，大于7将增大计算量、迭代失真、精度下降[13]，确定M=5。

3 仿真信号验证

引入一个常用轴承故障冲击模拟信号[14-15]，表达式为：

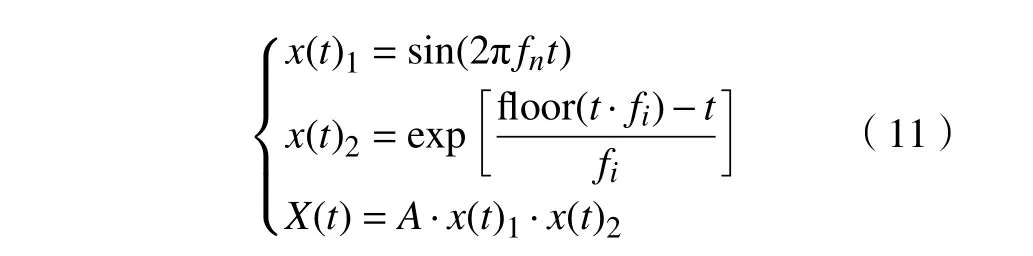
确定轴承固有频率 fn= 2000 Hz，故障频率 fi=100 Hz，冲击周期为1/ fi，幅值A=1，衰减指数B=192000。仿真信号的采样频率 fs=12800 Hz。真实故障含有大量噪音成份，对仿真加入信噪比为0.4的随机噪音，信号时域图和频域图如图2所示。

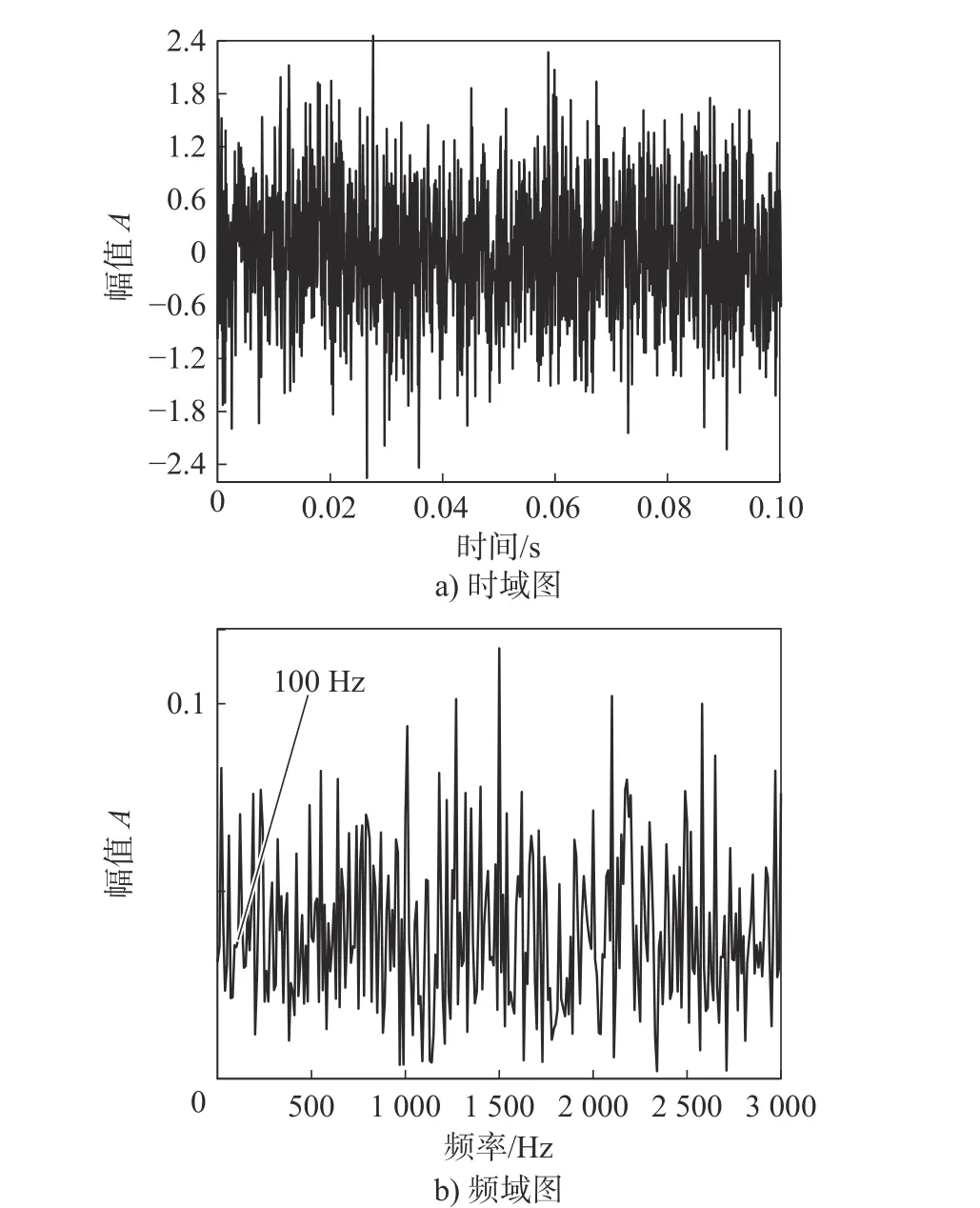
图2 故障仿真信号时域图和频域图

从图2中时域图可以看到信号幅值成份杂乱，没有明显规律性的故障成份显现出来，说明在噪音等因素的影响下，出现了轴承故障典型的调频调幅现象，故障冲击比较弱时，就会被淹没使得故障特征无法被有效提取。从图2中的频域图可以看到故障频率 fi=100 Hz 被完全淹没，也应证了这一点。按本文 研究方法分析得到高频分量时域如图3所示。

图3 仿真信号高频分量

通过峭度公式（9）得到仿真信号高频分量峭度数据如表1所示。

表1 仿真信号高频分量峭度

表1中峭度值差异较大，各高频分量故障冲击成份不同，有必要进行最优复选。峭度最大值对应高频分量d5，计算其小波方差确定MCKD滤波长度L=953。根据2.3节确定其他参数，滤波包络如图4所示，特征频率及其倍频显而易见，噪音等干扰因素基本滤除。

图4 滤波信号包络谱

通过轴承故障仿真信号验证，该研究方法在故障分析中特征频率提取及降噪效果明显。进一步通过实验数据分析，论证本文方法的有效性。

4 实验信号验证

采用Case Western Reserve University 公开轴承数据验证。试验台装置如图5所示。轴承故障直径0.1778 mm，由电火花加工技术在轴承上单点加工出故障，该实验使用加速度传感器采集振动信号。信号采样频率12 kHz，主轴转速为1797 r/min，轴旋转频率为29.95 Hz。

图5 试验平台

滚动轴承型号为6205-2RSJEM SKF，轴承参数如表2所示。

表2 轴承参数

根据故障经验式（12）[16]及表2参数得到轴承内圈故障频率为162.1 Hz、外圈故障频率为107.4 Hz、滚动体故障频率为141 Hz。

式中:fi为外圈故障频率； fo为 内圈故障频率； fb为滚动体故障频率；Z 为滚动体个数；d 为内圈直径；D 为外圈直径； α为接触角；Tn为轴承转速。

滚动轴承常见故障当中，滚动体故障微弱冲击被噪音淹没严重，属于强干扰低故障响应信号，故障特征最难提取。应用本文研究方法对轴承滚动体故障进行分析，原始信号时频域图如图6所示。

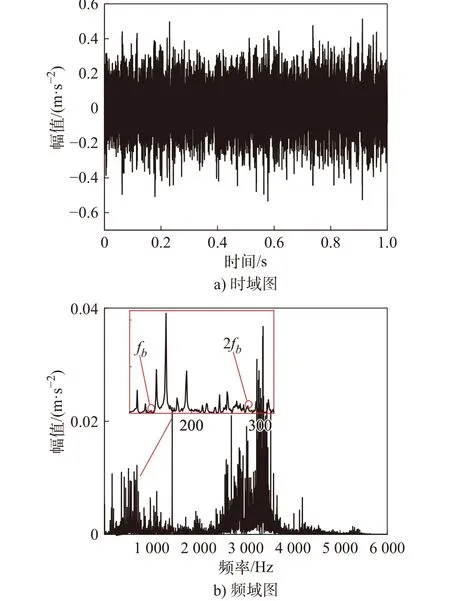
图6 滚动体故障原始信号时域图和频域图

滚动体故障原始信号时频域图中无法得到有效信息。频域当中特征频率基本被噪音成分淹没，信号冲击成份多且复杂更无法判断轴承故障类型。按所提方法对信号进行小波多尺度分解，得到故障信号高频分量如图7所示。

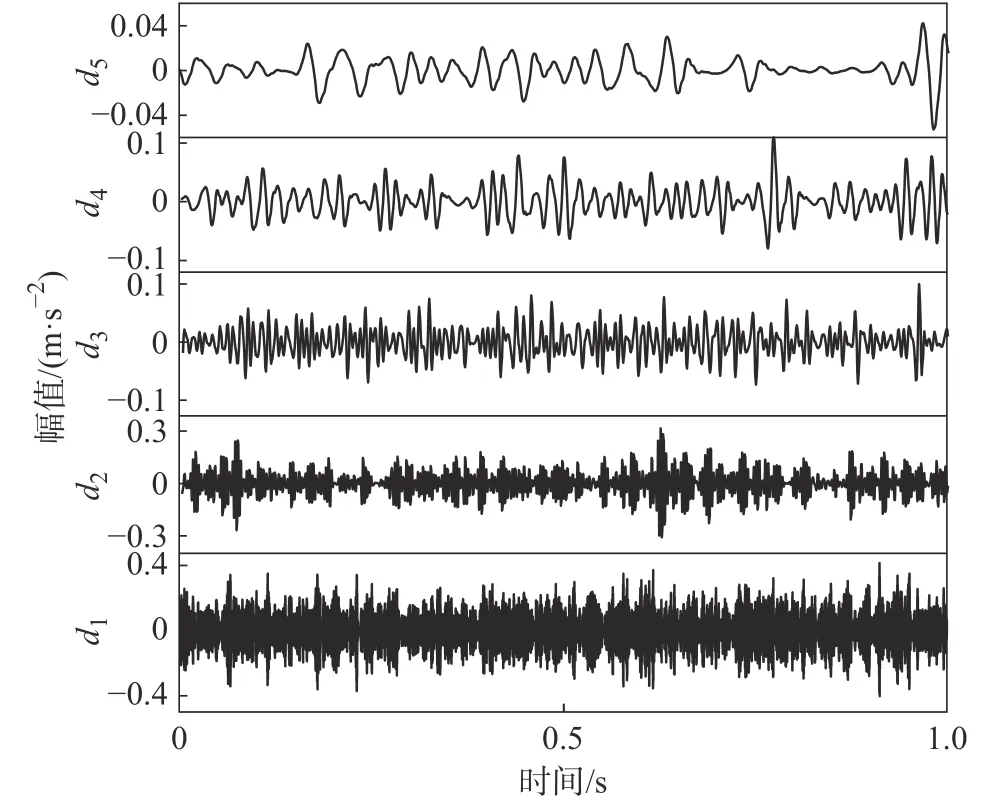
图7 滚动体故障信号高频分量

通过峭度公式（9）得到滚动体故障信号高频分量峭度数据如表3所示。

表3 滚动体故障信号高频分量峭度

如表3所示，选择峭度值最大的高频分量d5为最优分量。并进行小波方差计算,确定MCKD滤波长度L=777，复选降噪自适应型MCKD方法对高频分量d5降噪滤波后包络解调，得到故障频率提取结果如图8a）所示。为体现本文所提算法对MCKD故障信号指定周期冲击增强和辨识能力的提升，对滚动体故障信号采用相同参数直接进行MCKD单独滤波处理，故障频率提取结果如图8b）所示。

图8a）中噪音等干扰成份基本去除，滚动体故障特征频率140.6 Hz （与理论计算值141 Hz 非常接近）谱线明显，二倍故障频率287.1 Hz 显而易见，可以判断为轴承滚动体故障，同时能够识别出轴的转频为30 Hz（与计算值29.95 Hz 非常接近），本文方法能对低响应轴承滚动体故障实现有效诊断。

图8b）中，故障信号指定周期冲击未被明显增强，故障频率不易辨识，若故障频率为139 Hz（与故障频率理论计算值比较接近）,但所选频率周围存在其他非轴承滚动体故障频率干扰，无法判断轴承故障类型。表明对于弱响应轴承滚动体故障信号，单独使用MCKD方法不能实现较有效故障特征频率提取，验证了MCKD方法对强干扰故障信号指定周期冲击增强和辨识能力有限。

图8 滚动体故障信号滤波后包络谱

为了更加凸显本文所提方法降噪的优势，用以下分析方法进行再次对比：

1）对滚动体故障信号进行LCD分解，得到一系列内禀尺度分量（Intrinsic scale component，ISC），选取相关系数较大的ISC分量进行重构，再对重构信号用最大相关峭度解卷积处理[10]，重构信号滤波后包络如图9所示。

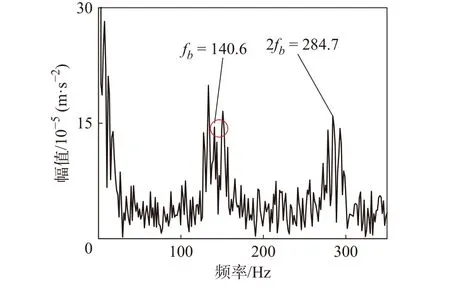
图9对比方法一、滤波包络

图9 中频率140.6 Hz（与理论计算值141 Hz 接近）幅值没有突显出来，并且噪音等因素产生的干扰频率大量存在，难以判断轴承故障类型，不如本文所提方法。

2）对轴承滚动体故障信号进行CEEMD分解，选取峭度值最大的3个本征模态函数（Intrinsic mode function，IMF）重构，对重构信号进行最大相关峭度解卷积处理[11]。滤波后包络如图10所示。

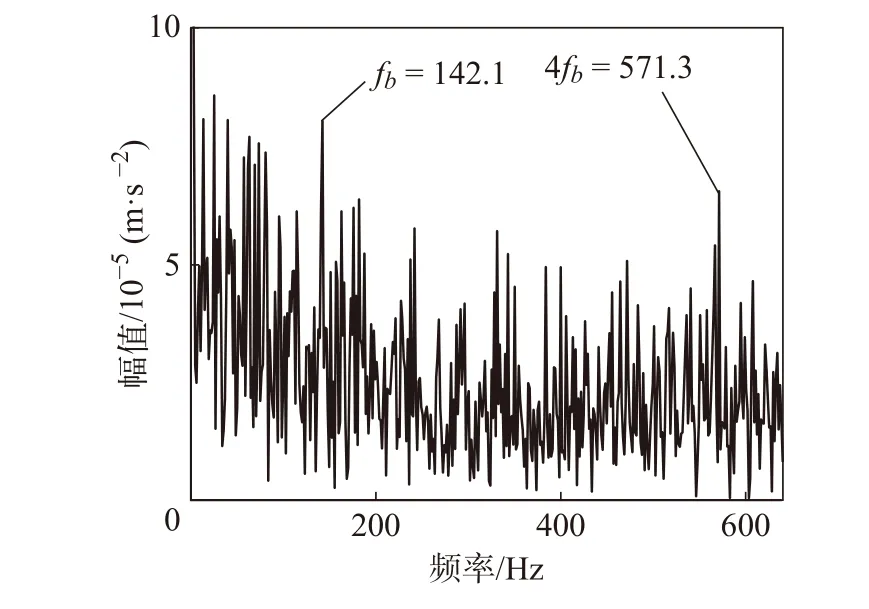
图10对比方法二、滤波包络

图10 中故障特征频率没有分解出来，虽然能够找到与故障理论计算频率值141 Hz接近的频率，但频谱中混杂大量干扰成分，噪音等成份没有消除。无法判断轴承故障类型。

通过以上对比，表明本文所提方法不仅实现自适应而且对滚动体故障信号指定周期冲击提取和辨识能力明显增强。因此本文提出的方法更具优势，可以实现更加精确的诊断。

使用本文所提方法对轴承内外圈故障进行分析，结果如图11所示。

图11故障信号滤波包络

图11 a）中内圈故障特征频率162.6 Hz （与理论计算值162.1 Hz非常接近）及其倍频325.2 Hz、486.3 Hz、647.5 Hz 谱线都非常明显，能够判断为轴承内圈故障。图11b）中外圈故障特征频率108.4 Hz（与理论计算值107.4 Hz非常接近）及其倍频216.8 Hz、323.7 Hz、432.1 Hz谱线都非常明显，能够判断为轴承外圈故障。

综上，本文所提方法能够对弱故障响应的轴承滚动体故障和轴承内、外圈故障实现有效的诊断。此方法对于轴承作为易损件的旋转类机械设备，实现状态监测和预警具有很高的研究和使用价值。

5 结论

通过对本文提出的算法进行仿真及实验数据分析，得出以下结论：

1）对轴承故障进行小波多尺度分解，选择冲击成份更丰富的高频分量，有利于故障诊断。依据峭度值最大准则复选出最优高频分量，能够最大程度上保留故障冲击和排除其他因素干扰。通过复选弥补了MCKD方法对故障信号周期冲击增强和辨识能力有限的缺点。

2） 结合小波方差最大主周期自适应确定MCKD参数。使MCKD方法对故障特征的提取更加高效、具备自适应能力。

3）本文研究方法降噪能力较强，能够实现滚动轴承不同类型故障特征频率的准确提取。