重型拖拉机液压机械无级变速器箱体疲劳寿命分析

2022-02-13孙晓旭鲁植雄陈元

机械科学与技术 2022年12期

孙晓旭，鲁植雄，陈元

（南京农业大学工学院，南京210031）

随着我国农业机械化水平的不断提高，拖拉机作为一种重要的农用机械越来越多的出现在我国的农业生产中。变速器是拖拉机动力总成的重要组成部分，主要装置包括变速器箱体、齿轮、泵马达、轴承等，是一个十分复杂的系统，在其工作过程中不可避免的受到内外部激励的作用。当拖拉机在耕地、运输等典型工况下作业时，变速器呈现着不同的载荷特性。一方面，变速器传动系统所产生的交变载荷通过轴承作用在变速器箱体上，另一方面，在车辆行驶过程中，会受到路面的随机激励作用，且这部分的动态载荷可能会比稳态工况下的载荷要高几倍甚至十几倍[1-3]。针对拖拉机来说，变速器质量较大，而且与汽车不同，无车架承载，所以路面所带来的振动激励更不可忽视。在这种两种激励的共同作用下，箱体的动态响应十分复杂。如果变速器箱体发生破坏，不仅会影响到整车性能，甚至也会影响到驾驶人的生命安全[4]。因此，为保证拖拉机持续高效的作业能力，在设计之初对变速器箱体进行寿命预测尤其必要[5-6]。

针对变速器箱体的寿命可靠性问题，国内外诸多学者都做了不少的研究。Barke等[7]采用不同的理论模型和试验数据，分析了轮轨振动对车辆和轨道部件疲劳寿命的影响。高娜等[8]通过多体动力学仿真获得轴承孔的动态力，分析了齿轮箱壳体的动态响应。该模型能够获得难以直接测量的轴承孔激励，但忽略了路面激励的影响。陈婷等[9]考虑了道路激励对壳体的影响，通过建立虚拟样机试验台和实车试验采集加速度信号，获得了箱体车架连接处载荷，对变速器壳体的疲劳进行了分析。邓国红等[10]基于静力学分析结果，应用Miner 线性积累疲劳损伤理论进行了箱体疲劳寿命分析，并对局部区域进行了优化设计，但忽略了动态激励的影响。

本文针对上述问题，基于虚拟样机技术，提出了一种针对拖拉机变速器箱体的一种疲劳寿命预测方法。首先，基于Adams建立了变速器的刚柔耦合虚拟样机模型，结合典型工况负载计算和田间实测路面激励获取了变速器箱体的载荷历程；然后通过有限元分析，得到变速器箱体的动态响应；其次，综合考虑变速器箱体结构参数，受载特点，表面工艺，材料特性等因素，重新拟合了箱体结构S - N 曲线；最后，基于Miner 线性累计损伤理论对变速器箱体进行了疲劳寿命预测。

1 变速器系统刚柔耦合模型的建立

液压机械无级变速器是基于功率分流原理将机械功率和液压功率并联传动以实现高效的无级变速，其传动系统主要由行星轮系、定轴轮系、泵、马达、离合器等组成。本文研究的HMCVT 传动系统由3个行星齿轮机构（P1、P2、P3），5个离合器（C1、C2、C3、CV、CR），一个定量马达，一个变量泵，6根轴（Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ），8对定轴啮合齿轮副（i1、i2、i3、i4、i5、i6、i7、i8）组成。分3个工作段位，传动原理如图1所示。

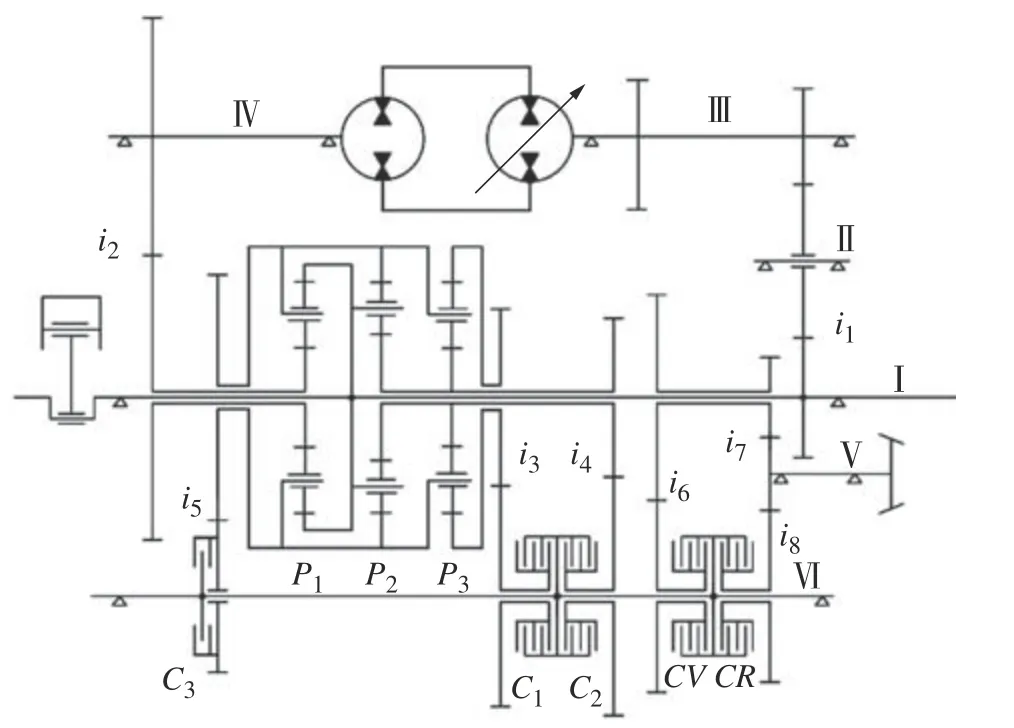
图1 液压机械无级变速器传动原理图

根据HMCVT传动原理图，利于UG 三维建模平台建立变速器箱体齿轮传动系统实体模型。将建立好的三维模型导入到Adams中，添加相应运动副。为了更好的模拟齿轮传动，在啮合的齿轮之间添加接触力。在输入轴（Ⅰ轴）添加转动驱动，模拟发动机输入，在马达轴（Ⅳ轴）添加转动驱动，模拟马达输入。输出轴上添加与转速方向相反的力矩来模拟变速箱负载。为了更真实的模拟变速器箱体材料对振动激励的作用效果，本研究将传递振动的变速器箱体进行柔性化处理。采用Hypermesh 以四面体单元对变速器箱体进行网格离散，并根据Adams里变速器箱体与其余刚性体连接位置坐标建立硬点，利用rigids单元在连接点位置创建刚性连接区域。模拟变速器在拖拉机中实际安装位置，简化发动机模型与分动箱模型，导入Adams中进行装配。在发动机与分动箱上添加移动副，将实测拖拉机前后轮地面激励以生成的样条曲线的形式分别加载在与HMCVT 箱体相连的发动机和分动箱模型的移动副上，模拟路面振动激励。然后在Adams里将箱体与发动机和分动箱连接螺栓孔硬点位置添加固定约束从而将箱体的柔性体与发动机和分动箱的刚性体相连接，实现力的传递。在轴承外圈与箱体轴承孔之间添加固定约束，轴承滚子与内外圈添加接触约束，轴承内圈与轴添加固定约束，从而实现内部传动系统刚性体与箱体柔性体之间的力的传递。建立好的虚拟样机仿真模型如图2所示。

图2 变速器虚拟样机仿真模型

2 拖拉机变速器载荷分析

在拖拉机作业过程中，变速器箱体主要承受两大激励：1）扭矩载荷，箱体支撑着整个变速箱内部的传动系统，在拖拉机工作过程中，由发动机输入的扭矩载荷通过齿轮传动由传动轴经两端轴承传递到箱体的轴承座；2）由于路面不平度所带来的路面激励。拖拉机变速器箱体位于拖拉机驾驶室下方，前端与发动机相连架在前桥上，后端与分动箱相连架在后桥上，与汽车不同，为承载式箱体，无车架支撑。其次拖拉机变速器重量也较大，所以在行驶过程中，路面不平度所带来的振动激励也会引起箱体产生复杂的动态响应。由于拖拉机作业工况复杂，作业环境恶劣，在这两大激励的共同作用下，极易导致箱体发生疲劳破坏。由于拖拉机工作情况差别很大，不同工况下变速器箱体所呈现的载荷特性不同。因此，本文对犁耕和运输两种典型作业工况进行载荷分析。

2.1 典型工况扭矩负载

2.1.1 运输工况

当拖拉机处于运输工况时，由于拖拉机的作业速度比较低，迎风面积较小，因此空气阻力和加速阻力可以忽略[11]。而本文研究拖拉机在平路上行驶，所以拖拉机主要所受到的阻力为滚动阻力。拖拉机在平坦道路上受到的滚动阻力为

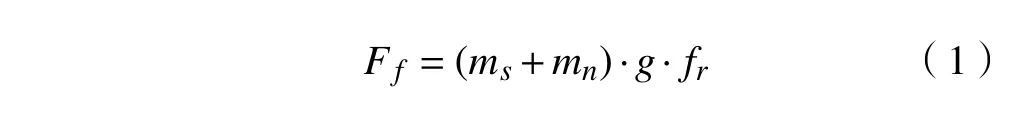
式中： ms为拖拉机质量， kg； mn为挂车质量， kg；g 为重力加速度，9.8 N/kg； fr为滚动阻力系数。

此时拖拉机负载为

2.1.2 犁耕工况

当拖拉机处于犁耕工况时，同样忽略空气阻力和加速阻力，此时拖拉机所受阻力为犁耕阻力和滚动阻力。所受到的犁耕阻力为

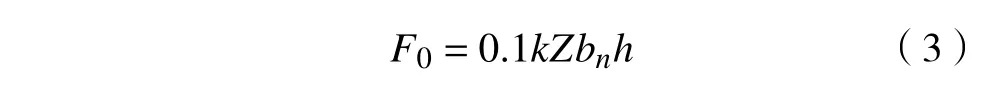
式中：F0为犁耕阻力，N；k 为土壤犁耕比阻；Z 为犁铧数；bn为单个犁体耕作幅宽，cm ；h为耕深，cm 。

拖拉机所受到的总阻力为

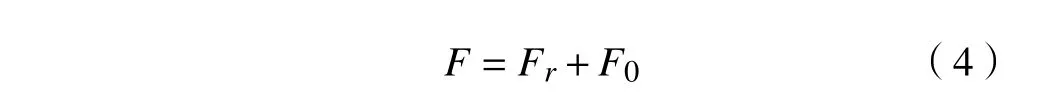
此时拖拉机驱动轮负载为

式中r 为拖拉机驱动轮半径，m。

拖拉机结构质量为8500 kg，当拖拉机处于运输工况时，所带挂车质量为1500 kg，作业速度为10 km/h，滚动阻力系数为0.05；当拖拉机处于犁耕工况时，犁具型号为1L-530，质量为520 kg，单个犁宽为30 cm，耕深为25 cm，犁耕比阻为50 kPa，作业速度为8 km/h。拖拉机驱动轮半径为0.9 m，后桥减速比为3.8，轮边减速比为7.07。把以上参数代入计算可得表1。

表1 变速器扭矩负载

2.2 拖拉机路面振动激励测试

为获取拖拉机作业过程中所受到的路面激励，作为虚拟样机的路面输入，采用LMSTest.Xpress测试系统对土路，道路两种拖拉机典型路况进行田间实测，获取拖拉机四轮中心处的振动激励。测试系统由单向加速度传感器，数据采集前端，SCM-V8数据输入模块组成，试验设备及测量点位置如图3所示。为提高数据采集精度，对数据采集前端进行传感器灵敏度等相关设置，对采集得到的数据进行去趋势项，滤波等处理[12]。根据Nyquist-Shannon 采样定理，采样频率至少应为分析信号中最高频率成分的2倍[13]。在实际工程应用中常取3～5倍，经计算，本实验中设置采样频率为200 Hz。

图3 试验设备及测点

本次试验场地为南京溧水区江苏现代农机科技示范园。分别在拖拉机道路，土路两种工况下进行试验，整个测试过程遵循拖拉机操作规范，试验过程参照GB/T14225-2008对作业环境及作业质量进行检测。每种工况均进行3次试验取平均值。拖拉机路面激励测量结果如图4所示。拟负载，将实测拖拉机前后轮路面振动激励以表格方式导入Adams 中，生成spline 样条曲线分别添加到变速箱前后发动机与分动箱模型的移动驱动上模拟路面振动。设置仿真时间为15 s,仿真步数为8 000 步，对虚拟样机模型进行仿真。提取变速器箱体各轴承孔中心处XYZ 方向的动态激励，为便于下文对箱体进行动力学分析，截取稳定后的10 s（5 ～ 15 s）作为载荷谱。这里仅列出输出轴左轴承孔处载荷如图5 所示。各轴承孔3 个方向载荷最大值见表2。

表2 各轴承孔载荷最大值

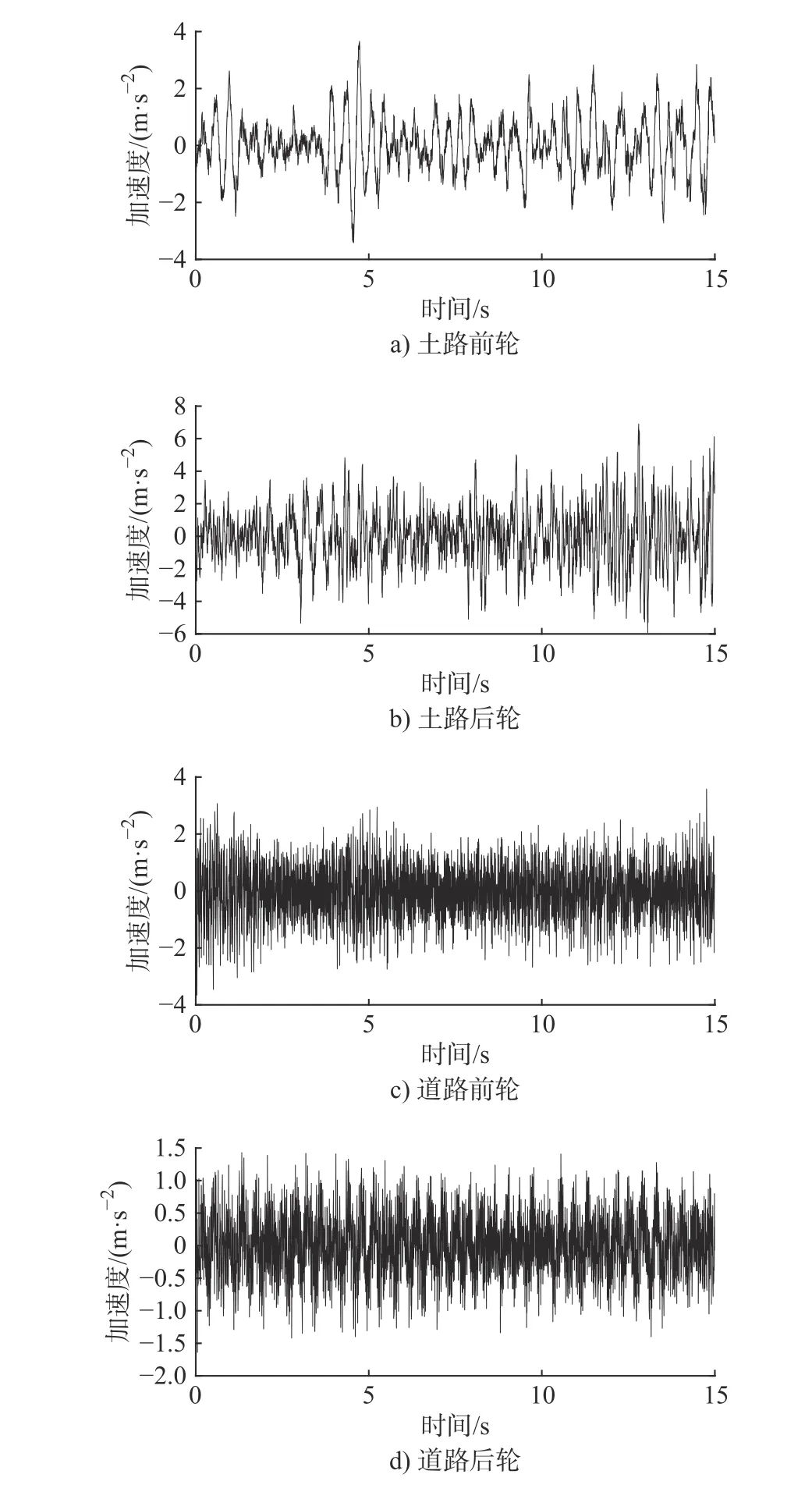
图 4 拖拉机轮心路面激励

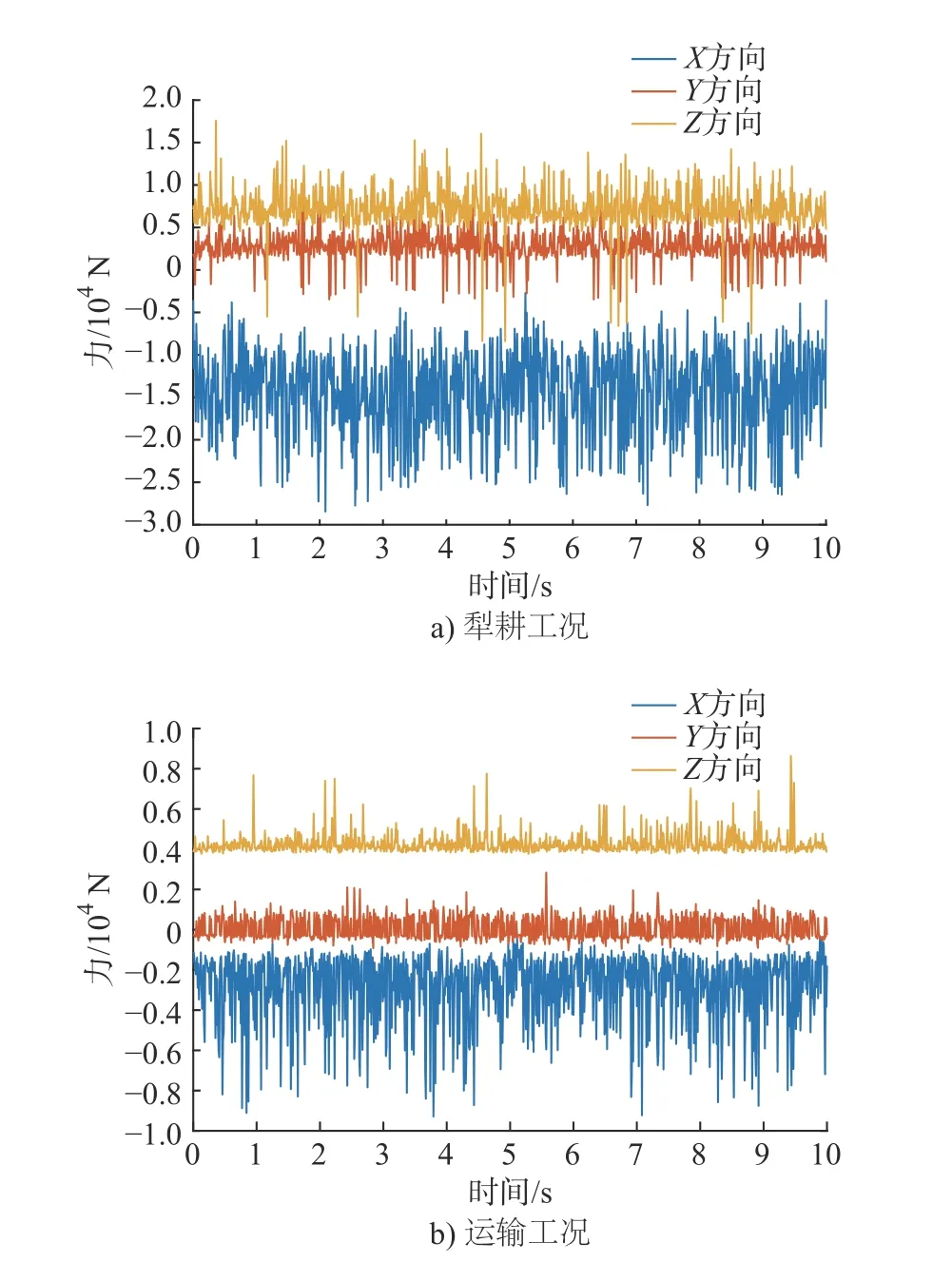
图 5 输出轴左轴承孔动态载荷

2.3 变速器箱体动态载荷仿真计算

将前文计算所得扭矩添加在变速器输出轴模

3 动态激励下变速器箱体的瞬态响应

3.1 有限元模型的建立

网格质量是获得准确的有限元计算结果的基础，所以本文借助Workbench 强大的前处理功能对变速器箱体进行网格划分。首先对变速器箱体进行预处理，简化对结构没有影响的小孔，圆角等，这样既可减小有限元计算工作量也不会影响计算结果[14-15]。随后对模型进行网格划分。设置变速器箱体材料HT250的属性，弹性模量为1.38×1011Pa，泊松比为0.26，密度为7280 kg/m3。设置网格形式为四面体单元，设置网格最小单元尺寸为10 mm。划分网格后，变速器箱体中有限元单元数目为个237765，节点数目为404556个，网格单元最小雅克比为0.7。根据变速器箱体实际情况安装情况在HMCVT 箱体前后螺栓连接孔位置添加固定约束。将各轴承座处的复合动态激励离散化后，以表格的形式导入Workbench 中，轴向载荷添加在轴承孔挡肩面上，径向载荷采用Workbench 轴承载荷的形式添加在轴承孔圆周面上，建立的有限元模型如图6所示。

图6 HMCVT箱体有限元模型

3.2 有限元分析

对前文载荷结果进行分析，犁耕工况下拖拉机变速箱所受到的载荷明显大于运输工况下的载荷，而且，通过企业调研结果，本型号拖拉机的作业工况90%为犁耕，所以后文以犁耕工况为例进行分析。

对添加载荷与约束后的HMCVT 箱体进行动力学分析，得到有限元分析结果如图7所示，其中图7a）为HMCVT箱体应力云图，图7b）为最大应力位置局部放大云图，图7c）为最大应力节点处的应力时间历程。从图7中可知，HMCVT箱体应力集中区域为变速器箱体中间隔板处，惰轮轴支撑轴承座处，前后箱盖轴承孔处以及变速器箱体与取力泵连接处。多为箱体受载位置，分析合理。因为最大应力出现在变速器箱体惰轮轴支撑轴承座位置（节点160650），最大应力出现在4.48 s，其值为121.2 MPa，10 s内的平均应力为52.2 MPa。虽然最大应力小于壳体材料的强度极限，但这种交变应力是结构疲劳破坏的重要原因[16]，所以需要重点关注其疲劳损伤情况。且从结构上分析，此处为一悬臂肋板，所以此处为变速器箱体危险部位，后文将以此处作为研究对象进行疲劳寿命分析。

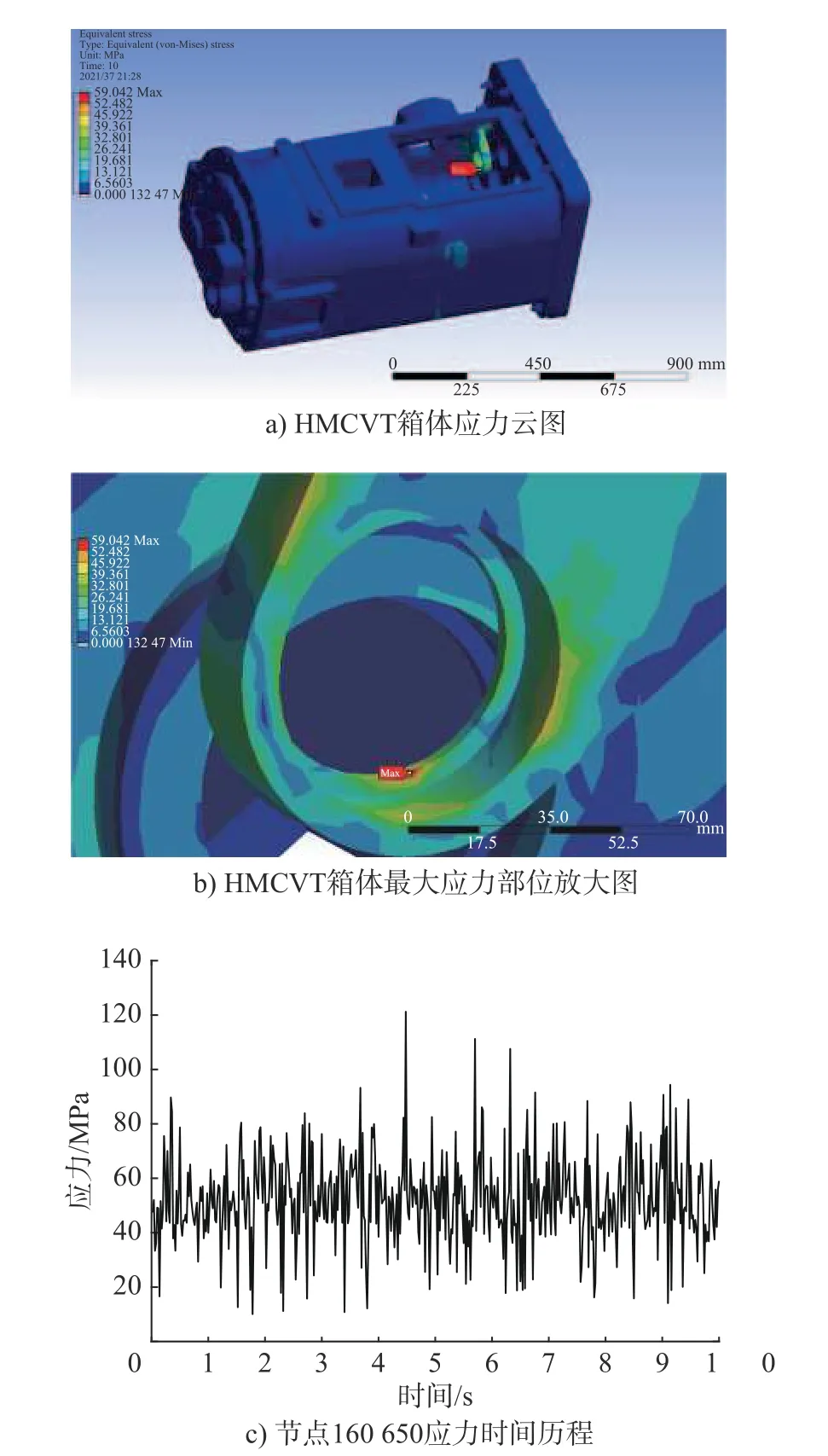
图7 HMCVT箱体有限元分析结果

4 变速器箱体的疲劳寿命分析

4.1 变速器箱体的S - N 曲线

S - N 曲线是作为计算结构疲劳寿命的基础，材料的S -N 曲线一般可以通过前人对试样进行疲劳试验，查阅材料性能手册获得，但是，对于同一材料的不同构件来说，随着构件的结构、加工工艺、尺寸大小的不同，S -N 曲线也会随着改变。因此，准确拟合构件的S -N 曲线是正确预测结构疲劳寿命的关键。本节基于变速器箱体实际工况应力特点，结合所研究变速器箱体实际结构参数，材料特性，表面质量等因素。对变速器箱体S - N 曲线进行了修正。4.1.1 S - N 曲线的近似估计

S - N 曲线常用的数学表达式为

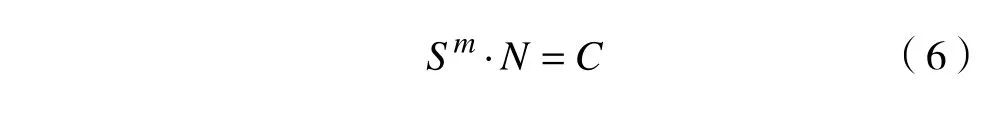
式中： m和C 均为材料常数。

对式（6）两边取对数，有m lg S+lg N=lg C。通常假定寿命 N=103时，S103=0.9Su， N=107时仍未被破坏，则可无限循环，即S107=Sf，可得：

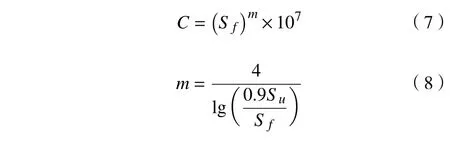
查阅文献可得变速器箱体材料HT250的强度极限为 Su为 250 MPa，疲劳极限 Sf为140 MPa。根据式（6）～式（8）可得HT250的S - N 曲线为

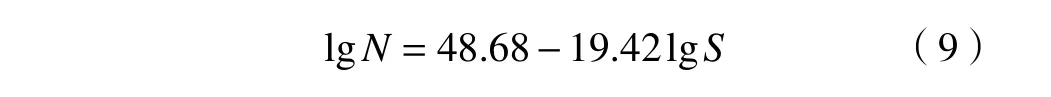
4.1.2 S - N 曲线的修正

1）应力集中的修正

相比于标准光滑试样，变速器箱体结构的几何不连续，圆角等结构特征更容易产生应力集中，从而使得局部应力较高，疲劳强度降低。所以需要考虑应力集中系数Kt的影响，应力集中系数Kt为应力峰值σmax和名义应力σn的比值，即

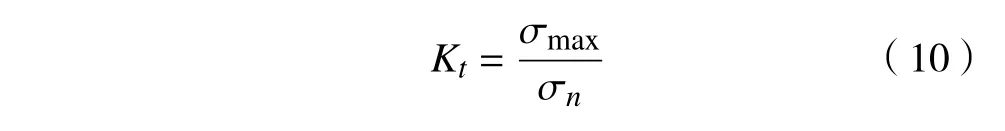
名义应力σn可通过对有限元计算结果进行分析，定义积分路径并沿应力路径积分获得。

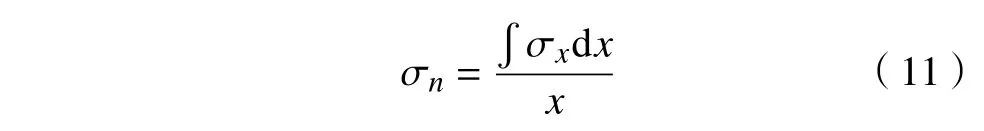
式中 x 为积分路径长度，mm。

由上文有限元分析结果可得，变速器箱体最大应力点位于惰轮轴左轴承座处，对最大应力点截面进行分析，定义与最大应力的切向的垂直方向为应力积分路径方向，提取路径上应力分布。为了追求应力分布曲线的高精度拟合，诸多学者提出了多种曲线拟合模型，本文采用文献[17]中提出的拟合公式对危险节点处的应力分布进行拟合计算。积分路径及应力分布如图8所示。将所得结果代入式（10）和式（11），计算得到应力集中系数Kt=2.01，名义应力σn=60.44 MPa，积分路径长度x = 9.42 mm。

图8 应力积分路径及分布

2）尺寸大小的修正

构件的尺寸越大则出现缺陷的概率越高，而疲劳强度是具有局部性的，所以构件的尺寸越大往往会使得疲劳强度降低。在相同加载条件及相似的几何特征下，疲劳尺寸系数ε 表示大尺寸试件的疲劳强度与小尺寸试件的疲劳强度的比值。可通过L/G公式求解某相对应力梯度下的疲劳尺寸系数，即

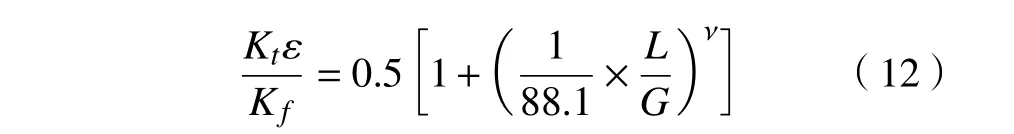
式中：Kf为疲劳缺口系数；L为最大应力长度；G 为相对应力梯度；ν为材料参数。

相对应力梯度G 为应力沿其增长（下降）最快方向的变化率与应力峰值的比值。疲劳缺口系数Kf可通过应力集中系数计算，即

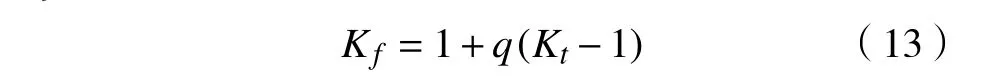
式中q 为缺口敏感系数，可由Neuber 公式求得

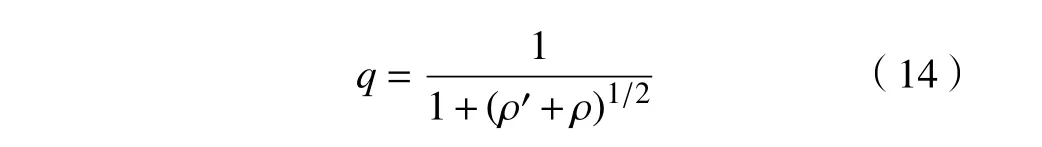
式中： ρ为缺口半径，mm； ρ0为Neuber 参数，取0.85。

将所得的应力分布结果代入式（12）～式（14）进行计算，HMCVT 箱体尺寸系数ε = 0.6，Kf=1.15。

3）表面质量的修正

构件的疲劳裂纹一般都是从表面开始产生的，所以构件的表面质量对疲劳强度有很大的影响。表面状态系数考虑表面的加工，腐蚀以及强化系数，用β表示根据文献[18]确定取β 为1.22。

结构S - N 曲线与原材料S - N 曲线的关系为

得到的变速器箱体结构S - N 曲线为将修正前后S -N 曲线绘制在同一双对数坐标系中，如图9所示。观察曲线可知，变速器箱体结构的S - N 曲线对材料的S - N 曲线较有一定程度的修正，结构的疲劳极限有了明显的降低，以原材料S - N曲线估计疲劳寿命较为保守。

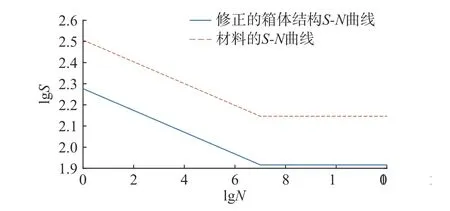
图9 原材料与修正后结构的S - N 曲线

4.2 箱体疲劳寿命计算

线性累积损伤理论是工程中应用最广泛的疲劳损伤理论[19]。线性疲劳累积损伤理论认为，构件在载荷循环的作用下，其疲劳损伤是可以线性叠加的，当损伤达到某一程度时，构件就会疲劳破坏。结构疲劳累积损伤可以表示为

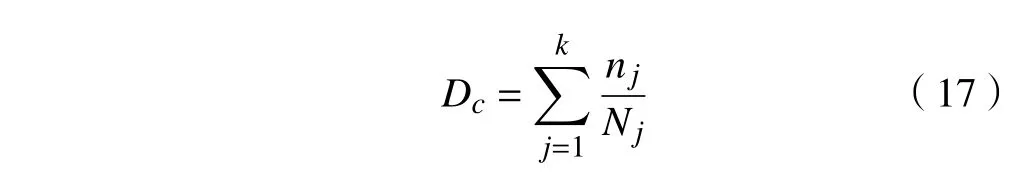
式中： Dc为构件的累积损伤量； nj为第 j个应力幅值的循环次数； Nj为第 j个应力幅对应的S - N 曲线的极限循环次数。

采用雨流计数法对HMCVT 箱体犁耕作业下危险节点的应力时间历程进行统计计算，得到应力幅值，应力循环次数及应力均值的关系如图10所示。将统计得到的应力幅代入拟合的S - N 曲线，即可求得每个应力幅的极限循环次数。将得到的应力幅值循环次数和极限循环次数代入式（17），计算可得在犁耕作业下的疲劳累积损伤量为D = 4.8353×10-8，所以变速器箱体的疲劳寿命为T = （1/D）×10 s = 57447 h。根据企业提供的调查结果，该大马力拖拉机90%作业工况为犁耕作业。拖拉机报废年限为15 y，按每天作业6～ 8 h，报废时限为43800 h。结果表明，所设计的变速器箱体较为保守，满足全寿命使用要求。