优化VMD与CNN在齿轮箱故障诊断应用研究

2022-02-13郗涛杨威振

机械科学与技术 2022年12期

郗涛，杨威振

（天津工业大学机械工程学院，天津 300387）

在机床主轴的传动过程中，齿轮箱占有着举足轻重的地位，其运行状态更是关系到整个设备的运行状态。由于齿轮箱所处的工作环境相对恶劣多变[1]，且其主要是由高速化、高精度化与复杂化的齿轮与轴承构成，所以对早期的齿轮箱故障检测很有必要。整体方案是首先对齿轮箱不同运行状态的振动信号进行提取与分析，最终判断出齿轮箱的故障类型。

在进行振动信号的提取与分析中，常采用自适应分解方法，该方法在对非线性、非平稳的以及多分量耦合信号的处理中表现优异。国内外学者在故障诊断中常采用经验模态分解（Empirical mode decomposition，EMD）来提取故障信号。EMD是由Huang[2]提出，在非平稳信号中表现良好后，已经被应用于各个领域，但仍存在端点效应和模态混叠的现象，且该缺陷是EMD的固有缺陷。周陈林等[3]通过提出EMD分解与形态奇异值分解相结合的故障特征提取方法，很大程度上降低了EMD分解的过分解和端点效应，但欠分解与模态混叠的现象仍是没有得到改善。李思琦[4]利用集合经验模态分解（Ensemble empirical mode decomposition，EEMD）将白噪声信号添加到需要分析的信号中之后进行EMD分解，在一定程度上能够抑制模态混叠现象的出现，但是噪声信号的加入使得系统对信号处理的工作量增大，且容易分解出无关变量甚至虚假变量。Li[5]使用的局部均值分解（Local mean decomposition，LMD）虽然能够解决EMD的欠分解与过分解问题，但是端点效应与模态混叠现象仍然存在。Wang[6]使用本征时间尺度分解（Intrinsic time scale decomposition，ITD）对独立的旋转分量进行分解且分解出的瞬时频率具有物理意义，但本身固有缺陷容易导致分解存在失真。而优化的模态分解（Variational mode decomposition，VMD）算法凭借其强大的自适应性、可重构性、平滑滤波特性，可为上述问题的解决提供新的技术方案。

在深度学习方面，文献[7-10]分别利用支持向量机、深度置信网络、时频输入的卷积神经网络以及生成对抗卷积神经网络对轴承或齿轮的进行故障诊断，不同的故障之间要有一定的关联程度，所以上述方法很难对故障进行精确地诊断。本文使用VMD分解完成的故障信号作为卷积神经网络（Convolutional neural network，CNN）数据输入，解决了不同故障之间需要有关联的问题，并且能够提高CNN对于故障信号的识别，之后在考虑多因素的故障特征情况下完成故障诊断。

CNN 在图像识别与分类中取得了良好效果，也被越来越被广泛地应用于机械振动领域。对振动信号的识别与分类是其实现故障诊断的重要手段。但在CNN 模型的初始化中需要对预定的CNN 参数进行确定，参数的选择直接关系模型的优良。本文在对CNN 参数优化完成的基础上，并进行优化结果比较。

综合上述问题，本文针对齿轮箱的故障提出了优化的VMD与CNN相结合的故障诊断方法的研究，该方案经过数据的对比以及实验的验证，证明该方案的可行性与有效性。

1 基本理论

1.1 变分模态分解

变分模态分解是Dragomiretskiy 等[11]在2014年提出的一种新型非递归式的自适应分解方法。

VMD的分解过程本质上是对约束的变分问题的求解过程。将原始信号 f非递归地分解为K 个有限带宽的固有模态分量（Intrinsic mode function，IMF）分量uk(t)，其表达式为

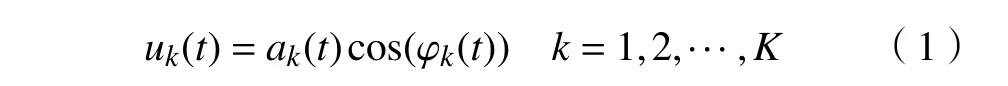
式中：t 为时间序列；ak(t)为非负的包络线；φk(t)为相位。

建立变分问题，通过Hilbert 变换，获得的解析信号及单边谱为

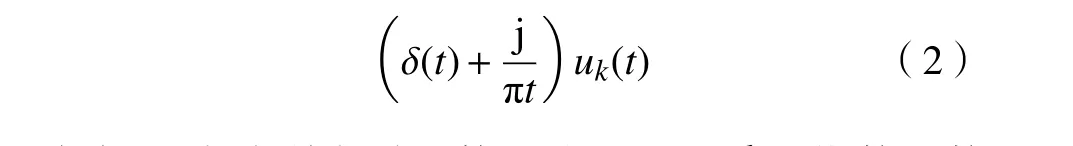
式中 δ(t)为狄利克雷函数。然后通过乘以指数函数e-jωk(t)，把各模态的中心频段移到基频带上

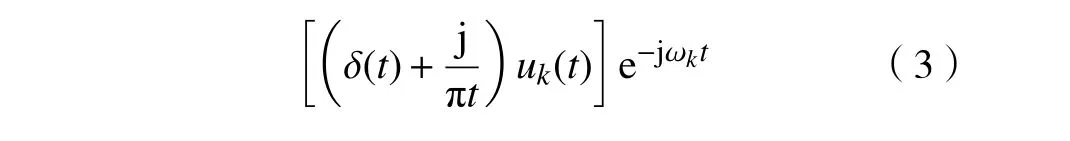
再利用调制信号 L2范数的平方来估算各分量的带宽，约束条件是使其所有带宽之和最小，即

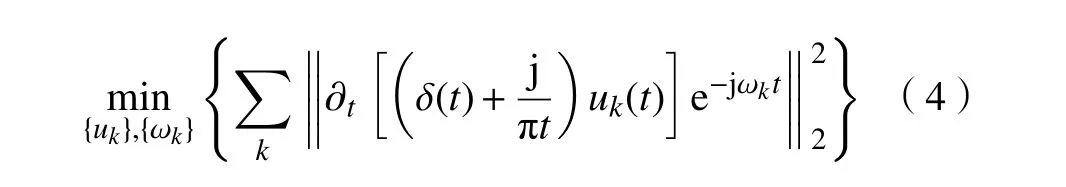
式中{ ωk}={ω1,···,ωk}为各分量的中心频率。

将所有子信号相加，可以得到原始信号f，即

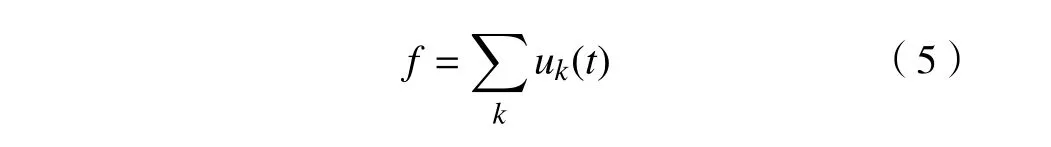
在以上模型基础上通过引入二次项惩罚因子α以及Lagrange 乘子λ，将变分约束问题转变为非约束变分问题，其中增广Lagrange函数为

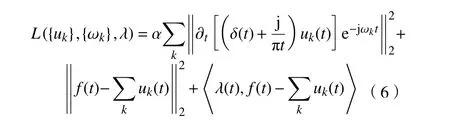
该算法的具体应用流程图如图1所示。

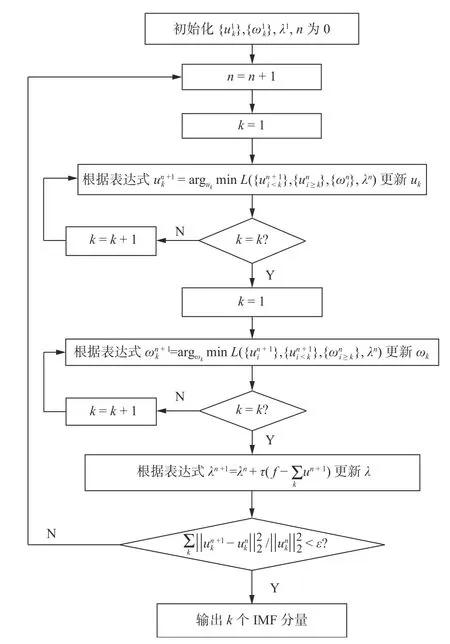
图1 VMD 算法应用流程图

1.2 VMD算法优化

在VMD的参数初始化过程中，首先是调整惩罚因子α 和分解个数K 这两个重要参数。

实验探究发现，若K 值选择过于小于最佳值，会出现欠分解现象，即信号中的多个有效成分会同时分布在一个模态分量中。反之，若K 值的选择过于大于最小值，则会出现过分解的现象，信号在经过VMD分解时会分解出无关变量甚至虚假变量。

二次项惩罚因子 α的引入可以用来降低高斯噪声的干扰，以及同Lagrange乘子的引入可以将VMD算法的约束性变分问题转化为增广Lagrange方程以便于求解。在实际应用过程中主要是在影响分解出的各模态频谱的带宽以及算法的收敛程度。此外，不合适的惩罚因子 α的选择，会造成计算的工作量以及计算耗时都会很大程度上的增加。

在VMD参数选择以及优化中，目前尚未有统一的理论，更没有最好的方案。本文将采用鲸鱼优化算法（Whale optimization algorithm，WOA）对VMD参数进行优化并且将峭度作为参数优化的评价准则，从而建立WOA-VMD参数优化模型。

1.2.1 峭度准则

峭度[12]（M）是反映振动信号分布特性的数值统计量，是一种归一化的4阶中心距。

式中：x(t)为瞬时幅值； x¯为振幅均值； p(x)为概率密度； σ为标准差。

不同的峭度对应着不同的M 值，其不同的M 值都对应着不同的实际意义，在峭度曲线中，定义M =3或接近3时曲线具有正常峰度（零峭度）；当M ＞3时，此时分布曲线具有正峭度，说明观测值的密集程度较高且概率密度的集中程度较高；反之，当M ＜3时，此时分布曲线具有负峭度，说明观测值的密集程度较低且概率密度的集中程度较低。

不难发现，在齿轮箱无故障运转时，由于机械设备的运动特性以及环境的综合影响，会造成振动信号的概率密度分布接近正态分布，此时的峭度值M ≈3。当正态曲线出现集中或分散的情况时，若概率密度分布曲线扔保持正态分布，则小幅值的概率密度会增加，根据式（7）可得，此时的峭度值会发生改变。M 的绝对值越大，设备运转越偏离正常状态，若M ＞8，则设备较大可能性的出现了严重故障。

1.2.2 鲸鱼优化算法

鲸鱼优化算法是Seyedali Mirjalilia 和Andrew Lewisa 在2016年提出的一种新型群体智能优化算法[13]。在该算法中，群体规模为N 的鲸鱼在空间维度为d 中进行合作觅食，每个鲸鱼有自己专属的位置，为了找到更多小鱼群，它们就需要一种独特的群体合作方式。把第i 条鲸鱼在空间的位置表示为Xi=(Xi1，Xi2，···，XiD)，i=1，2,···，N。每一只参与猎捕的鲸鱼被称为“搜寻代理者”，其所处的最佳位置即可被成为局部最优解[14]。鲸鱼优化算法就是利用具有随机的专属的初始位置的“搜寻代理者”通过泡泡网的捕食策略再找到最多小鱼群的位置，这就是优化位置的全局最优解，其泡泡网捕食习性模型如图2所示。

图2 鲸鱼的泡泡网捕食习性模型

鲸鱼优化算法共包括3种位置更新：包围猎物、旋转搜寻、随机搜寻。

1）包围猎物。该过程中每只鲸鱼都会将目前已经搜寻到的猎物的位置以及猎物的规模大小等信息进行共享，然后鲸鱼会向当前群体中最接近最优猎物的那只鲸鱼进行靠近，该过程会逐渐收缩整个鲸鱼群的包围圈，故称其为包围猎物。该过程的鲸鱼位置更新公式为：

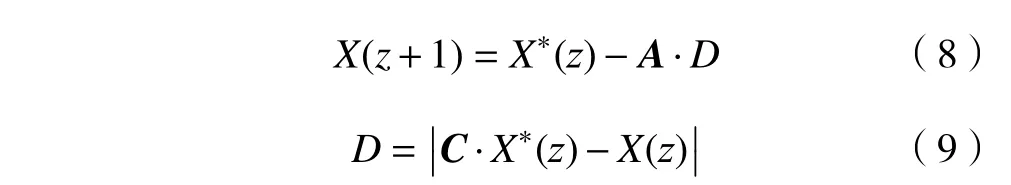
式中：z 为迭代搜寻次数；X 为鲸鱼位置；X*为全局最优位置；A和C 为系数矩阵；D 为鲸鱼与猎物的距离。

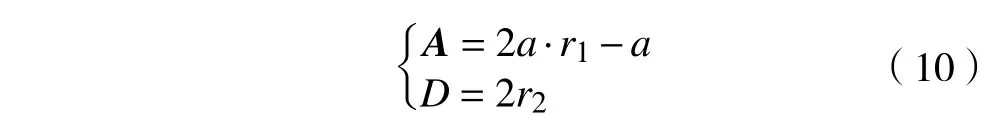
式中：r1和r2为[0,1]均匀分布随机数；a 为收敛因子，从2到0线性递减，a=2-2z/zmax，zmax为最大迭代次数。

2）旋转搜寻。鲸鱼群搜寻猎物是螺旋向上，慢慢靠近目标的方式，其搜寻的位置表达式为

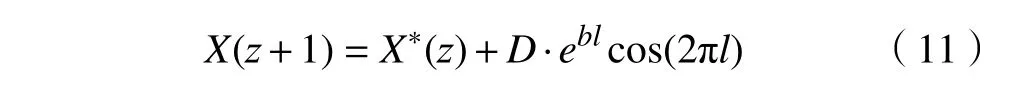
式中： b为常数，可以改变螺旋的形状； l为[-1,1]均匀分布随机数。

鲸鱼在螺旋搜寻猎物过程中，还会顺带收缩包围圈。螺旋位置更新模型如图3所示。

图3 螺旋位置更新模型

为了实现两个动作同时进行，需要用到 p为[0,1]之间的分布随机数。公式需要更新为：

3）随机搜寻。为了提升鲸鱼捕食的全局搜索能力，让鲸鱼在猎物搜寻中具有一定的随机性，同时增加鲸鱼群的搜索范围，所以整个搜索的位置变化过程需要增加随机搜索。

当系数|A|≥1时，说明该鲸鱼在收缩包围圈外，此时选择随机搜索方式；当系数|A|＜1时，说明该鲸鱼在收缩包围圈内，此时选择螺旋包围搜寻方式。随机搜寻更新公式为

式中 Xrand为一个随机的鲸鱼位置。

1.2.3 WOA-VMD模型鲸鱼优化算法在实际应用中的步骤如下：

1）需要确定一个鲸鱼猎捕的目标即适应度函数。每一只鲸鱼每一次的位置更新的结果就是对应该次的适应度函数的值。在该位置迭代中以WOA 作为优化变分模态分解算法的外框架。

2）将优化变分模态分解每次分解得到的K 个IMF分量的峭度值作为内框架，分别把各个IMF分量组的计算得到的峭度值作为WOA 算法的适应度，其中IMF分量对应的最大峭度值称之为局部最大值，表示为 maxLKiIMF，与 maxLKiIMF所对应的IMF分量就是第K 组的所有IMF分量中含有最多故障信息的分量，但这只是局部最优分量。

3）在得到局部最优分量的基础上求解全局最优分量，需要对不同K 和 α计算每一组IMF分量计算maxLKiIMF，最大maxLKiIMF所对应的那组分解IMF的个数K 与惩罚因子α 即是全局最优解。

1.3 CNN模型的构建及参数优化

1.3.1 CNN 模型构建作为一种典型的深度学习方法-CNN[15]，其包括输入层、卷积层、池化层、全连接层、中间层与输出层等，为达到更好的学习与训练效果，往往多个卷积层与池化层交替连接，如图4所示。

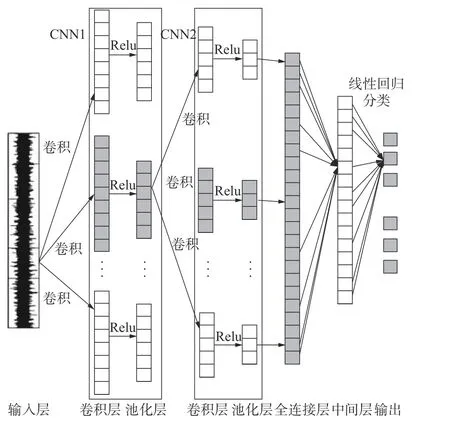
图4 一维CNN 结构模型

1）卷积层。其作用主要是通过卷积核的卷积运算对输入数据进行特征提取。数学表达式为

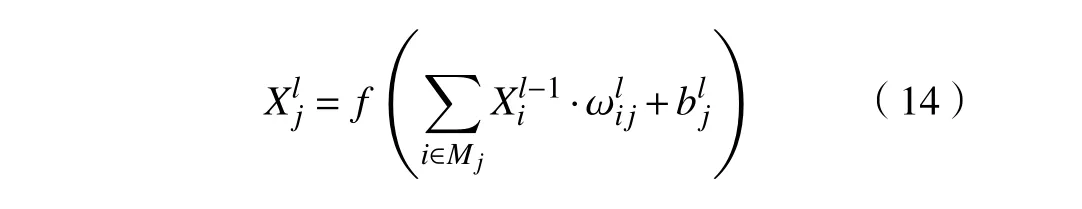
式中： Xlj为第l层第j个元素； Mj为 l-1层特征图的第j个卷积区域； Xil-1为其中的元素； ωlij为对应卷积核的权重矩阵； blj为偏置项； f(·)为激活函数，即Relu函数。

2）池化层。用来对得到的特征图进行降维处理，且在降维过程中能够保持特征的强度。此处采用最大池化（Max pooling）的方法，其数学表达式为

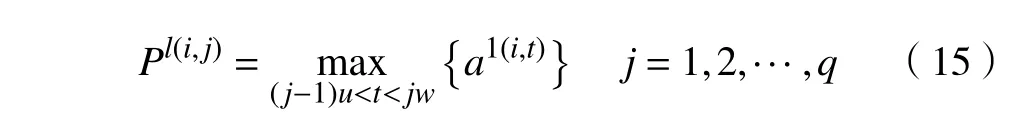
式中： a1(i,t)为第一层的第i个映射图的第t 个神经元；w 为卷积核的宽度。

3）全连接层。其目的是对完成提取的数据根据其特征进行分类，从而实现不同故障类型的识别，数学表达式为

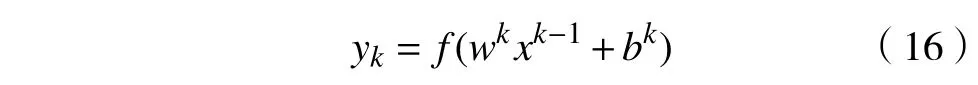
式中： k为网络层的序号； yk为全连接层的输出；xk-1为展开的一维特征向量； wk为权重系数； bk为偏置项。

一维的CNN 模型已经能够广泛应用于机械振动领域。Ince等[16]已经应用一维CNN 对电机进行故障诊断，吴春志等[17]在某坦克变速箱的故障预测与健康管理方面使用CNN 与传统故障诊断方法的对比，结果表明，一维CNN 的故障诊断效果优于传统机器学习方法。

尽管CNN 在故障诊断方面已经取得了良好的效果，但由于CNN 参数多且参数的选择主要依靠经验。如果直接做粒子群算法，容易造成局部最优，单独做正交分解，难以获得较好的优化精度。所以本文首先利用正交试验[18]方法获得一定范围内的最优解，再利用多目标粒子群优化方法[19]（Multi objective particle swarm optimization，MOPSO）获得全局最优解，如图5所示。

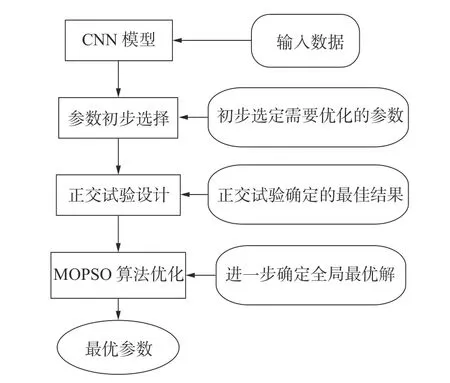
图5 获取CNN 最优参数流程

1.3.2 正交试验设计

使用 Ln(qm11,qm22,···qmii,···,qmrr)来表示正交表，正交实验的个数用n 来表示，实验中的不同水平位置用r 来表示，不同因子i 的水平位置用 qi表示，可以容纳 qi水平因子的个数用 Mi来表示。分析过程如下：

1）计算各个因子i在同一水平下的实验结果y 之和，即

式中 y(Mi(qi)) 表示 Mi因子在 qi水平对应的试验结果。

2）计算各个因子在其同一水平下所有的实验结果y 的平均值

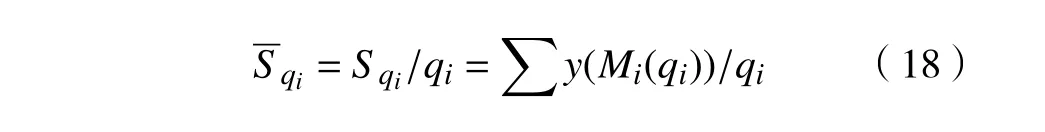
3）进一步讨论各因子对实验结果的影响大小排序，需要通过极差分析实现。极差计算方法为

根据第三步的极差计算后得到各因子对结果影响的排序，同时根据各因子的最大值可以得到最优水平，然后将所有最优结果进行组合得到最佳方案，这就是正交实验方法的最终意义。最后选择用来确定CNN 参数的数据样本，如表1所示。

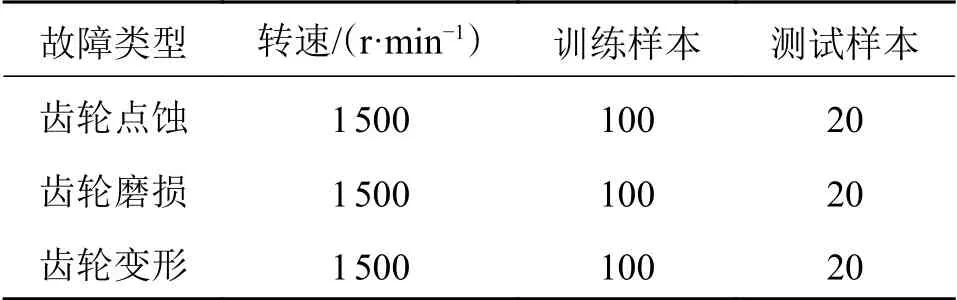
表1 确定参数用数据样本

在进行正交实验中，选择的4个因子分别为：卷积核的个数（A）、卷积核的大小（B）、学习效率（C）和随机失活率（D）。利用正交试验可以使用9组实验数据代替原来需要的81组数据实验，实验结果如表2所示。

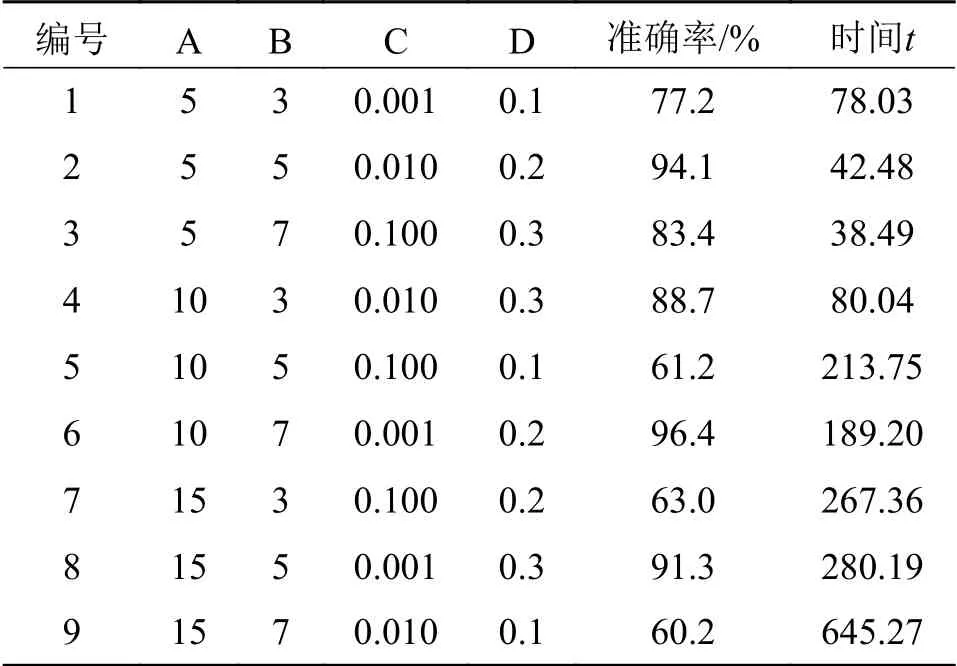
表2 正交实验结果

之后对实验数据进一步分析，E1、E2、E3表示各因子在同一水平下的实验结果之和，e1、e2、e3表示上述和的平均值，Q 表示平均值的极差，具体见表3。

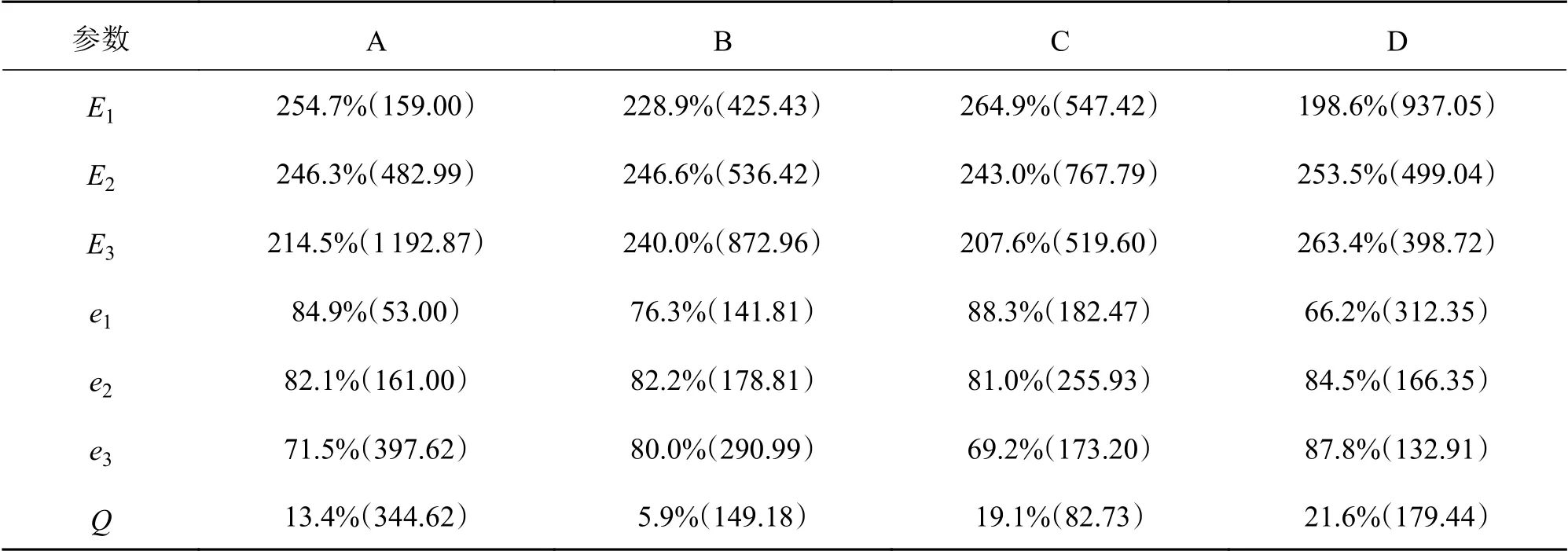
表3 实验数据分析统计结果

对数据进行分析可以确定正交实验法得到的最优的因子组合为A1B2C1D3。

1.3.3 粒子群优化方法

粒子群优化算法以群鸟捕食的策略为原型，每个粒子的位置用来表示每一只鸟在捕食过程中的位置，其第K 次的迭代公式为：

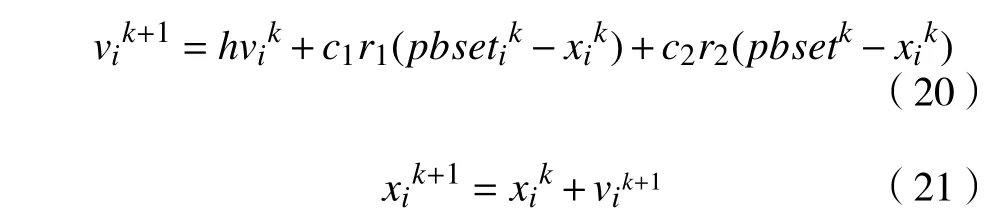
式中： vik、 xik分别为该算法在第K 次迭代得到的速度与位置； pbsetik、 pbsetk分别为在完成K 次迭代后的局部最优解与全局最优解； c1、c2分别为个体所具有的经验与种群所具有的经验；h为惯性权重系数。

相较于传统的基于单目标的优化的PSO算法，MOPSO具有对多目标的优化能力。在优化过程中，算法确定的非劣粒子作为全局领导者，在完成预定的迭代次数后获得该条件下的全局最优解，如图6所示。实际应用过程中，算法的初始化需要根据实验经验与实际状况进行赋值，此处令粒子群容量为100，迭代次数为400，c1和c2分别为1和2，适应度函数由齿轮磨损的故障的诊断成功率与诊断运行的时间共同决定，其变化范围为-100～0，且其绝对值越大，效果越好。待优化的学习效率搜索范围为0.001～0.1，随机失活率搜索范围为0.1～0.4，卷积核的搜索范围为1～10，卷积核个数的搜索范围为1～ 20。

图6 粒子群算法流程图

在使用正交优化算法获得了CNN最优参数的粗略范围的基础上，使用多目标粒子群优化算法进行进一步参数确定，如此既能对多目标粒子群优化算法正确性进行检验，又能获得进一步的最优CNN 参数。确定CNN 参数的粒子群优化算法迭代过程如图7所示。

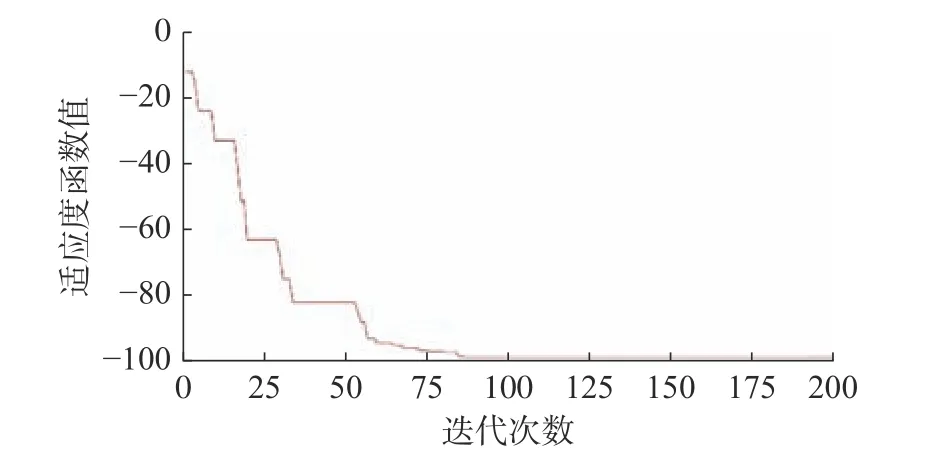
图7 粒子群算法迭代过程图

从图7中可以看出，每一次非劣最优粒子的更新与否都会伴随适应度函数值的改变与否。在迭代次数达到85次左右时，适应度函数值达到稳定，每一个适应度函数值都对应着每一组CNN 参数。

最终得到经过迭代计算后得最优的非劣粒子（卷积核个数为7，卷积核的大小为5，随机失活率为0.13，学习率为0.28），将该粒子对应的数据作为构建CNN 的参数。齿轮箱在齿轮故障中的CNN诊断成功率如表4所示。

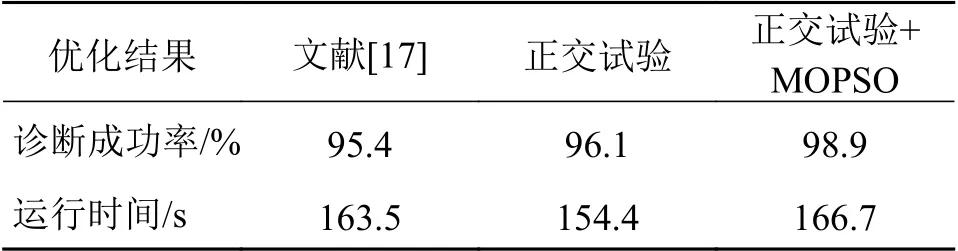
表4 齿轮箱在齿轮故障中的CNN 诊断成功率结果对比

通过在齿轮磨损的故障诊断结果不难看出，正交试验与MOPSO相结合的优化方法在运行时间相差不大的情况下在诊断成功率方面有了明显提高。体现了该优化算法的优越性并为该算法以及该模型在故障诊断方面的推广提供了依据。

2 实例验证

在进行算法的实例检验中，将齿轮箱的故障划分为6大类，6个故障大类分别为：齿轮点蚀故障类型（Z）、齿轮磨损故障类型（V）、齿轮塑性变形故障类型（N）、轴承磨损故障类型（M）、轴承腐蚀故障类型（J）、轴承断裂故障类型（K）。故障类型X1～ X6分别为属于6大故障类型中的未参与训练的未知故障大类。Z1～Z6表示齿轮点蚀故障中的6种不同故障尺寸的故障类型，V1～V6表示齿轮磨损故障中的6种不同故障尺寸的故障类型。ZX1与ZX2表示齿轮点蚀故障中未参与训练的不同故障尺寸的故障类型，VX1与VX2表示齿轮磨损故障中未参与训练的不同故障尺寸的故障类型。在进行振动信号的采集中，通过加速度传感器获取。采样过程中，电机的主轴转速为1500 r/min，采样频率为5120 Hz，采样点数为4096。代表性的列出N1故障下的齿轮箱振动信号的时域图与频域图如图8所示。图8a）中存在明显的振动冲击以及噪声信号；图8b）中存在多个共振带。接下来使用优化的变分模态分解对信号做进一步处理。

图8 N1故障下齿轮箱振动信号的时域和频域图

使用鲸鱼优化算法对分解的参数进行确定，适应度函数为N1故障下信号的峭度值，被优化的参数K 与 α的初始范围分别为1～15与400～ 3200，迭代次数设置为100，K 与 α的迭代步长分别为1与100。峭度值在迭代图中用其相反数进行表示，如图9所示。

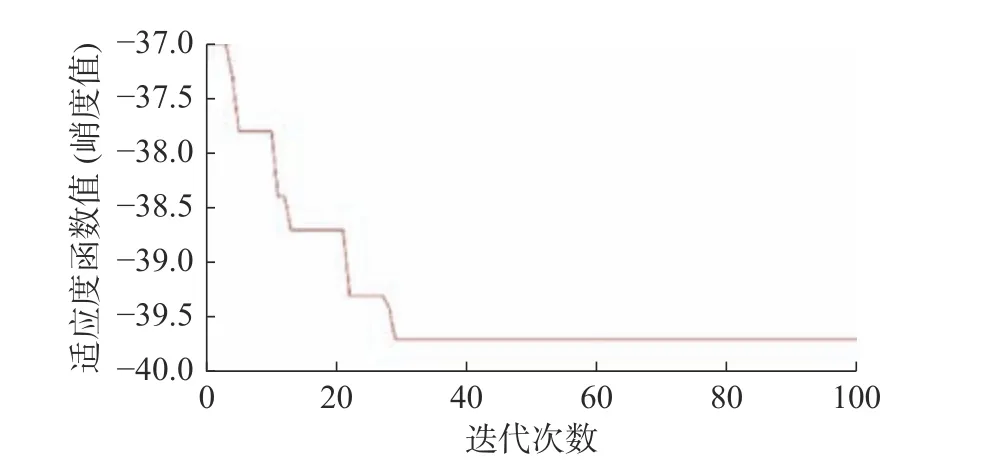
图9 鲸鱼优化算法迭代过程图

从图9中得到的最大峭度值为39.7，充分变现除了此时的齿轮箱正处于较大故障状态。此时输出该峭度值所对应的分解参数K 与α，其中K 为5，α为2800，在此分解参数的基础上完成信号的模态分解，如图10所示。

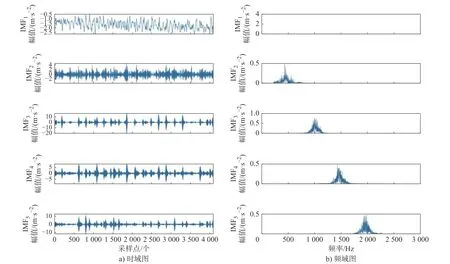
图10 N1故障下齿轮箱振动信号的VMD 分解时域图及频域图

完成模态分解后，分解后也获得了拥有局部最优解以及全局最优解的IMF特征信号。将在该种故障情况下得到的特征信号输入优化的CNN 系统中进行训练。

为了能够得到更加准确全面的故障信息数据，确保诊断的正确率的提高，将分解的IMF分量按照频率的从小到大堆叠为一个多通道样本，之后通过建立的CNN自适应的融合IMF分量的信息并且提取特征，特征类型具体包括谱峭度、峰值指标、峭度指标、频谱能量。每一个故障类型对应的样本训练的故障数据维度从1×M 变为1×M×K，其中M、K 分别为训练或检测样本个数与每个不同故障类型的数据经过VMD分解得到的IMF的个数。将所有故障类型的数据进行上述操作，构建一个完整数据集，进而进行数据的训练与测试。

最后将训练完成的CNN系统先对之前的训练数据诊断齿轮箱故障类型，并根据诊断结果对该深度学习系统的诊断成功率进行定量分析。首先针对每一个故障大类的训练与检测成功率进行分析，每一次的训练样本与检测样本数量为100，结果如图11～图14所示。

图11 训练数据输入结果1（训练结果）

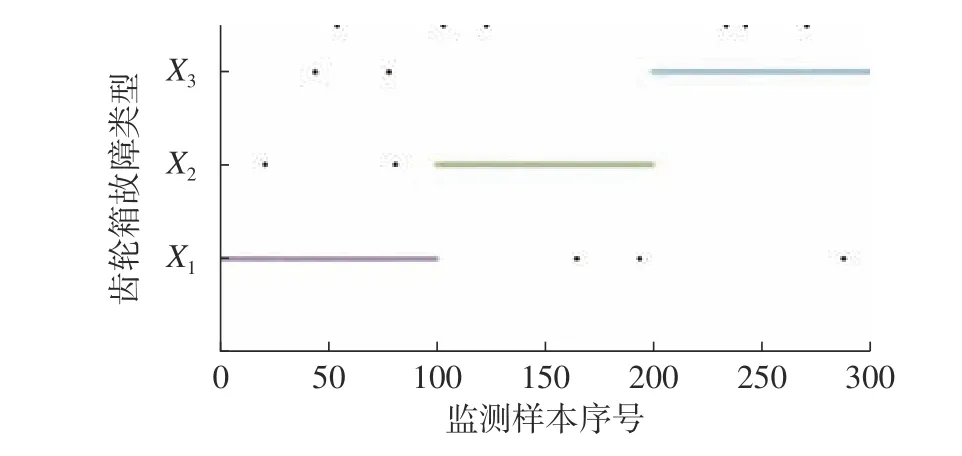
图12 未训练数据输入结果1（检测结果）

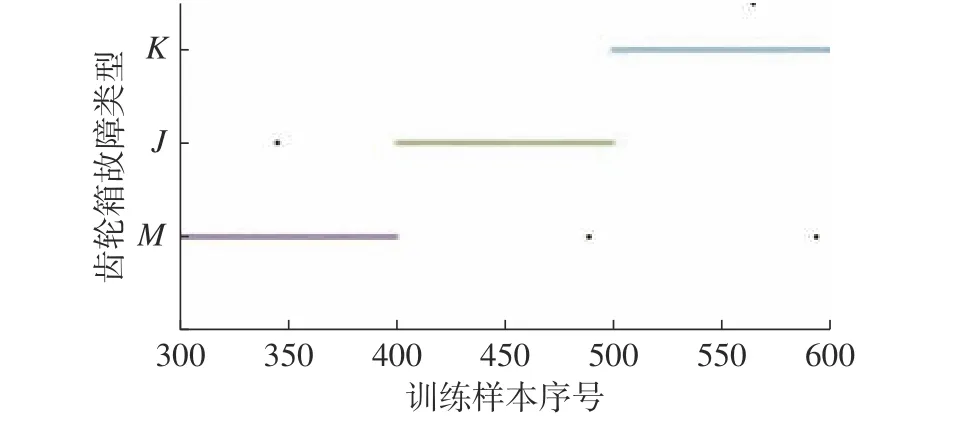
图13 训练数据输入结果2（训练结果）

图14 未训练数据输入结果2（检测结果）

在图11～图14中，训练样本的诊断成功率为98.7%，明显高于检测样本95.7%的诊断成功率，体现了该CNN 模型优秀的故障识别与故障诊断的能力。

实验结果说明该CNN 模型学习训练充分并已经达到了一定的深度，但由于CNN的固有特点，其在检测实测中表现出学习与识别能力仍有提升空间。所以，如果有充分的不同类型的故障数据，该神经网络便会有更深度的学习程度，便会有更好的故障训练与检测效果。

接下来针对故障类型齿轮磨损与齿轮点蚀故障尺寸进行训练检测，获得实际故障尺寸与训练故障尺寸、实际故障尺寸与检测故障尺寸的关系，进而得到CNN 模型的诊断效果如图15和图16所示。

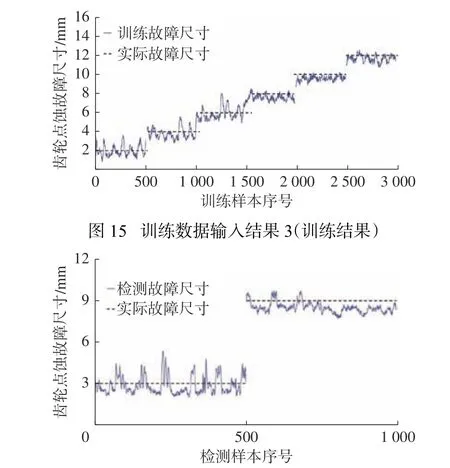
图16 未训练数据输入结果3（检测结果）

此方案中检测的故障尺寸在训练尺寸范围之内。在齿轮点蚀的故障尺寸的训练结果中，训练与检测得到的故障尺寸在实际故障尺寸周围波动。并且在故障尺寸为8 mm 与10 mm 时，实际值与检测值接近程度最高，说明了该尺寸下的学习程度较好。训练与检测的整体效果也能表现出该CNN 模型对训练集达到了充分的学习。

齿轮磨损的故障类型的训练与检测结果如图17和图18所示。

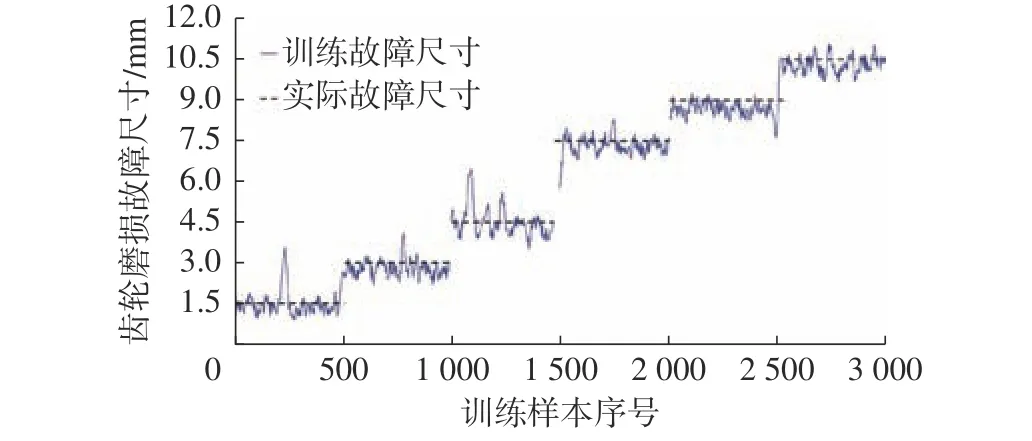
图17 训练数据输入结果4（训练结果）

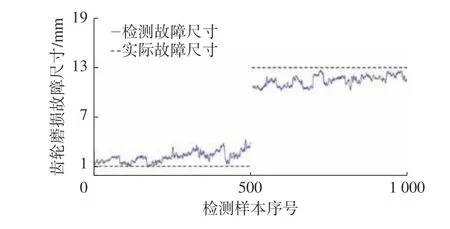
图18 未训练数据输入结果4（检测结果）

在齿轮箱磨损的故障尺寸的检测中，选择的故障尺寸均在训练的故障尺寸之外。从检测结果中也可以发现，低于训练尺寸的检测结果均高于实际值，高于训练尺寸的检测结果均低于实际值，这符合CNN 的学习特点。

最后对实验结果分析如表5和表6所示，其中：A 为文献[17]使用的方法，B 为未使用参数优化的CNN模型诊断方法，C为文中使用的方法。

表5 训练实验结果统计

表6 检测实验结果统计

通过对3种不同方法的训练以及检测结果发现：方法A 在构建CNN 模型过程中，通过对实验数据的诊断效果进而对CNN 模型进行优化，得到的优化模型在诊断效果上得到了提升。但CNN 模型的核心参数并未得到优化，导致该方法具有较差的普适性；B方法使用基本CNN模型进行诊断，并取得一定的诊断效果，说明CNN在故障诊断方面表现出色但仍有提升空间；C方法在使用正交与MOPSO相结合的方法并且在大量实验数据的基础上实现对CNN 模型参数的优化，取得了最好的诊断效果。