自相似仿生层次多胞薄壁管的耐撞性研究及优化
2022-02-13徐少强李伟伟李琳
徐少强,李伟伟*,,李琳
(1.山东理工大学交通与车辆工程学院,山东淄博255000;2.山东理工大学数学与统计学院,山东淄博255000)
据国家统计局的数据显示,截止2019年末全国民用汽车的保有量已经达到了2.541 亿辆,较2018年末增长了2240万辆[1]。伴随着汽车保有量的大量增加,交通安全成为了人们主要关注的问题。合理的优化汽车的防撞结构,不仅可以降低汽车制造的成本,还可以很好的保护车内成员的生命安全。汽车的防撞结构中大部分都是薄壁结构,像汽车的前纵梁、吸能盒、边梁等,它们通过自身的压溃变形来吸收大量的冲击能量,从而缓冲瞬间的冲击力,达到保护车内乘员生命安全的作用[2]。
传统的方形和圆形薄壁结构因其生产成本低,且具有较高的能量吸收效率,被大量应用于吸能结构当中[3]。近些年来,薄壁结构的耐撞性优化一直是国内外科学界和工程界研究的热点。Alexander[4]发现圆形薄壁管的压溃过程是一个轴对称变形模式,提出了圆形薄壁结构在该模式下的平均冲击力计算模型。Wierzbicki和Abramowicz[5]发现Alexander 研究中的管壁弯曲过程是曲线并不是直线,提出了超折叠单元理论,给出了更加准确的平均冲击力计算模型。Chen 等[6]将薄壁结构压溃时折角处用3个三角单元的薄膜变形能和弯曲变形能所替代,简化了超折叠单元理论。Najafi等[7]比较系统的研究了在薄壁结构中添加肋板连接后的耐撞性,推导了多胞情况下平均冲击力的计算公式。Zheng等[8]横向研究了厚度对LVT 多孔管能量吸收的影响,结合仿真结果和实验数据给出了吻合度较高的平均力预测公式。
近年来,将仿生学与结构设计相结合的方法被广泛的应用在各大领域。Zhou 等[9]对竹竿结构进行了研究,提出了仿竹节优化梁的模型,较传统的结构强度提升了80%。许述财等[10]通过观察竹节的结构特征,基于竹结构设计出由仿生节、仿生单元和仿生内管组成的仿生吸能管。
本文通过对樟子松结构的观察,结合当前多胞薄壁管的研究提出了一种新型的自相似多胞薄壁吸能结构,并将不同层次仿生薄壁结构的耐撞性进行了理论分析预测和仿真模拟结果对比,结合响应面法和遗传算法进行了多目标优化,得到了耐撞性较好的薄壁管结构尺寸。
1 仿生层次多胞薄壁结构设计
1.1 仿生原型分析
“物竞天择,适者生存”,不仅仅是自然界生物优胜略汰的自然规律,也用于人类社会的发展。近些年来,植物结构的仿生受到了研究学者们的广泛关注[11]。
基于仿生学的思想,人们开发出了诸多新型截面的结构。本文以樟子松为仿生原型,提出了一种新的自相似层次方管薄壁结构。如图1a)所示,樟子松常用做东北大兴安岭山区及西部砂丘地区的造林树种,图1b)是将其简化后的结构图,可以看做是一种自相似分形结构。从图1c)中可以看出,进行结构的局部放大后,可以发现这些小的子结构都与主体结构是相似的,而樟子松在防风固沙中具有显著的效果,与这些都是密不可分的。因此,选取樟子松为仿生原型,结合这种自相似的概念,本文提出了一种新型的自相似多胞薄壁吸能结构。
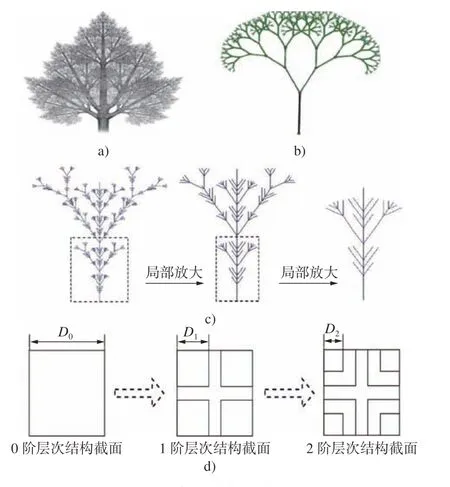
图1 仿生结构的演变
1.2 仿生结构模型
对于该类结构,如图1d)所示,在传统的方管薄壁结构中对其4个角进行自相似的替代重复上述替代过程,就产生了高阶(1阶和2阶)层次多胞结构。考虑到加工难度、成本控制和实际应用的因素,暂时只增加到了2阶层次结构。
在本文中,将传统的方形薄壁结构命名为T0,设计的新型薄壁结构命名为T1和T2,分别对应1阶和2阶层次多胞结构。为了保证结构在压溃过程中的稳定性以及满足加工要求,该薄壁结构各层次结构的尺寸 D0、D1和D2应该满足[12]:

本文初步选取D0、 D1和 D2分别为80 mm、35 mm、20 mm,薄壁结构的管长为200 mm,壁厚为2 mm。
2 有限元模型建立与理论分析
2.1 有限元模型建立
本文通过ANSYS建立了3种薄壁结构的有限元模型,选取AA6060T4铝合金作为薄壁结构的材料,采用LS-DYNA中的123号模型(MAT_MODIFIED_PIECEWISE_LINEAR_PLASTICITY)对这3种薄壁结构进行了轴向压溃的仿真分析[13]。有限元模型参数如表1所示。薄壁结构底端施加固定边界约束,采用恒定速度为10 m/s的刚性墙对结构加载轴向动载荷,冲击压缩距离为管长的75%,如图2所示。

表1 有限元模型参数
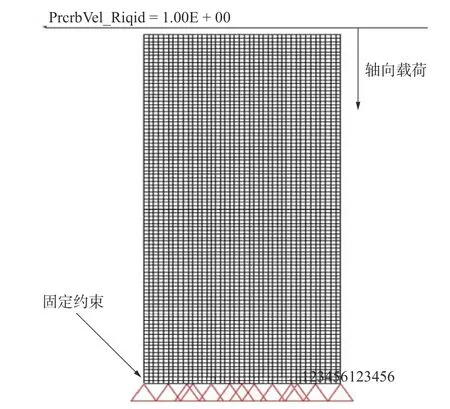
图2 计算模型
薄壁管采用SHELL163中的Belytschko-Tsay壳单元(KEYOPT(1)=12)进行划分,该单元有4个节点,在预防沙漏方面效果显著。在计算过程中,采用了自动单面接触算法来模拟薄壁结构自身产生的接触,其静摩擦因数和动摩擦因数均取为0.2[14],由于单面自接触不输出接触力,在K 文件中添加了关键字力传感器(CONTACT_FORCE_TRANSDUCER_PENALTY)来获取接触力。
2.2 理论分析
对于方型单胞薄壁结构,其在轴向压溃下的平均冲击力通常用超折叠单元理论求得[15],其公式为
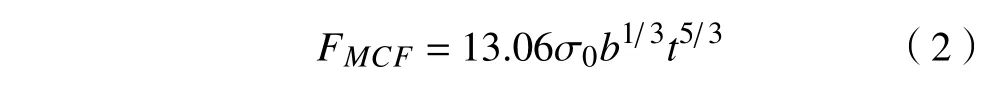
式中: σ0为材料塑性流动应力; b为薄壁管的边长;t为管的壁厚。
对于多胞薄壁结构,通常采用简化超折叠单元理论[6]进行轴向压溃下的平均冲击力预测。
根据简化超折叠单元理论,多胞薄壁管的一个折叠层的压溃过程中,系统的外功等于弯曲变形和薄膜变形的能量耗散之和。
如图3所示,简化超折叠单元是由延展性三角形和静态塑铰线组成的面板单元构成,H 表示一个折叠过程的半波长,实际压溃过程中并不会达到完全折叠的效果,会留出如图3中δ 所示的长度。
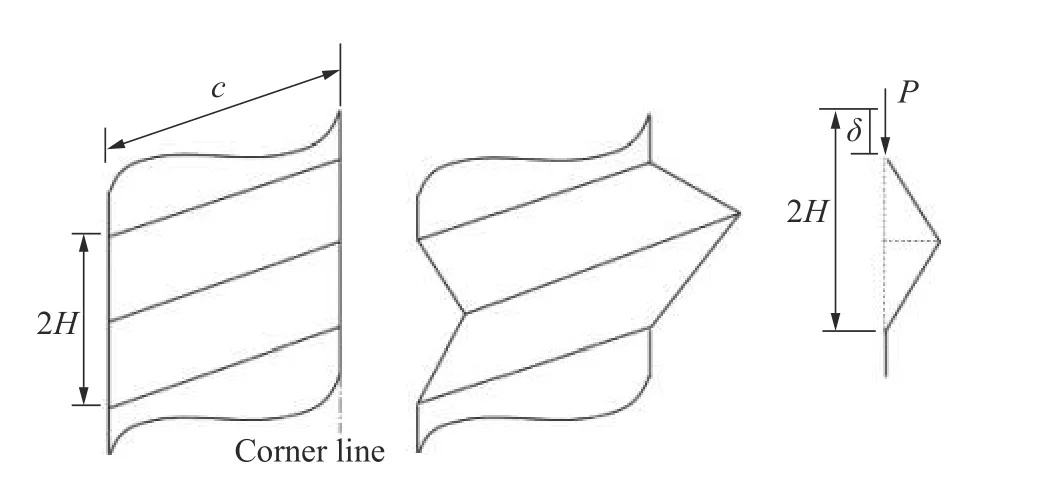
图3 简化的超折叠单元
因此,引入有效压溃系数k 来计算压溃过程中的外功,即
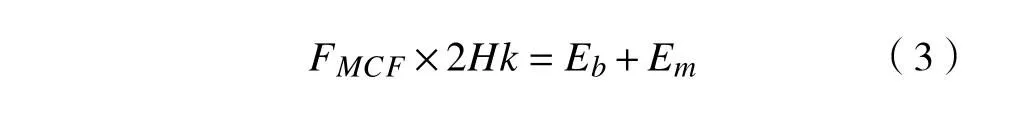
式中: Eb和 Em分别是弯曲变形和薄膜变形的能量耗散。据Wierzbicki等[5]的研究,有效压溃系数k 的范围为0.7~ 0.75,选取k =0.73。
弯曲变形的能量耗散 Eb为
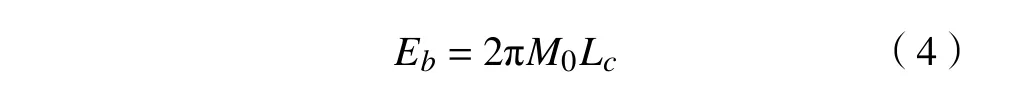
式中: Lc是 截面面板的总长度; M0为折叠单元的塑性弯矩,计算公式为
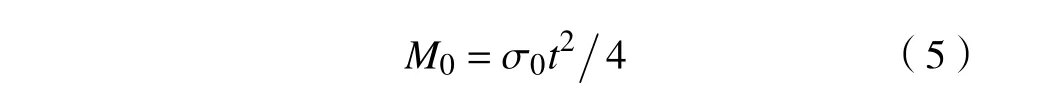
Zhang[16]和Qiu[17]研究了不同角度角单元的薄膜变形能,分别表示为:

如图4所示,新型仿生层次薄壁结构其横截面有直角单元和T形单元组成。

图4 仿生结构截面图
在一个折叠波长2H 内,直角单元的薄膜变形能可以近似表示为
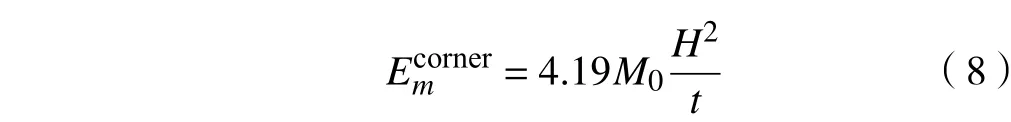
T形单元的薄膜变形能可以近似表示为
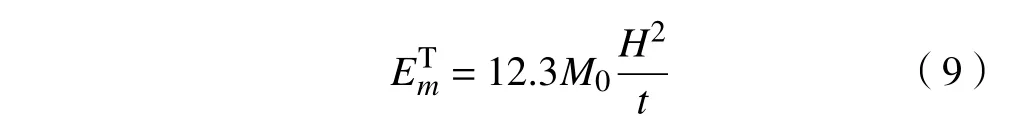
将上述弯曲变形能和薄膜变形能分别代入式(3)中,可得
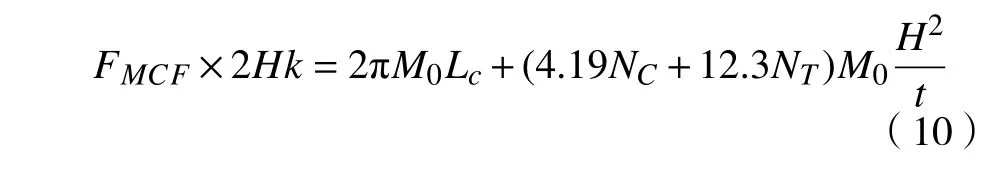
式中: NC、 NT分别对应多胞薄壁结构截面直角及T 形部分的个数。
在折叠压溃的过程中,当管壁在最小的压溃载荷下发生变形时,也是最理想的变形方式,此时,利用稳态条件,即

可得折叠半波长为
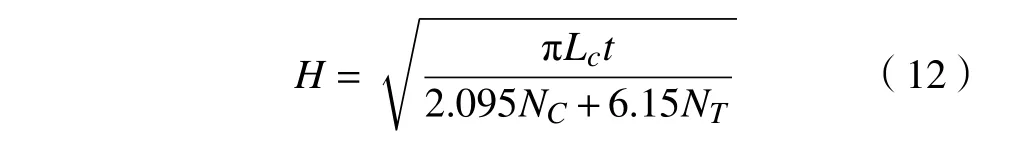
将式(12)代入式(10)中,可得平均冲击力FMCF预测公式为

在本文中,薄壁结构的材料选为铝合金AA6060 T4[18]。需引入动态放大系数λ,对于无缺陷引导的薄壁结构, λ一般取1.3~1.6,本文选取λ=1.3。则公式(13)可修正为

对于T1, NC=8,NT=8,因此平均冲击力为

对于T2, NC=12,NT=16,因此平均冲击力为
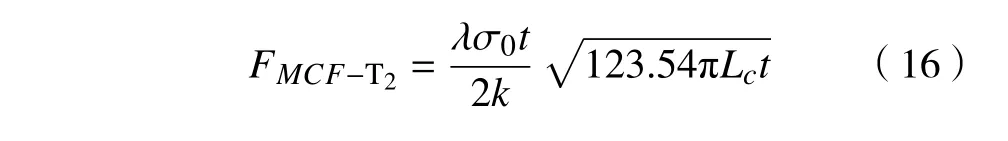
2.3 评价指标
汽车前部的首要吸能装置在发生碰撞时,最理想的状态是在获得较高比吸能的同时,瞬间产生的峰值冲击力也最低,可有效减少该结构向驾驶室传递的冲击力,更好的保护乘员安全。本文选取比吸能、平均冲击力和峰值冲击力作为评价指标[19]。
1)比吸能SEA定义为
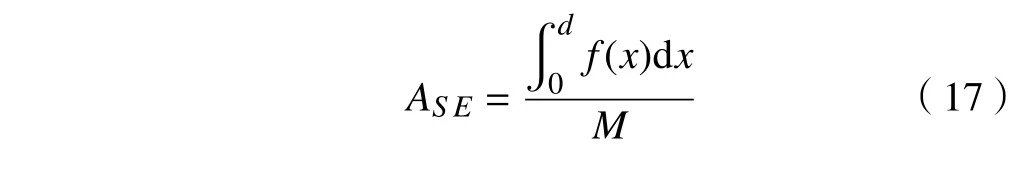
式中: f为碰撞力;M 为试件的总质量;d 为被压缩的距离。
2)平均冲击力FMCF由吸收的能量除以试件被压缩的距离得到,其定义为
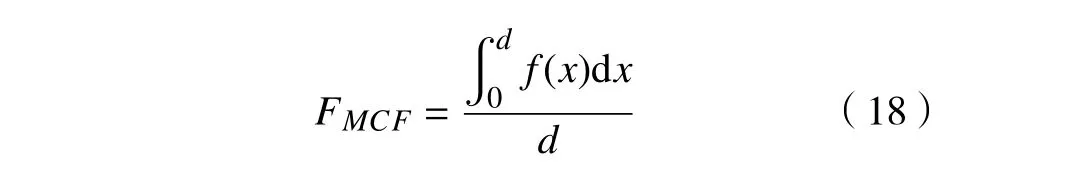
3)峰值冲击力FPCF是指薄壁结构在压溃的过程中的承载极限值。其在碰撞压缩过程中的峰值冲击力应小于设计的许可值,一般控制在200 kN以内,可以避免汽车碰撞过程中变形过程的不稳定性。
3 仿真结果分析
3.1 有效性验证
采用LS-DYNA对上述模型进行计算求解。为保证计算结果的有效性和精确性,需要验证整个压溃过程中的能量守恒问题,必须确保沙漏能控制在总能量的5%以内[20]。
图5给出了各薄壁管在压溃过程中的能量比例曲线(总能量与初始能量之比),可以发现其始终在1附近波动,变化浮动很小,表明整个变形过程中能量是守恒的。
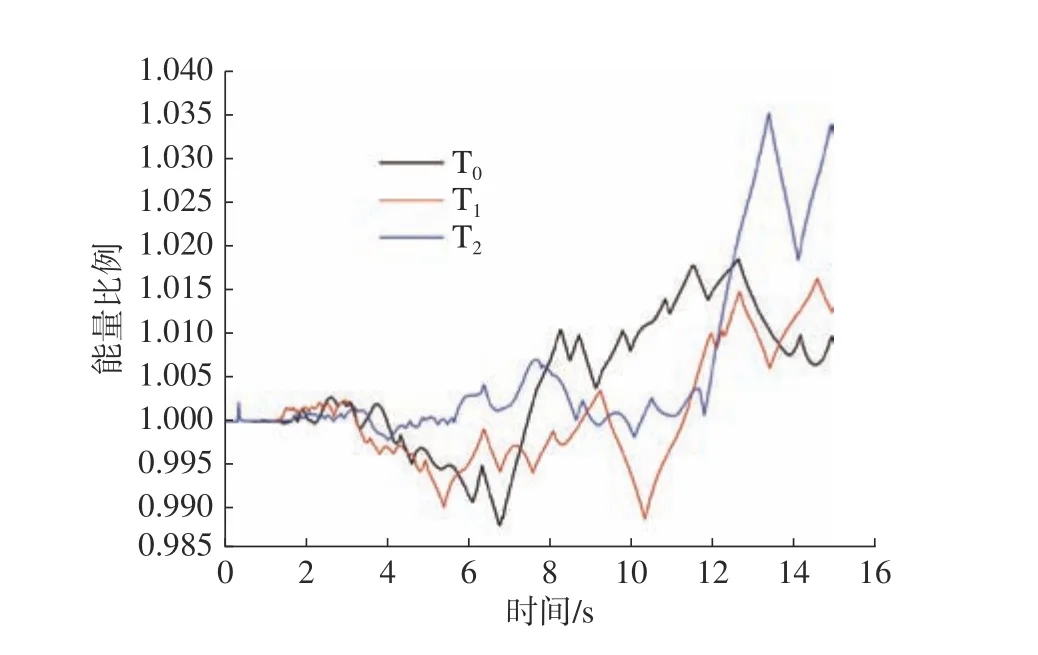
图5 各薄壁管能量比率曲线
各管的沙漏能与质量增加的相应结果如表2所示。由该表可知,各管的沙漏能占内能比例和质量增加百分比均小于1%,符合模型精度要求。因此,沙漏变形得到了很好的抑制,计算结果有效,表明本文建立的有限元仿真模型具有较高的可靠性。
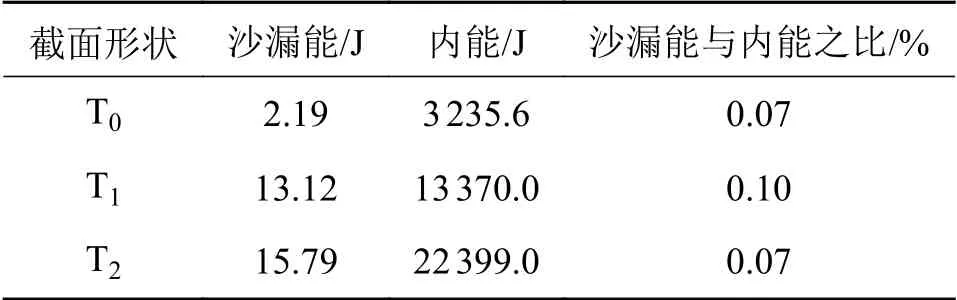
表2 各管的沙漏能
3.2 屈曲变形对比分析
图6显示了3种不同仿生层次结构在轴向压缩下的变形状态。由图6可以看出,3种薄壁结构均为渐进屈曲的变形模式,在压缩距离一定时,相较于传统的方管薄壁结构,新型仿生薄壁结构的褶皱数随着层次结构的增加依次增多,这也意味着其结构的吸能性越好。

图6 3种薄壁结构的变形状态图
表3给出了各薄壁管平均冲撞力的理论预测和数值模拟结果。由表3可以看到,两个结果的相对误差均保持在7%以内,表明平均冲击力的有限元仿真值与理论预测值有较高的一致性,可用于后续的优化研究。
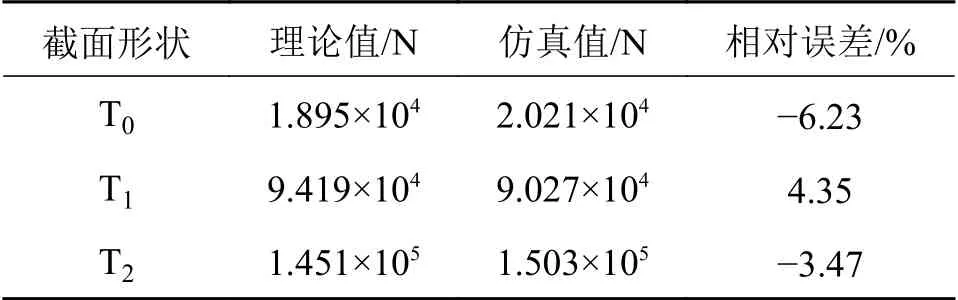
表3 各管冲击力理论预测值与数值模拟值比较
3.3 冲击力对比分析
图7为3种薄壁管冲击过程中的冲击力-位移曲线图。传统的方管结构峰值力为55.742 kN,薄壁管T1的峰值力为141.77 kN,薄壁管T2的峰值力为191.73 kN。从3条曲线的变化趋势可以看出,其波峰、波谷交替出现,对应着不同层次结构模型的逐层压溃,薄壁管T2的波峰波谷交替变化相较于T0和T1稳定许多,其曲线整体保持在较高的水平,说明碰撞过程中,T2吸收的能量较多,吸收效果较好。

图7 各管的轴向冲击力-位移曲线
各管的能量吸收情况如表4所示。由该表可知,在相同壁厚、相同材料的情况下,相较于传统的方管薄壁结构,具有仿生层次的多胞薄壁结构比吸能有了较大的提高。T1和T2的比吸能分别是T0的2.21和2.91 倍。由此可以看出,层次结构的增加能有效提高薄壁管在轴向冲击载荷作用下的能量吸收性能。
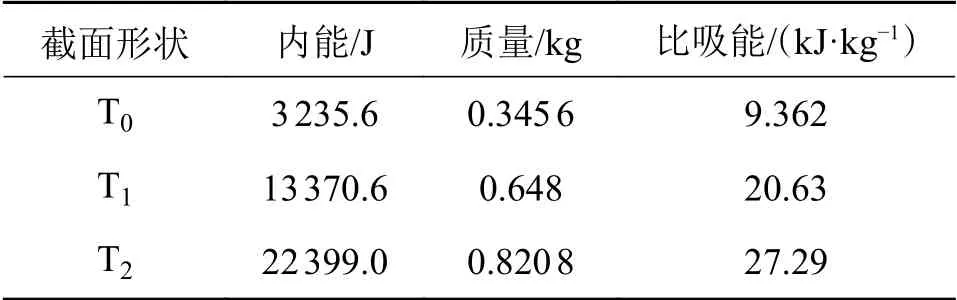
表4 薄壁管的能量吸收
4 仿生结构尺寸优化
通过上述分析可知,薄壁管T2的吸能特性相较于T0和T1要突出很多,因此选取T2作为结构优化的截面。
为了设计制造吸能效果更好的多胞薄壁结构,在优化建模时将吸能盒的峰值碰撞力FPCF和比吸能量S EA作 为优化目标,将薄壁管壁厚t、层次结构尺寸参数 D1以及 D2作为约束,建立的数学优化模型为:

采用拉丁超立方法在空间中选取了20组样本点,并使用LS-DYNA 软件进行了碰撞仿真,表5给出了选取的20组样本点及其计算结果。
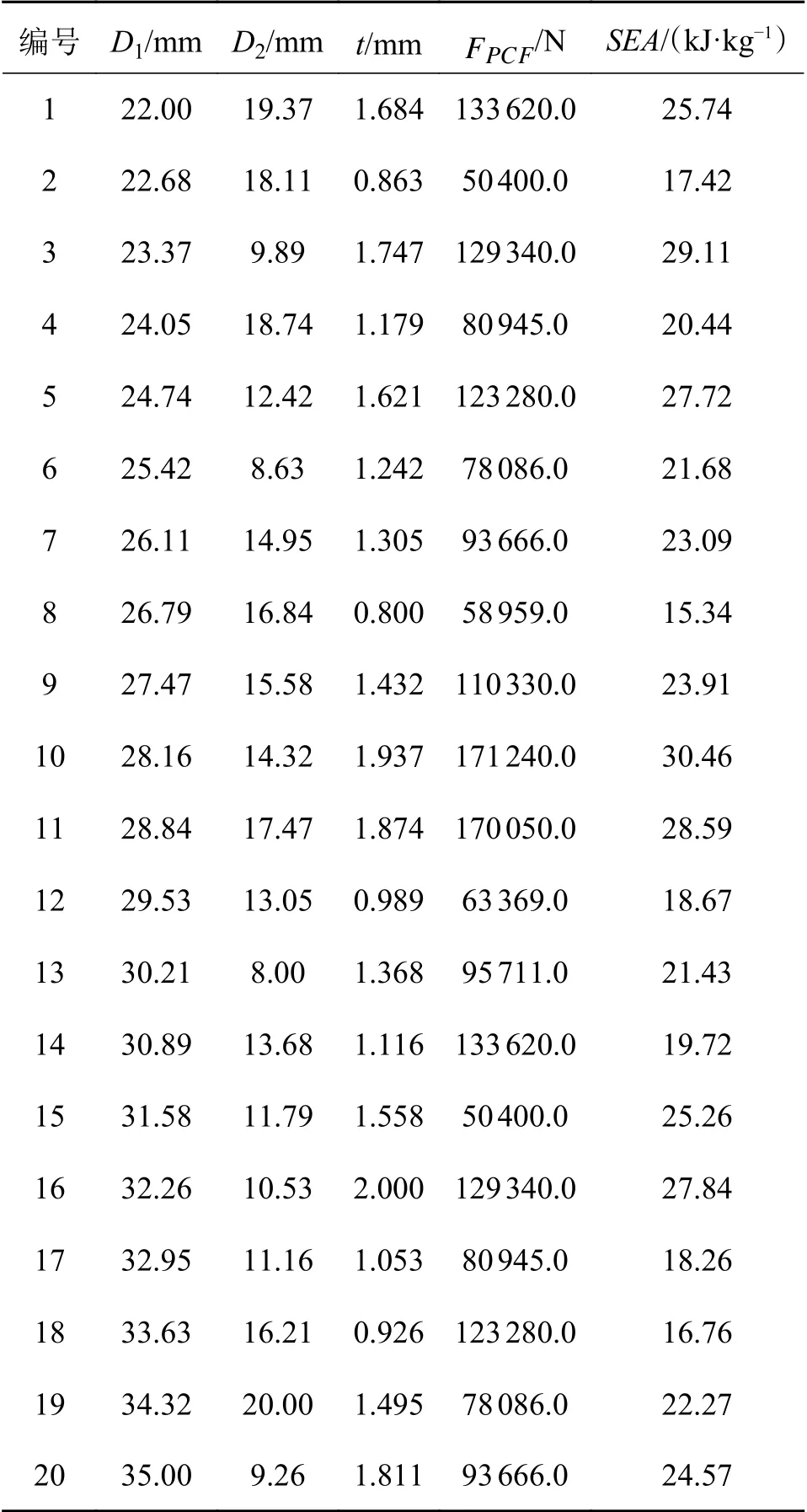
表5 样本数据统计
根据计算结果,本文以层次结构的截面尺寸D1、D2和t为输入变量,峰值碰撞力、比吸能为输出变量,基于径向基函数模型(Radial basis functions,RBF)分别建立了如式(20)和式(21)的二次多项式。

采用统计量确定性系数 R2来评估近似模型的相对误差[21],则
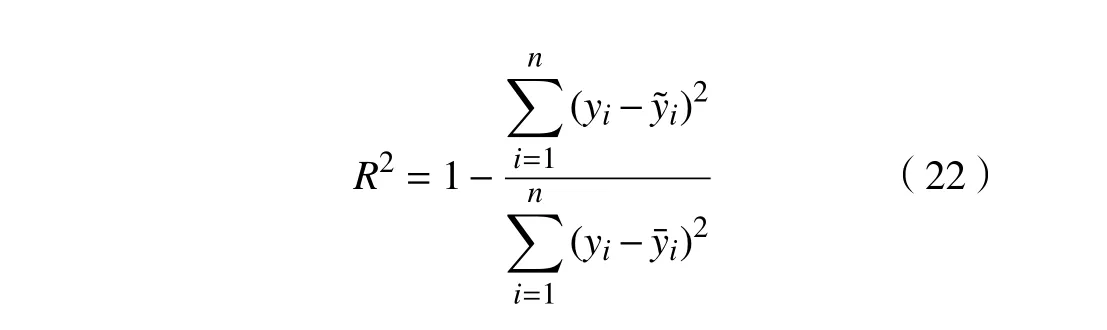
式中:n表示样本点的个数; yi、和分别代表样本点的数值模拟值、理论预测值以及数值模拟值的平均值。
图8a)和图8b)为峰值碰撞力和比吸能响应面模型的误差结果图,其统计量确定性系数 R2分别为0.9902和0.9511,都大于0.9并接近与1,因此,该模型具有较高的精度,为优化设计提供了可靠的基础。
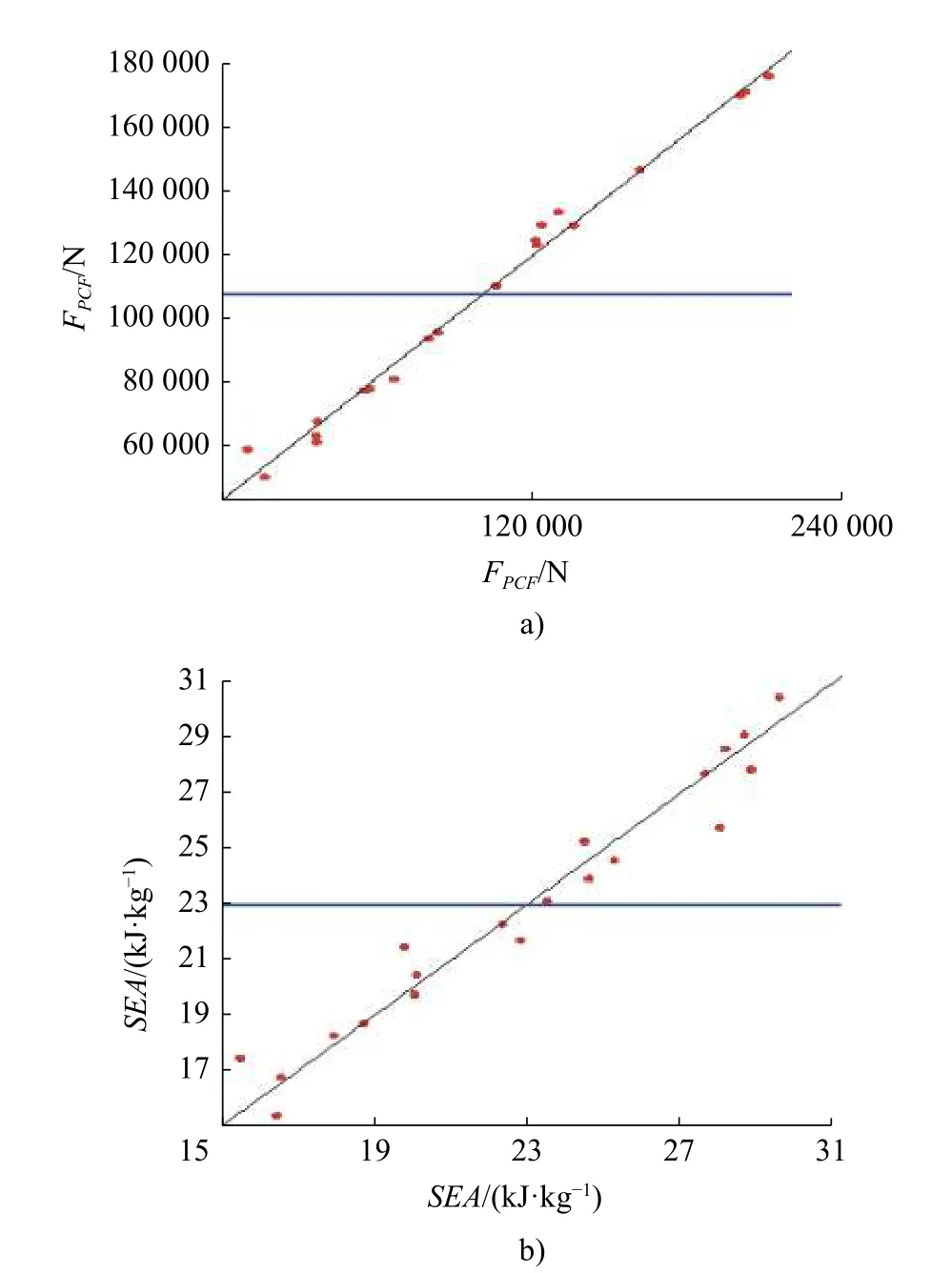
图8 误差分析图
以峰值碰撞力及比吸能为输出变量,在Isight软件中Optimization 模块建立优化流程,如图9 所示。采用了改进的非支配排序遗传算法(NSGA-Ⅱ),种群大小为12,遗传次数为20,经过483次计算后收敛,生成了64组最优解,其最优解集分布的情况以及拟合得出的Pareto前沿如图10所示。
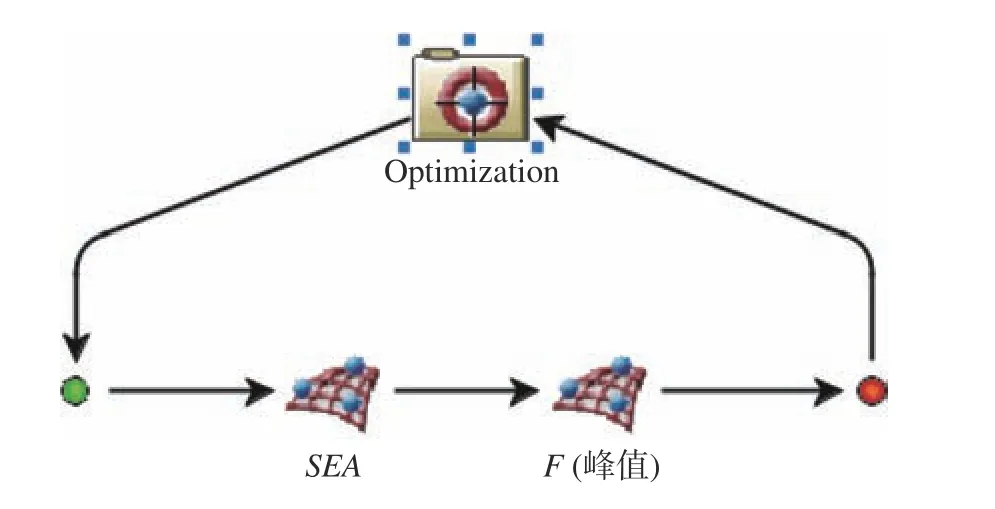
图9 Isight 流程图
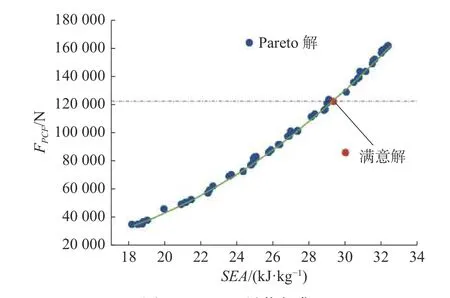
图10 Pareto最优解集
从图10可以看出,峰值碰撞力的变化趋势与比吸能的变化趋势是相互矛盾的,若追求较低单位峰值碰撞力,必然会引起比吸能的下降,两者不会同时达到最优解。实际上,Pareto前沿上的任何一个解都是一个最优解,需要结合工程实际问题进行两者权重的分配。本文选取峰值碰撞力冲击力不大于124 kN 作为设计条件,因此,选取的满意解如图10中箭头所示。
根据该最优解对应的结构参数建立了有限元仿真模型,并将仿真结果与上述建立的多项式响应面模型结果进行了对比,如表6所示,其误差均保持在1%以内,表明响应面优化方法精度较高。
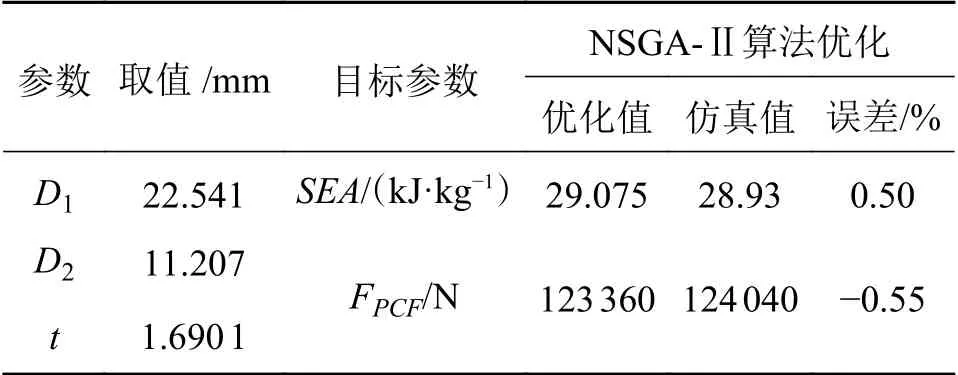
表6 响应面优化值与有限元仿真结果对比分析
5 结论
本文以樟子松的结构自相似性为灵感,提出了一种自相似仿生层次多胞薄壁结构,利用超折叠单元法对该结构进行了轴向冲击下的力学性能理论分析;通过对不同截面结构的有限元模拟结果分析,验证了该理论研究的有效性;最后基于数值模拟结果构建了RBF响应面模型并进行了多目标优化设计。主要结论如下:
1)不同截面对仿生薄壁结构的耐撞性有重要的影响,随着层次结构的增加,薄壁结构的褶皱数依次增加,表明层次结构的吸能效率和变形稳定性得到了较大的提高。
2)基于超折叠单元法推导了多胞薄壁结构的平均冲击力理论模型,并对其进行了预测,与有限元模拟结果吻合度较高。
3)为了得到薄壁结构的最优设计,对耐撞性较好的薄壁管T2使用RBF 模型和NSGA-Ⅱ算法进行了多目标优化设计,得到了T2的Pareto前沿,仿真结果的相对误差均在1%以内。可以根据工程实际问题需要,选择不同的结构尺寸,从而有效的提高薄壁结构的耐撞性。
