一种足式移动机器人的混合视觉伺服控制方法
2022-02-13张德伟刘海涛王仙业肖聚亮
张德伟,刘海涛,王仙业,肖聚亮
(天津大学机构理论与装备设计教育部重点实验室,天津300354)
移动机器人具有更大的操作空间和更高的灵活性,被广泛的应用在各种场合。但由于Brockett 条件[1]的限制,移动机器人通常需要借助额外的状态信息来解决因自身非完整约束而导致的控制系统渐进稳定性和反馈稳定性问题。利用视觉传感器的视觉伺服控制技术具备获取信息全面、可靠性高等优点,能够有效提高移动机器人在非结构环境中的作业灵活度和智能化水平,并提供额外的状态信息构建移动机器人的反馈控制系统,因此近年来得到了快速的发展[2-5]。
视觉伺服控制系统根据视觉反馈信息的类型大致可分为:基于位置的视觉伺服PBVS(Positionbased visual servoing)和基于图像的视觉伺服IBVS(Image-based visual servoing)[6]。PBVS控制方法需要在三维空间中设计控制器,并根据目标对象的图像特征估计相机自身的三维空间姿态。而IBVS方法直接基于目标的图像特征设计控制器,无需三维重建的过程。此外,亦可将两种方法进行组合,从而构建混合视觉伺服方案[7],利用视觉传感器捕获的图像信息构造反映机器人实际位姿的状态变量,作为反馈信息,实现机器人的视觉伺服控制。基于上述3种方法,众多研究者对轮式机器人的视觉伺服控制开展了大量的研究工作。Shi等[8]采用模糊算法提高了图像特征检测的精度,并通过使用两个独立的伺服增益解耦机器人运动的平移和旋转,提高了IBVS控制系统的性能。基于IBVS方法,Ke等[9]设计了一种管道型模型预测控制器使机器人可以更准确地到达指定位置。MacKunis等[10]根据参考图像中目标点与实时图像中对应点的投影几何关系提出一种混合视觉伺服控制方法,实现了轮式移动机器人的跟踪控制。Zhang 等[11]提出了一种基于投影单应性技术的方法用于估计相机的内部参数,并设计自适应控制器解决了轮式移动机器人在输入饱和情况下的轨迹跟踪和调节问题。曹雨等[12]通过利用单应性的转递特性计算单应性矩阵,缓解相机视野约束对机器人运动的影响。李宝全等[13]通过单应性矩阵的快速分解得到了轨迹跟踪误差,并设计自适应控制律,实现了机器人的视觉伺服轨迹跟踪控制。
上述视觉伺服控制方法的研究主要集中于轮式移动机器人,关于视觉伺服用于足式移动机器人的研究较少。相较于轮式移动机器人,足式移动机器人具备更优秀的地形适应能力,在崎岖路面、多障碍物路面拥有更高的通过率。引入视觉控制技术,使足式移动机器人能够获取更丰富的环境信息,具备对跟踪目标的能力,提高足式移动机器人在非结构化环境中的智能型和自主决策能力。然而,足式移动机器人足式机构的运动形式较为复杂,周期性的步态运动易对视觉伺服控制精度造成不利影响。因此,足式移动机器人的视觉伺服控制方法仍有待深入研究。
在先前的工作中,提出了一种新型足式机构,并设计了用于地形探索的八足移动机器人[14]。视觉伺服控制技术是实现该目标的基础,本文提出一种基于单应性矩阵的视觉伺服控制方案,在缺乏目标深度信息的情况下利用视觉反馈实现足式移动机器人的控制目标,并引入足式机构运动学,提高控制系统对机器人的控制精度。通过分析机器人行走机构运动学,建立实现该机器人视觉伺服控制所需的速度映射模型;在机构运动学分析结果的基础上,提出一种改进型自适应中值滤波器,以减小机构的周期运动对视觉反馈过程的影响;基于机器人位姿误差模型,设计滑模控制器,完成视觉伺服控制系统闭环。最后,利用四自由度移动平台和搭建系统仿真实验平台,分别验证了自适应滤波器和控制方法的有效性。
1 系统建模
为实现足式机器人的视觉伺服控制,本节首先建立机器人运动学模型,获得机器人移动速度与机构输入速度的映射关系;通过构建机器人位姿与期望位姿的映射关系,推导用于控制器设计的位姿误差模型,并利用单应性矩阵实现对机器人位姿的估计,完成伺服控制系统视觉反馈。
1.1 机器人运动学分析
足式移动机器人的三维模型如图1所示,该机器人的两组四足行走机构关于平面w1对称布置。每组机构包含两个双足单元,且由同一个电机-圆柱齿轮传动系统驱动。双足单元中两腿的机构共用同一个机架,且机构曲柄相位差配置为π。

图1 足式移动机器人三维模型
当四足行走机构在水平路面行进时,双足单元的两腿依次轮换完成支撑推进和迈步跨越动作,使四足单元产生相对地面的移动速度vLMR。考虑到机器人整体结构的对称性,通过控制两侧四足行走机构的驱动电机转速即可调整vLMR,进而实现对足式移动机器人的运动控制,即机器人运动形式为差速驱动。
为获得机器人速度映射关系,建立的连体坐标系如图2所示Kr。
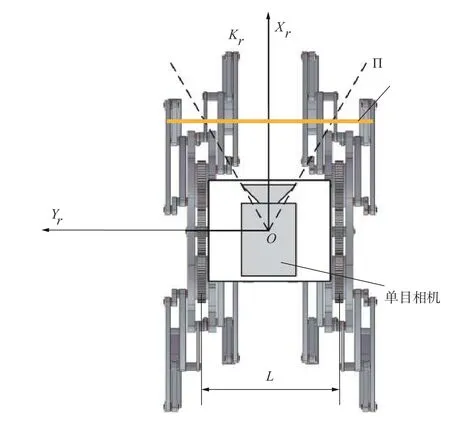
图2 机器人连体坐标系
将单目相机固定在机器人上,并令相机坐标系与Kr系 重合,则机器人机架参考点O的速度与两侧四足行走机构输出速度的映射关系可表示为:
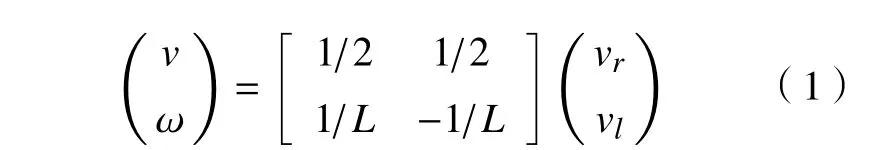
式中:L为 两侧四足行走机构的中心距;v和 ω分别为点O线速度和机器人的角速度;vr(vl)为机器人左(右)侧四足行走机构的输出速度vLMR。
四足行走机构的输出速度vLMR是由电机-齿轮传动系统驱动四腿同时运动形成的,为准确控制机器人移动速度,需进一步分析四足行走机构的运动学,建立机器人速度v和 ω与驱动电机输出转速的映射关系。考虑到机器人八只腿的机构相同,分析四足行走机构的运动需首先完成单腿的机构运动学分析。
机器人的单腿为1自由度平面六杆机构(见图3),由曲柄(杆1)、摇杆(杆3)、机架(杆4)、连杆(杆2和杆5)和输出杆(杆6)组成。

图3 六杆机构示意图
点RA~RF表示各转动副中心, φ表示曲柄输入角度。为建立机构的运动学模型,在点RA处建立参考坐标系o-xy。借助阿苏尔杆组法,可将点RC、 点RF及末端运动输出点RG在o-xy系下的位置矢量表示为:
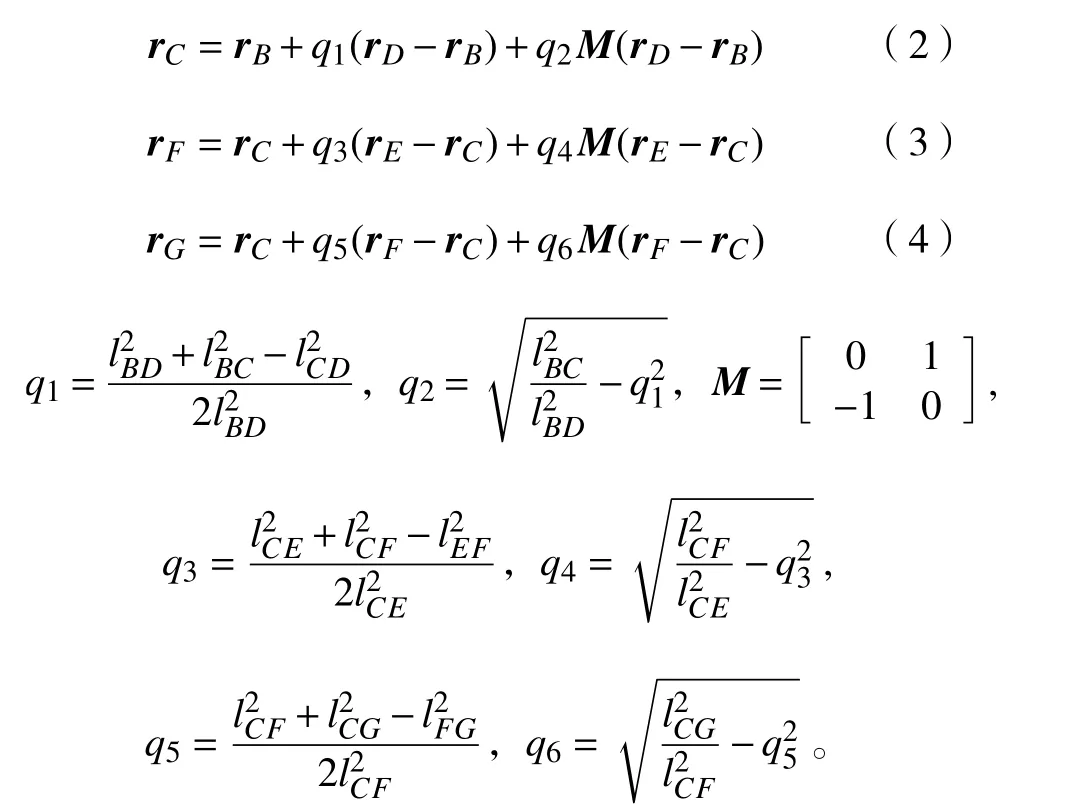
式中:rB、rD和rE分别为点RB、点RD和点RE在o-xy系下的位置矢量;lBC、lCD和lEF分别为杆2、杆3和杆5的长度;lBD、lCE、lCF、lCG和lFG分别为其下标所对应两点之间的距离。
将式(2)与式(3)代入式(4)可得

式中:A=(1-q1-q3q5+q1q3q5)I+(-q2-q4q5-q3q6+q1q4q5+q1q3q6+q2q3q5)M+(-q4q6+q1q4q6+q2q4q5+q2q3q6)M2+(q2q4q6)M3;
B=q3q5I+(q4q5+q3q6)M+q4q6M2;
C=(q1-q1q3q5)I+(q2-q1q4q5-q1q3q6-q2q3q5)M-(q1q4q6+q2q4q5+q2q3q6)M2-(q2q4q6)M3。
注意到: rB=(lABcosφ lABsinφ)T,lAB=‖rB‖, rE=(lAEcosφ lAEsinφ)T,lAE=‖rE‖,故可将式(5)改写为
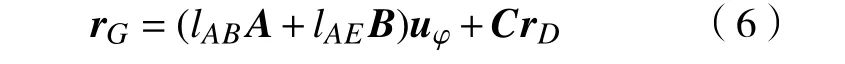
式中:uφ=(cosφ sinφ)T;rD=(lAD0)T,lAD=‖rD‖。
当给定输入角 φ时,利用式(6)可求得机构末端点 RG的坐标。图4示出了当 φ=0 ~2π时,点 RG的运动轨迹(各杆件长度取值见表1)。
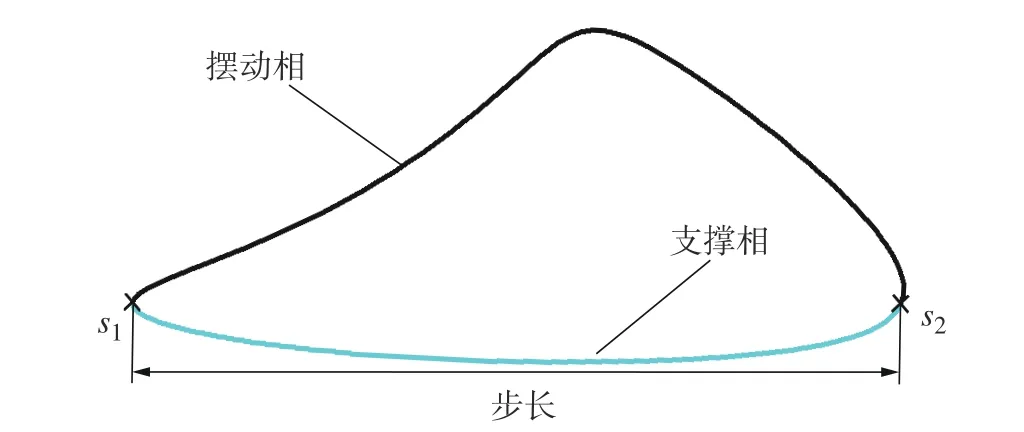
图4 点RG 的运动轨迹

表1 六杆机构无量纲尺度参数
因双足单元由同一电机驱动且单腿机构相同,当机构尺度参数确定后,机构末端点运动轨迹具有唯一性,故双足单元空转时,两腿末端点的运动轨迹相同。假设空转过程中双足单元机架平面保持水平,即支撑相与摆动相的两个切换点位于同一水平高度,由于双足单元的曲柄相位差为π,故可确定在点 RG运动轨迹中的两个切换点 s1和s2,如图4所示。据此,结合式(6)可将双足单元末端点在支撑相的运动轨迹表示为:

式中: φ1( φ2)对应末端点 RG位于 s1(s2)时的输入角度。当取表1所示的机构尺度参数时,经计算可得φ1=75°, φ2=255°。
双足单元在水平路面行走时,其相对路面的运动取决于末端点在支撑相的运动。取点 RA作为机架参考点,结合式(7)可计算出双足单元行走时,当φ=φ1~φ2,点 RA的运动轨迹如图5所示。由图5可知,双足单元沿水平面的行进运动除了具有平行于地面的运动外,还包含一个垂直于地面的周期运动。

图5 点RA的运动轨迹
考虑到四足行走机构的两个双足单元关于平面w2前后对阵布置(见图1b)),若忽略末端点支撑相轨迹不对称部分对四足行走机构运动的影响,四足行走机构的输出速度vLMR与双足单元沿平行于地面方向的运动速度相等。˙迭代计算流程如图6所示。
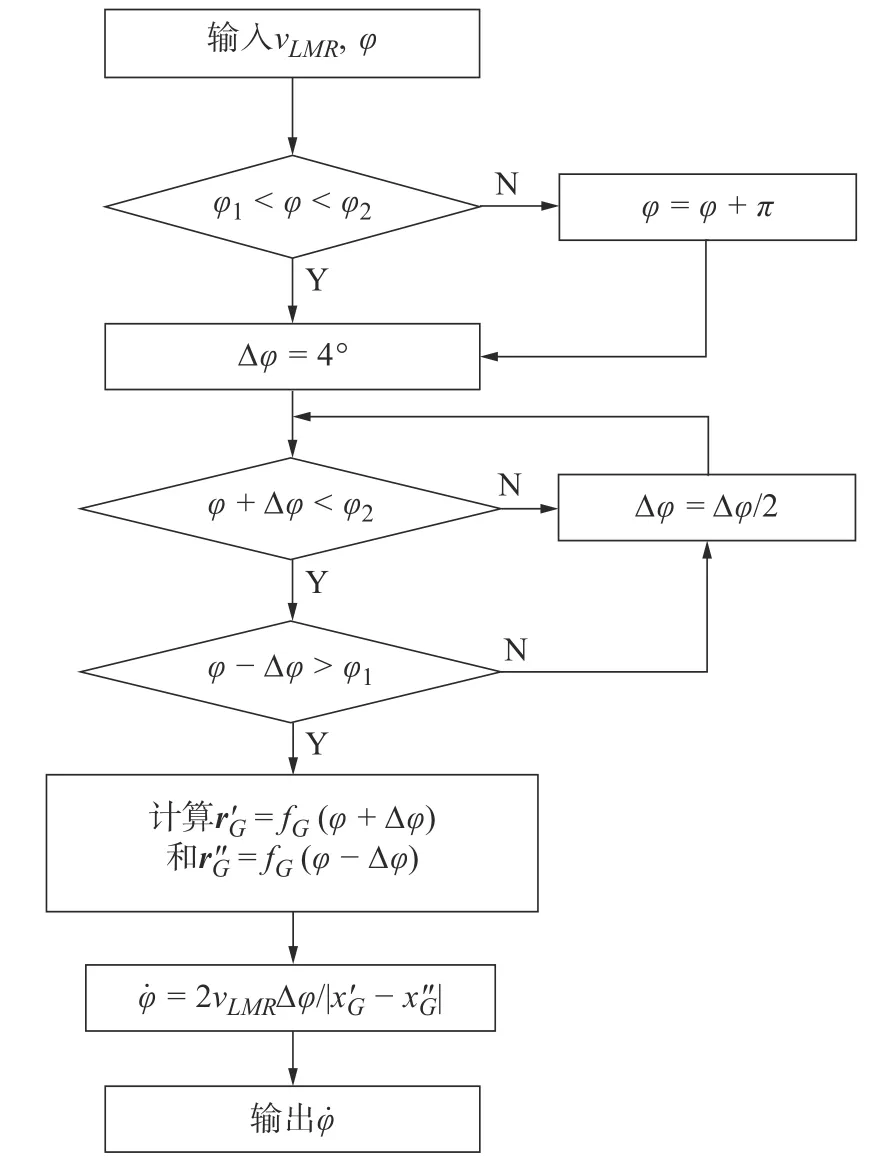
图6 迭代计算流程
为提高计算效率,采用如图6所示的迭代算法建立机构输入角速度 φ˙和四足行走机构的输出速度vLMR的映射关系,并将其简记为

由式(1)和式(8)可建立机器人速度v 和 ω与两侧四足行走机构输入角速度的映射关系为:
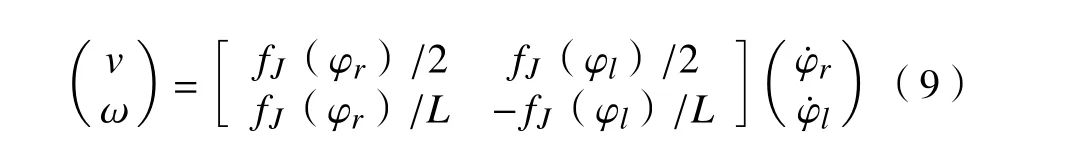
因此,通过分析四足行走机构运动学,可建立机器人线速度和角速度与两侧驱动电机输出转速的映射关系,进而实现对机器人移动速度的准确控制。
1.2 位姿误差模型
本节以机器人在期望位姿处的连体系为局部参考坐标系,描述机器人在移动过程中的位姿变化,并构造用于后续控制器设计的位姿误差模型。
移动过程中,机器人当前位姿与期望位姿的几何关系如图7所示, K为当前位姿处机器人的连体坐标系, K*为期望位姿处机器人的连体坐标系;Πobj为目标点 Pi(i=1,2,···,N )所在平面;n*为平面Πobj的法向量(在 K*系中度量); d*为 K*系原点 O*与平面Πobj的距离。

图7 坐标系关系
由图7可知,K*系相对K系的姿态矩阵和位置
矢量可表示为:
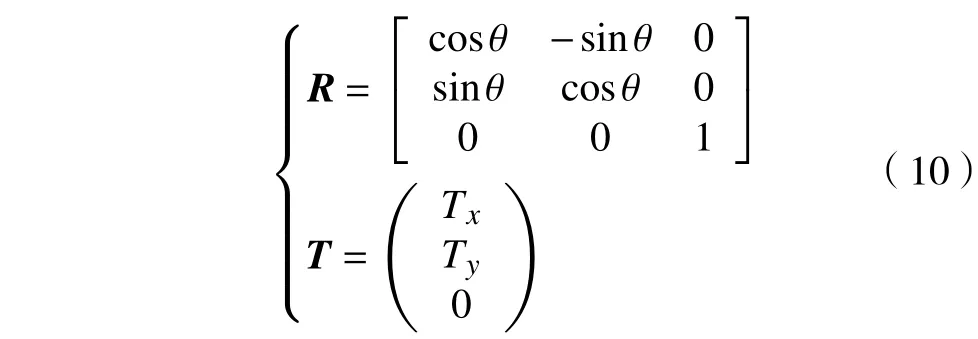
式中θ为 K*系相对 K系的姿态角。
由图7可知,点 O在K*系中的位置矢量为
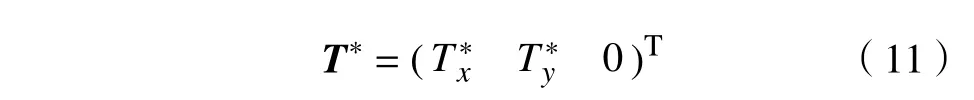
结合 K*系与 K系之间转角的定义,可进一步将机器人移动过程中的位姿记为
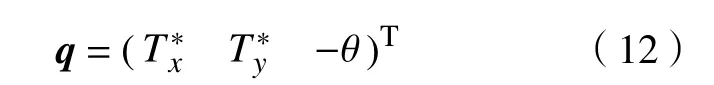
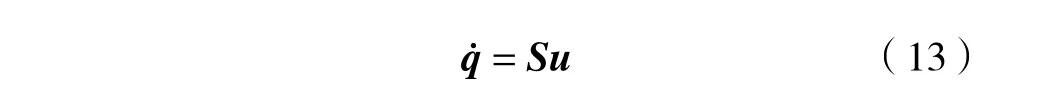

式中: ξ1、 ξ2和ξ3为 位姿误差ξ 的分量。
对式(14)两端求导,并结合式(13)整理可得:

综上,由式(12)、式(14)和式(15)可知,通过调整机器人的线速度和角速度,使位姿误差趋于零,从而控制足式移动机器人逼近期望位姿。
1.3 单应性矩阵的计算与分解
为获得机器人位姿误差ξ,首先需要获取机器人当前位姿 q。本文利用单应性矩阵中的元素构造状态变量,实现对当前位姿 q的估计。单应性是指对一组共面点在不同位姿下拍摄得到的图像间所具有的几何转换关系,而表示其转换关系的矩阵即为单应性矩阵[16]。对于图7中一组共面的目标点 Pi,其在单目相机成像平面内对应像点的像素坐标 pi,可采用SURF、ORB等[17-18]成熟算法识别和提取。将机器人处于期望位姿时由单目相机捕获的图像作为参考图像,令 p*i表示目标点 Pi在参考图像中对应像点的像素坐标,由图像单应性原理[3-4]可知, pi与 p*i的映射关系为
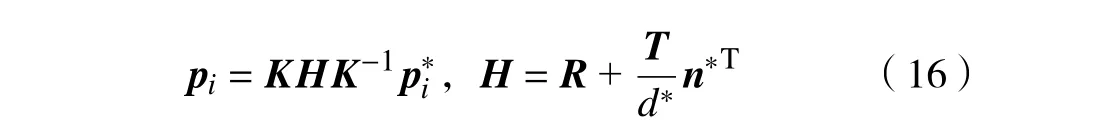
式中: H 为单应性矩阵; K为相机的内部参数矩阵。
假设机器人期望位姿固定,且令 X*轴垂直于平面 Πobj,即n*=(1 0 0)T,由式(10)和式(16)可得到单应性矩阵 H的表达式:
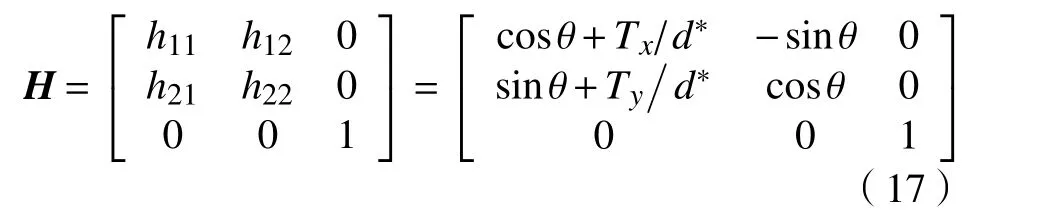
根据式(17)可建立如下等式约束:

此外, T 与 T*的关联关系为[16]

利用式(18)和式(19),可得到机器人相对 K*系的位姿矢量 q,进而结合式(15),即可计算出位姿误差ξ,实现基于单应性矩阵的机器人位姿信息反馈。
2 改进型自适应中值滤波器
由机器人运动学分析可知,四足行走机构沿水平面移动时,除了具有平行于水平面的运动外,还包含一个垂直于水平面的周期运动。该运动会使单目相机捕获的图像出现偏移和旋转,直接对单应性矩阵的计算产生有界干扰,进而影响位姿误差解算的准确性。结合机器人运动学分析结果,本节提出一种改进型自适应中值滤波器,以减小该周期运动对机器人位姿估计过程的影响,滤波计算流程如图8 所示。
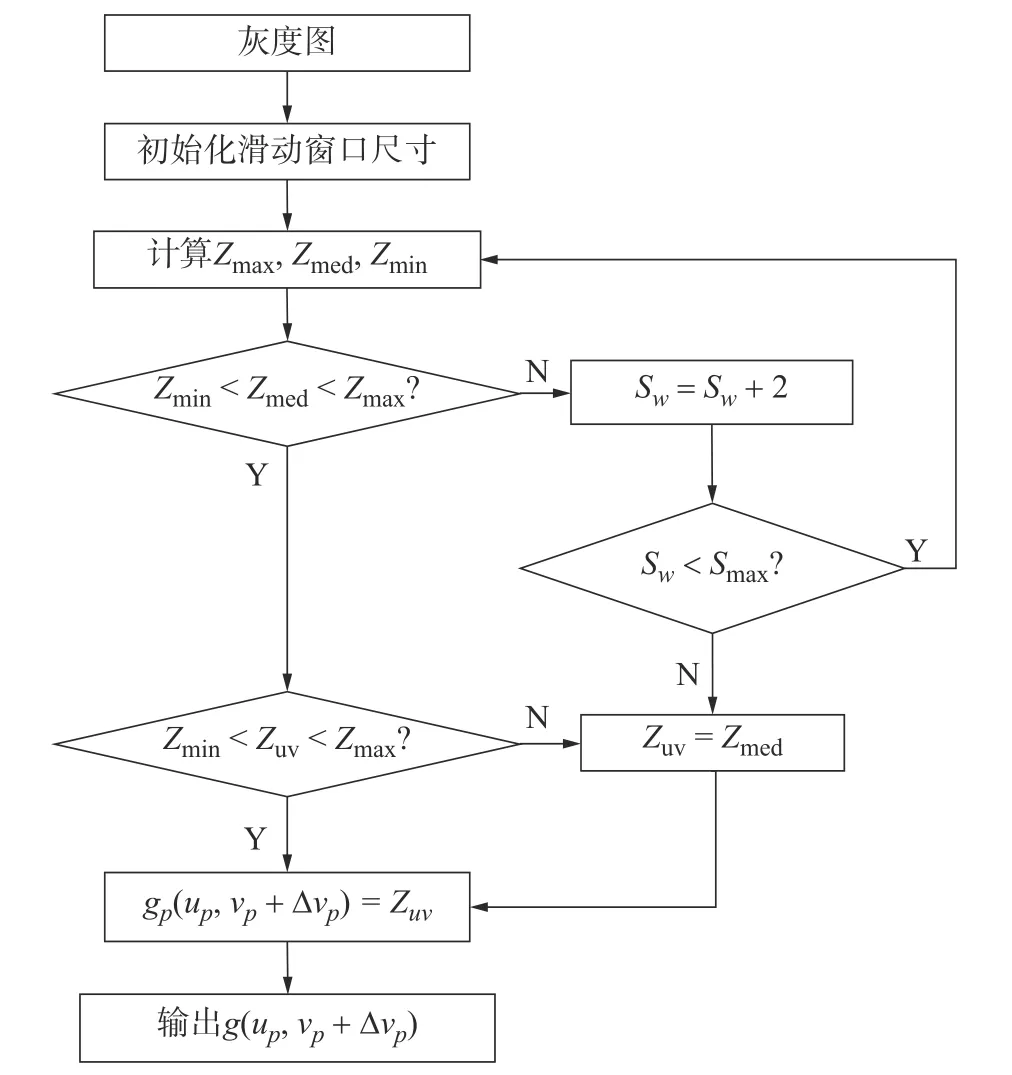
图8改进型自适应中值滤波流程
图8 中的符号定义如下:(upvp)T为图像中某一点像素的坐标;SW×SW为滑动窗口尺寸;Smax×Smax为 滑动窗口允许的最大尺寸; Smin×Smin为滑动窗口允许的最小尺寸; Zuv为(upvp)T位置的灰度值; Zmin、 Zmed、 Zmax分别为当前滑动窗口内所有像素灰度值的最小值、中值、最大值;g (up,vp+Δvp)为考虑机器人运动学后修正的滤波输出结果,即像素坐标( upvp+Δvp)处 的灰度值,其中Δ vP被定义为
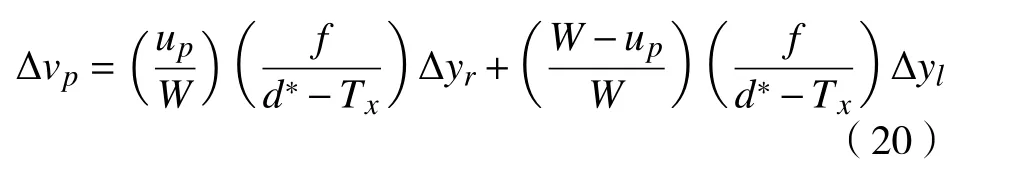
式中: W 为图像宽度; f为相机焦距; Δyr( Δyl)为输入角度为 φr( φl) 时,由式(7)计算得到的末端点 RG与点s1在 坐标系o -xy中沿y 轴方向的距离。
改进型自适应中值滤波利用式(20)引入双足单元运动学分析结果,在成像平面内修正图像。在利用图像计算单应性矩阵前,使用改进型自适应中值滤波器对图像进行预处理,降低足式移动机器人运动对成像过程的干扰,进而保证后续利用单应性矩阵估计机器人位姿的准确性。
3 控制方案设计
选择机器人位姿误差作为控制系统的输入状态变量,结合前文建立的系统模型和改进后的自适应滤波器,设计整个视觉伺服控制系统控制流程如图9所示。
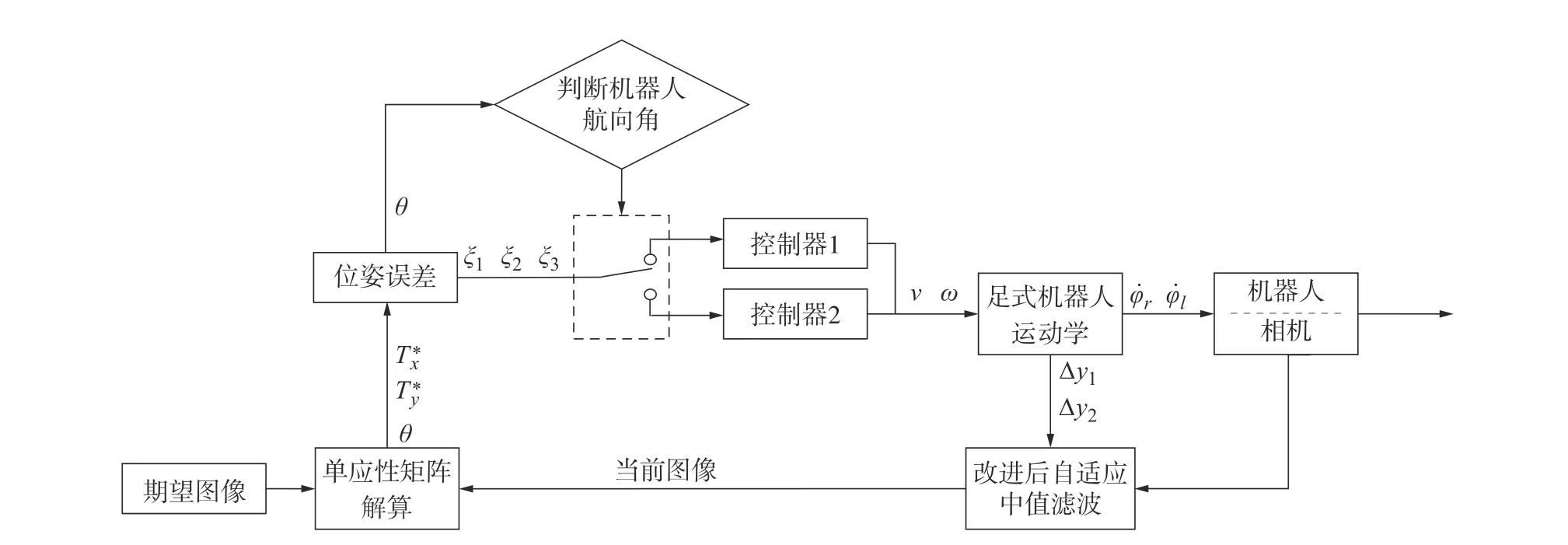
图9 控制系统框图
首先给定期望图像,结合当机器人在初始位姿处由单目相机获得的图像判断当前机器人航向角朝向;根据航向角朝向情况选择对应的控制器(1或2),输出机器人线速度 v和角速度 ω;再利用式(9)计算出两侧四足行走机构的输入角速度和,根据机构齿轮组传动比可进一步得到两侧电机的转速,驱动机器人移动;利用改进型中值滤波器对捕获的图像进行预处理,结合期望图像计算单应性矩阵,进而得到位姿误差,构成控制系统闭环,实现对足式机器人的反馈控制。
机器人航向角的朝向可分为图10所示的4种情况。对于第1种和第4种情况,即‖θ‖<‖ψ‖,使用控制器1控制机器人原地转动,直至不等式‖θ‖>‖ψ‖成 立;对于第2种和第3种情况,即‖θ‖≥‖ψ‖,使用控制器2驱动机器人由当前位姿向期望位姿移动,完成控制目标。

图10 机器人航向角朝向情况
控制器2为基于机器人位姿误差的机器人速度滑模控制器,以提高机器人由当前位姿趋近期望位姿过程中控制系统的鲁棒性。定义控制器滑模面为:

式中: sv和 sω分别为线速度控制器和角速度控制器所对应的滑模面; c1为正实数。
令滑模趋近率为:

式中: ε0、 k0和k1均为正实数。
由式(15)、式(21)和式(22)可得速度控制器:

根据式(23),选定合适的控制器参数 ε0、 c1、k1和k2后,控制器可利用位姿误差生成机器人线速度和角速度,再结足式机器人运动学分析结果,可进一步得到两侧电机的输出速度,实现对机器人运动的准确控制。为保证控制器能够使机器人最终移动到期望位姿,即3个位姿误差变量 ξ1、ξ2、ξ3全部趋向0,故构造李雅普诺夫函数对控制系统稳定性进行证明,其表述式为
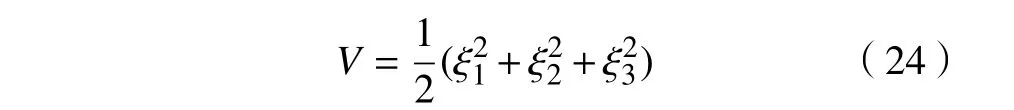
对式(24)两端求导,并将式(15)和式(23)代入求导后的公式中,经整理可得:
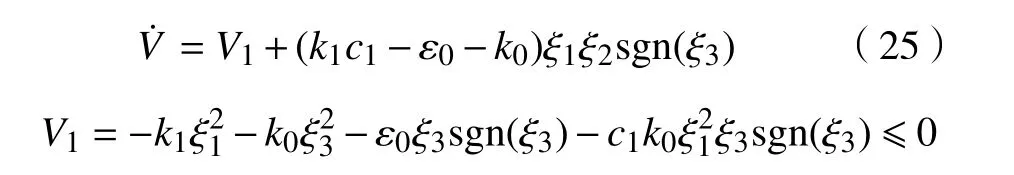
根据图7示出的 K 系与 K*系之间的关系可知Tx*≤0 ,Ty*sinθ ≥0,再由式(14)计算可得ξ1≤0;考虑到,使用滑模控制器控制机器人时, θ 满足‖θ‖≥‖ψ‖,因而有不等式 ξ1ξ2sgn(ξ3)≥0成立。故通过限制ε0、 c1、k1和k2的参数取值,保证不等式c1k1<ε0+k0成立,可使不等式V˙ ≤0成立且等号不恒成立,即可保证控制系统的全局稳定性。
4 实验与仿真验证
为验证上述方法的可行性与有效性,本节开展了基于四自由度移动平台的滤波器测试实验和基于CoppeliaSim 软件的控制系统虚拟仿真,分别验证所提出的改进型自适应中值滤波器和视觉伺服控制方法的有效性。
4.1 改进型自适应滤波算法验证
利用四自由度移动平台搭载单目相机,测试改进型自适应滤波算法,实验设备如图11所示。使用上位机可以设计移动平台各个轴的运动轨迹,并利用控制器驱动各个轴的伺服电机,实现平台运动,相机能够获取平台运动过程目标对象的实时图像。

图11 四自由度移动平台
利用式(7)可对式(20)中的 Δyr和Δyl进行求解,当机器人两侧四足行走机构的输入角度相位差变化时, Δyr和Δyl会令机器人机架平面产生的3类运动如图12所示,即垂直于地面的平移运动、绕机器人连体系 Kr中 Xr轴的翻滚运动和侧翻运动。与这3类运动对应的 Δyr与Δyl的运动轨迹如图13所示。
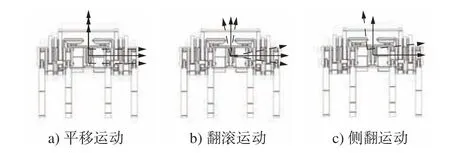
图12 机架平面运动
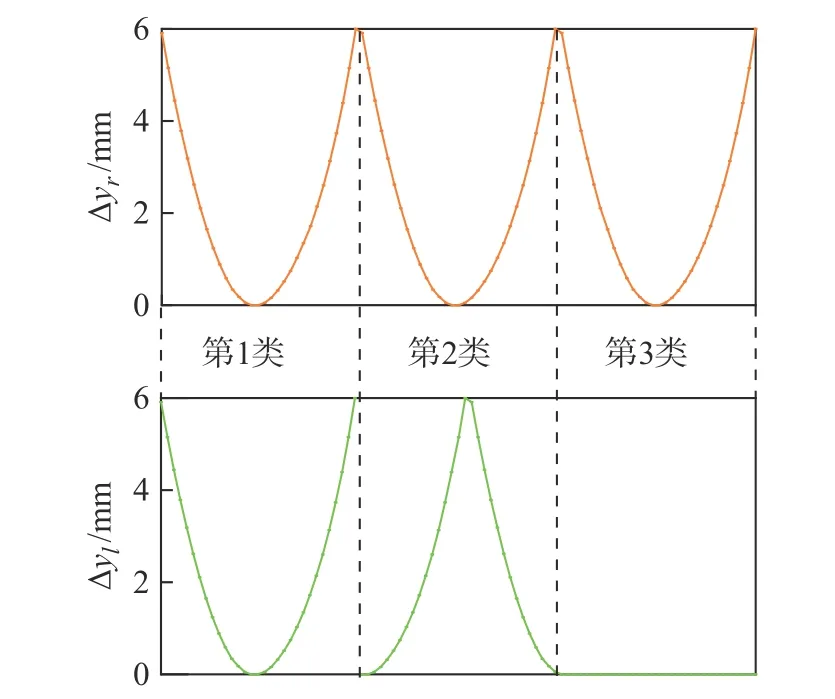
图13 Δyr 和Δyl 的运动轨迹
利用四自由度移动平台模拟机架平面的3类运动,以带有6个红色圆形图案的图片为目标,保存平台运动过程中的相机捕获的图像。当移动平台处于Δyr=0和 Δyl=0对应的位置时,将此时相机拍摄的图像选为参考图像。使用本文提出的改进型自适应中值滤波器对保存的图像进行处理,结合参考图像,利用1.3节中单应性矩阵分解方法计算相机位姿。实验结果如图14所示。
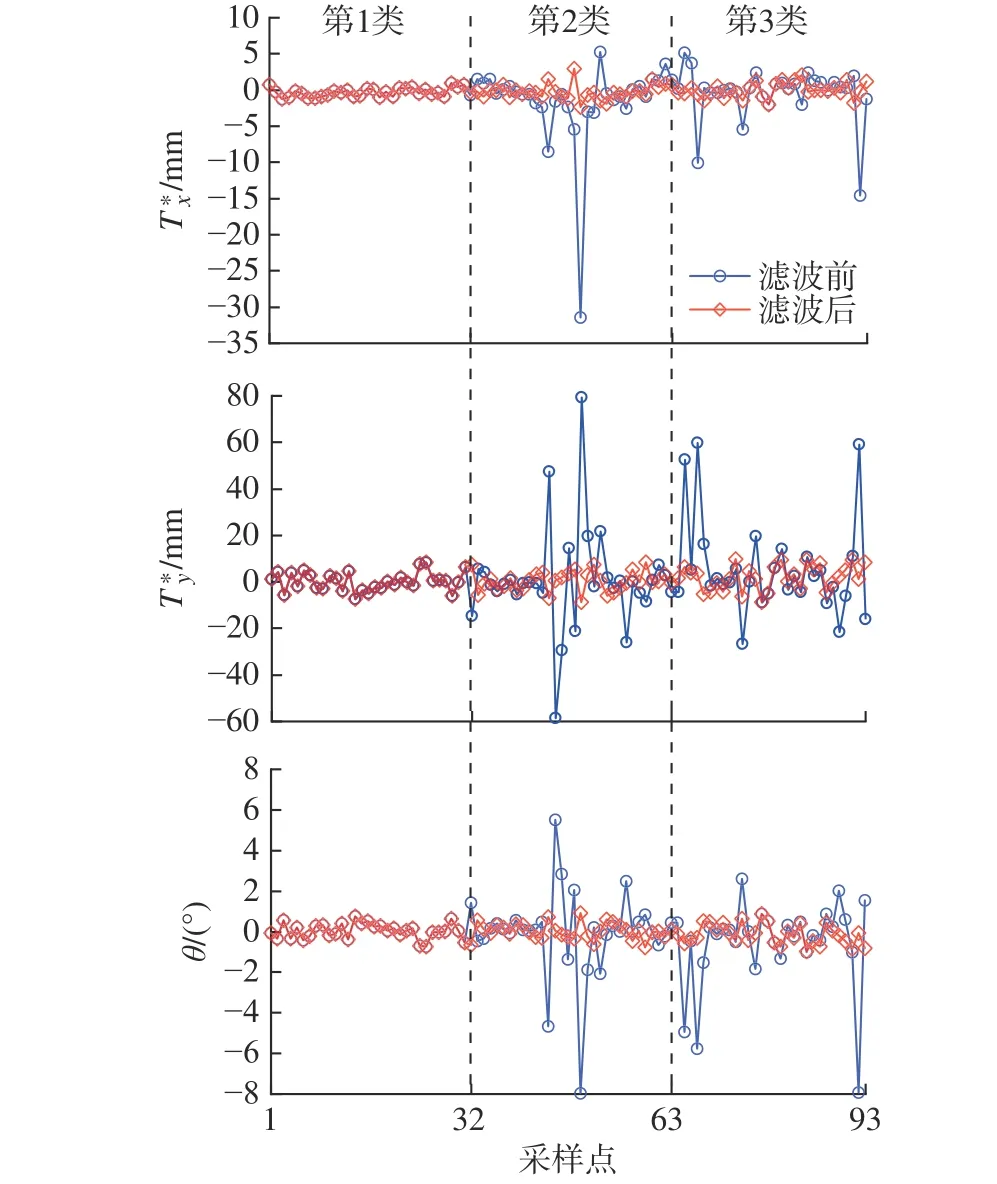
图14 滤波算法测试结果
由图14可知,机架平面翻滚和侧翻运动显著影响了位姿解算的精度,利用改进型中值滤波器能够有效降低这两类运动的干扰,提高位姿解算精度。滤波后,Tx*、Ty*和θ 与期望值的误差为±5 mm、±10 mm和±1°。
综上所述,改进型自适应中值滤波器通过引入四足行走机构运动学分析结果,可以有效减小周期运动对机器人位姿解算过程的影响,提高位姿解算精度。
4.2 控制方法仿真验证
为验证本文提出控制方案的有效性,本节采用仿真测试控制系统性能,利用机器人仿真软件CoppeliaSim 构建足式机器人虚拟模型,并搭建仿真场景模拟机器人运动情况。CoppeliaSim 是一款动力学仿真软件,利用软件提供的内嵌工具和物理引擎,可以快速灵活地搭建机器人仿真场景;借助RemoteAPI,可以采用C++语言实现控制器,实时控制软件中的虚拟模型。
仿真环境中相关设置如图15所示, Kg为仿真场景中的全局坐标系;足式机器人虚拟模型初始位置设置为(0 0.3 m 0.15 m)T,初始航向角偏差设置为25°;选择一张带有6个红色圆形的图片作为目标对象,并将图片放置于(1.4 m 0 0.15 m)T处;在(1 m 0 0.15 m)T处添加一个视觉传感器,提供目标对象的参考图像,同时将该位置设定为机器人的期望位置。
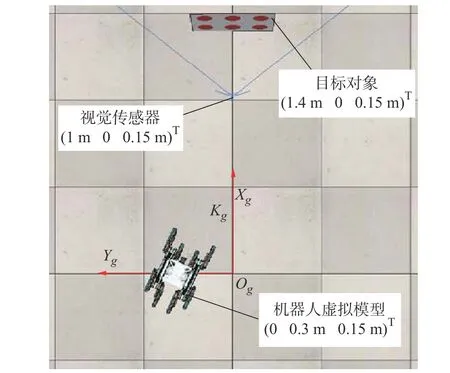
图15 机器人仿真场景
根据表1和表2中的机器人尺度参数以及表3中相机参数和控制器参数,完成对控制系统的初始化配置。利用本文提出的控制方案控制机器人移动,测量并采集机器人移动过程中相对Kg系的位姿。

表2 机器人尺度参数

表3 视觉传感器及控制器参数
机器人在仿真场景中的移动过程和视觉传感器捕获的图像如图16所示,仿真过程中机器人位姿轨迹采样结果如图17所示。由图17可知,相较于未考虑足式机构运动的控制系统,本文提出的控制方案能够更准确地使机器人沿理论轨迹移动到期望位置, Xg、 Yg和θ的实际轨迹与理论轨迹的均方根误差分别为0.028 m、0.012 m 和1.437°,与期望值的误差最终分别为0.013 m、-0.004 m 和1.067°。

图16 仿真中机器人的移动过程

图17 机器人位姿轨迹
综上所述,通过引入足式机构运动学,能够有效提高足式移动机器人视觉伺服控制系统性能,保证位姿收敛精度。
5 结论
本文针对一种足式移动机器人,提出了基于单应性的视觉伺服控制方案。
1)完成了足式移动机器人运动学分析,通过建立机器人移动速度与电机输出转速间的映射关系,使控制系统可以更精确地调整机器人运动。
2)为减小机器人四足行走机构竖直方向运动对视觉反馈环节的影响,提出了一种改进型自适应中值滤波器,使用四自由度移动平台开展实验,证明了该滤波器可以保障机器人位姿的估计精度。
3)通过设计机器人速度滑模控制器完成了足式移动机器人的视觉伺服控制方案,并利用仿真实验证明了本文所提出的控制方法可以更准确地控制足式移动机器人平稳移动到期望位姿。
基于本文提出的视觉伺服控制方案,我们接下来会将视觉控制技术用于足式机器人编队控制,使机器人在全局坐标不可测的环境中,仅利用图像信息定位自身位置,形成灵活的编队结构,完成探索任务。
