由两个同型部件和一个修理设备组成的系统的主算子的谱∗
2022-02-13艾尼吾甫尔
艾尼·吾甫尔
(新疆大学 数学与系统科学学院,新疆 乌鲁木齐 830017)
0 引言
由两个同型部件和一个修理设备组成的系统是我们常见的系统之一,例如两台功率一样的发电机连接构成的发电系统,两台功率一样的水泵连接构成的抽水系统,两台功率一样的计算机连接的计算系统等.2006年,曹晋华与程侃[1]给出了描述由两个同型部件和一个修理设备组成的系统的数学模型,并指出该系统是几个典型系统如两个同型部件并联的系统、两个同型部件的冷储备系统、两个同型部件的温储备系统、两个同型部件的表决系统等的推广,然后用Laplace 变换和Tauber 定理讨论了该系统的稳态可用度.2020年,艾尼·吾甫尔[2]讨论了文献[1]中的由两个同型部件和一个修理设备组成的系统.首先以修理时间作为补充变量并用Markov 过程推导了描述该系统的数学模型,然后在一定的条件下证明了该系统蕴含两个同型部件并联的系统、两个同型部件的冷储备系统、两个同型部件的温储备系统、两个同型部件的表决系统.第三步通过选择状态空间,主算子及其定义域将该系统的数学模型转化成了Banach 空间中的抽象Cauchy 问题.第四步当修复率µ(x) 为有界函数,即supx∈[0,∞)µ(x)<+∞时,证明了该抽象Cauchy 问题的主算子生成一个正压缩C0−半群,且该半群对包含该系统初值的一个集合是等距算子,由此推出了该系统存在唯一的概率瞬态解.第五步,当两个部件都故障的概率λ1和修复率µ(x) 满足时,0 是该系统的主算子的几何重数为1 的特征值.当µ(x) 是Lipschitz 连续并且存在正常数时,证明了该系统的主算子生成的C0−半群是拟紧算子.从而当µ(x) 是Lipschitz 连续并且存在正常数与使得时,该系统的时间依赖解指数(一致) 收敛于其稳态解.此外,给出了该模型的主算子的共轭算子的表达式并证明了0 是该共轭算子的几何重数为1 的特征值.最后,讨论了该系统的动态可用度并得到了:当µ(x) 是Lipschitz连续并且存在正常数时,该系统的动态可用度收敛于其稳态可用度.从而推广了文献[1]的结果.至今还没有发现该系统的时间依赖解的结构方面的研究.如果我们研究清楚该系统的时间依赖解的结构,那么我们能得到该系统的时间依赖解的渐近展开,数值分析等,从而给工程技术人员提供理论工具.而该系统时间依赖解的结构由该系统的主算子的谱分布决定.因此,该系统主算子的谱分布研究不仅理论上而且实际中具有重要的意义.因为文献[2]研究清楚了该系统的主算子在右半复平面和虚轴上的谱分布:右半复平面和虚轴上除了0 点外其他所有点都属于该主算子的豫解集,0 是该主算子及其共轭算子的几何重数为1的特征值,所以需要研究该系统的主算子在左半复平面中的谱.本文研究该系统的主算子在左半复平面中的谱分布.2002年,李学志等[3]在Hilbert 空间中研究了有界闭区间上建立的胎次递进人口方程的主算子的谱及其代数重数.在一定的条件下他们发现了该模型的主算子的特征值满足一个解析函数的零点,再用解析函数的零点定理证明了在左半复平面中的任何带形区域中该主算子至多有有限多个特征值,然后讨论了共轭算子的特征值并发现共轭算子的特征值也满足同样的公式,从而得到了共轭算子的特征值至多有有限多个,其次讨论了特征值的代数重数并得到了除了有限多个特征值外其他特征值的代数重数为1,由此给出了该方程的时间依赖解的渐近展开.由两个同型部件和一个修理设备组成的系统是在无界区间上建立的、有有限多个一阶偏微分方程构成的方程组[2].此外,根据该系统的物理背景发现该系统只能在非自反的Banach 空间中讨论[2].因此,文献[3]中的方法不适合本文研究的系统.
本文运用无界区间上的Riemann-Lebesgue 引理证明:在一定的条件下该系统的主算子在左半复平面中的任何带形区域至多有有限多个特征值,且这些特征值的几何重数为1.该系统的主算子的共轭算子在左半复平面中的任何带形区域至多有有限多个特征值,且这些特征值的几何重数为1.此外,结合本文的结果与文献[2]中的结果得到:0 是该系统的主算子及其共轭算子的严格占优特征值.
根据文献[1]和文献[2],由两个同型部件和一个修理设备构成的系统由以下方程组描述:
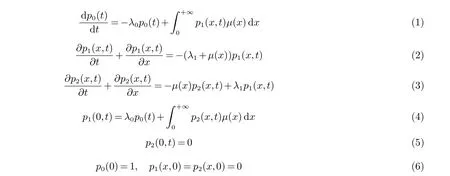
其中:(x,t)∈[0,+∞)×[0,+∞);λ0表示一个部件故障的概率;λ1表示两个部件都故障的概率;µ(x) 表示修复率,满足µ(x)≥0,表示两个部件都完好的概率;p1(x,t) 表示在时刻t 系统中一个部件故障并且正在修理的部件已消耗的修理时间为x 的概率;p2(x,t) 表示在时刻t 系统中两个部件都故障并且正在修理的部件已消耗的修理时间为x 的概率.
本文沿用文献[2]中的记号.记

选取状态空间为

用Banach 空间的定义不难验证X 是一个Banach 空间.以下定义算子及其定义域.

若对p ∈D(A) 定义

且对p ∈X 定义
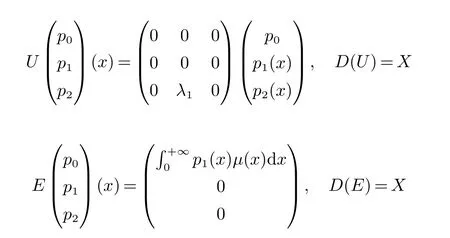
则方程组(1)~(6) 可以改写为Banach 空间X 中的一个抽象Cauchy 问题[2]:
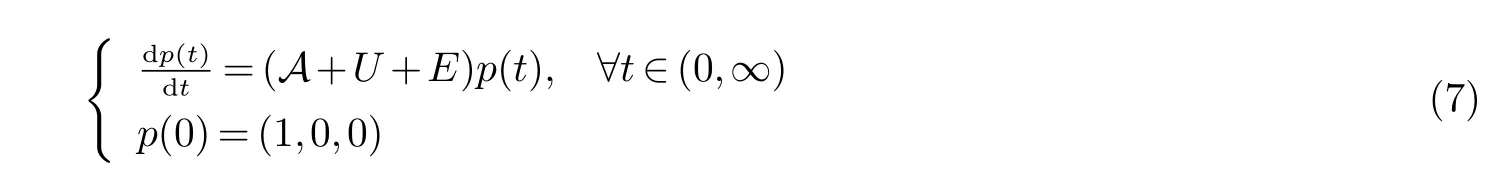
1 主要结果
引理1 使函数解析的任何带形区域中A+U+E至多有有限多个特征值,并且这些特征值的几何重数为1,其中表示γ 的实部.
证明考虑特征方程(A+U+E)p=γp,即

解(9) 与(10) 得到

合并(12) 与(14) 并用(13) 推出
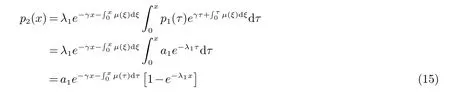
将(13) 代入(8) 有
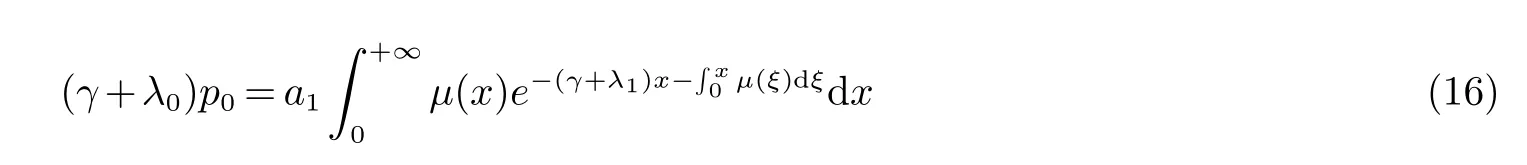
结合(13) 与(11),(15) 并用(16) 可得
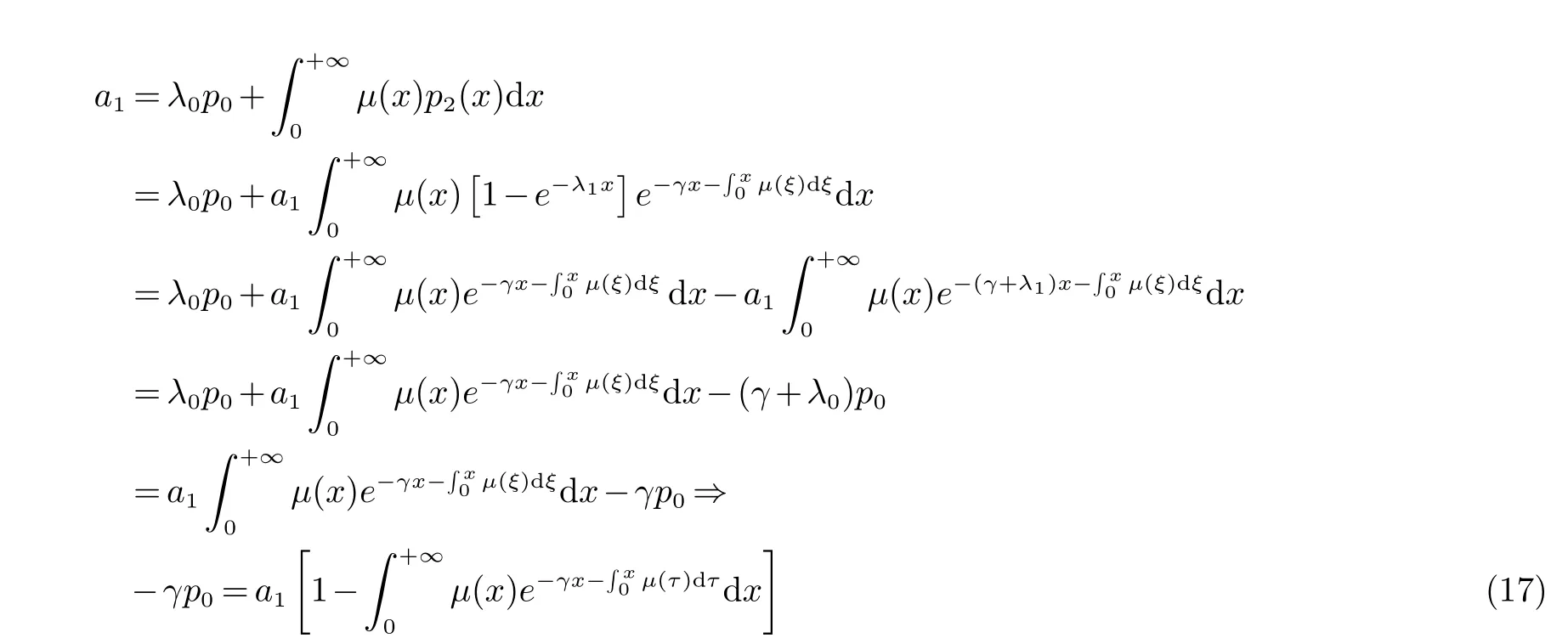
若p0=0,则由(16) 知道a1=0,从而由(15) 与(13) 容易看出p(x)=(p0,p1(x),p2(x))=(0,0,0),即γ 不是特征值.
(16) 与(17) 蕴含

(16)×γ+(17)×(γ+λ0) 给出

则由(19) 易知

由(13) 与(15) 估计出
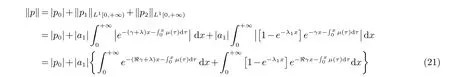
由此式与(18),(20)知道:满足F(γ)=0 的γ 都是A+U+E 的特征值.因为F(0)=0,所以γ=0 是A+U+E的特征值.这是文献[2]中的结果.我们发现文献[2]中的条件可以去掉,因为
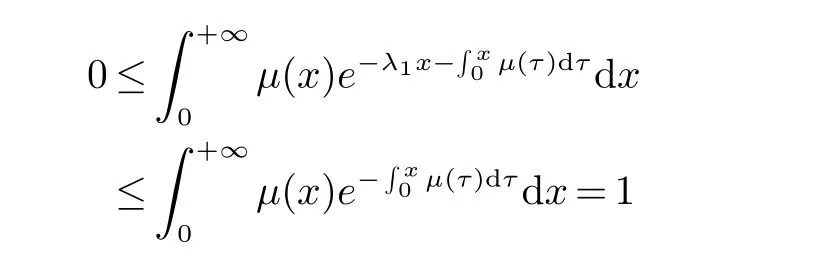
由引理1的条件知道F(γ) 在带形区域Ω={γ ∈C|γ=b+ic,b1≤b ≤b2≤0} 中解析,所以由解析函数的零点定理得到F(γ) 至多有可数个零点.
以下用反证法证明引理1的结果.假设A+U+E 在带形区域Ω={γ ∈C|γ=b+ic,b1≤b ≤b2≤0} 中有无穷多个特征值,那么F(γ) 在Ω 中有无穷多个根,设这些根γk=bk+ick,k ≥1,i2=−1.由Bolzano-Weierstrass 定理知道存在子列γn=bn+icn使得limn→∞bn=b0,limn→∞cn=∞,F(γn)=F(bn+icn)=0,即

(23) 的两边取n →∞的极限,由Riemann-Lebesgue 引理得到∞=0,矛盾.这说明cn是有限数,即γn=bn+icn是有限多个.由(13) 与(15) 容易看出这些特征值的几何重数等于1.
文献[2]中给出了X 的共轭空间
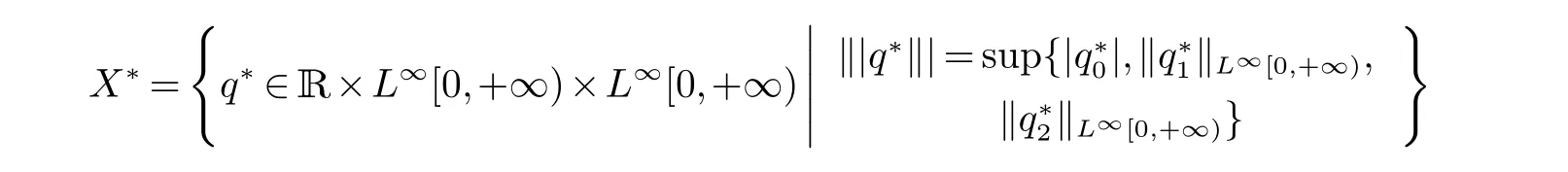
它是一个Banach 空间.A+U+E 的共轭算子(A+U+E)∗为

引理2使函数解析的任何带形区域中(A+U+E)∗至多有有限多个特征值并且这些特征值的几何重数为1.
证明考虑特征方程(A+U+E)∗q∗=γq∗.这等价于
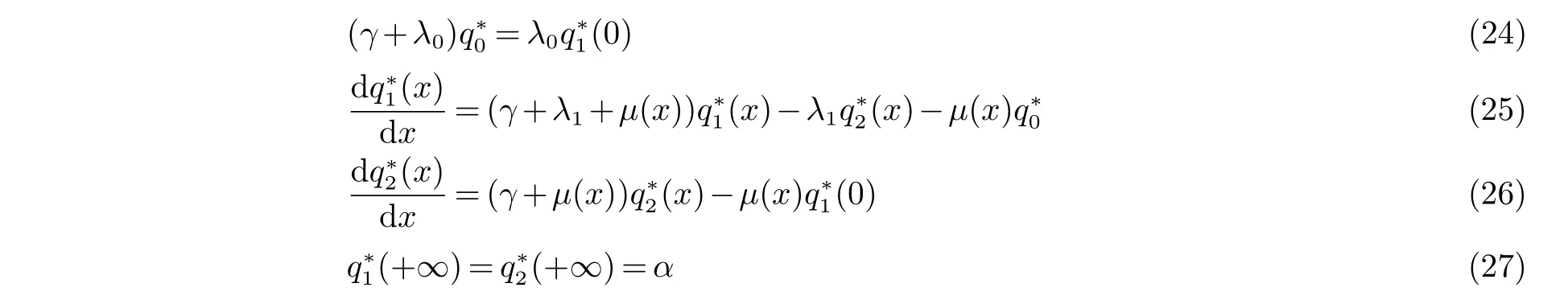
解(26) 得到

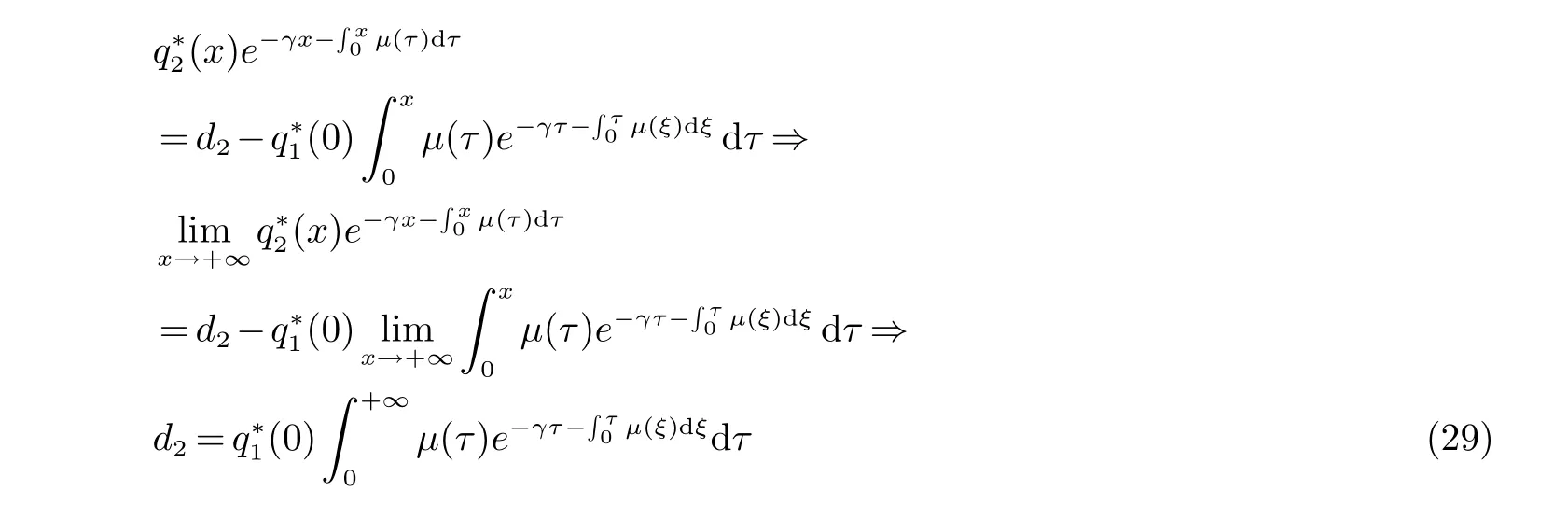
将此式代入(28) 并用积分的区间可加性求出
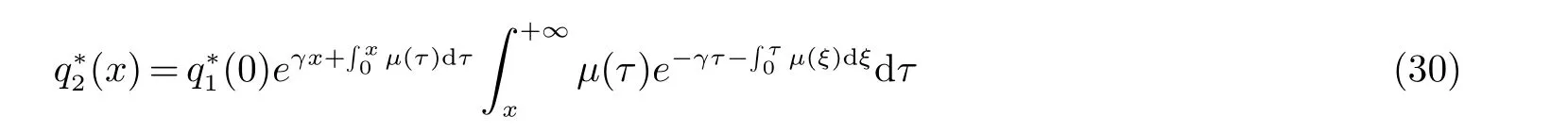
解(25) 我们有

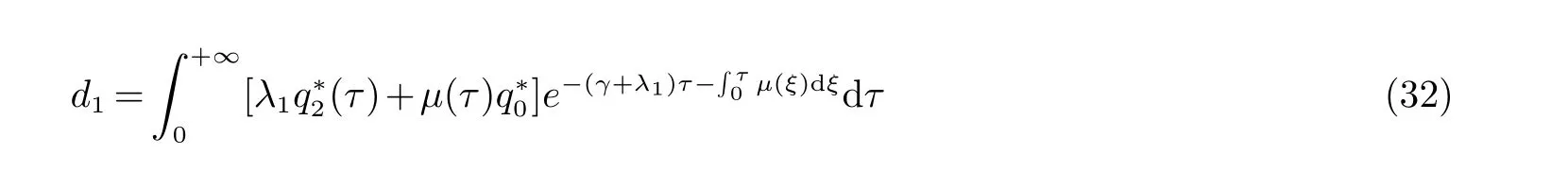
将(32) 代入(31) 并用(30) 和Fubini 定理计算出

此式蕴含

由(30) 与(33) 估计出
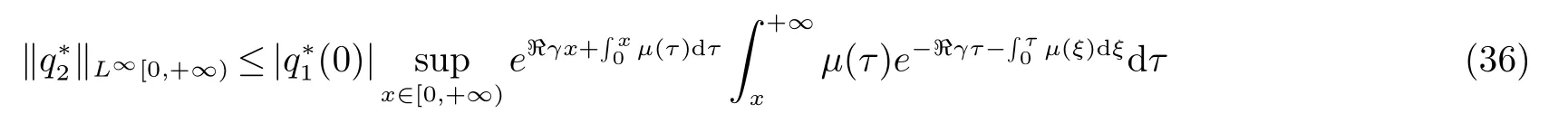

由(36),(37),(35) 与(24) 知道:满足F(γ)=0 的所有γ 都是(A+U+E)∗的特征值.用引理1 的方法得到F(γ) 在带形区域{γ ∈C| −∞ 综合以上两个引理与文献[2]得到本文的主要结果: 定理1(1)使函数解析的任何带形区域{γ ∈C|−∞ (3) 0 是A+U+E 的严格占优特征值. (4) 0 是(A+U+E)∗的严格占优特征值. 注解1如果存在正常数<+∞,那么F(γ) 在内解析.从而,由定理1 知道A+U+E 与(A+U+E)∗在带形区域中至多有有限多个特征值并且这些特征值的几何重数为1. 定理1 的思想和方法对有限多个偏微分方程描述的可靠性模型[4−6]适用,对无穷多个偏微分方程描述的可靠性模型[7−8]和排队模型[9]不适用.
