改进狼群算法求解多目标柔性作业车间调度问题∗
2022-02-13陈嘉朋张宏立
陈嘉朋,张宏立,王 聪,马 萍
(新疆大学 电气工程学院,新疆 乌鲁木齐 830017)
0 引言
柔性作业车间调度问题(Flexible Job-shop Scheduling Problem,FJSP)[1]是一类复杂的NP-hard优化问题,其难点在于需要同时考虑作业车间的加工次序和加工机器.随着对FJSP的研究不断深入,更符合实际需要的多目标柔性作业车间调度问题(Multi-objective Flexible Job-shop Scheduling Problem,MOFJSP)[2]成为目前的研究热点.在研究多目标柔性作业车间调度问题时,MOFJSP满足更多的约束条件,同时各个目标函数之间互相制约,导致各个目标函数值很难同时达到最优.所以,MOFJSP是更难的NP-hard优化问题.
许多学者针对MOFJSP进行了广泛和深入的研究.Huang[3]等人将粒子群算法和遗传算法巧妙融合,通过教与学的方式体现混合算法求解MOFJSP的有效性;朱光宇[4]等人将灰熵并行分析引入粒子群算法对多目标柔性作业车间调度问题进行求解,通过测试验证了灰熵并行法的有效性;朱伟[5]等人运用遗传算法(Genetic Algorithm,GA)来优化以加工总成本和最大加工时间为目标的MOFJSP,通过对算法算子、编码结构、自适应变异规则的改进和更新,算法和模型的鲁棒性和有效性得以提高;赵博选[6]等人提出一种多策略融合Pareto人工蜂群算法来求解MOFJSP,多种搜索策略互相融合,不仅使算法实现了人工蜂群的自主与协同搜索,而且达到了全局探索与局部寻优的平衡效果.上述智能优化算法为MOFJSP的求解开辟了新的研究方向和思路,但算法求解全局最优解的能力有待进一步提高.
为解决传统群智能优化算法在求解MOFJSP时存在易陷入局部最优、算法后期收敛速度慢等问题,本文使用吴虎胜等人提出的一种新型群智能优化算法——狼群算法[7],并将量子粒子群算法中的三个重要参数与其融合,得到一种新的混合优化算法对MOFJSP进行求解.狼群算法模拟狼群猎食行为及猎物分配方式,抽象出“游走”“召唤”“围攻”3种智能行为和“胜者为王”的头狼产生规则及“强者生存”的狼群更新机制.狼群算法结构清晰,寻优策略丰富,特别是针对多峰、高维的目标函数有着较好的求解性能,这些优势使算法在时间序列预测[8]、故障诊断[9]等方面有着广泛的应用,但狼群算法在寻优过程中,也存在算法后期收敛速度慢、易陷入局部最优的问题.
本文针对狼群算法寻优过程中存在的问题,提出一种将量子粒子群算法中能够引导粒子以较快的收敛速度,在一定的搜索范围内朝着全局最佳位置不断靠近的三种性能参数与狼群算法融合的混合优化算法来求解MOFJSP.创新点主要为:
(1)种群初始化.将高斯分布的概率密度函数运用于种群初始化,以得到质量较高的初始种群.
(2)搜索策略.将量子粒子群算法中的吸引子、收缩扩张系数、势阱特征长度三个重要参数和狼群算法融合,增强算法的全局搜索性能和收敛速度;采用物元分析法更新种群,提高种群的自适应能力.
(3)最优解操作.通过局部邻域搜索,给予最佳序列充分的计算资源,以增强算法的全局搜索性能.
1 MOFJSP问题描述和数学模型建立
1.1 问题描述
FJSP描述如下:m个工件在n台机器上加工,每个工件至少有一道加工工序,每道工序可以选择不同的机器进行加工,不同工序的加工时间取决于所选机器的性能.表1为FJSP的一个加工实例.

表1 FJSP加工实例
1.2 建立FJSP数学模型
1.2.1 数学变量定义
m为工件数;n为机器数;i为工件序号,i=1,2,3,···,m;j为机器序号,j=1,2,3,···,n;Ci为每个工件的完工时间;Cmax为最大完工时间;Oih为第i个工件的第h道工序;Mih为第i个工件的第h道工序的可选加工机器数;Mjih为第i个工件的第h道工序在机器j上加工;Pjih为第i个工件的第h道工序在机器j上的加工时间;Tih为第i个工件的第h道工序开始加工时间;Cih为第i个工件的第h道工序加工完成时间;Sjih为Mjih对应的加工时间;L为工序序号,L=1,2,3···,hi;xjih=1,工序Oih选择机器j进行加工;xjih=0,工序Oih不选择机器j进行加工;yihjkl=1,工序Oih先于工序Ojkl进行加工;yihjkl=0,工序Oih晚于工序Ojkl进行加工.
1.2.2 MOFJSP调度指标
(1)最大完工时间
最大完工时间是指所有工件均被加工之后,最后离开机器的一道工序所对应的完工时间.性能指标通常表述为:

其中:Ci代表每个工件的完工时间.
(2)机器总负荷
机器总负荷是指所有工件均被加工完成之后,工件在机器上的加工时间总和.

(3)瓶颈机器负荷
瓶颈机器负荷是指所有工序被加工完成之后,负荷(加工时间)最多的机器所用的时间.

2 算法介绍
狼群算法(Wolf Pack Algorithm,WPA)是基于狼群智能行为的新型优化算法,算法基本思想是“任务分配,各尽其职”和“弱肉强食,适者生存”.算法意在通过模拟自然界的生物种群行为由概率模型搜索最优解.量子粒子群算法(Quantum Particle Swarm Optimization,QPSO)是一种考虑量子行为的粒子群算法,该算法相较于传统的粒子群算法,具有更好的收敛速度和全局搜索性能.将QPSO中的三种重要性能参数与WPA相结合,以形成改进狼群算法对多目标柔性作业车间调度问题进行求解.狼群位置更新分为三个阶段,分别为探狼游走、头狼召唤和猛狼围攻.三个阶段的主要改进位置更新公式如(4)、(5)和(6)所示:

式(4)为探狼游走位置更新公式.探狼在搜索空间中朝着猎物气味浓度更深的方向不断游走,以获取最佳位置.当探狼达到最大游走次数时,选择最佳目标函数值的狼为新头狼.为使探狼进行更为精细的搜索,扩大种群的搜索范围,避免算法陷入局部最优,将收缩扩张系数β和归一化因子w引入探狼游走行为.

式(5)为猛狼奔袭更新公式.QPSO中粒子i的吸引子s(i)能够使粒子以较快的速度朝着最佳粒子不断移动,以提高算法的收敛速度和全局搜索性能.

狼群在围攻猎物的过程中,容易超出设定的搜索空间范围,得到不可行解,从而导致算法的求解性能下降.将势阱特征长度Li引入狼群围攻行为的位置更新公式,如式(6).势阱特征长度Li能够使参与围攻行为的个体处在有效的搜索空间内.
2.1 种群更新机制
采用物元分析法,对猎食之后的种群进行更新和保存操作,以满足更优的解进入种群下一次迭代.在物元分析中,物元R=(M,C,X),M代表物元的名称,C代表特征,X代表特征对应的物元量值.将个体对应的位置放入物元特征,将位置更新操作放入物元名称,所得到的新适应度函数值作为物元量值.矩阵Rmn为n个m维物元矩阵.

其中:C1,C2,C3···Cm为捕猎之后个体对应的位置;M1,M2,M3···Mn为不同位置下的不同更新策略;fit()为不同位置更新之后的适应度函数值.
以C1为例:
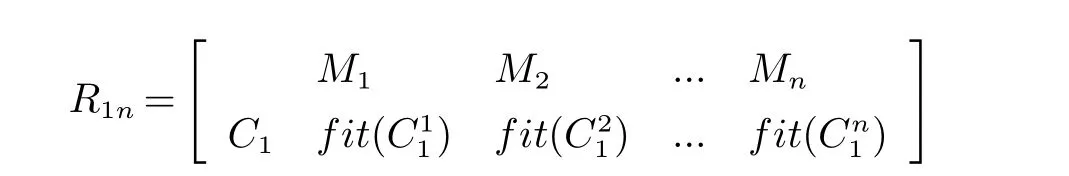
3 编码和解码
3.1 种群初始化
初始种群的质量对种群迭代过程中的收敛速度以及全局最优解的求解起到重要的作用,生成一个较高质量的初始种群十分关键.本文采用高斯分布的概率密度函数[10]产生随机变量来调整加工序列,从而对种群进行初始化.采用的概率密度函数为:

其中:µ为均值,表示概率密度函数分布曲线的对称轴;σ为标准差,表示对称轴到左右两边曲线的某一宽度.
初始化操作
Step1设置x1=rand(0,1),σi=rand(0,1),µi=rand(-1,1),i=1,2,3···L,L为总工序数.保持x1不变,将L组(σi,µi)带入f(x),得到一组随机序列[f1(x1),f2(x1)···fL(x1)],对应初始加工工序;
Step2将[f1(x1),f2(x1)···fL(x1)]进行升序排列,同时将初始加工工序随着变量的升序进行调整,得到新的加工工序.
通过重复Step1到Step2,直到产生与种群规模相同的初始加工工序.利用高斯分布的概率密度函数产生随机数序列的方式来进行种群初始化,可以使初始种群个体离散地分布在解空间内,有效提高了初始种群的质量和多样性.种群初始化过程如表2所示.

表2 种群初始化
3.2 编码和解码
为更好满足工艺路线的约束,本文采用双层编码方式进行编码.基于表1,工序编码为(113322),表示O11、O12、O31、O32···,以此类推;设机器编码为(113212),表示O11选择机器1,O12选择机器1,O13选择机器3,O21选择机器2···以此类推(Oij代表工件i的第j道工序).
工序解码
根据Logistic映射方程[11],产生一组随机均匀的随机数S1.S1对应相应的加工工序.将S1升序,并得到对应索引值.升序时,若S1出现相同的数值,以左(小数值)进行优先排序.S1进行升序后,计算S(new)=S1×(G÷V),G为工件总数,V 为工序总数.当S(new)为小数时,将其朝着比自身大的方向进行取整.S(new)对应相应的工件号.表3为工序解码过程.

表3 工序解码
机器解码
设工件i的第h道工序为u;第i个工件的第h道工序开始加工时间为ST(u),加工时间为Tp,则完工时间为ST(u)+Tp;该工序的工件前任工序和机器前任工序分别用JP(u)和MP(u)表示.则有:

本文采用贪婪策略对机器进行解码.选择使ST(u)+Tp最小的机器加工,若出现机器的加工时间相同,则选择使Tp最小的机器加工.
3.3 最佳序列更新机制
本文采用邻域结构搜索策略,给予最佳序列充分的计算资源,不断提高算法寻求全局最优解的能力和收敛速度.
NS1:随机选择工序码的两个位置进行交换;
NS2:随机选择工序码的一个位置为交换点,将两端的序列直接旋转交换;
NS3:随机选择工序码的一个位置,将其对应的数值从工序码中剔除,再随机插入剩余序列的任意位置;
NS4:将原工序码整体进行倒序操作;
NS5:任意选择工序码的一个位置数值i变为i+1(i/=i(max)),同时任意选择工序码的一个位置数值i+1变为i.
4 多目标策略
本文通过计算种群个体的非支配等级[12]和拥挤度的方法,对狼群中的最优解和最劣解进行保存,便于狼群在迭代过程中个体狼的位置更新.
4.1 计算个体非支配等级
对于种群规模为N(t)的种群P,t为迭代次数.具体操作步骤如下:
Step1设i=1;
Step2对于所有的j=1,2,3···N(t),且j/=i,基于个体的适应度函数比较个体i和个体j之间的非支配和支配关系.如果所有个体j均不优于个体i,则将i判定为非支配个体;
Step3令i=i+1,返回Step1,直到找出所有的非支配个体.
通过Step1至Step3得到第一层的非支配解集.然后,剔除第一层非支配解集对剩余个体重复Step1至Step3,得到第二层非支配解集···直到种群被分层.种群规模随着迭代次数,不断进行更新操作.
4.2 计算个体拥挤度
拥挤度即为拥挤距离,是指单个Rank层中个体的密集程度.计算个体拥挤度是为了得到同一等级Pareto解的优先级关系,拥挤度计算公式如下:

其中:V 为目标函数的个数,fv(i−1)和fv(i+1)为该个体排序之后前后两位目标函数值;fmaxv为某一目标函数的最大值;fminv为某一目标函数的最小值.当个体i的拥挤度ndi大于个体j的拥挤度ndj,则个体i占优.
5 IWPA解决MOFJSP步骤
Step1种群初始化.设置种群规模、迭代次数、探狼比例因子、探狼初始游走方向数、步长因子等参数.计算个体非支配等级以及个体拥挤度后对个体进行排序,选出适应度值最佳的狼为头狼,并对头狼采用最佳序列机制进行调整(在种群更新和迭代的过程中,只要产生头狼,就使用最佳序列更新机制,更新头狼),其余个体狼分别为探狼和猛狼;
Step2种群迭代.探狼位置更新;头狼召唤猛狼,猛狼位置更新;然后计算猛狼和当前新头狼之间的距离,判断猛狼是否转入猎物围攻行为;围攻猎物之后,使用物元分析法更新种群,再次计算个体的非支配等级和拥挤距离,选出最佳个体为种群新头狼;
Step3判断是否满足要求,若满足算法输出条件,则输出对应的最优解以及适应度函数值;若不满足,返回Step2.
6 仿真测试及分析
仿真实验采用MATLAB 2018b实现,运行环境:处理器Core i5-8265U@1.60 GHz,Windows10操作系统.IWPA参数设置如下:设置探狼比例因子为3,探狼每一次游走的方向数最小值为4,最大值为10;步长因子为200;改进狼群算法的种群规模和最大迭代次数等基本参数和比较算法保持一致.
为了验证IWPA的优势,本文选择3种不同规模的算例,使用不同文献中的算法进行求解比较.3种算例分别为:Kacem1、Kacem2、Kacem3.参考文献分别为:混合人工蜂群算法(Hybrid Artificial Bee Colony Algorithm,HTABC)[13]、状态转移算法(State Transition Algorithm,STA)[14]、改进入侵杂草优化算法(Improve Invasive Weed Optimization Algorithm,IIWO)[15]、多种邻域结构杂草优化算法(Multiple Neighborhood Structures Weed Optimization Algorithm,MNSEO)[16]、狼群算法(Wolf Colony Algorithm,WPA)、灰狼算法(Grey Wolf Optimization,GWO).对比结果如表4所示.
从“非劣解组数”“单目标最优解”“Pareto占优”三个层面对表4进行分析.

表4 多种算法结果比较
(1)非劣解组数
算法求出的非劣解组数较多,可以体现出算法有较好的求解性能.针对Kacem1算例:IWPA可以求出3组非劣解,和HTABC求解性能相同,强于IIWO、STA、MNSEO、GWO、WPA;针对Kacem2算例:IWPA可以求出5组非劣解,和MNSEO求解性能相同,强于HTABC、IIWO、STA、GWO、WPA;针对Kacem3算例:IWPA可以求出3组非劣解,和HTABC求解性能相同,强于IIWO、STA、MNSEO、GWO、WPA.
(2)单目标最优解
通过比较单目标最优解,可以从整体性能上判断算法的优劣.将每种算法求出的Pareto解集中的单个目标的最优解进行取出合并,构成单目标最优解.针对Kacem1算例,IWPA求出非劣解的能力要强于HTABC、IIWO、STA、WPA、GWO;针对Kacem2算例,IWPA求出非劣解的能力要强于HTABC、IIWO、STA、MNSEO、GWO、WPA;针对Kacem3算例,IWPA求出非劣解的能力要强于HTABC、STA、WPA,和GWO能力大致相同.
(3)Pareto占优
比较不同算法之间的Pareto占优关系,对算法求解Pareto解集的能力进行综合判断.通过Pareto占优分析可知:针对Kacem1算例,IWPA求出非劣解的能力要强于WPA、GWO、IIWO,和STA大致相同,弱于HTABC;针对Kacem2算例,IWPA求出非劣解的能力要强于其他5种对比算法,和MNSEO大致相同;针对Kacem3算例,IWPA求出非劣解的能力要强于WPA、GWO、STA,弱于HTABC.针对Kacem3算例,选择一组非劣解集,使用IWPA画出相应的甘特图,如图1所示.
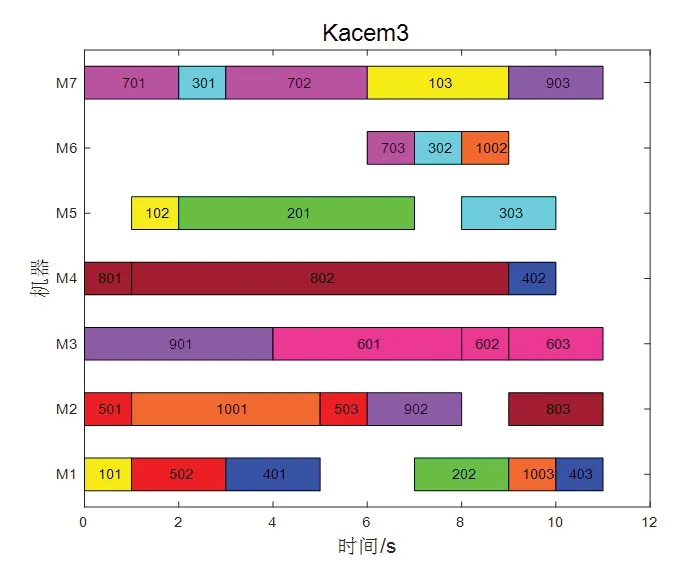
图1 Kacem3调度甘特图
通过“非劣解个数”“单目标最优解”“Pareto占优”三个层面进行分析,可以得到:
(a)IWPA能够求出较多组数目的Pareto解集,求取的非支配解的数目越多,被选择为Pareto最优解的可能性就越大;
(b)IWPA有较好的单目标最优解,通过与其他智能优化算法所得结果进行比较,可以看出本文的IWPA具有一定的求解优势.针对Kacem1算例,IWPA求出的单目标最优解为(11,31,8),较其他算法有较强的求解优势;针对Kacem2算例,IWPA求出的单目标最优解为(14,73,11),IWPA求出非劣解的能力要强于HTABC、IIWO、STA、MNSEO、GWO、WPA;针对Kacem3算例,IWPA求出非劣解的能力要强于HTABC、IIWO、STA、MNSEO、GWO、WPA;IWPA在Pareto占优层面,也具有较强的寻优优势,能够向组合后的单目标最优解提供较多的选择.
7 结论
本文基于狼群算法的基本结构和寻优优势,提出一种将量子粒子群算法的重要参数和狼群算法融合的混合优化算法对多目标柔性作业车间调度问题进行求解.
(1)新型混合优化算法使寻优种群在一定的搜索范围之内,以较快的收敛速度朝着全局最优个体不断靠拢,算法求解全局最优解的能力得以增强;
(2)采用高斯分布的概率密度函数对种群进行初始化,提高初始种群的质量和多样性;通过最佳序列调整机制,不断更新最优解的同时也提高了算法的收敛速度;
(3)物元分析法丰富了种群的更新策略,有利于种群的迭代进化.
通过以上分析,可知本文所提出的混合优化算法对求解MOFJSP具有一定的合理性和优势.笔者将在本文研究基础之上,进一步探究混合狼群算法应用于不确定因素影响、动态重调度等更加复杂的车间调度问题.
