基于加权平均樽海鞘群算法和BP神经网络的COVID-19预测∗

胡红萍，乔世昌，孔慧华，徐乔王，白艳萍

(1.中北大学 理学院，山西 太原 030051；2.临汾市财政局 国际金融组织贷款服务中心，山西 临汾 041000)

0 引言

新型冠状病毒肺炎（Corona Virus Disease 2019,COVID-19）由于其高传染性和高致病性，严重威胁到了人类的生命安全，并已迅速蔓延到全球，成为全球关注的问题之一.自疫情暴发以来，我国进行了全民总动员，真正做到“早发现，早隔离”.但由于境外输入COVID-19和无症状感染的影响，疫情防控仍然面临反弹压力.因此有效地预测COVID-19的累计确诊人数对COVID-19的防控具有非常大的价值.

目前，常用的预测方法有差分自回归移动平均乘积季节模型[1]，群智能算法优化神经网络模型[2−3]，多尺度组合模型[4]，随机森林算法和模糊信息粒化的混合算法[5]，经验模态分解和极限学习机的组合预测模型[6]，等等.随着群智能算法和机器学习的不断改进，预测模型也随之增加，更利于解决实际问题.如用萤火虫算法优化长短时记忆神经网络，并利用其预测生猪价格[2]；将粒子群算法和差分进化相结合优化自适应小波神经网络的初始化网络参数，进而对风电功率超短期多步预测[3]；利用改进的灰狼算法优化Elman神经网络，对基于基因表达谱的乳腺癌进行识别[7]；利用改进粒子群算法优化BP神经网络对甜菜产量进行预测[8]等.

最近很多学者将群智能算法和机器学习相结合对COVID-19进行预测.例如，文献[9]利用机器学习、自适应神经模糊推理系统和增强甲虫天线搜索群智能元启发式相结合的混合方法预测COVID-19确诊人数；文献[10]利用递归神经网络对COVID-19确诊人数进行预测；文献[11]利用集合经验模态分解和自回归移动平均模型对COVID-19全球预测系统预测结果进行改进.

樽海鞘群算法（Salp Swarm Algorithm,SSA）是受深海中樽海鞘的航行和觅食行为启发提出的[12].自SSA提出以来，研究者已对SSA做了很多改进.例如，将SSA中樽海鞘链的领头者的搜索方式修改为贪婪的交叉选择方法，加强了SSA的性能且避免陷入局部最优[13]；将正余弦算法和干扰算子加到SSA得到了一种特征选择方法[14]；将混沌映射加入SSA中代替随机数建立了混沌SSA（CSSA），并且将CSSA与2维曲波变换和深度学习技术相结合用于X射线图像对COVID-19进行诊断[15]；将SSA的樽海鞘的位置更新修改为Singer的混沌映射，在开发阶段使用局部搜索算法，得到动态的SSA[16].

本文针对其他樽海鞘对链中第i个跟随者均有影响的问题，提出加权平均樽海鞘群算法（Average Salp Swarm Algorithm,AVSSA），并通过23个基准函数验证AVSSA的有效性，进而用AVSSA优化BP神经网络的权值和偏差，建立预测境外输入COVID-19的预测模型AVSSA-BP.

1 樽海鞘群算法

樽海鞘群算法是受深海中樽海鞘的航行和觅食行为的启发提出的[12].樽海鞘有透明的桶形身体，其组织非常类似于在海洋中发现的水母，它们像水母一样通过身体泵水前进.SSA是从樽海鞘的群体行为中获得的，它是以樽海鞘群体构成一个樽海鞘链，在该链中，第一个樽海鞘为领导者，其余的樽海鞘为跟随者.

设F是n维搜索空间中的食物源，将其作为樽海鞘链的目标.与F相关的领导者的更新位置的方式为：

其中：l是当前迭代次数，L是迭代的最大次数.

根据牛顿运动定律，跟随者xs的位置更新方式为：

由于优化的时间是迭代t，迭代之间的差异为1，在v0=0时，方程(3)变为：

2 预测模型

2.1 加权平均樽海鞘群算法

在SSA中，第i个跟随者的位置更新方式定义为方程（4），为第i个跟随者和第i-1个跟随者的位置的平均值，这可能导致樽海鞘链中前i个跟随者对第i个跟随者的影响不大.为此，将樽海鞘链中第i个跟随者的位置更新改进为前i个跟随者的加权平均，即：

其中：c1与方程（2）中的定义相同.我们将此改进称为加权平均SSA，记为AVSSA.

为验证所提算法AVSSA的有效性，选取了5个比较的优化算法：蚁狮优化器（ALO）、灰狼优化器（GWO）、飞蛾扑火优化（MFO）算法、鲸优化算法（WOA）和樽海鞘群算法（SSA）.本文所采用的23个基准函数F1(x)～F23(x)来源于文献[17]，其中：F1(x)～F7(x)为7个n维单峰函数，F8(x)～F13(x)为6个n维多峰函数，F14(x)～F23(x)为10个固定维数的基准函数.在Win10 64bit专业平台和64 GB RAM下Matlab R2019a工具箱下运行这6个算法.

在这6个可比较的算法中，种群大小为50，最大迭代次数T=500.每个可比较的算法独立运行30次.将这30次独立运行的每个算法所获得的全局最小值的平均值（Avg.）和标准差（Std.）作为评价算法的性能指标.

独立运行这6个算法30次，得到了23个基准函数的最小函数值的Avg.和Std.，如表1所示.部分基准函数的收敛曲线如图1所示.由图1可见，AVSSA有最好的收敛性能.由表1可知，利用AVSSA得到单峰函数F1(x)～F4(x)，F7(x)的Avg.分别为1.18×10−145、1.61×10−73、2.66×10−145、1.15×10−73和5.81×10−5，这些都最接近全局最小值0，而AVSSA和SSA在函数F6(x)上有相近的Avg..AVSSA在多峰函数F9(x)和F11(x)上的Avg.达到全局最小值0，在函数F7(x)、F10(x)和F12(x)的Avg.分别是5.81×10−5、8.88×10−16和4.40×10−3，这些都最接近全局最小值0，且在多峰函数F13(x)上的Avg.与其它可比较的算法具有相同的数量级.对于固定维数的函数F16(x)～F19(x)，所有可比较的算法AVSSA、SSA、ALO、GWO、MFO和WOA都达到了全局最小值-1.031 6、3、0.398和-3.86，但AVSSA有最小的Std..对于固定维数的函数F22(x)，AVSSA得到了最小的Avg.-8.326 6，最接近于全局最小值-10.402 8.

图1 部分基准函数的收敛曲线

表1 23个基准函数的Avg.和Std.

基于上述分析和讨论，所提出的算法AVSSA优于其它可比较的算法SSA、ALO、GWO、MFO和WOA，更适于基准函数的极值寻优.

2.2 基于AVSSA和BP神经网络的预测模型

利用所提出的AVSSA优化有一个隐含层的BP神经网络的参数：输入层与隐含层的连接权值W，隐含层与输出层的连接层的连接权值W′，隐含层的偏差b和输出层的偏差b′.将此预测模型记为AVSSA-BP，具体步骤为：

步骤1：初始化.初始化的参数包括樽海鞘链中樽海鞘的大小、最大迭代次数、隐含层中神经元节点的个数、终止条件.

步骤2：将链中的每个樽海鞘映射为连接权值W和W′，偏差b和b′.选取函数

作为AVSSA的适应度函数，其中Q是样本数，yis和分别是第s个样本的预测输出和目标输出.

步骤3：执行AVSSA算法，利用公式（1）和（5）分别更新链中领导者和跟随者的位置.

步骤4：若满足终止条件，则返回AVSSA算法的食物源F，转向步骤5.否则执行AVSSA，转向步骤2.

步骤5：将食物源F映射为连接权值W和W′，偏差b和b′，训练和测试BP神经网络.

预测模型AVSSA-BP的流程图如图2所示.

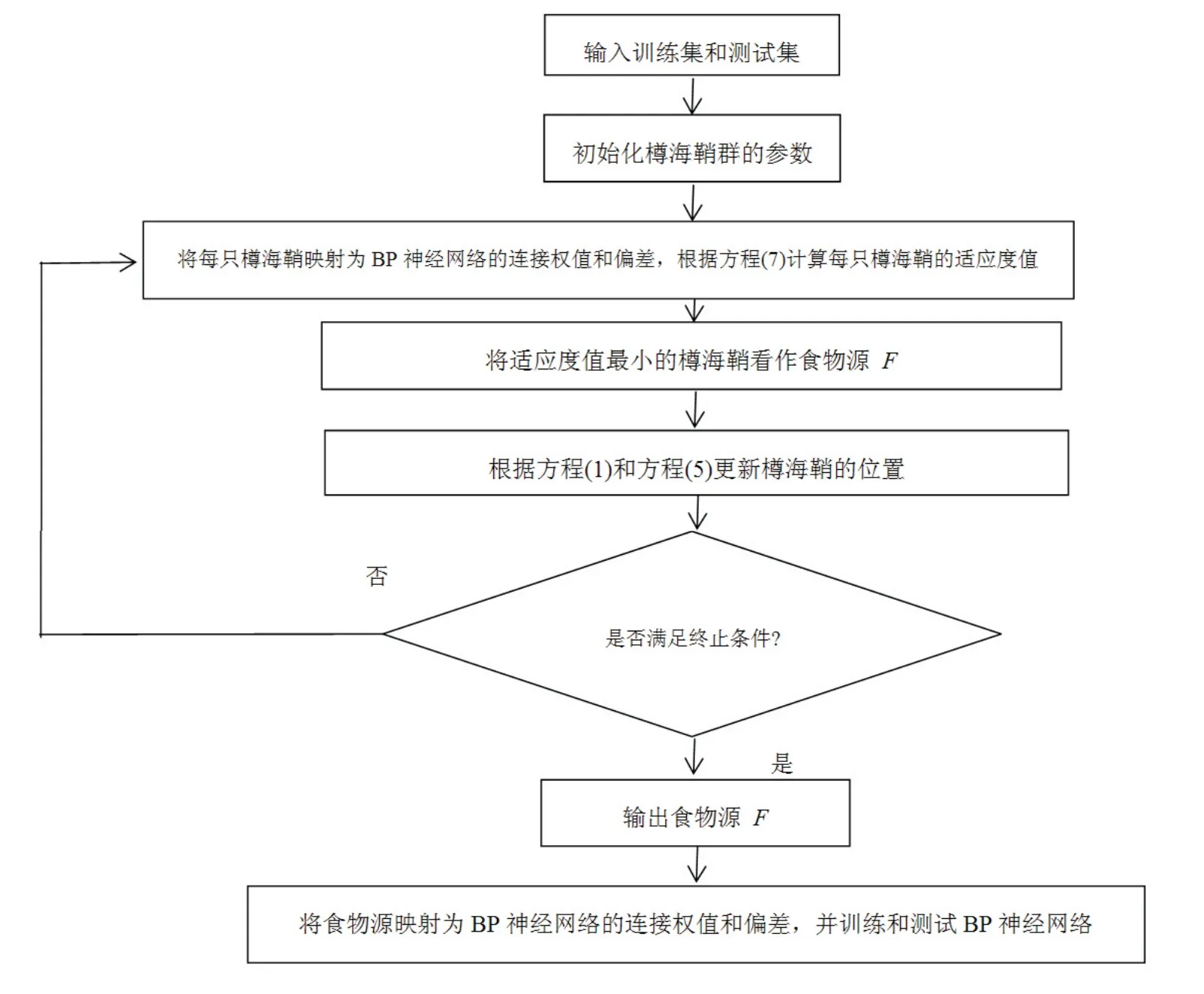
图2 AVSSA-BP模型的流程图

3 实验

3.1 数据源

本文所采用的COVID-19数据为2020年3月5日至2020年10月6日国家卫健委公布的境外输入COVID-19累计确诊病例数，网站为http://www.nhc.gov.cn/xcs/xxgzbd/gzbd-index.shtml.所采用的COVID-19数据利用前3天的COVID-19累计确诊病例数预测第4天的COVID-19累计确诊病例数.得到了214组3维输入数据，再删除最后一组3维数据，这样就得到了213组输入数据，将前192组数据作为训练数据，剩下的21组数据作为测试数据.

为验证AVSSA-BP的预测性能，我们仍然选取SSA、ALO、GWO、MFO和WOA优化BP神经网络的参数，建立预测模型SSA-BP、ALO-BP、GWO-BP、MFO-BP和WOA-BP进行比较，并与BP神经网络进行比较.

在本文中，平均绝对误差（Mean Absolute Error,MAE），根均方差误差（Root Mean Square Error,RMSE），平均绝对百分比误差（Mean Absolute Percentage Error,MAPE）和确定性系数R2[16]作为预测模型AVSSA-BP的评价指标.

3.2 实验结果

在预测模型AVSSA-BP的BP神经网络中，输入层神经元的个数为3，输出层的节点个数为1.经过大量的实验，选取预测模型AVSSA-BP中BP神经网络的隐含层的神经元节点数为6.这样我们将AVSSA-BP中樽海鞘链的每个樽海鞘映射为输入层与隐含层之间的连接权值W，隐含层与输出层之间的连接权值W′，隐含层的偏差b和输出层的偏差b′，这样预测模型AVSSA-BP中樽海鞘链的每个樽海鞘的维数为3×6+6×1+6+1=31，并选择方程（7）作为AVSSA的适应度函数.

在实验中，AVSSA-BP、SSA-BP、ALO-BP、GWO-BP、MFO-BP和WOA-BP的种群大小为50，最大迭代次数为100.独立运行BP神经网络，AVSSA-BP、SSA-BP、ALO-BP、GWO-BP、MFO-BP、WOA-BP和BP各30次，得到7个预测模型AVSSA-BP、SSA-BP、ALO-BP、GWO-BP、MFO-BP、WOA-BP和BP的21个测试样本的预测值的平均值和评价指标，分别见表2和表3.

表2 测试数据的预测值

表3 测试数据的评价指标

由表3可知，利用AVSSA-BP得到的境外输入病例确诊的COVID-19累计病例数预测的平均MAE、RMSE和MAPE最小，分别为4.311 0、1.413 4和0.154 7，且具有最高的平均确定性系数.因此，预测模型AVSSA-BP优于其它预测模型SSA-BP、ALO-BP、GWO-BP、MFO-BP、WOA-BP和BP.实验结果表明AVSSA算法能有效地优化神经网络的参数实现COVID-19的预测.

4 讨论与结论

本文对SSA中樽海鞘链中第i个跟随者的位置更新进行了改进，得到加权平均的SSA，记为AVSSA.将AVSSA与BP神经网络相结合，对境外输入确诊COVID-19累计病例建立了预测模型AVSSA-BP，且AVSSA-BP具有最小的预测误差MSE、MAE、RMSE和MAPE，最高的确定性系数R2.实验结果表明AVSSA-BP优于SSA-BP、ALOBP、GWO-BP、MFO-BP、WOA-BP和BP模型.

在以后的研究中，我们还可以对SSA算法进行改进，并将其与其他一种或多种群智能算法相结合，建立新的混合算法来提高其性能.这些新算法可以用来优化某些机器学习算法的参数，以解决预测和分类问题.