Bounds on Two Distance-Based Invariants Proximity and Remoteness in Terms of Minimum and Maximum Degrees∗

ZHANG Wanping,MENG Jixiang,QIAO Hongwei

(School of Mathematics and System Sciences,Xinjiang University,Urumqi Xinjiang 830017,China)

Abstract: The proximity π(G)and the remoteness ρ(G)are minimum and maximum average distance from a vertex v to all other vertices in G,respectively.Similar to the Wiener index,the proximity π(G)and the remoteness ρ(G)are also two distancebased invariants.The Wiener index reveals the global-property of graphs while the proximity π(G)and the remoteness ρ(G)point out the local-property.In this paper,we give some upper bounds on the π(G)and the ρ(G)in terms of minimum degree,maximum degree and girth in a triangle-free or a C4-free graph.

Key words: proximity;remoteness;minimum degree;maximum degree;girth;packing

0 Introduction

All graphs considered in this paper are finite,simple and connected.LetG=(V,E)be a simple and connected graph,with vertex setVand edge setE.Let|V|=n,|E|=m.The eccentricitye(v)of a vertersvinGis the largest distance fromvto another vertex ofG.Denote radius,diameter,and average eccentricity byr,Dandecc,respectively.That is

A vertexvinGis called a centre vertex ife(v)=r(G).The transmission σ(v)of a vertexvis the sum of the distances fromvto all others.The proximity π(G)and the remoteness ρ(G)are minv∈V{(v)}and maxv∈V{(v)}.That is,if we denote(v)as the average distance from a vertexvto all other vertices inG,we have

The Wiener indexW(G)of a graphGis the sum of distances between each pair of vertices,that is,

The Wiener index was proposed by Wiener Harold[1]in 1947.Since then,the Wiener index has obtained wide attention and achieved splendid results.

Compare the definition of the Wiener index and the proximity(resp.remoteness),one can easily find out that the Wiener index reveals the global-property of graphs and proximity π(G)(resp.remoteness ρ(G))point out the local-property.

The transmission σ(v)of a vertexvwas introduced by Entringer,Jackson,and Snyder in[2],and studied by Polansky and Bonchev in[3].Zelinka[4]introduced a notion asm1(v)=,which is very close to the average distance from a vertex.

Ma,Wu,and Zhang[5]succeeded in proving a conjecture that consists of an upper bound onecc−π together with the corresponding extremal graphs.Wu and Zhang[6]proved two conjectures involving average distance,radius,and remoteness.

Aouchiche and Hansen[7]considered the Nordhaus-Gaddum relations for π and ρ,gave the lower and upper bounds on π⊕¯π and ρ⊕¯ρ,where ⊕denotes+,−,×,or÷.They also established some relations for girthgand proximity π(remoteness ρ,respectively)in[8].

In [9],Sedlar proved a series of AutoGraphiX conjectures in two of which remoteness ρ is involved.Hua and Das[10]proved two AutoGraphiX conjectures involving remoteness ρ and proximity π in graphs.

The distance eigenvalues of a connected graph,denoted by ∂1,∂2,...,∂n,are those of its distance matrix,and are indexed such that ∂1≥∂2≥...≥∂n.Recently,Aouchiche and Hansen[11]gave lower and upper bounds on the distance spectral radius using proximity and remoteness,and lower bounds on ∂1−π and ∂1−ρ (∂1denotes the largest eigenvalue of its distance matrix).In addition,they formulated several conjectures which consist of lower bounds on ρ+∂3,.Lin,Das,Wu[12]proved two above-mentioned conjectures,that is,ρ+∂3>0 whenD≥3 and.Mojallal and Hansen[13]proved a stronger result than one of them,which is π+∂3>0 withD≥3.Jia and Song[14]considered the relations between remoteness and distance(signless)Laplacian eigenvalues.

Recently,Ai,Gerke,and Gutin[15]considered the lower and upper bounds on remoteness and proximity in digraphs.In[16],Pei,Pan and Wang solved some conjectures on the domination number,average eccentricity and proximity.Moreover,several authors turn their attention from graphs to digraphs(resp.networks).It is natural for us to consider the proximity and remoteness along this line.In[17],Zhang and Meng considered the restricted arc-connectivity of generalized De Bruijn digraphs and Kautz digraphs.In [18],Sun and Meng considered the vertex fault tolerance ofG(G0,G1;M) networks with respect to maximally connectivity.Zhu and Meng[19]considered the cycle-edge(resp.cycle-arc)connectivity of graphs.Some related results about the restricted connectivity of some networks can be found in[20]and[21].

In[22],Aouchiche and Hansen first proved upper and lower bounds on π and ρ as a function of the ordernofG,and gave the following sharp bounds on the proximity and the remoteness ofG:

Dankelmann[23]gave upper bounds on the proximity and the remoteness of a graph in terms of minimum degree δ and ordern.

Theorem 1[23]LetGbe a connected graph of ordernand minimum degree δ,where δ ≥2.Then

We consider whether those upper bounds of Theorem 1 on the proximity and the remoteness can be improved in terms of other graph invariants (minimum degree,maximum degree,and girth).We will use the similar method mentioned in[24]to establish those bounds and find the extremal graphs.In this paper,we will give some new bounds on proximity and remoteness in terms of minimum degree,maximum degree and girth in a triangle-free graph or aC4-free graph.

In order to find extremal graphs,we give a simple fact that will be used frequently in this paper.It is easy to see that the average distance from a vertex to all other vertices will decrease by adding an edge toG(G≇Kn).An immediate consequence follows as:

Proposition 1LetGbe a connected graph and letTbe a spanning tree ofG.Then

Our main results are the following theorems.Firstly,we consider the bounds of the proximity and remoteness in terms of minimum and maximum degree in a general graph.

Theorem 2LetGbe a connected graph withnvertices,minimum degree δ ≥2 and maximum degree Δ.Then,there exists a spanning treeTofGwith

Secondly,we consider the bounds of the proximity and remoteness in terms of minimum and maximum degree in a triangle-free graph.

Theorem 3LetGbe a connected triangle-free graph withnvertices,minimum degree δ ≥2 and maximum degree Δ.Then,there exists a spanning treeTofGwith

Thirdly,we consider the bounds of the proximity and remoteness in terms of minimum and maximum degree in aC4-free graph.

Theorem 4LetGbe a connectedC4-free graph withnvertices,minimum degree δ ≥2 and maximum degree Δ.Then,there exists a spanning treeTofGsuch that

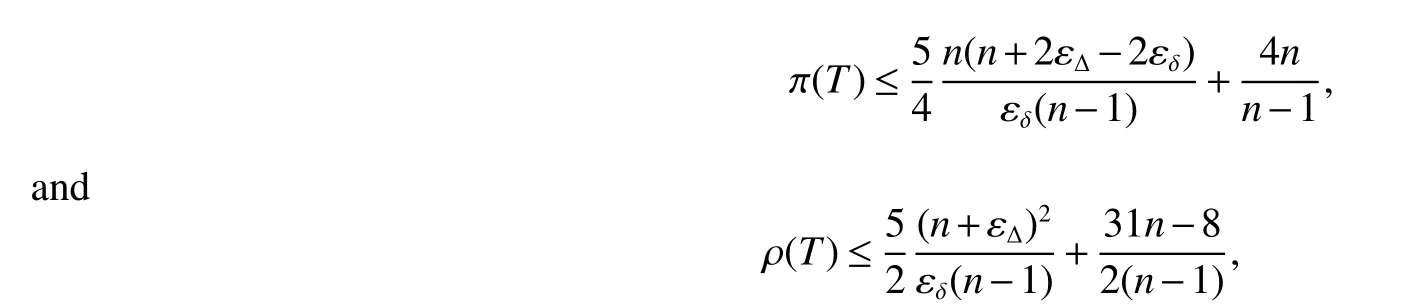
where εΔ=.

Finally,we consider the bounds of the proximity and remoteness in terms of minimum degree,maximum degree,and girth in a connected graph.

Theorem 5LetGbe a connected graph withnvertices,minimum degree δ ≥3,maximum degree Δ,and girthg.Then,there exists a spanning treeTofG.

(i)Ifgis odd,then

where ϕ=ϕ(Δ,δ,g)=1+[Δ(δ−1)(g−1)/2−Δ]/(δ−2),φ=φ(δ,g)=1+[δ(δ−1)(g−1)/2−δ]/(δ−2).

(ii)Ifgis even,then

1 Definitions,Notation and Preliminaries

LetGbe a connected graph with vertex setV(G),letkbe a posive integer and letAbe a subset ofV(G).Thekth neighbour set(A)ofAis the set of all verticesxofGwithdG(x,a)≤k,wheredG(x,a)denotes the distance inGbetweenxanda.IfA={v},we useNG(v)instead of(v),which is the neighbour set ofv.The closed neighbour setNG[v]ofvisNG(v)∪{v}.G[A]is the subgraph ofGinduced byA.

Thekth power of a simple graphG=(V,E)is the graphGkwhose vertex set isV,two distinct vertices being adjacent inGkif and only if their distance inGis at mostk.

A k-packing ofGis a subsetA⊆VwithdG(u,v)>kfor allu,v∈A.

Definition 1[24]For a weight functionc:V(G)−→N0,we define the weighted distance of a vertexvas

We use the convention for a subsetM⊆V(G),and writec(M)for ∑v∈M c(v).

Lemma 1[23]LetGbe a connected graph,letabe a positive integer,and letc:V(G)−→N0be a weight function such thatc(v)≥a for allv∈V(G).LetN:=c(V(G)).Ifv0is an arbitrary vertex ofG,then

and ifv0is a centre vertex ofG,then

2 Main Results

Proof of Theorem 2First,we construct a maximal 2-packing ofGby the following procedure.Letv1be a vertex ofGwithdegG(v1)=Δ.LetM1={v1}.If there exists a vertexv2inV(G)−M1withdG(v2,M1)=3,letM2=M1∪{v2}.If there exists a vertexv3inV(G)−M2withdG(v3,M2)=3,letM3=M2∪{v3}.We continue this procedure aftertsteps until there exists no vertexvinV(G)−Mtwhich satisfiesdG(v,Mt)=3.LetM:=Mt.LetT′be the forest with vertex set ∪u∈M N[u]and edge set all edges incident with a vertex inM.By our construction ofT′,there exist|M|−1 edges inG,each of them joining two components ofT′,and whose addition toT′yields a subtreeT′′ofG.ExtendT′′to a spanning treeTofG.For every vertexuofV(G),there exists a vertexuMinMsuch thatd(u,uM)≤2.Define a weight functionc1:V(T)→N by

It is easy to see thatc1(v1)≥Δ+1,andc1(u)≥δ+1 for each vertexu∈V(M)−{v1}.By a simple observation,we have∑v∈V(T)c1(v)=nand

Thus,we get

We consider two cases,depending on whetherv∈Morv∈V(T)−M.

Case 1v∈M.

We define a new functionc2arising from the functionc1by the following way

In order to bound σc1(v,T)in(2),we consider the graphT3[M].For allw∈M,dT(v,w)≤3dT3[M](v,w).We get

Note thatT3[M]is connected and|T3[M]|=|M|.We have

Now,we consider the bound ofdT3[M](v,v1),forv,v1∈T3[M].Clearly,dT3[M](v,v1)≤diam(T3[M])−1=|M|−1.By(1),we havedT3[M](v,v1)≤(n−Δ−1)/(δ+1).

Substituting this inequality into the above-obtained formula,we get

By the definition ofc2,one can findc2(u)≥δ+1 for each vertexu∈V(M),andN2=∑v∈V(T)c2(v)=n+δ−Δ.Hence,by Lemma 1 we have

Putting together(2)～(6),we obtain

Dividing both sides of the inequality(7)byn−1 yields

Inequality(8)shows thatTcontains a vertexvby δ ≥2,after division byn−1,we have

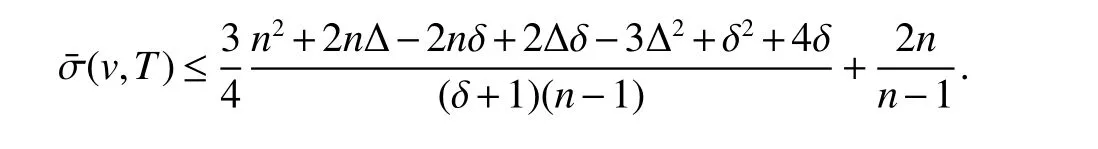
Case 2v∈V(T)−M.

By definition ofM,we can readily find that there exists a vertexvM∈M,such thatdT(v,vM)≤2,for every vertexvofV(T).Since for every vertexw∈V(T)−{v,vM},|dT(v,w)−dT(vM,w)|≤2,we have

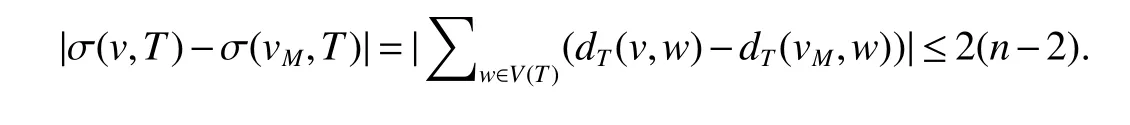
Hence,we get

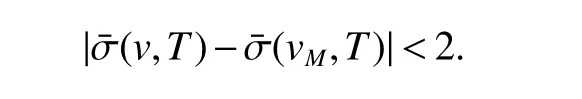
In conjunction with(7)we obtain

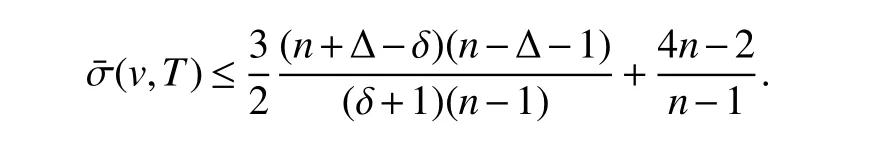
Corollary 1LetGbe a connected graph withnvertices,minimum degree δ ≥2 and maximum degree Δ.Then

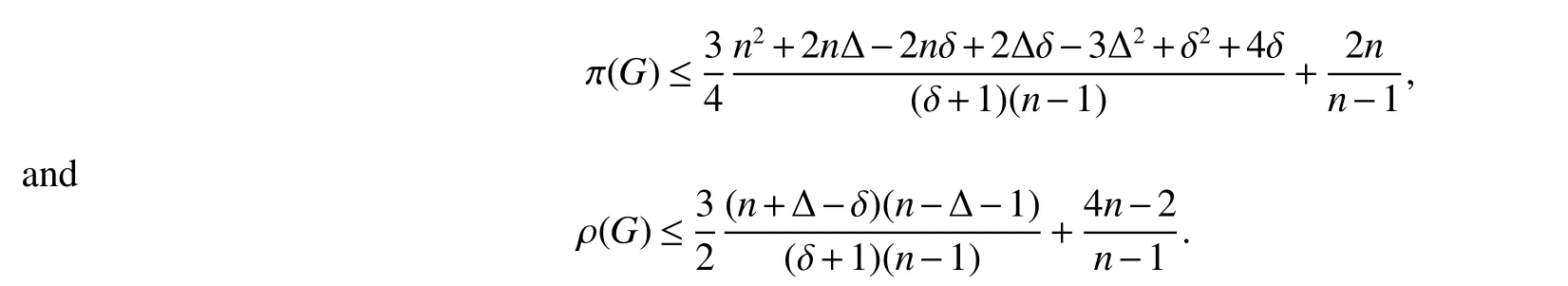
ProofThe results immediately follow by Theorem 2 and Proposition 1.

The graph constructed in the following example shows that the bounds in Theorem 2 and Corollary 1 are best possible,apart from the value of the additive constant.For a vertexvof a connected graphG,the transmission σ(v)of a vertexvis the sum of the distances fromvto all others.Let σmin(G)=minv∈V(G)σ(v),σmax(G)=maxv∈V(G)σ(v).

Example 1For fixed Δ,δ,k∈N with δ ≥2 andkeven letGΔ,δ,k(see Fig1)be obtained by the following way,V(GΔ,δ,k)=,where

Fig1 GΔ,δ,k with Δ=7,δ=4 and k=2

E(GΔ,δ,k)={uv|u∈Vi,v∈Vj,|j−i|≤1}.It is easy to see thatn(GΔ,δ,k)=(k−1)(δ+1)+2(Δ+1),and that

Sincen=(k−1)(δ+1)+2(Δ+1),we have(k−1)(δ+1)=n−2(Δ+1)and.Bring these terms into above two formulas,we get

For an edge ofG,S(e)denotes the double-star which is a special subtree induced by endpoints ofeand its neighbours.Proof of Theorem 3Our target is to find a spanning treeTofGusing the following procedure.First we obtain a matchingMofG,letV(M)be the set of vertices incident with an edge ofM.Letv0be a vertex ofGwithdegG(v0)=Δ ande1incident withv0.LetM1={e1}andT1=S(e1),lete2be an edge at distance exactly 3 fromM1,d(e2,M1)=3,if such an edgee2exists.LetM2=M1∪{e2}and letT2be the graph obtained fromT1∪S(e2)by adding an edge joining a vertex ofS(e2).Lete3be an edge at distance exactly 3 fromM2,if one exists.Then there exists an edgefjoining some vertex ofT2and some vertex ofS(a3).LetM3=M2∪{e3}and letT3be the graph obtained fromT2∪S(e3)by adding the edgefmentioned above.Generally,givenMiandTi,we choose an edgeei+1at distance exactly 3 fromMi,if one exists,letfibe an edge joining a vertex inTito a vertex inS(ei+1),letMi+1=Mi∪{ei+1},and letTi+1be the graph obtained fromTi∪S(ei+1)by adding the edgefi.Repeat this proceduretsteps until all vertices are at distance at most 2 fromMt.M:=Mt,T0:=Ti.Clearly,T0is a tree and all vertices inV(G)−V(T0)are at distance at most 3 fromM.

ExtendT0to a spanning treeTofGand define a weight functionc1onV(T).

For every vertexu,there exists a vertexuMinM,such thatd(u,uM)≤3.Define the weight functionc1:V(T)→N by

By the definition ofc1,we have

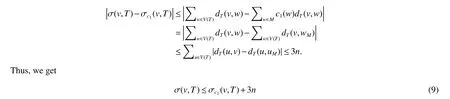
SinceGis triangle-free,N(u)∩N(v)=∅for each edgeuv∈E(G).Hence,degT(v0)=degG(v0) ≥Δ and degT(u)=degG(u)≥δ for each vertexu∈V(M)−{v0}.

By a simple observation,one can findc1(v0)≥Δ+1,andc1(u)≥δ+1 for each vertexu∈V(M)−{v0}.

Now we consider the line graphL(T)ofT,whose weight functionc2arises fromc1by the following way.Define the weight functionc2on the ling graphL=L(T)with vertex setV(L)=E(T)as following.

c2(uv)=c1(u)+c1(v),ifuandvbelong toM.Otherwisec2(uv)=0.

Then

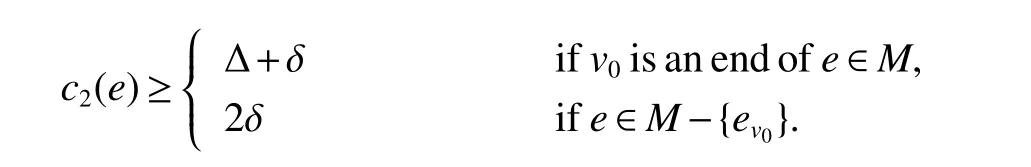
By a simple observation,we have ∑wu∈M c2(wu)=∑v∈V(T)c1(v)=nand

Letu,vbe two vertices ofT.Leteuandevbe edges ofTincident withuandvrespectively.LetPbe the (u,v)−path inT.If,exactly one of edgeseuandevbelongs toE(P),thendT(u,v)=dL(T)(eu,ev).If none of them belongs toE(P),thendT(u,v)=dL(T)(eu,ev)−1.If both of them belong toE(P),thendT(u,v)=dL(T)(eu,ev)+1.

Thus

By the definition ofc2,d(u,uM)≤3 for every vertex ofuofT−M,we have

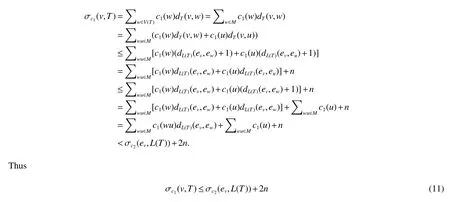
By our construction,there exist matching edgese1,e2∈M,such thatdT(e1,e2)=3.ThendL(T)(e1,e2)≤4.

Next,we consider the induced subgraphL4[M].It is easy to see thatL4[M]is connected and

Now,we define a new weight functionc3arising from the functionc2by the following way

Thenc3(e)≥2δ,for eache∈M.N3=∑ew∈M c3(ew)dT(ev,ew)=N2−Δ+δ=n−Δ+δ.For each edgeeofL4[M],we have

Note thatL4(M)is a connected subgraph ofL(T)with order|M|,thusdL4(M)(ev,e1)≤diam(L4(M))−1==.Then we deduce the following

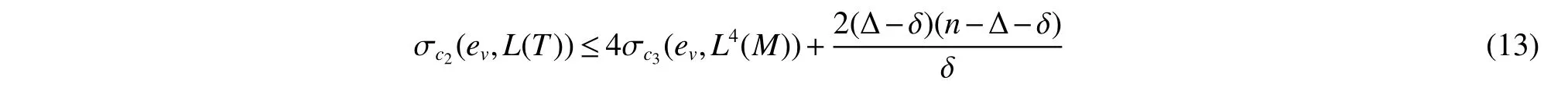
We consider two cases,depending on whetherv∈Morv∈V(T)−M.

Case 1v∈M.

Sincec3(e)≥2δ for eache∈MandN3=n−Δ+δ.By Lemma 1,we get

After division byn−1,the formula(16)shows that for allv∈M

The formula(17)shows thatTcontains a vertexvby δ ≥2,after division byn−1,we have

Case 2v∈V(T)−M.

By definition ofM,we see that there exists a vertexvM∈M,such thatdT(v,vM)≤3,for every vertexvofV(T).Since for every vertexw∈V(T)−{v,vM},|dT(v,w)−dT(vM,w)|≤3,we have

Corollary 2LetGbe a connected triangle-free graph withnvertices,minimum degree δ ≥2 and maximum degree Δ.Then,

The following example shows that the bounds on the remoteness and proximity in Corollary 2 are the best possible apart from a termO(1).

Example 2For fixed Δ,δ,k∈N with δ ≥2 andkodd,let(see Fig2)be obtained by the following way,,where

Fig2 with Δ=8,δ=4 and k=7

Sincen=2kδ+2(Δ−δ),we havekδ=(n−2(Δ−δ))/2 andk=.Bring these terms into above two formulas,we get

Proof of Theorem 4We first obtain a maximal 4-packing ofGby the following procedure.Letv1be a vertex ofGwithdegG(v1)=Δ.LetM1={v1}.If there exists a vertexv2inV(G)−M1withdG(v2,M1)=5,letM2=M1∪{v2}.If there exists a vertexv3inV(G)−M2withdG(v3,M2)=5,letM3=M2∪{v3}.We continue this procedure aftertsteps until there exists no vertexvinV(G)−Mtwhich satisfiesdG(v,Mt)=5.LetM:=Mt.LetT′be the forest with vertex set ∪u∈M N[u]and edge set all edges incident with a vertex inM.By our construction ofT′,there exist|M|−1 edges inG,each of them joining two components ofT′,and whose addition toT′yields a subtreeT′′ofG.ExtendT′′to a spanning tree T of G.For every vertexuofV(G),there exists a vertexuMinMsuch thatd(u,uM)≤4.Define a weight functionc1:V(T)→N by

By a simple observation,we have ∑v∈V(T)c1(v)=nand

By the definition ofc1,we haved(u,uM)≤4 for every vertex ofu∈T−M.Thus,|dT(v,w)−dT(v,wM)|≤4,and

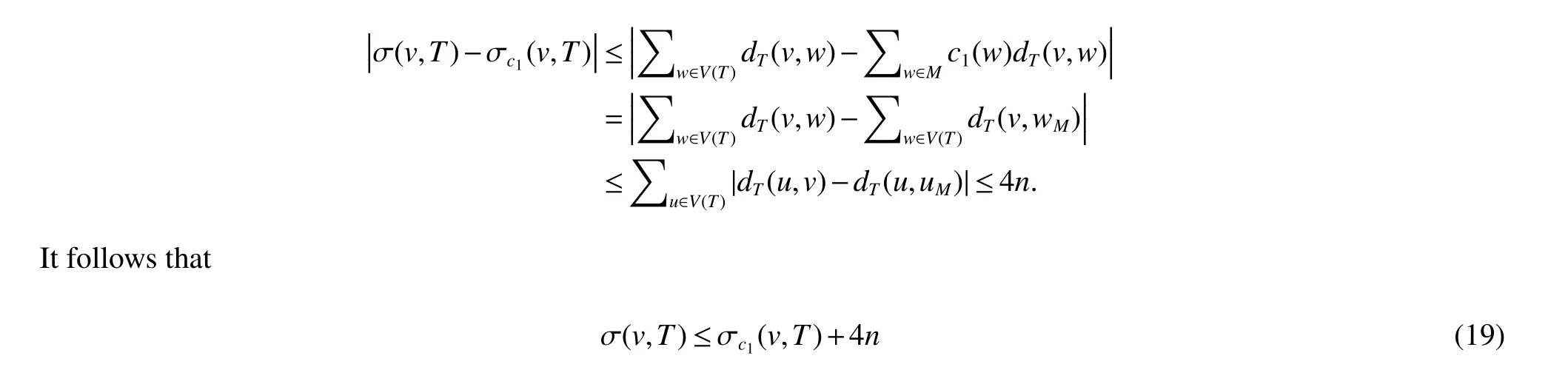
We consider two cases depending on whetherv∈Morv∈V(T)−M.

Case 1v∈M.

We define a new functionc2arising from the functionc1by the following way

In order to bound σc1(v,T)in(19),we consider the graphT5[M].Note thatT5[M]is connected,|T5[M]|=|M|and

Now,we consider the bound ofdT5[M](v,v1),forv,v1∈T5[M].Clearly,dT5[M](v,v1)≤diam(T5[M])−1=|M|−1.By(1),we havedT5[M](v,v1)≤(n−εΔ)/εδ.Substituting this inequality into the above formula,we get

By the definition ofc2,one can findc2(u)≥εδfor each vertexu∈V(M),andN2=∑v∈V(T)c2(v)=n+εδ−εΔ.Hence,by Lemma 1 we have

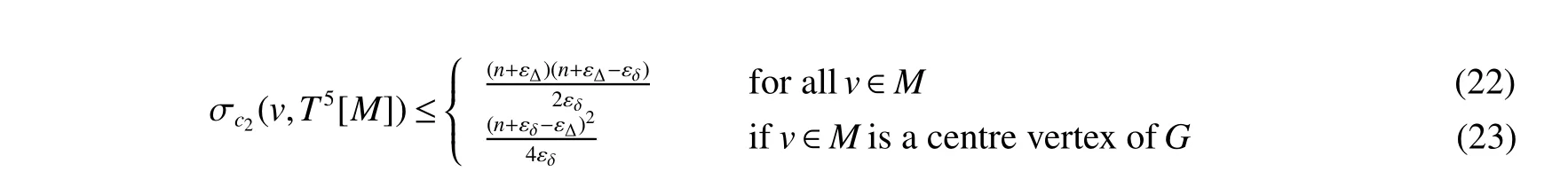
Combining(19)～(23),we obtain

The formula(24),after division byn−1,shows that for allv∈M

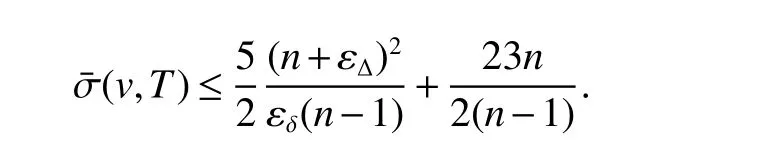
The formula(25)shows thatTcontains a vertexvby δ ≥2,after division byn−1,we have

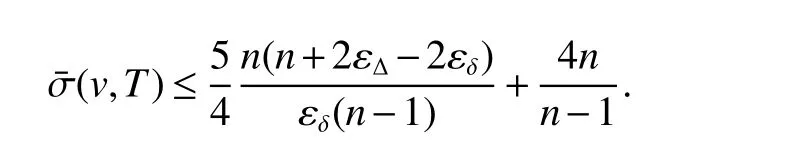
Case 2v∈V(T)−M.

By definition ofM,we can readily find that there exists a vertexvM∈M,such thatdT(v,vM)≤4,for every vertexvofV(T).Since for every vertexw∈V(T)−{v,vM},|dT(v,w)−dT(vM,w)|≤4,we have

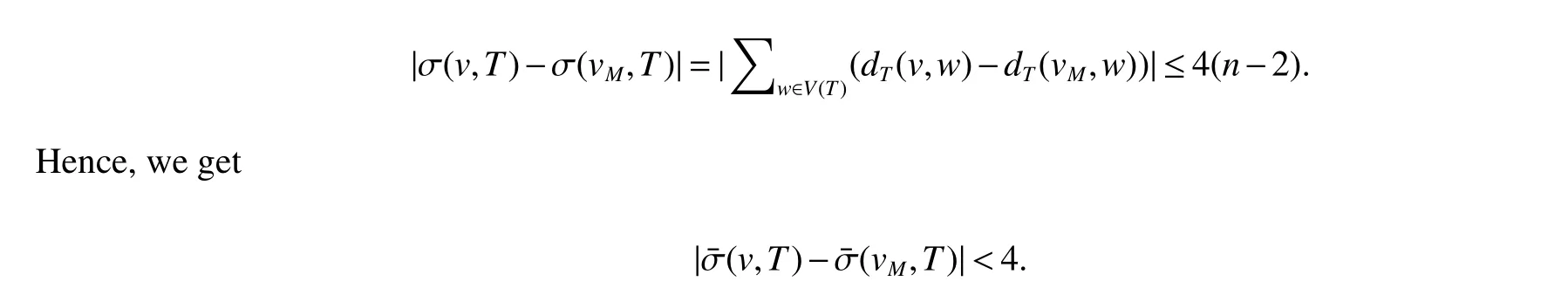
In conjunction with(25)we obtain

Corollary 3LetGbe a connectedC4-free graph withnvertices,minimum degree δ ≥2 and maximum degree Δ.Then,

where εΔ=.

The bounds of proximity and remoteness in Corollary 3 is not far from best possible.In[25],Erd¨os gave the following graph which satisfies the condition ofC4-free.

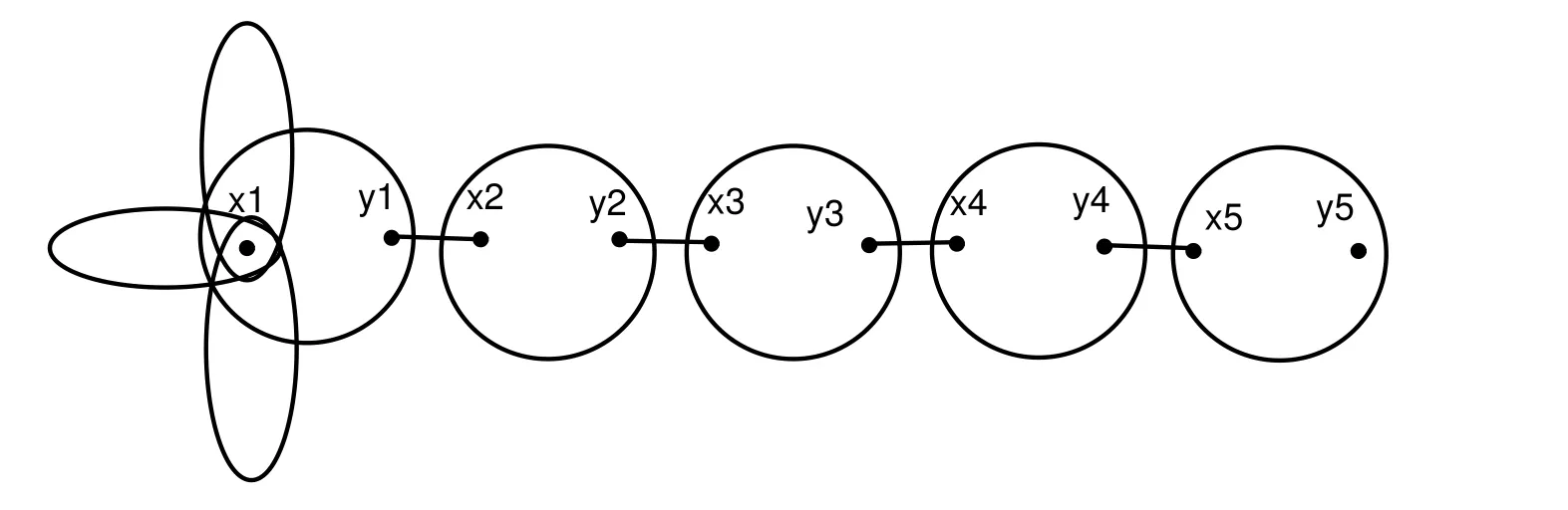
Fig3 with t=5, m=3,Δ=6q+5 and δ=q−1

We denote minimal number of vertices of a graph byn(g,δ) with girthgand minimum degree δ.An lower bound onn(g,δ)of a graph in terms of minimum degree δ and girthgwas given by Tutter in[26].

Lemma 2[26]

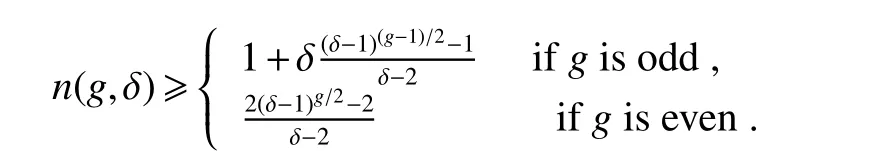
Equality holds for δ=3,g∈{3,4,5,6,8},andg=4,δ ≥3.

Proof of Theorem 5The proofs of(i)and(ii)are similar,so we only prove(i).Our target is to find a spanning treeTofGusing following method similar to the proof of the Theorem 1.5.First we obtain a maximal(g−1)-packingMofG.Letv1be a vertex ofGwith degG(v1)=Δ,and letM={v1}.If there exists a vertexv2inV(G)−M1withdG(v2,M1)=g,letM2=M1∪{v2}.If there exists a vertexv3inV(G)−M2withdG(v3,M2)=g,letM3=M2∪{v3}.We continue this procedure aftertsteps until there exists no vertexvinG−Mtwhich satisfiesdG(v,Mt)=g.For every vertexu,there exists a vertexuMinM,such thatd(u,uM)≤g−1.Define a weight functionc1:V(T)→N by

By the definition ofc1,we have

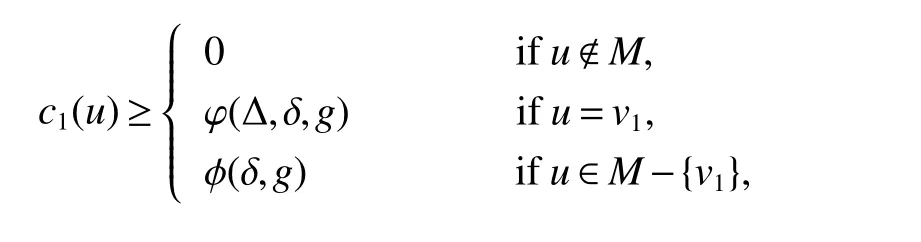
By a simple observation,we have ∑v∈V(T)c1(v)=nand

We denote ϕ(Δ,δ,g)(orφ(δ,g))by ϕ(orφ),respectively.

In order to bound σ(v,T),we consider the difference between σ(v,T)and σc1(v,T)and make the difference as small as possible.

By the definition ofc1,for every vertexuinT−M,there existsuM∈Msuch thatd(u,uM)≤g−1.By a similar proof to that of Theorem 4,we have

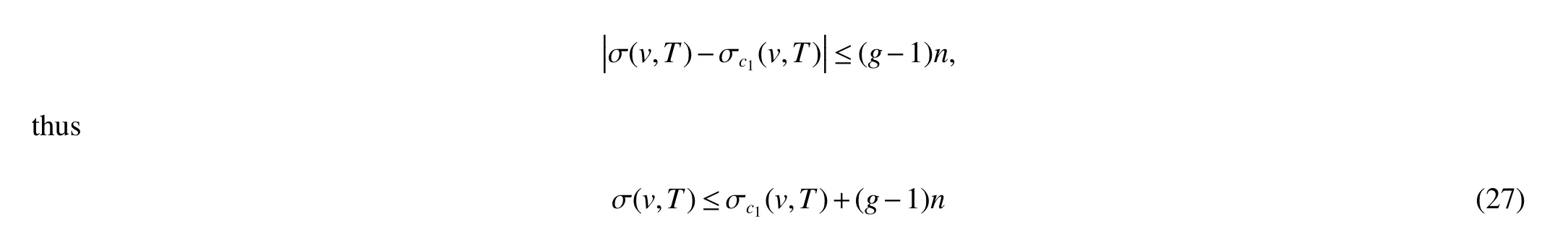
We only consider the case forv∈M.The proof of the other case forv∈V(T)−Mis similar.

We define a new functionc2arising from the functionc1by the following way

In order to bound σc1(v,T)in(27),we consider the graphTg[M].Clearly,Tg[M]is connected and|Tg[M]|=|M|.Thus,by(26),we havedTg[M](v,v1)≤diam(Tg[M])−1=|M|−1 ≤(n−ϕ)/φ.On the other hand,

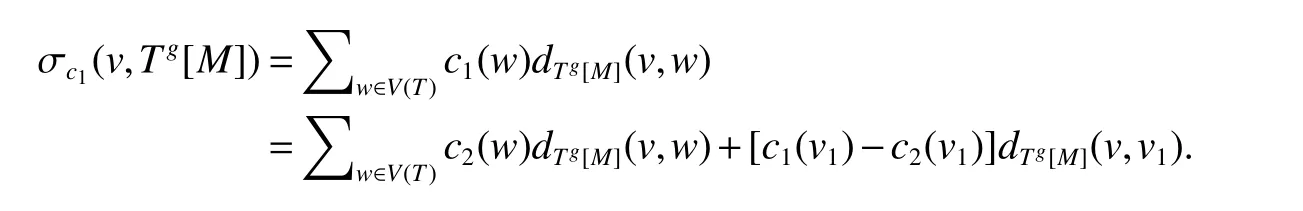
By a similar arguments to those of Theorem 4,(i)is established.

Corollary 4LetGbe a connectedC4-free graph withnvertices,minimum degree δ ≥2 and maximum degree Δ.Then,

(1)Ifgis odd,then

where ϕ=ϕ(Δ,δ,g)=1+[Δ(δ−1)(g−1)/2−Δ]/(δ−2),φ=φ(δ,g)=1+[δ(δ−1)(g−1)/2−δ]/(δ−2).

(2)Ifgis even,then

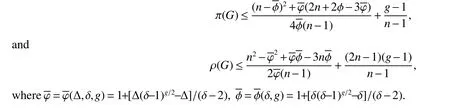
3 Concluding Remark

In this paper,we determine some new bounds on proximity and remoteness in terms of minimum degree,maximum degree and girth in a triangle-free graph or aC4-free graph.