The adaptive distributed learning based on homomorphic encryption and blockchain①

YANG Ruizhe(杨睿哲),ZHAO Xuehui,ZHANG Yanhua②,SI Pengbo,TENG Yinglei

(*Faculty of Information Technology,Beijing University of Technology,Beijing 100124,P.R.China)

(**School of Electronic Engineering,Beijing University of Posts and Telecommunications,Beijing 100876,P.R.China)

Abstract

Key words:blockchain,distributed machine learning(DML),privacy,security

0 Introduction

Today,people and Internet of Things are generating unprecedented amounts of data.Based on these data,machine learning as a data analytics tool learns from data,recognizes patterns,and makes decisions,becoming an important part of artificial intelligence(AI).However,collecting abundant data to the central server is usually expensive and time consuming,or even impossible due to privacy and security issues.Therefore,distributed machine learning(DML)as an alternative approach has attracted more and more attention[1].DML allows the owner to retain the original data,compute and update the model parameter locally using its data,which is periodically transmitted to the central server.Subsequently,the central server updates the global model by aggregating the received local parameter.In this way,the privacy of the original data is protected,and also the huge cost of data collection is avoided.However,there are still cyber risks in the interaction and message transmission,and potential malicious attacks can still extract some of their data information.

In order to resist attacks and enhance privacy,differential privacy and cryptography technologies are introduced in the existing work.Differential privacy(DP)can protect the sensitive information by adding random noise,therefore,attackers cannot infer from the results of some random algorithms[2-3].However,this differential noise needs to be smaller than the random noise of the sample,otherwise it will adversely affect the accuracy and privacy of the learning model[4].On the other side,cryptography with a mechanism of encryption can also protect the confidentiality of sensitive data.Therein,secure multiparty computing(SMC)and homomorphic encryption(HE)are the two main technologies.Comparatively,HE processing the underlying plaintext data in encrypted form without decryption is less complicated.In the current studies[5-7],the solutions using partial homomorphic encryption to protect the privacy in DML are more effective than those based on SMC.Considering the efficiency,Ref.[8]proposed an HE-based batch encryption technology to solve the encryption and communication bottleneck problems.

In the DML system,another challenge is security.Ref.[9]analyzed the potential threats,including semi-honest and malicious internal and external attacks.Some researchers have proposed distributed learning systems based on blockchain[10-11].Blockchain is a representative paradigm of distributed control technology.It provides a peer-to-peer network that enables sensitive participants to communicate and collaborate in a secure manner without the need for a fully trusted third party or an authorized central node.Ref.[10]proposed a blockchain based decentralized learning system for medical data and utilized blockchain as an information exchange platform.Refs[12-14]presented blockchain based distributed learning processes to resist different threats.

Currently the attention to both privacy and security in DML has become a key issue,however,the problems of computation and energy consumption brought by sophisticated privacy protection technology have been ignored in the most existing work.Here,a valuable business model is considered,in which the computing party as the beneficiary hires participants to jointly learn a desired global model.Specifically,the computing party aggregates the local models of the data from participants,but doesn’t share the aggregated results with any participants,so that it owns the value of the model.Therefore,an adaptive distributed machine learning scheme based on blockchain and homomorphic encryption is proposed.First,the Paillier encryption algorithm is used in the linear regression mode,where the computing party issues the global ciphertext parameters,and the participants always make ciphertext updates,so that the privacy of both the data and the model are satisfied.Second,the blockchain is introduced to complete the privacy-protected distributed linear regression process,which ensures the integrity and correctness of the updating and the final results of the model.Finally and most importantly,the total energy consumption of the system are analyzed from the perspective of computation complexity and computation resources,based on which a joint optimization of the computation resources allocation and adaptive aggregation in the case of limited system energy is given.Analysis and simulation results show the efficiency of the scheme in terms of security,privacy and learning convergence.

1 System model

In this section,a distributed learning framework is proposed based on homomorphic encryption and blockchain,which can complete the trusted learning process of the model without leaking private information.

1.1 System overview

The system completes a secure and private distributed learning based on the blockchain network,as shown in Fig.1.The system model includes two roles:the participants owning their private data and the computing party having requirements of data analytics(commercial requirements,etc.).Therefore,the computing party initiates the collaboration with participants to derive a global model from their data.Since the local model parameters of each participant are sensitive information having certain commercial value for others,the partial homomorphic encryption algorithm Paillier is used to encrypt them providing privacy protection.Besides,these ciphertext model parameters are uploaded to the blockchain,and the underlying distributed consensus guarantees the data sharing of model parameters in a reliable manner,thereby improving the transparency and trace ability of the learning.

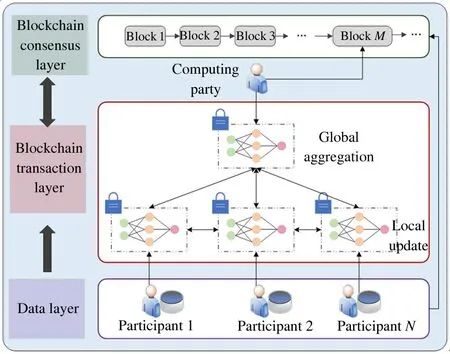
Fig.1 System model

Specifically,it is assumed that the data required by computing party is distributed among participants,then the system nodes composed of the participantsPand the computing partyCare denoted asI={P,C},|I|=N+1,where|·|represents size of sets.In the setP={P1,P2,…,PN},the elementPi(i∈1,2,…,N)represents the participant having a sub-data setDiand the total data set isD={D1,D2,…,DN}.

1.2 Distributed gradient descent

For simplicity,the distributed learning of linear regression model is concerned.For each data sample(xij,yij),the loss function can be expressed as

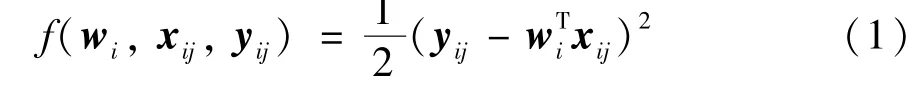
wherexijandyijrespectively denote thej-th input vector and output of datasetDi,andwiis the local parameter.Then the local loss function ofPibased on each datasetDiis

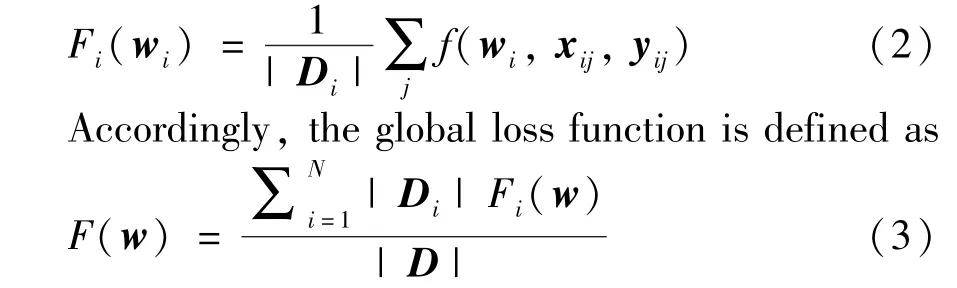
wherewis the global parameter.

During the learning process,t(t=1,2,…,T)is set as the number of iterations,andTis the total number of iterations.In each iteration,it contains a local update and a possible global aggregation.Whent=0,the local parameters of all participants are initialized to the same value.Whent＞0,the local modelwi(t)ofPiis computed according to the gradient descent(GD)rule based on its previous iteration.After certain local updates,the computing party performs global aggregation to derive a global model,which is a weighted average of the local models of all participants.

Therefore,the local update atPiusing gradient descent algorithm with local loss function can be described as

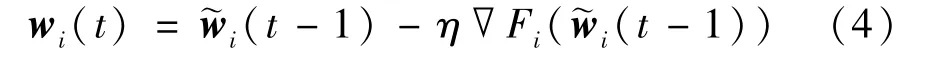
whereη＞0 is the learning rate.If global aggregation is performed by computing partyCat iterationt,the global model is defined as Eq.(5).

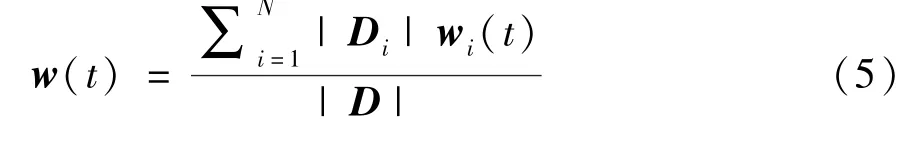
1.3 Learning based on blockchain and Paillier

It is defined that there areτlocal updates between every two global aggregation.It is assumed thatTis a multiple ofτ,andGis the total number of global aggregations,thenT=Gτ.

In a cryptographic system,the public keyPkis used for encryption and the private keySkis used for decryption.Here,[[·]]is used to represent the ciphertext message encrypted by Paillier.During the encrypted learning,the computing party owns the public key and the private key to obtain the global model,while the participants only hold the public key,so that the model parameters are only shared among the participants in the form of ciphertext,ensuring the privacy of the system model.

The encrypted learning process can be divided into model initialization,local update,and global aggregation.

(1)Model initialization.The computing party and participants as the blockchain nodes,form a pointto-point decentralized network.Before learning,the key pair(Pk,Sk)is generated,then all nodes agree on thePkand the hyperparameters of the learning model,such as the learning rate and the initial local ciphertext model,etc..

(2)Local update.In the ciphertext state,the participants use the gradient descent algorithm to update the local model in the current iteration based on the local ciphertext model completed in the previous iteration.During the encrypted updating,the participants compute local gradient using the homomorphic property[[am1+bm2]]=[[m1]]a·[[m2]]b.At iterationt,the local ciphertext gradient ofPican be written as

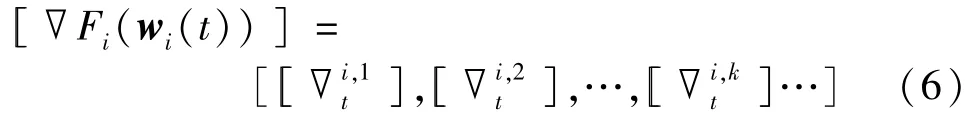
where[[∇i,kt]]is the ciphertext gradient of the local loss functionFi(wi(t))to thek-th element inwi(t)=[wi,1(t),wi,2(t),…,wi,k(t),…].Then[[∇]]can be derived as

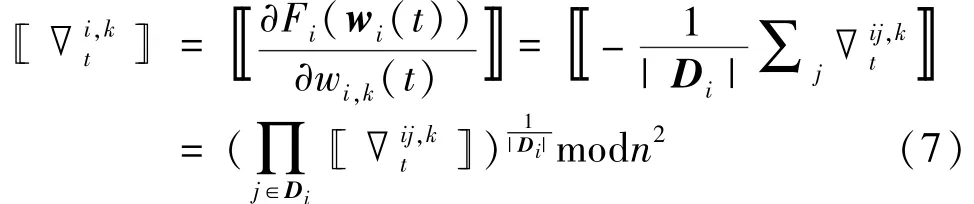
wherenis the parameter for the key[15],and[[∇ij,kt]]is the ciphertext gradient corresponding to samplexij,kand can be obtained by

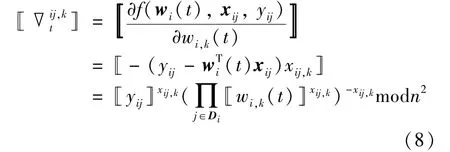
Based on the above theory and Eq.(4),the element[[wi,k(t)]]in the local ciphertext model ofPiat iterationtcan be expressed as

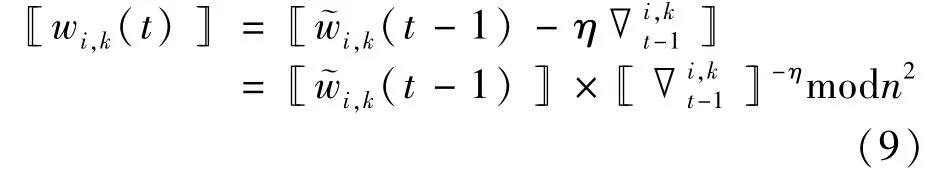
Using Eqs(8),(7)and(9),the participants can obtain[[wi(t)]].Afterτlocal updates,each participant encapsulates local ciphertext model into a transactionELWPi=(t,[[wi(t)]])and broadcasts it to other nodes.

(3)Global aggregation.The computing partyCperforms global aggregation afterτlocal updates.Specifically,the computing party collectsNtransactionsELWP1,…,ELWPNfrom the participants to obtain the local ciphertext model[[wi(t)]]at iterationt,and updates the global model in the encryption as

Then,the consensus based on PBFT protocol is performed.It is considered thatCas the primary node,and it is responsible to pack transactions containing the global ciphertext model and the received local ciphertext model into the new blockBg

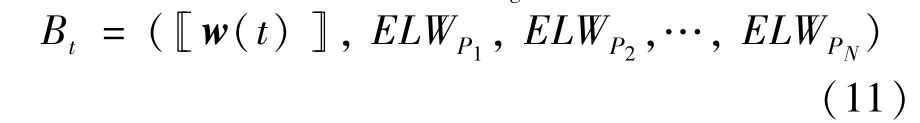
whereg=1,2,…,G;the number of blocks is the same as the number of global aggregations.As the replicas in the consensus,Piperforms verification,including the signature of each transaction,MAC,and the correctness of Eq.(10)according to the public key.

2 Joint optimization for computation resources and adaptive aggregation

The distributed learning,especially the computation and learning in encryption,will consume lots of computing and energy resources.For the computing partyCto obtain the value of its data analysis,it is necessary to keep operating costs low.Therefore,how to effectively use the given resources to optimize the learning effect(minimize the loss function)has become an important issue.To solve this problem,the computation cost and energy consumption at each node is analyzed,based on which the convergence performance of the model is improved by optimizing the computation resources allocation and the adaptive aggregation(dynamically adjust aggregation frequencyτ).

2.1 Resources consumption and analysis

For resources consumption,from the aspect of learning(including local learning and global learning)and the blockchain consensus respectively to analyze it,it is assumed that the computing resources used by nodei(i∈I)for learning and consensus are(CPU cycle frequency)and,respectively.(1)In learning(subsection 1.3),it is assumed that the average of the CPU cycles consumed by the participants and the computing party to complete a step of ciphertext calculation isμ1CPU cycles,and the average of the CPU cycles consumed to complete a step of plaintext calculation isμ2CPU cycles.

Local update.Pi'(i'∈I,i'=1,…,N)updates the local ciphertext model as shown in Eq.(9),and broadcasts it to the blockchain in the form ofELWPi'transaction.In this step,the computation complexity isO(|w||Di'|).Accordingly,the computation costsΔand computation timeεare

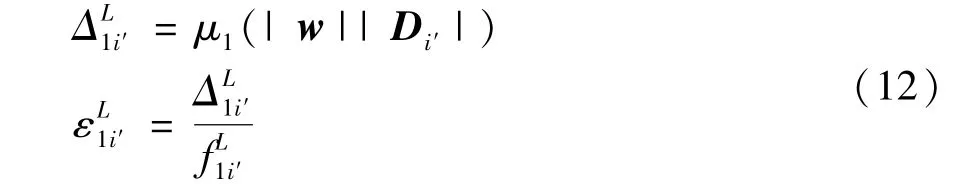
Global aggregation.The computing partyC(C=i″∈I,i″=N+1)collectsELWPi'fromPi',and updates the global ciphertext model as shown in Eq.(10).In this step,the computation complexity isO(N|w|).Since Paillier cannot handle the problem of ciphertext multiplication,the computing party needs to decrypt theELWPi'transaction,and computes the optimization parameterφ,δ(see subsection 2.2 for details).Its computation complexity isO(N|w||Di'|).The computation costsΔand computation timeεare

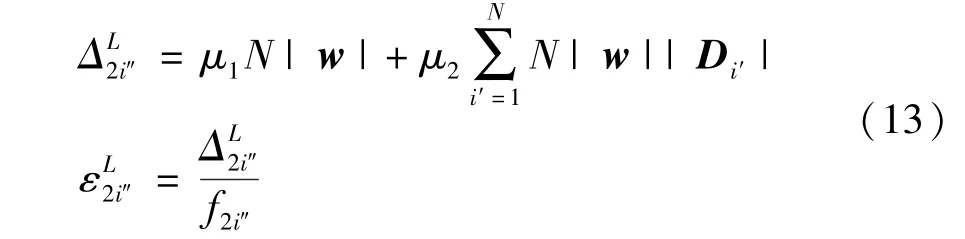
(2)In the PBFT consensus run between participants and the computing party,it can resist at mostF=3-1(N-1)failed nodes.It is assumed that the average value of the CPU cycles consumed by computing tasks isα,and generating or verifying a signature and generating or verifying a MAC requireβandθCPU cycles,respectively.The consensus protocol consists of five steps.

Step 1Request.Participants submitKtransactions containing model parameters to computing partyC(primary nodei″).The primary nodei″packs the verified transactions into a new block.Afterwards,it broadcasts the produced block and pre-prepare messagestoother nodes for verification.The computation costsΔand computationtimeεare

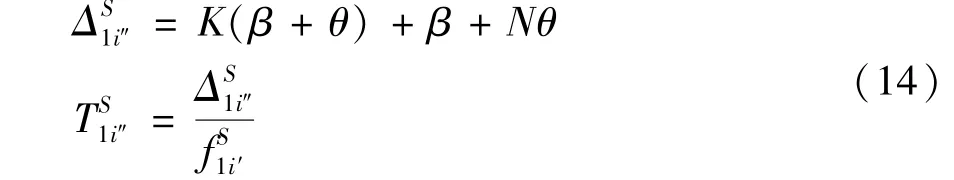
Step 2Pre-prepare.Pi'(i'≠i″)as replica receives a new block of pre-prepare message,then verifies the signature and MAC of the block and the signature and MAC of each transaction in turn.Finally,the computation result is verified according to the smart contract.If the result is verified successfully,Pi'will send the prepare messages to all the others.The computation costsΔand computation timeεare

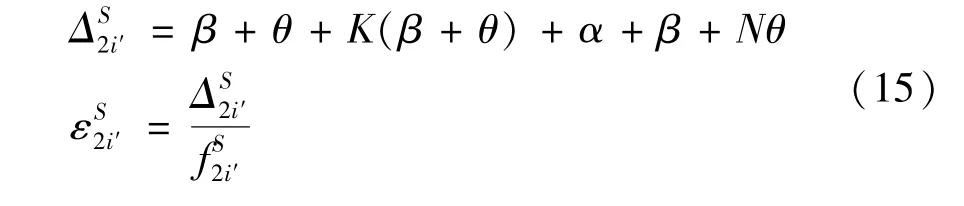
Step 3Prepare.All the nodes receive and check the prepare message to ensure that it is consistent with the pre-prepare message.Once the node receives 2Fprepare messages from others,it will send the commit messages to all the others.The computation costsΔand computation timeare

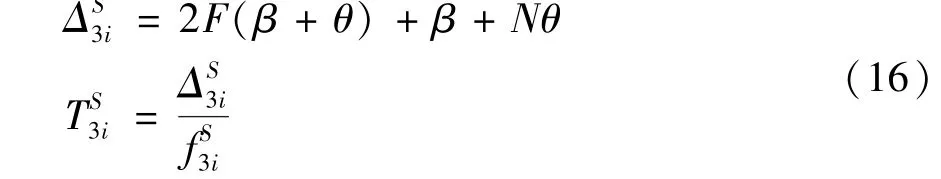
Step 4Commit.All the nodes receive and check the commit message to ensure that it is consistent with the prepare message.Once the node receives 2Fcommit messages from others,it will send the reply message to the primary node.The computation costsand computation timeare

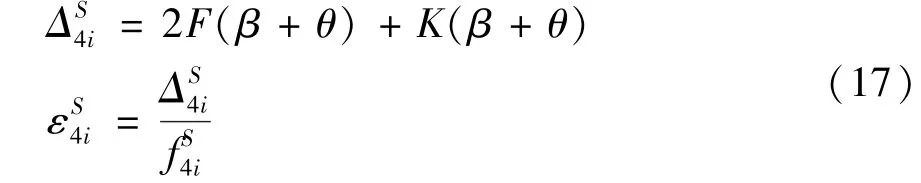
Step 5Reply.The primary node receives and checks the reply messages.After receiving 2Freply messages,the new block will take effect and be added to the blockchain.The computation costΔand computation timeare

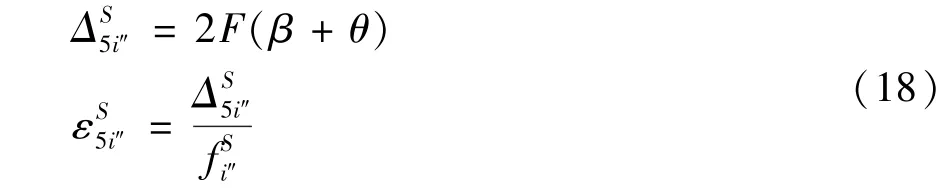
As analyzed above,the efficiency(computation time)of a node in each step is constrained by computation cost and computation resources.Following themodel in Ref.[14],the energy consumption of local update can be given as

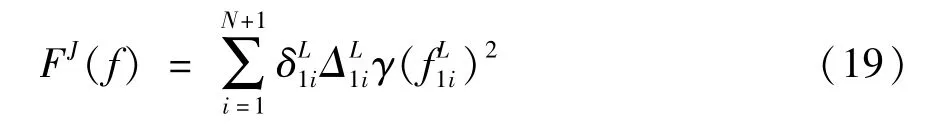
the energy consumption of global aggregation can be given as

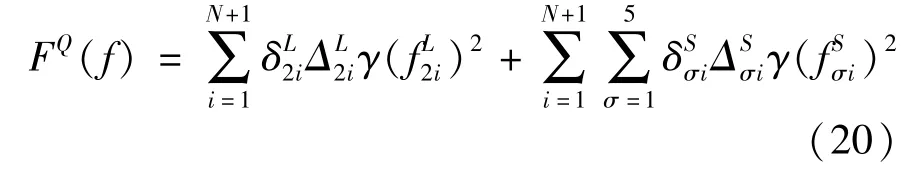
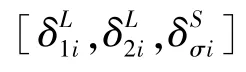
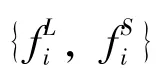
2.2 Optimization model and solutions

For the loss functionF(w),linear regression satisfies the following assumptions[16].Fi(w')andF(w)are convex,φ-smooth.For anyw,w'.‖∇Fi(w)-∇Fi(w')‖≤φ‖w-w'‖to capture the divergence between the gradient of a local loss function and the gradient of the global loss function.This divergence has to do with how data is distributed across different nodes,and the measure factorsφ,δwill affect the optimization model.For anyt,=∑i|Di|/|D|is defined to approximateφ,where

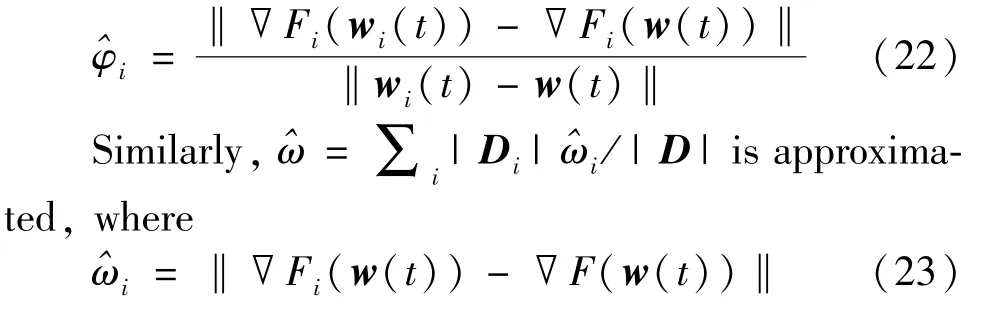
Therefore,the optimization model is defined as

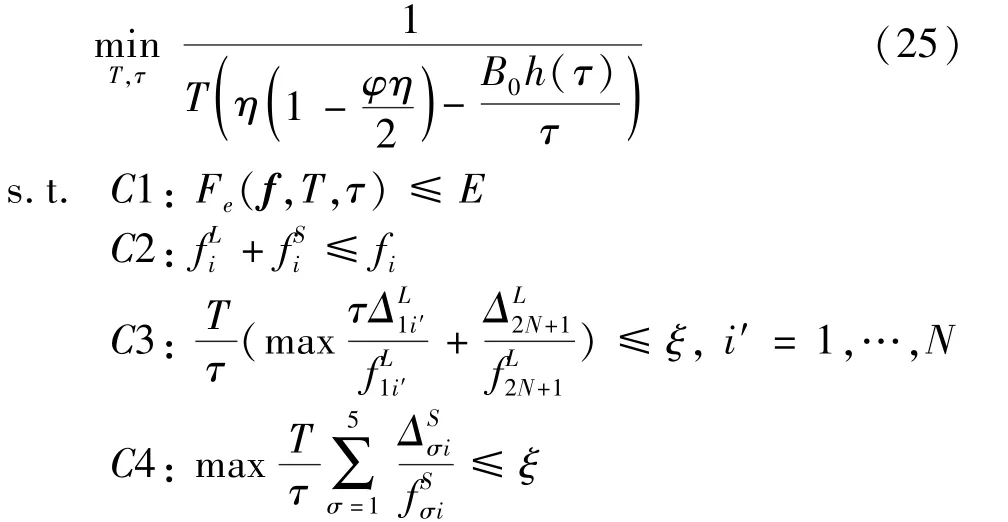
C5:τ≤τmax

where the loss function is minimized under the constraint ofC1-C5.The total system energyEis limited byC1,and the computation resources of the node is limited byC2.Moreover,the total time in the learning process and the consensus process are limited byC3 andC4,respectively,whereξmakes the time of the two processes consistent.Sinceτis unbounded and the problem is difficult to solve,the search space is restricted byτmaxinC5 and on integers.

Since the denominator of Eq.(25)is always positive,then combining Eq.(21)andC1,the parameterTcan be replaced by the optimal valueT=(Eτ)(τFJ(f)+FQ(f))-1.Note thatφandδin Eq.(25)are ideal values,and only the alternative approximated^φandδ^can be updated along the learning.In each global aggregation,the computation resources allocated for each node to complete each step and the aggregation frequencyτare optimized by the convex optimization theory.The joint optimization is repeated to decide the global aggregation until the energy of the system is consumed out,as shown in algorithm 1.

Algorithm 1 Process of learning and optimization Input:E,η,B0,ξ Output:[[w(T)]]1.Initial t=0,τ=1,R=0//R is the energy count 2.Initial E'=E and use Pk to obtain[[w(0)=0]]3.Initial f,evenly distributed to each process 4.while(t≥0＆E＞0)do 5. for i=1,2,3,…,N do 6. Pi downloads global parameter from blockchain 7.Pi completesτlocal updates 8. Pi broadcasts ELWPi 9. end for 10. t=t+τ 11. C receives[[wi(t)]]from Pi 12. C aggregates[[w(t)]]and calculates^δ,^φ 13. C calculates R=R+τFJ(f)+FQ(f)14. C updates E=E'-R 15. C uses Eq.(25)to obtain the optimal f andτ,whereτ∈[1,τmax]16. if R＞E'then 17. reduce toτthe maximum value within E'18. set E=0 19. end if 20. C creates a block and upload to blockchain 21.end while

3 Simulation and analysis

3.1 Security and privacy analysis

The system addresses data privacy and model security by combining distributed machine learning with homomorphic encryption and blockchain.

For privacy,the Palillier encryption algorithm is used to protect the model parameters,where the encrypted parameters prevent attackers from obtaining local data by eavesdropping on the broadcast and also protect every model parameter from other participants.Only the computing party as the sponsor can know the parameters.

For security,blockchain is used to make point-topoint interaction between computing party and participants to ensure the reliability of the system.Through the PBFT consensus,the participants are able to verify transactions and the updated ciphertext model from the beginning to the end results,which confirms the contribution of each participant.

3.2 Simulation

In this section,the proposed joint optimization scheme for computation resources and adaptive aggregation is simulated.To verify its performance,the proposed joint optimization is compared with the other two optimization cases using the loss function value as a metric.

Only-aggregation.Ref.[16]proposed an adaptive aggregation algorithm.Assuming that the computation resources are fixed(the computation resources allocated to each node in different steps are equal and fixed),only the aggregation frequency is adaptively optimized so that the loss function reaches minimum.

Only-resource.A comparison scheme for joint optimization,where the aggregation frequency is fixed,and only the allocation of computation resources is optimized.

In order to prove the generality of the joint optimization,it is validated on the Boston house price dataset with 14 features and the fish toxicity dataset with 7 features,respectively.506 pieces of sample data are selected on each dataset and all sample data are preprocessed to the interval[-1,1].80% of them are selected for training and others for testing.For simulations,the parameter settings are shown in Table 1.

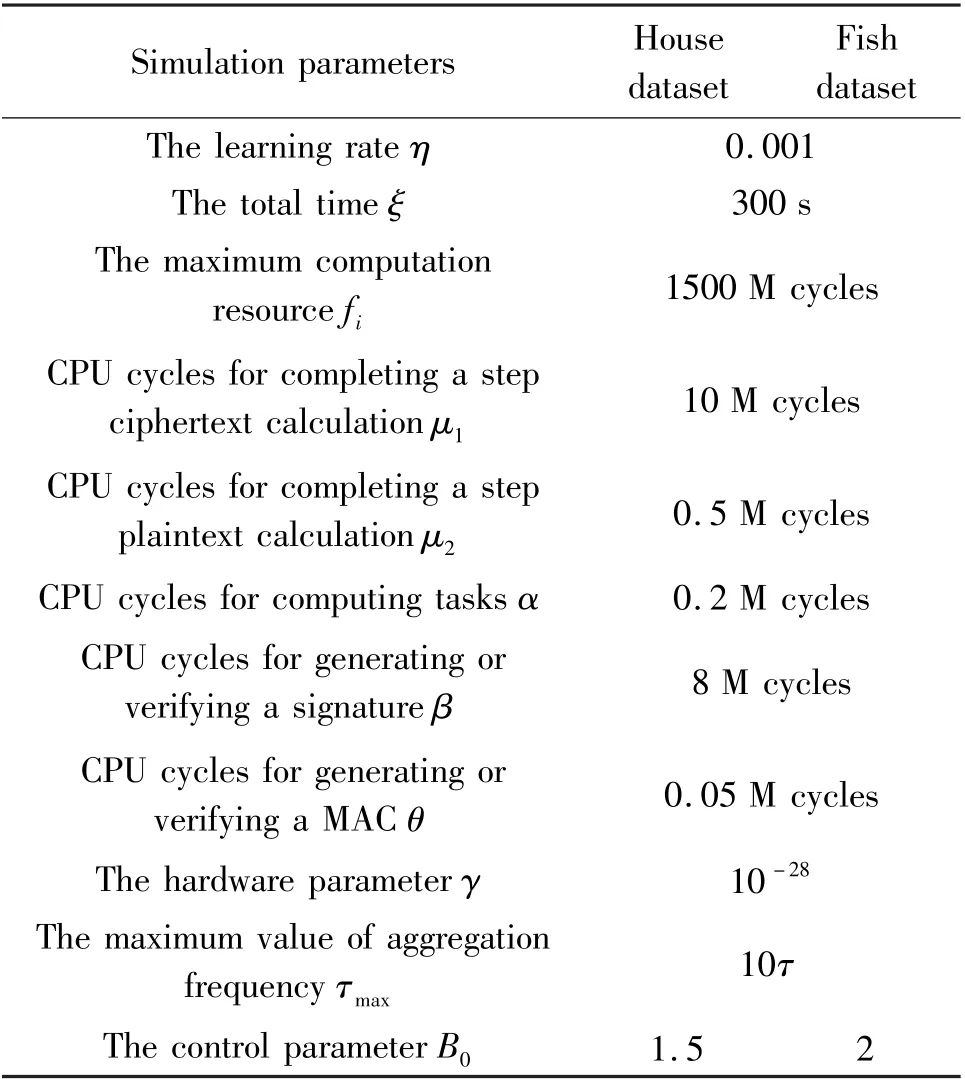
Table 1 The simulation parameters

Fig.2 and Fig.3 show the relationship between the loss value and the aggregation frequencyτ.In order to find the optimal fixedτin the only-resources optimization through simulations,it is considered that the value ofτis from 10 to 90.It can be seen that the optimal value ofτvaries with different number of participants and dataset,and a fixed value ofτwill not be suitable for all cases.Note that this optimal value can not be obtained in practical work.In order to facilitate comparison,according to the changing trend of the curve,τ=25 is set in the Boston dataset andτ=30 is set in the fish dataset.

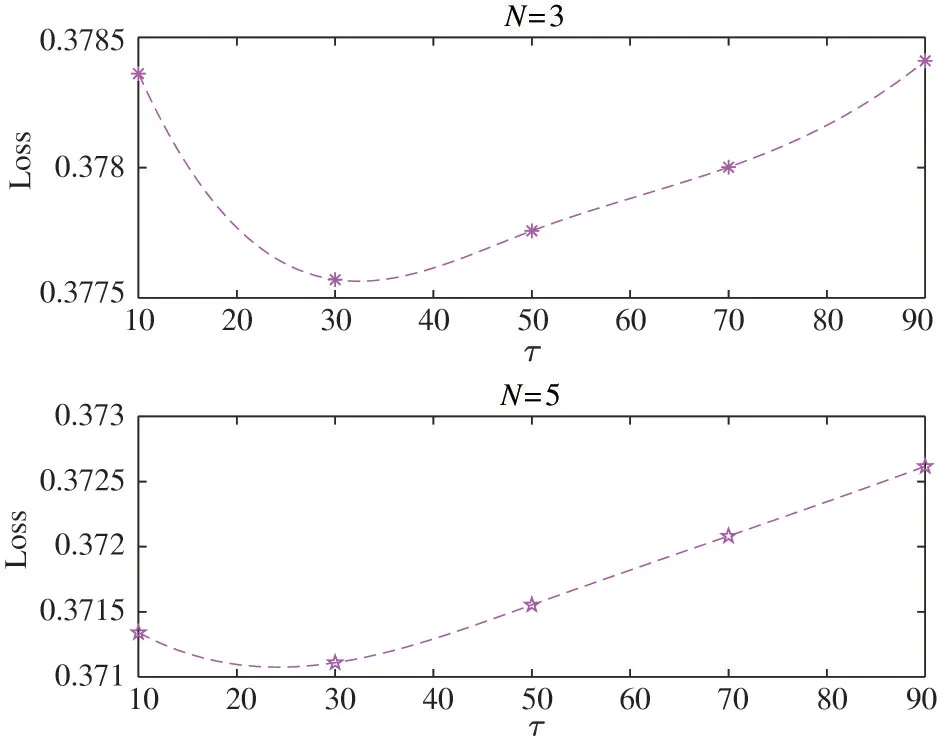
Fig.2 Loss value with differentτin Boston dataset

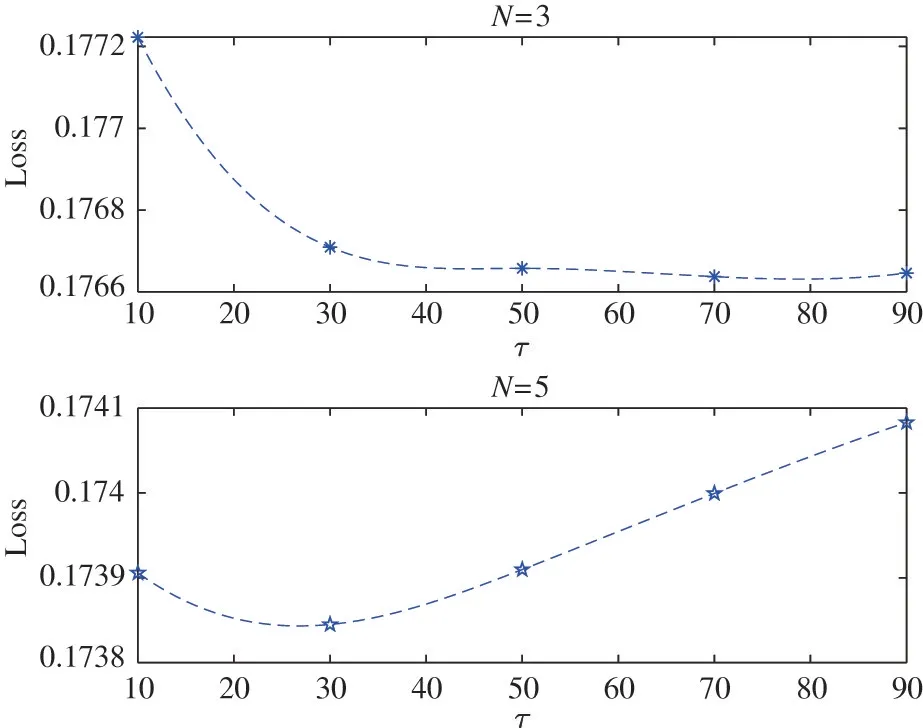
Fig.3 Loss value with differentτin fish dataset

Fig.4 shows the relationship between system energy and loss value when the number of participants isN=5.Since the Boston dataset has more feature dimensions than the fish dataset,it consumes more energy during learning and requires more energy to converge(i.e.different orders of magnitude on the horizontal axis).It can be seen that with the increase of the system energy,the loss values of the three cases decrease,and the joint optimization scheme has the smallest loss value.It adjusts the computation resources allocation of each node in each step according to the complexity,so that the energy consumption of each iteration reaches an ideal value and the distributed learning process can complete more iterations under the constraint of limited system energy.When the system energy is small,the effect of the joint optimization scheme is more obvious.In addition,there is a small difference between the loss value of joint optimization and only-resources optimization.It can be seen that in the distributed machine learning,optimizing computation resources allocation plays a more important role than optimizing aggregation frequency.

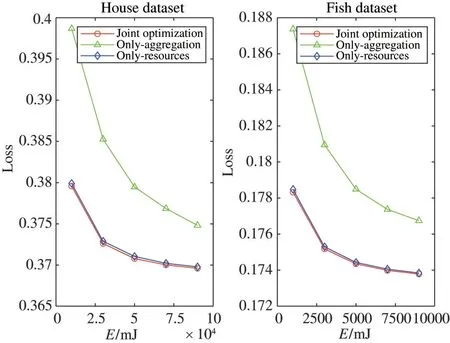
Fig.4 Loss value with different energy consumption

Fig.5 shows the relationship between the number of participants and the loss value.It can be seen that as the number of participants increases,the change trend of the loss value under different datasets is different.The reason is that the loss value is not only affected by the number of participants,but also related to the data distribution.With the same number of participants,the proposed joint optimization scheme has the smallest loss value.

4 Conclusions

A distributed learning scheme is proposed using homomorphic encryption and blockchain as the privacy and security guarantee.In the scheme,data is leaved to its owner and only the encrypted model parameters derived from data are transmitted to the global aggregation,all of which are recorded and verified by blockchain consensus.In this way,the privacy of both the data and model as well as the security of the learning are ensured.Most importantly,the computation resources and the adaptive aggregation in the distributed learning and consensus are optimized.Simulation results show the efficiency of the scheme.