Trajectory tracking control of characteristic model for nonplanar hex-rotor UAV①

PENG Cheng(彭 程),QIAO Guanyu,CAI Lihua

(Changchun Institute of Optics,Fine Mechanics and Physics,Chinese Academy of Sciences,Changchun 130033,P.R.China)

Abstract

Key words:nonplanar hex-rotor unmanned aerial vehicle(UAV),characteristic model,golden section adaptive controller,stability analysis,trajectory tracking control

0 Introduction

Recently,multi-rotor unmanned aerial vehicle(UAV)has been more and more widely used in military and civil fields due to its advantages of small size,light weight,vertical take-off and landing,strong mobility,free hovering,and even flexible shuttle in narrow and complex environment[1-2].Since multi-rotor UAV is a multi-input multi-output,strong coupling,high-order nonlinear system[3],its flight control technology has become a key issue affecting its practical engineering application.Accurate trajectory tracking is the basic requirement of autonomous flight and has been widely concerned.

For the trajectory tracking control problem of multi-rotor UAV,researchers have carried a lot of researches on quad-rotor UAV as a typical representative.Rios et al.[4]used continuous sliding mode control algorithm to achieve robust tracking of position and attitude for quadrotor UAV with uncertain parameters and external disturbance.Mofid et al.[5]proposed an adaptive super-twisting terminal sliding mode trajectory tracking control algorithm for a quadrotor with input delay.Zakaria et al.[6]designed an H∞robust tracking control method against wind disturbance for quadrotor UAV based on adaptive neural network.Adaptive disturbance compensation trajectory tracking control strategy for quadrotor UAV was proposed and the generalized regression neural network was designed to estimate unknown external disturbances[7].Wang et al.[8]introduced a deep learning method to realize trajectory tracking control of quadrotor UAV.

Thus,for the trajectory tracking control of multirotor UAV,the multi-rotor model is usually greatly simplified to achieve low-order controller design,or a complex nonlinear trajectory tracking controller is designed to control the high-order model.However,complex trajectory tracking methods are difficult to be applied in practical engineering.

In the 1980s,the characteristic model theory was proposed from the perspective of practical application[9].It is a model established by the combination of the dynamic characteristics,environmental characteristics and control performance requirements of the object[10],and its form is simpler than the original dynamic model,easy to design the controller and implement in actual engineering.The characteristic model theory has achieved fruitful results after years of development.Tao et al.[11]designed an adaptive control algorithm based on characteristic model to solve the problem of path tracking control of surface unmanned vehicle under variable environment and time-varying speed.The characteristic model theory and the full coefficient adaptive control method were applied to the joint control of foot robot.The simulation results showed that the method had good control effect and adaptive ability to the model parameter uncertainty in Ref.[12].Considering the attitude control problem of three-axis stable geosynchronous orbit satellites,an improved golden section control method based on characteristic model was adopted.Numerical simulation proved that this method improved the system control performance without increasing energy consumption[13].The characteristic model theory has also been well applied in satellite transient heat flow control,hydraulic kettle control,electrolytic aluminum control and spacecraft return and re-entry control.

Therefore,a trajectory tracking control method based on characteristic model theory for nonplanarhexrotor UAV(simplified as hex-rotor)is proposed.The hex-rotor has a different rotor configuration from the traditional quadrotor UAV,which fundamentally overcomes the problem of the under-actuation of the quadrotor restricting the flight maneuverability,and can realize any configuration of the 6-degree-of-freedom(DOF)motion in space.The characteristic model of the hex-rotor is constructed,the high-order terms and uncertain terms of the hex-rotor are compressed into time-varying characteristic parameters,and the model information is not lost.Moreover,the description form of characteristic model is simple,which is easy to controller design and engineering implementation.Based on the characteristic model of the hex-rotor,a golden section adaptive controller is designed to control the trajectory tracking.Then,the stability of the closedloop system is analyzed and demonstrated in detail.Finally,the trajectory tracking numerical simulation experiments and prototype experiments of the hex-rotor effectively corroborate that the proposed control method in this paper has accurate trajectory tracking control performance and strong robustness against disturbances,which has good practical application value.

1 Dynamic model of hex-rotor

The structure of the hex-rotor is depicted in Fig.1.The plane of the body is composed of six light and equal length connecting rods in the same plane evenly distributed around the center point of the hexrotor.Six drive units(motor and rotor)are mounted vertically at the end of each connecting rod.Among them,rotor 1,3 and 5 rotate counterclockwise,while rotor 2,4 and 6 rotate clockwise.The angle between body plane and rotating shaft isvj(0＜vj＜90°).Two mutually centrosymmetric rotors(rotor 1 and rotor 4,rotor 2 and rotor 5,and rotor 3 and rotor 6)are in the same plane,and the rotation axes of the two adjacent rotors are opposite.The hex-rotor completes horizontal motion and attitude rotation by changing rotor speed,the nonplanar design structure ensures that the hex-rotor can achieve any configuration of the 6-DOF movement in space within the driving capacity of rotors.

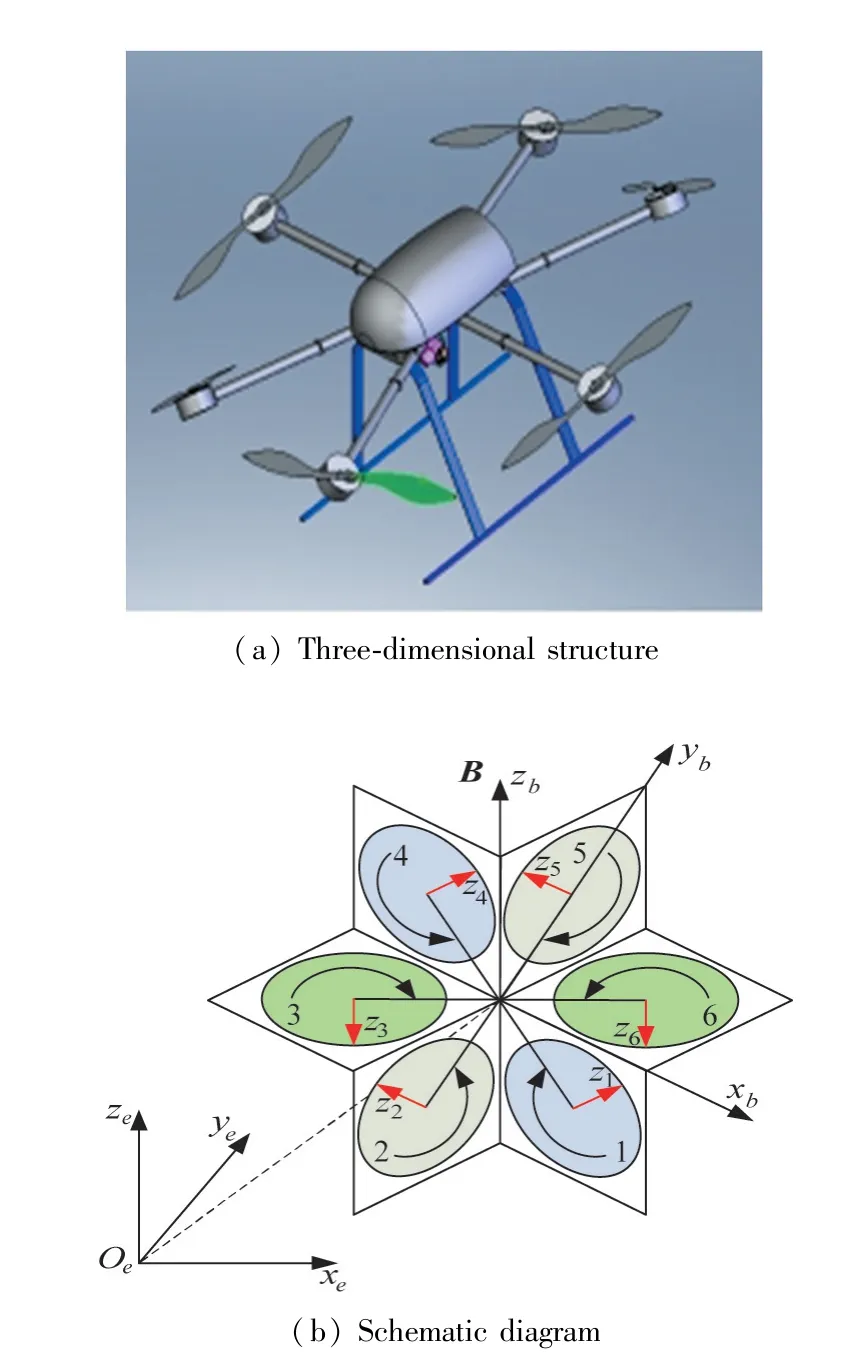
Fig.1 The structure of the hex-rotor

The earth-fixed inertial frameEand the bodyfixed frameBare defined to describe the dynamics of the hex-rotor.The translational space position of the hex-rotor is expressed asP=[Px,Py,Pz]Tand the attitude is defined by Euler anglesη=[φ,θ,ψ]T.The hex-rotor can be regarded as a symmetrical rigid body with 6-DOF in space in the case that the elastic deformation of the rotor is ignored and the aerodynamic characteristics of the rotor are simplified,thus,the rotational dynamic equation is established based on Newton-Euler formula

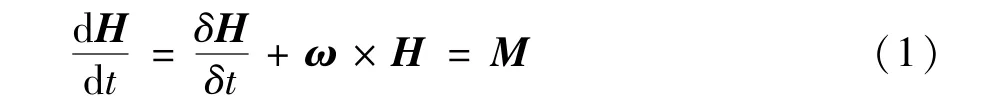
whereω=[p,q,r]Tdenotes the rotational angular velocity in body-fixed frame,the angular momentumH=J·ωwithJ=diag(Ix,Iy,Iz)andIx,Iy,Izare moment of inertia in three axis.The resultant moment of body-fixed frameMis expressed as

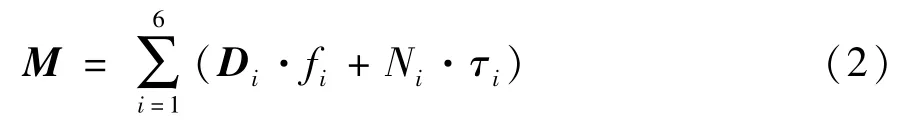
whereDi∈R3andNi∈R3,i=1,2,…,6 respectively represent the position vector and direction vector of the rotor in the body-fixed frame,which can be obtained as

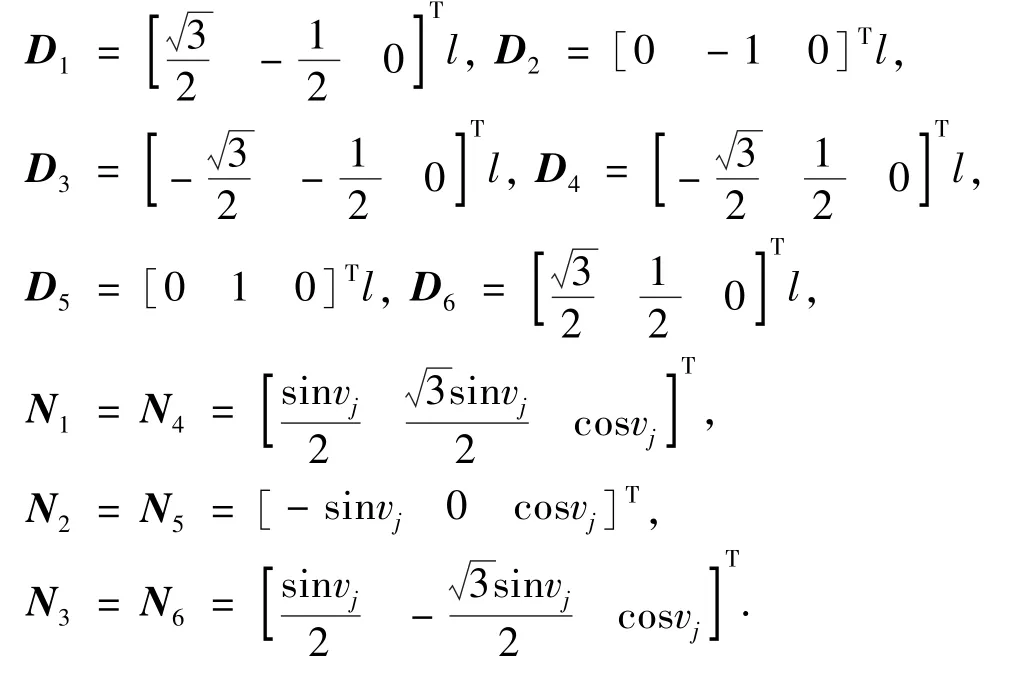
wherelrepresents the distance between the rotor and the center of the hex-rotor,fi=k1Ω2idenotes thrust generated by theith rotor,as well asτi=(-1)i-1k2Ω2iexpresses the reactive torque,withΩias the speed of theith rotor.k1andk2are the thrust factor and drag factor.

The relationship between Euler rates and the body angular velocity is described aṡη=T·ωwith transfer matrixTas

Then,the rotational dynamic equation can be derived as

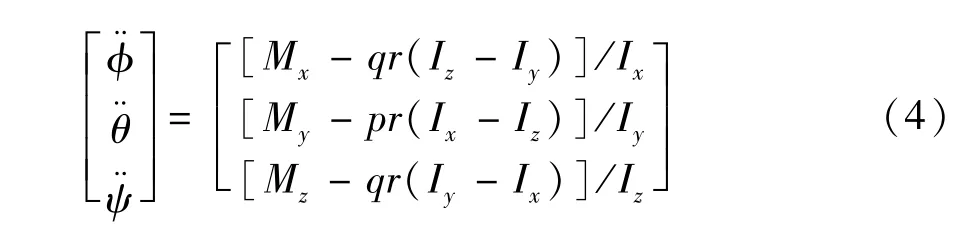
whereMx,MyandMzare the axial component of bodyfixed frame.

The translational dynamics equation of the hex-rotor inearth-fixed inertial frame is established as

whereRis called the rotation matrix maps vectors from the body-fixed frame to the inertial frame[14].G=[0 0g]Twithgas the acceleration of gravity,the resultant forceF=[Fx Fy Fz]Tis written by

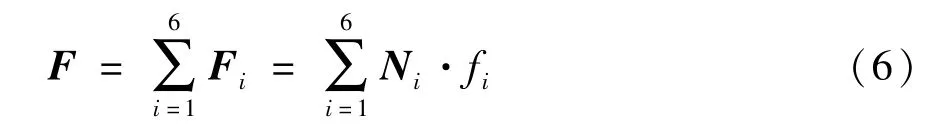
Substituting Eq.(6)into Eq.(5),then,the translational dynamics equation can be given by

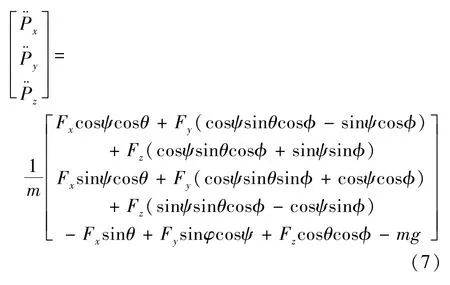
2 Characteristic modelling of hex-rotor

It can be noted from the dynamic model that the hex-rotor is a multi-input multi-output nonlinear complex system with strong coupling.It is often difficult to design a low order controller that is easy to implement in engineering to achieve high performance control for such complex nonlinear system.Therefore,the trajectory tracking control method based on characteristic model for the hex-rotor is proposed in this paper to solve the problem in the design of low level controller under accurate modeling to meet high performance control requirements,so as to improve the track tracking control performance of the hex-rotor.The difference equation between the control input and system output variables can be established based on characteristic model theory to facilitate the design of the controller[15-16].The characteristic model is not a reduction of the high order model,but concentrates the relevant information of the system model into the characteristic parameters without losing information.It is equivalent to the output of the real object under the same input control,and has much simpler form,which is easy to design the subsequent controller and facilitate the realization in actual engineering.

In the general case of small attitude angles of the hex-rotor,the translational error dynamics equation is rewritten as

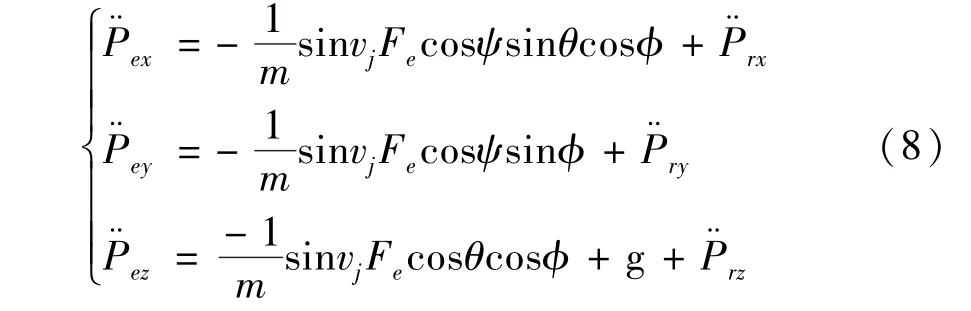
wherePr=[Prx,Pry,Prz]Texpresses the desired translational position of the hex-rotor,andPe=[Pex,Pey,Pez]Tis the translational position error,namely,it is the difference between the desired translational position and the actual translational position.Taking the fourth derivative of Eq.(8)can be obtained

whereAjexpresses theith row vector of matrixA,Bs(x)=(bs,ij(x))3×4(s=0,1,2;i=1,2,3),and then addinġxjto both sides of Eq.(10)the following can be obtained as

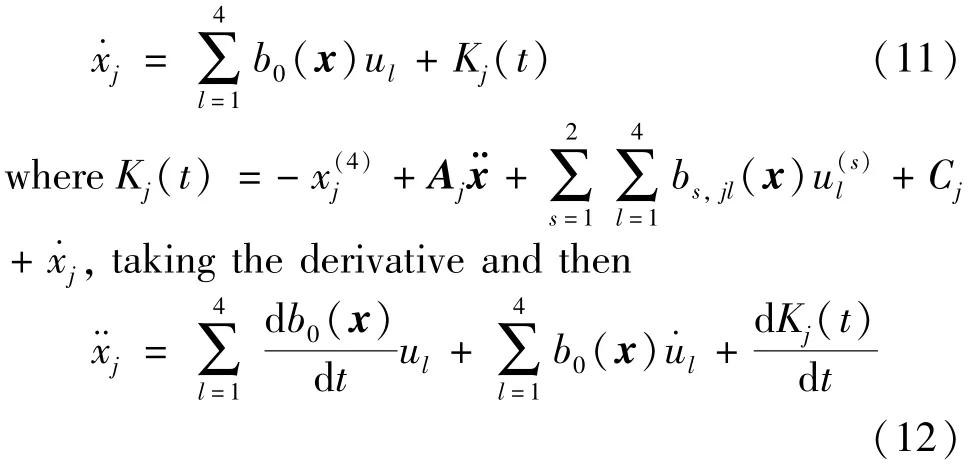
Eq.(13)can be obtained by adding Eq.(11)and Eq.(12)after discretization.

wherefj1(k)=2-T,fj2(k)=T-1,Tdenotes system sampling period,gjl(k)=T2b0(x(k))+2Tb0(x(k))-Tb0(x(k-1)),gj,p+l(k)=-Tb0(x(k)),Wj(k)=(T2+T)K(k)-TK(k-1),fj1(k)andfj2(k)can be determined directly whenTis fixed.The elements ofAjare bounded due to the bounded derivatives ofulandxj.|Wj(k)|≤2MjT+MjT2whereMjis positive coefficient.Then,|Wj(k)|=0,That is,whenTis sufficiently small,the modeling error can be less than the given error limit.As a result,the characteristic model of the hex-rotor can be expressed as

wherex(k+1)represents the discrete vector of the output trajectory error at timek+1,similarly,x(k)andx(k-1)denote the discrete vector of the output trajectory error at timekandk-1,respectively.u(k)andu(k-1)are the discrete vector of the controlling quantity at timekandk-1;F1(k),F2(k),G0(k)andG1(k)express characteristic parameters with slow time-varying.

3 Trajectory tracking adaptive controller design

In the system startup stage,for the controlled object with unknown parameters,the general adaptive control algorithm is difficult to ensure the stability of the system,which results in running by mistake.Thereby,the golden section ratio combined with minimum variance is introduced in this paper,the golden section adaptive controller is designed as follows based on characteristic model of the hex-rotor for the sake of stability in transition.

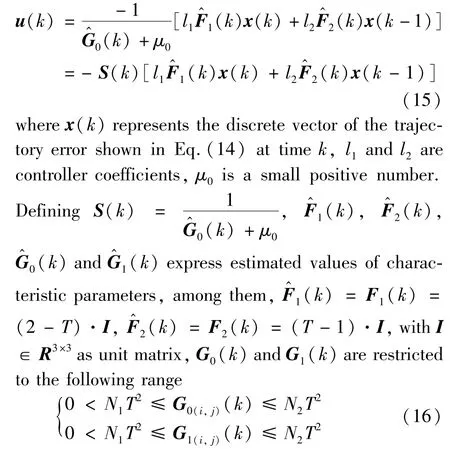
withi=1,2,3;j=1,2,3,4;N1andN2are positive numbers;G0(k)andG1(k)are estimated based on recursive least square method with forgetting factor devised as

4 Closed loop stability analysis

The stability of closed loophex-rotor system is analyzed and the following proposition is described.

Proposition 1Taking consideration of characteristic model of the hex-rotor shown in Eq.(14)and golden section adaptive controller expressed in Eq.(15),if the following two conditions are met:

ProofSubstituting Eq.(15)into Eq.(14),it can be derived that

Utilizing Gronwall-Bellman inequality,it can be obtained as

Therefore,it is obviously noted that the closed loop hex-rotor system with adaptive controller based on characteristic model is exponentially stable.

5 Numerical simulation results

From the point of view of practical application,firstly,the trajectory tracking control simulations of the hex-rotor between the proposed method and proportional integral derivative(PID)method widely used in engineering are carried out to demonstrate the validity and robustness of the proposed method in two cases.The parameters of model in simulations are taken from the hex-rotor prototype,as listed in Table 1.The adaptive controller coefficients are taken asl1=0.382,l2=0.618,andμ0=0.01.The sampling period is set asT=0.01s,andN1=1,N2=100,forgetting factor is chosen asλ=0.996,ξ(0)is randomly selected in the following range

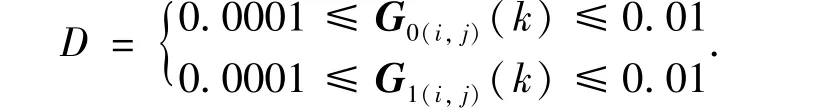
Table 1 Parameters of the hex-rotor prototype

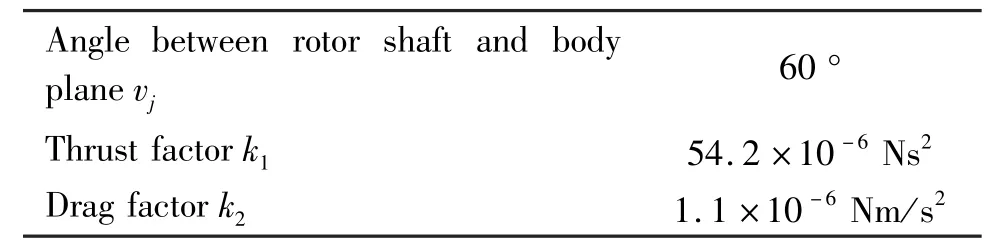
Angle between rotor shaft and body plane vj 60 °Thrust factor k1 54.2×10-6 Ns2 Drag factor k2 1.1×10-6 Nm/s2

In the first case,assume the initial trajectory positon asP0=[0 0 0]Tm,and the desired trajectory is inclined space rectangle depicted as

Fig.2 and Fig.3 describe the rectangular trajectory tracking three dimensional curves based on the proposed method and PID algorithm,respectively,in which it can be noted that the hex-rotor system has more accurate trajectory tracking control performance with the proposed method.To further clarify the comparison results of two algorithms,the rectangular trajectory in positionx,yandzdirections with two algorithms are depicted in Fig.4.It is clear to see that the adaptive controller based on characteristic model has much smaller overshoot,faster response time and more satisfied trajectory tracking effect with zero stable error in three directions.

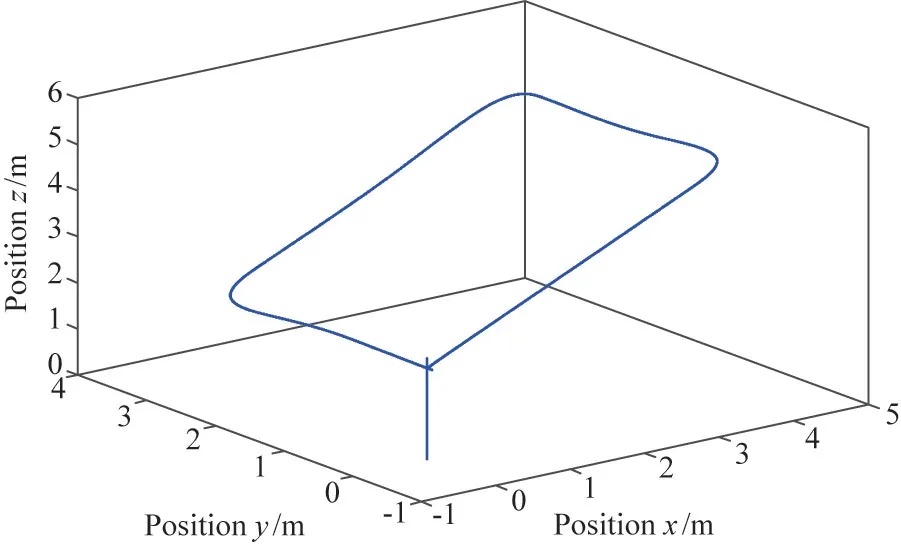
Fig.2 Rectangular trajectory tracking three dimensional curves with the proposed method

Fig.3 Rectangular trajectory tracking three dimensional curves with PID method

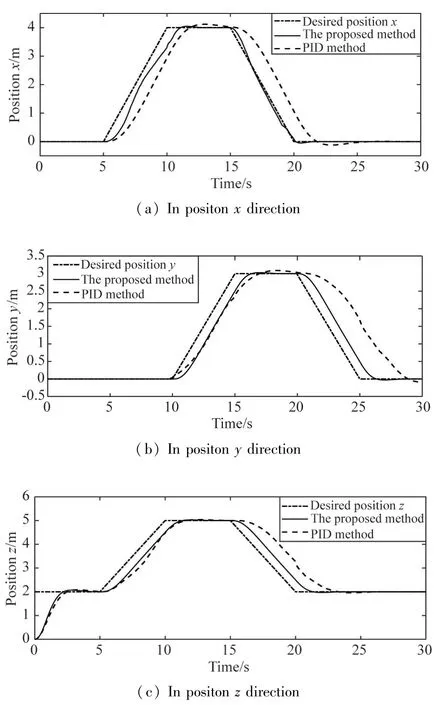
Fig.4 Rectangular trajectory tracking simulation results in three directions

Additionally,the estimations of characteristic parameters based on recursive least square method with forgetting factor are shown in Fig.5 and Fig.6.It can be remarkably obtained that the estimated values ofG0(k)andG1(k)eventually tend to the constant value with fast convergence rate.

Fig.5 Estimation results of characteristic parameter G0(k)

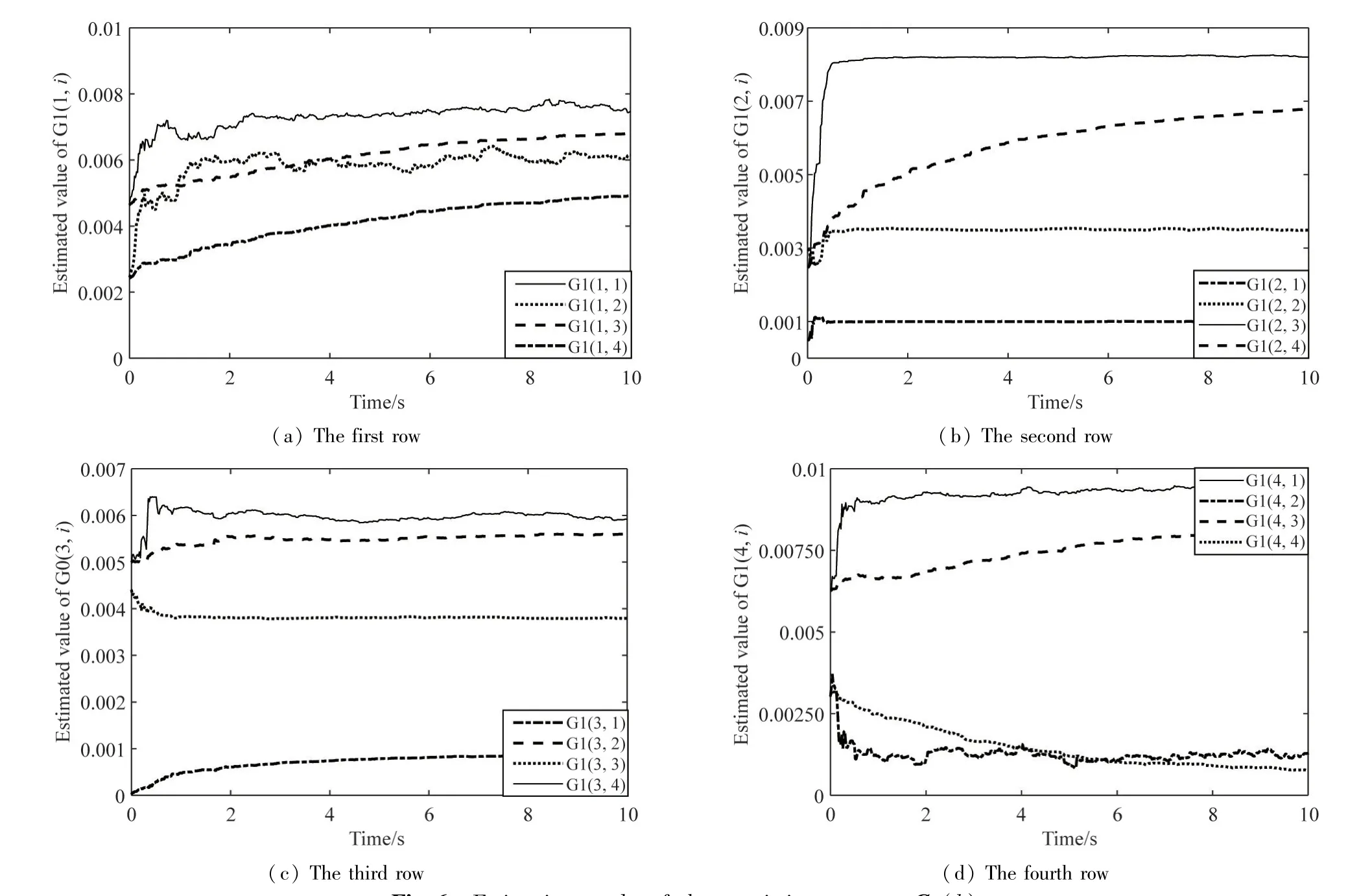
Fig.6 Estimation results of characteristic parameter G1(k)

Further,the second simulation is implemented for sake of verifying the robustness of the proposed method.The white noise with the amplitude of 0.15 Nm as external disturbance is acted on the three position directions.The initial trajectory positon is also assumed asP0=[0 0 0]Tm,and the desired trajectory is space ellipse described as

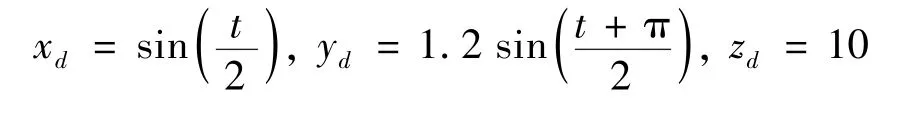
The ellipse trajectory tracking results based on the proposed method and PID are shown in Fig.7 and Fig.8.The proposed controller has significantly smaller overshoot and much stronger robustness against external disturbance than PID method.The trajectory errors in three directions of the two strategies are exhibited in Fig.9,in the meanwhile,the maximum absolute error(MAX)and root mean square(RMS)error in three directions from 4-50 s are provided quantitatively in Table 2.The results illustrate that the ellipse trajectory tracking stable errors in three directions of the proposed method are maintained in the smaller magnitude with a faster response speed under external disturbance.

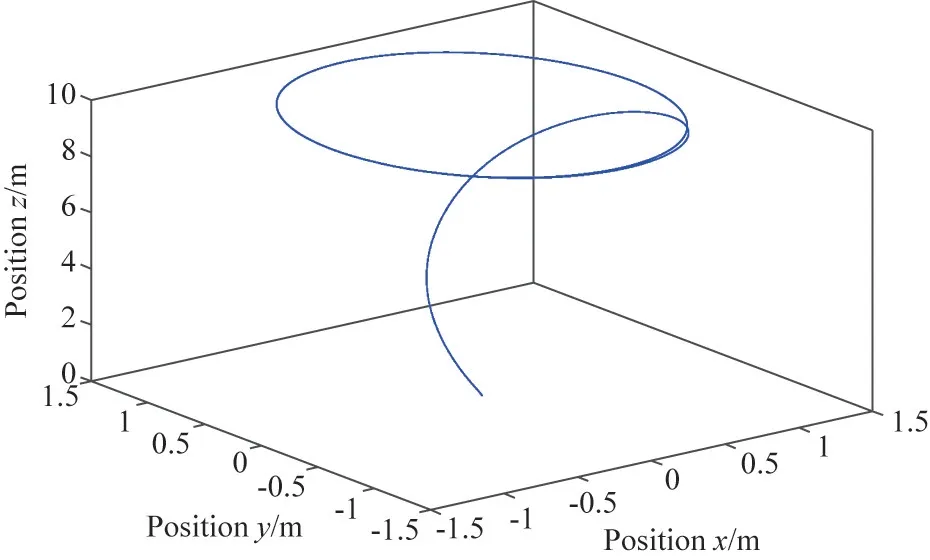
Fig.7 Ellipse trajectory tracking three dimensional curves with the proposed method

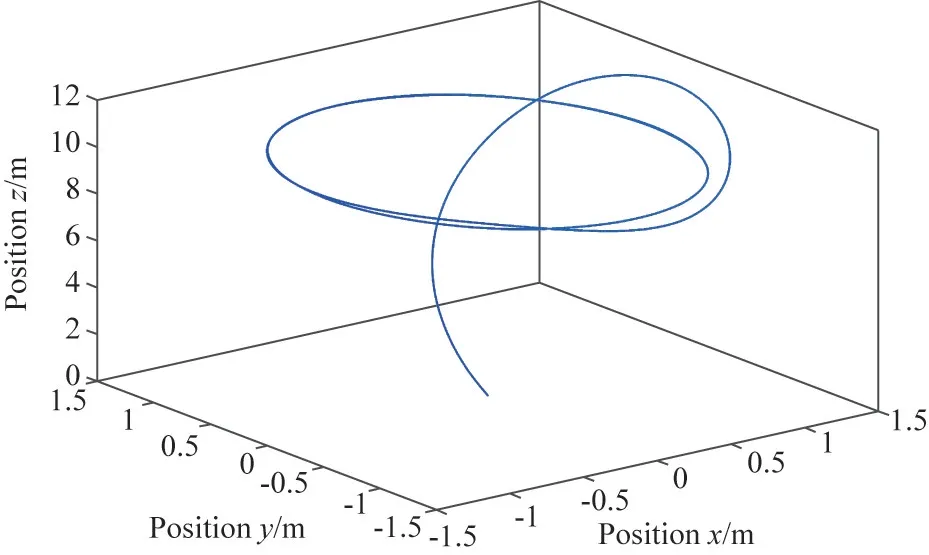
Fig.8 Ellipse trajectory tracking three dimensional curves with PID method

Fig.9 Ellipse trajectory tracking errors in three directions

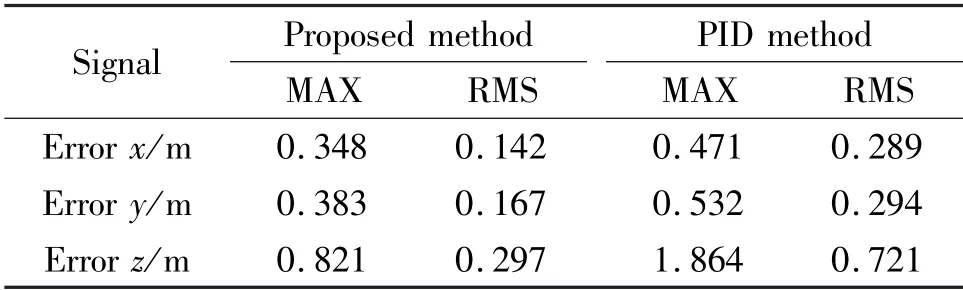
Table 2 Ellipse trajectory tracking compared errors of MAX and RMS

6 Hex-rotor prototype experiments

The schematic view of hex-rotor control platform is presented in Fig.10.It uses DSP with the series of TMS320F28335 that runs at 150 MHz,including 12 programmable pulse width modulation outputs,12-bit analog input as well as 16 channels with programmable gains,at the same time,it supports floating point calculations as the hex-rotor on-board control computer.

Fig.10 The schematic view of hex-rotor control platform

Distance laser sensor and inertial measurement unit(IMU)constituted by accelerometers,magnetometers and gyroscopes are installed on the hex-rotor prototype to measure flight states.The RS232 serial port can transmit the sensor data to the on-board control computer.Then,the host computer receives these data exported from on-board computer through wireless transfer and generates the corresponding analysis charts,which provides prototype experimental support.

For the sake of demonstrating feasibility and robustness of the proposed adaptive controller in the actual engineering,the fixed point anti-disturbance experiment and triangle trajectory tracking experiment of the hex-rotor prototype outdoors are carried out.The parameters of the adaptive controller and estimation values of characteristic parameters are the same as those in simulations.The hex-rotor experimental flight picture is displayed in Fig.11.

Fig.11 The hex-rotor prototype

Firstly,the instantaneous maximum wind speed is about 4.5 m/s measured by the tachometer in the fixed point anti-disturbance experiment outdoors.The fixed point trajectory tracking results in three directions are shown in Fig.12.It is worthwhile to point out that although the track errors in the three directions are large due to wind disturbance,the hex-rotor quickly overcomes the influence of external disturbance based on the proposed method in this paper,and the stable errors of three directions all converge within±1 m.The results highlight the claim that the adaptive controller with characteristic model has favorable trajectory tracking control performance and strong robustness in the presence of wind disturbances.

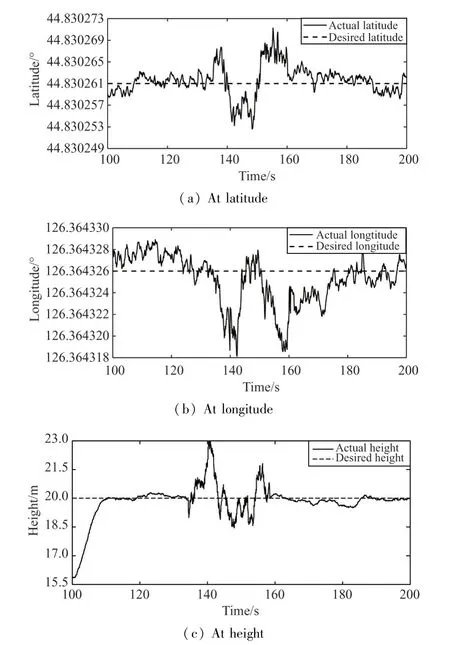
Fig.12 Fixed point trajectory tracking results in three directions of hex-rotor prototype

Further,the triangle trajectory tracking prototype experiment is executed with three-level varied wind disturbance outdoors.Fig.13 clearly indicates that the proposed method can reach the desired trajectory and offer the great tracking control performance.It is obtained that the adaptive controller with characteristic model is well suited in dealing with the trajectory tracking control problem in actual engineering.

Fig.13 Triangle trajectory tracking results in three directions of hex-rotor prototype

7 Conclusion

Aiming at the high performance trajectory tracking controller design problem for strongly coupled nonlinear hex-rotor UAV with high driving property,great payload capacity and damage tolerance in practical engineering,an adaptive trajectory tracking controller based on characteristic model is proposed in this paper.Firstly,the dynamic model and characteristic model of the nonplanar hex-rotor is constructed.On the basis of characteristic model,a golden section adaptive controller is designed.Then,the stability of the hexrotor closed loop system is analyzed in detail.Finally,numerical simulations in two cases demonstrate the effectiveness of the proposed method under disturbances.In the meanwhile,two kinds of prototype experiments indicate the hex-rotor system based on the proposed method can provide the favorable trajectory tracking control performance with stable error converging to±1 m as well as strong robustness in the presence of three-level wind disturbances outdoors.