对一类圆锥曲线定值问题的探究
2022-02-11江苏省南通市海门证大中学226100周雅俊
江苏省南通市海门证大中学 (226100) 周雅俊
平面解析几何在《普通高中数学课程标准(2017年版2020年修订)》中放入几何与代数主题中,核心思想是以代数的方法解决几何问题,重点提升学生的直观想象、数学运算、数学建模、逻辑推理和数学抽象的数学核心素养.教师在教学时要引导学生多角度地研究问题、多层次地探究问题,达到做一道会一类,促进学生的数学核心素养的提升.笔者在与学生一起解题时,和学生一起发现了一类圆锥曲线的定值问题的一些性质,整理成文.本文仅以焦点在x轴上的圆锥曲线加以说明,仅作抛砖引玉,期待得到大家的指点.
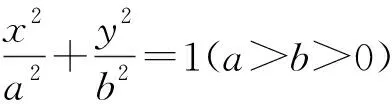
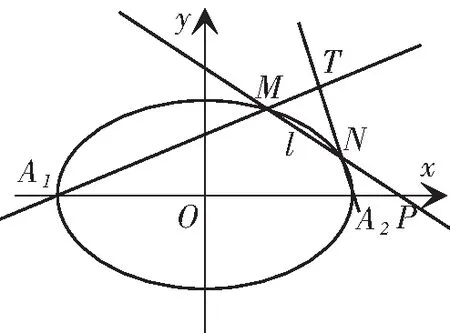
图1

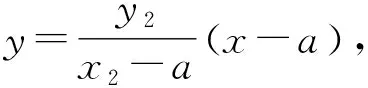
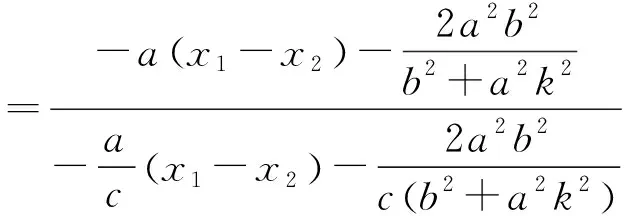
性质1中是过右准线与x轴的交点作一条直线,得出交点T的横坐标为定值.类似的可以过椭圆的右焦点作一条直线,于是得到如下性质.
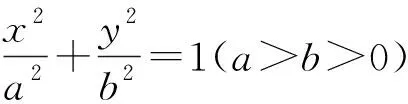
同为有心二次曲线,双曲线也具有相似的性质,进一步探究发现了以下的性质.
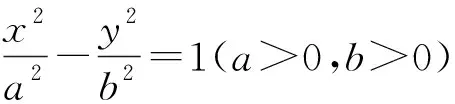
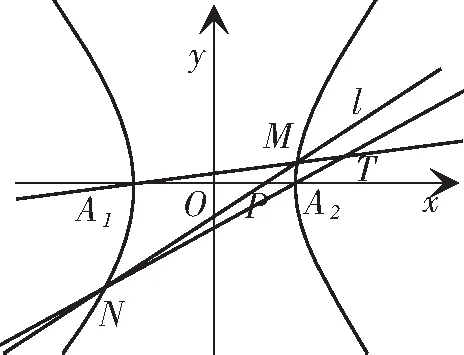
图2
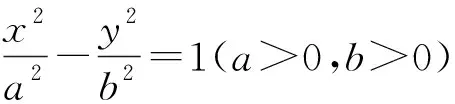
性质2、3、4的证明类似于性质1,这里就不赘述了,有兴趣的读者可以自己尝试去证明.这样的话可以归纳出有心圆锥曲线的两个共同的性质,这里仅以焦点在x轴上有心圆锥曲线作说明.
共同性质1 在一个有心圆锥曲线中,左右顶点分别是A1、A2,右准线与x轴的交点是P,过点P的直线l与这个圆锥曲线交于M、N两点,过右焦点作x轴的垂线m,设直线A1M、A2N相交于点T,则点T在定直线m上.
共同性质2 在一个有心圆锥曲线中,左、右顶点分别是A1、A2,过右焦点F的直线l与这个圆锥曲线交于M、N两点,设直线A1M、A2N相交于点T,则点T在右准线上.
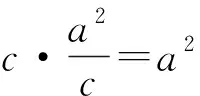
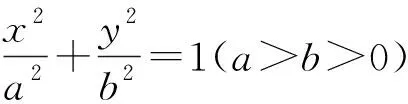
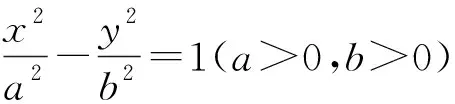
从广义上来说,圆也是圆锥曲线,当平面只与圆锥面一侧相交,且不过圆锥顶点,并与圆锥的对称轴垂直,结果为圆 ,这样也可以得到一个推广.
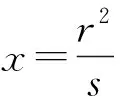
与有心二次曲线有所不同,抛物线与对称轴只有一个交点,由射影几何的知识知道:一个平面内两条直线平行,那么这两条直线就交于这两条直线共有的无穷远点.这样的话可以大胆地猜想抛物线与对称轴的另一个交点在抛物线对称轴上的无穷远处,经过小心地求证,于是就有了以下的性质.
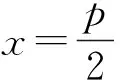
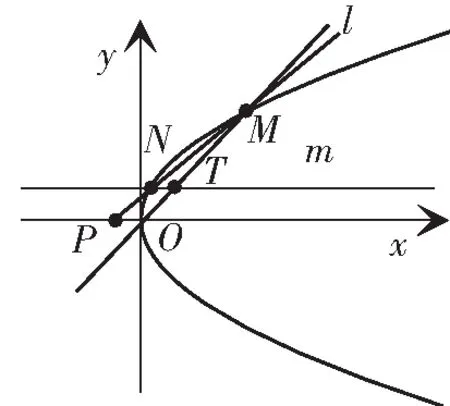
图3
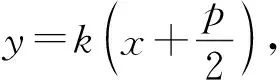
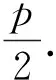
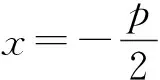
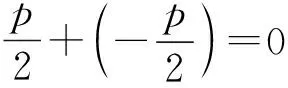
推广4 在抛物线y2=2px(p>0)中,过x轴上一点S(s,0),作直线l与抛物线交于M、N两点,过点N作x轴的平行线m,直线OM与直线m相交于点T,则点T在定直线x=-s上.
在性质1中,当M、N两点无限接近至重合时,这时M、N、T三点重合,直线l也就变成了椭圆的切线.性质3、5也可以进行类似的演绎,得到相似的结论.这样可以得到圆锥曲线的一个公共性质,这里仅以焦点在x轴上的加以说明:在一个圆锥曲线中,焦点是F,其对应的准线与x轴的交点是P,过点F作x轴的垂线l,与这个圆锥曲线交于M、N两点,则直线PM、PN与这个圆锥曲线相切.类似上面的三个推广,这个性质也可以加推广.
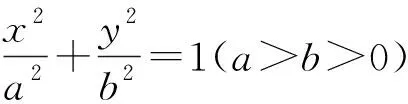
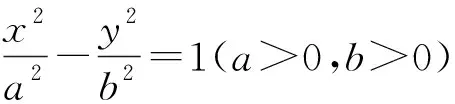
推广7 在抛物线y2=2px(p>0)中,x轴上有两点S(s,0),T(t,0)(t>0),s+t=0,过点T作x轴的垂线l,与抛物线交于M、N两点,则直线SM、SN抛物线相切.
一道好的试题研究价值不应仅仅停留在解法上,还应该对试题本身做深入的探究,挖掘深层次的数学内涵,通过变式教学、引导学生探究、揭示数学本质[1].试题要发挥其最大功效,要进行拓展研究,挖掘试题的原理.马波教授在《中学数学解题研究》中说到:开展解题研究,选择适当的问题,从解题的某一个侧面加以总结、概括、提升.教师在试题讲解时应该注意创设合适的教学情境,启发学生思考,大胆地假设、小心地求证,引导学生把握数学的本质.
