一道向量题的多角度探析
2022-02-11江苏省如皋中学745099
江苏省如皋中学 (745099) 王 涛
在教学过程中,对于一些典型问题,尤其是高考真题,如果我们能够从不同角度思考,寻求不同的解法,以一题多解的方式寻求知识间的内在联系,构建知识的网络体系,加深对问题的本质认识,定会拓宽解题视野,发散解题思维,提升学习兴趣,提高解题能力.本文是笔者对一道向量难题的研究,现与读者分享交流.
1 试题呈现与分析

分析:该题形式上考查向量模和的最大值,考虑向量具有代数与几何的双重属性,我们将问题转化为函数问题处理,主要考查分析、解决向量问题的能力,强化对转化与化归、数形结合、消元与不等式求最值等数学思想方法的考查,体现了逻辑推理、数学运算等数学核心素养.试题结构虽简单、明了,但内涵丰富,本文尝试对该题从不同的角度予以思考,给出不同的解法.
2 解法探究

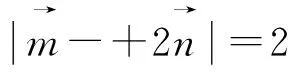
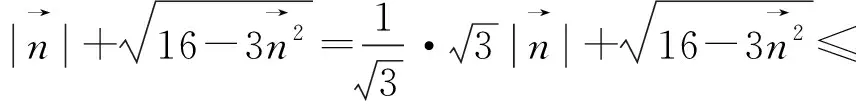


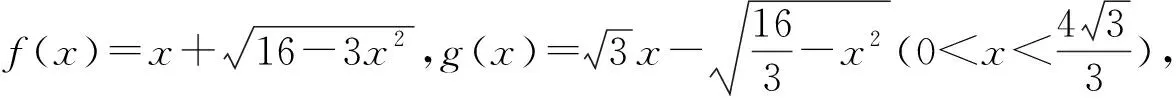
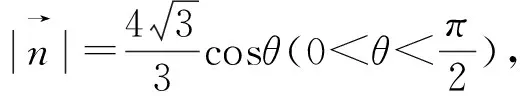
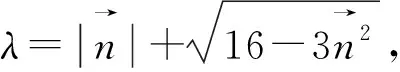
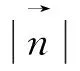

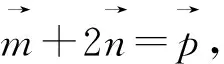
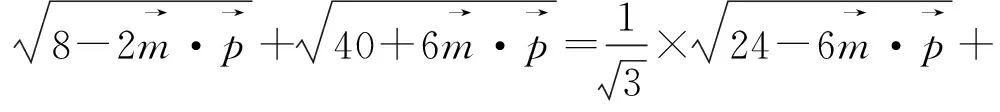
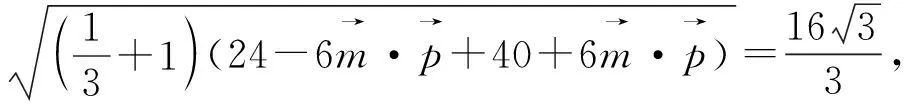
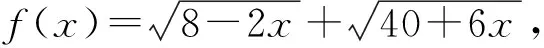
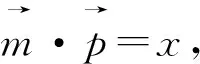
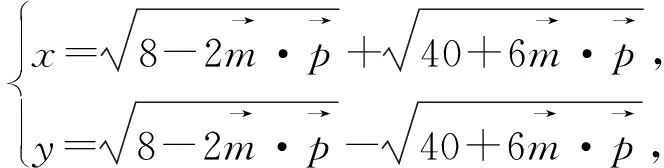


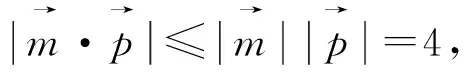

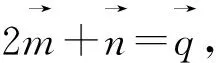



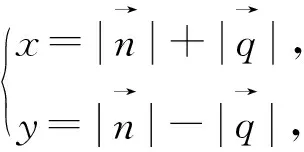


图1
评注:除了对条件式换元,还可以从目标式入手,对目标式采用换元法,将问题转化为二元二次方程(3x2+y2=16 (x,y>0))条件下的二元函数(x+y)最值问题 ,这里提供5种方法供读者学习.
角度4:借助坐标,将问题转化为二元二次方程( 圆方程)条件下的二元函数最值问题 .
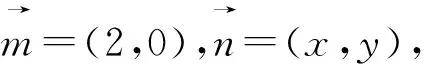
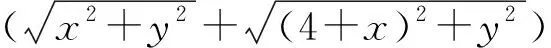
3 反思总结
从不同的角度出发思考问题,得到以上不同解法,思维方式的不同带来解答形式的不同,给考生极大的思考与解答空间,在运算量和解答时间上出现差别,区分出不同层次的考生,具有很好的信度与区分度.一题多解不仅增加了问题涉及的知识广度,而且以一带多,可以减少考查同样多知识的题量.在日常解题教学中,教师要善于通过解题发现知识间的内在联系,体会知识间的转化与化归,构建知识间的网络体系.这样,学生在学习基础知识,掌握基本技能的同时,可以有效锻炼思维的深刻性、广阔性、灵活性和创新性,达到举一反三、融会贯通的解题水平和能力,但在日常的学习中,要结合自身掌握程度和实际情况,选择最佳方法,不要一味追求某一种解法或过分追求一题多解,而是学会从不同解法中汲取不同的数学思想,从而提高自身的数学核心素养.
