未知空间目标纹理缺失表面三维重建算法

黄烨飞，张泽旭，崔祜涛

(哈尔滨工业大学航天学院深空探测基础研究中心，哈尔滨 150080)

0 引 言

获取空间目标的高精度形貌与完整三维结构是在轨服务与维护的基础。相较于利用激光扫描获取空间目标结构，基于多视图几何原理重建目标三维结构的技术，即从运动恢复结构(Structure from motion，SfM)技术，在工作频率和重建精度上均有较大提升，也是现在计算机视觉在航天领域的重要应用之一。

传统的多视图几何技术需要从像素梯度信息中提取特征点，并在不同图像间构建特征点的对应关系。对于纹理丰富的区域，传统算法能够提取大量稳定的特征位置，进而在恢复目标结构时产生较为稠密的结果。

然而，对于光滑且缺乏纹理的目标区域，如卫星表面因反射导致的高亮度区域，缺失的特征点导致重建结果的缺失。另一方面，对于空间目标中的相似特征点，如太阳能电池的角点等，传统的SfM过程并不能获取特征点在图像中相对其他特征的全局位置信息，错误的匹配关系也可能导致重建结果的不完整。文献[1]通过对核线图进行边缘检测以解决图像弱纹理区域匹配问题，文献[2]融合倾斜摄影和激光扫描提高重建结果的完整性。然而这些方法其本质上依然沿用增强图像纹理特征、利用相机组限制图像匹配范围[3]的思路，并不能解决传统算法对于特征独特性的依赖。

近年来随着深度学习技术的发展，基于深度学习的三维重建技术在提高重建精度、完整性以及运算速度等方面有着巨大的潜力。利用基于训练获得的特征提取和匹配过程代替传统人为设计的图像特征提取和描述，可以将图像的全局信息引入局部的特征描述中，从而提升特征提取的数量以及匹配结果，进而缓解纹理缺失区域的重建结果完整性问题。如文献[4]利用深度学习模块替代了传统特征提取的响应计算、主方向计算和描述过程，文献[5]在构建特征描述过程中进行了额外的全局信息整合，文献[6]利用大量仿真角点图像进行预训练等。但是这类算法仅提升了特征点提取和匹配的性能，并不能完全解决重建的完整性问题。

除了上述利用深度学习对传统重建技术进行改进的策略，另一种策略通过输入图像序列以及对应的相机外参，将整个重建空间进行立体网格划分，并直接对重建空间进行估计以获得目标的三维结构[7-8]。这类端到端的深度学习框架通过对三维空间进行插值构建目标表面，极大提升了三维重建结果的完整性。然而，其重建精度受限于网格大小划分，同时，其输出结果极大占用内存空间造成模型训练困难。

近年来，基于逐像素深度估计的三维重建算法有效地缓解了内存空间的消耗问题。通过输入序列图像以及对应的相机外参，利用深度学习框架获取序列图像初始参考帧中任意像素的深度，并最终整合多个图像序列获得目标的完整三维结构。文献[9-10]中，通过多个卷积层提取图像特征，并提出对不同深度平面通过单应性变化构建三维的视差损失张量(Cost Volume)以表征图像间相同像素位置的对应情况。然而，此类方法在卷积过程中仅保留原始图像1/16尺寸，丢失了部分深度信息。研究过程中进一步发现，此类算法对于航天场景中的空间目标仿真图像并不适用。

为了实现未知空间目标纹理缺失表面的完整三维重建，本文设计了一种通过神经网络估计像素深度，并利用截断符号距离函数(Truncated signed distance function, TSDF)进行表面重建的算法。本文设计的神经网络框架借鉴了MVSNet[9]中利用深度区间计算Cost Volume的设计策略，通过计算不同深度间隔在图像间的投影关系计算Cost Volume，保证了网络对不同长度图像序列的稳定性。但是本文所设计网络结构舍弃了单独的特征提取模块，同时在获得1/16深度图后，通过上采样以及重投影过程，实现在原始图像尺寸下的像素深度估计。在获取单幅图像深度图后，将深度估计网络对特征点的估计误差作为图像筛选的阈值，并利用TSDF对不同序列的深度估计结果进行融合，恢复目标表面结构。仿真校验结果表明，本文所设计算法在保证重建精度的同时，极大提高了重建结果的完整性。

1 深度估计网络结构设计

1.1 图像Cost Volume计算

参考图像I中的任意像素P=(u,v, 1)T，将其对应的3×3相机内参矩阵记作K，则该像素转换到相机归一化坐标系下为K-1P。假设其深度为z，则该像素对应在参考坐标系下的空间点为z·K-1P。

若图像I′与参考图像相对运动为R,t，可将该空间点投影至该幅图像对应的相机坐标系下，得到其投影点PI′=R·z·K-1P+t。

将PI′=(x1,y1,z1)T归一化为：

(1)

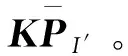
将深度区间(dmin,dmax]等距离散化为n个预估值di：

(2)

式中：i=1,2,…,n表示深度区间编号。

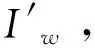
(3)

对于3×H×W的RGB图像，其3个通道均对应n个不同深度估计di下的转换图像I′w，最终构成3n×H×W的三维张量。

假设一个图像序列中有m幅图像，将第一帧图像作为参考帧，后续m-1幅图像通过其对应的相对运动信息可得m-1个三维张量Tj(j=1,2,…,m-1)。

根据式(4)计算此三维张量在该图像序列中的方差C：

(4)

式中：(·)*2表示张量中逐元素求幂运算。

将方差C作为该图像序列的Cost Volume用于后续的深度估计过程。Cost Volume的计算解决了图像序列长度对于深度学习模型的影响，对于任意长度m的序列图像，均可将其转化为3n×H×W的张量，从而保证了深度学习模型对不同图像序列的稳定性。

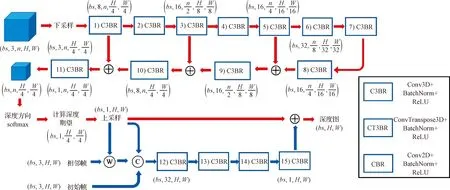
图1 深度估计网络结构Fig.1 Model design for depth estimation

1.2 网络结构设计

通过计算Cost Volume，将任意长度的图像序列转换为固定3n×H×W的张量，进一步将其拆分为3×n×H×W，设计深度网络模型如图1，实现逐像素的深度估计。

图1中bs表示训练过程batch大小，表示将该序列图像中的相邻帧根据式(3)进行图像转换，©表示将多个张量在深度方向上进行叠加。为更加直观地描述维度变化过程，经过每一层处理后的张量维度标注在该层模块的上/下方，未特别标注的各层维度与其前一层保持一致。

在计算图像序列Cost Volume后，将其在图像长和宽方向下采样至原始尺寸1/16，通过三维卷积和逆卷积模块实现对1/16图像中任意位置产生n维向量。在深度方向上通过softmax(·)函数，将n维向量转化为对应预设n个深度区间的概率，计算该向量的期望作为该像素位置的深度估计结果，以保证深度估计过程的连续可导[8]。

在获取1/16图像深度后，首先通过上采样过程将其恢复至原始图像尺寸大小。为了解决上采样过程造成的误差，将深度图与图像序列初始参考帧以及相邻帧进行叠加，利用4个二维卷积层实现对深度图的优化。整体网络结构中，各层kernel size均为3，padding均为1，第8～10层额外设定参数output padding分别为(1，1，1)、(1，0，0)和(1，1，1)，其余对应参数设置如表1。

表1 网络参数设置Table 1 Settings of the CNN model

2 基于深度图的表面重建

2.1 基于TSDF的表面表征

利用截断符号距离函数(Truncated signed distance function, TSDF)进行表面重建原理如文献[11]所述。将三维空间均分为若干体素的集合X，记当前体素x(x∈X),di(x)表示第i次观测下，沿相机光心通过体素x射向物体表面的深度，cz(x)表示体素x在相机坐标系z方向的深度，t表示参与表面重建融合迭代过程的体素深度范围，则通过式(5)可将三维空间中任意体素x赋值为ti(x)，且满足ti(x)∈[-1, 1]。

(5)

ti(x)<0表示该体素位于物体内部，ti(x)>0表示体素位于外部开放空间，ti(x)=0时表明体素x在当前相机观测结果中位于物体表面。

初始化对体素x的观测结果T0(x)=0，以及对应的置信度W0(x)=0，记融合了i(i≥1)次观测后的观测结果为Ti(x)，其对应的体素置信度为Wi(x)。则对体素x的观测融合过程如式(6)：

(6)

以wi(x)表示第i次观测过程对体素x的置信度，相机视野范围内的体素置信度设为1，其余为0。

通过式(6)，将不同观测位置下的观测结果进行融合，得到基于TSDF表征的三维空间Ti(X)，对其进行插值，Ti(X)=0即为在不同位置下观测获得的目标表面结果。

2.2 基于CUDA的重建过程

2.2.1三维重建空间构建

对于内参为fx,fy,cx,cy的标准相机模型，从像素坐标(u,v, 1)T到相机系坐标(x,y,z)T有如式(7)转换关系：

(7)

进一步可得：

(8)

对于任意一幅图像，通过深度图，获取其观测到物体最大深度为dmax，构建如图2所示锥形空间，视锥体顶点为相机光心，四个底角分别为最大深度下图像四个顶点对应的空间位置。

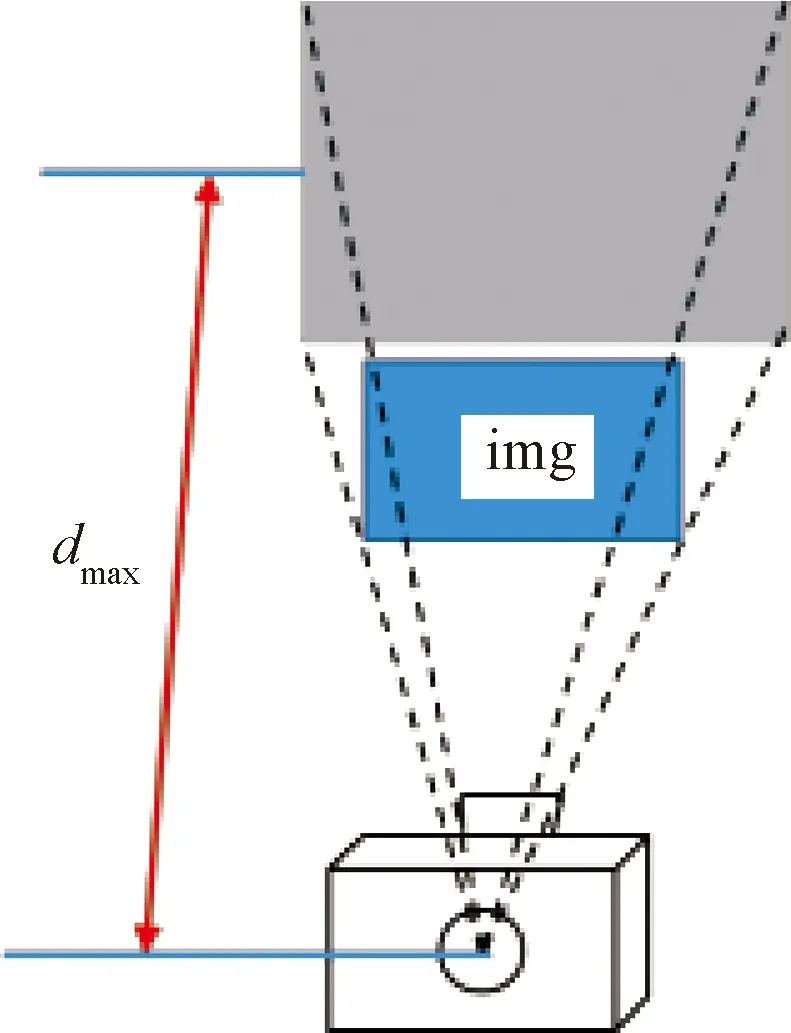
图2 相机视锥体Fig.2 Schematic of the view frustum

对于像素坐标系中图像右下位置(u0,v0, 1)T，根据式(8)得到对应相机坐标系中视锥体右下位置坐标：

(9)

通过类似过程，可以得到视锥体左上、右上、左下位置坐标。根据该相机坐标系相对于参考系姿态信息，可进一步将该视锥体中心以及四个底角位置转换至参考坐标系下，分别计算其在参考系三轴范围内的深度区间，通过不同视锥体在参考系下的值域范围，生成用于目标重建的三维空间。

2.2.2CUDA并行计算分配

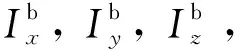
由于GPU中grid由多个block组成，可得block索引为：

(10)

单个block中最大线程数为Mthread, block中的线程索引(thread index)为i。则该线程在单个GPU并行计算的所有线程中索引为：

Ithread=Iblock×Mthread+i

(11)

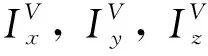
(12)

3 仿真实验校验

3.1 仿真图像生成

仿真图像生成过程中共计使用14个不同模型，其中11个来自微软3D库，用于扩充模型的多样性，其余3个模型分别为北斗卫星、OSIRIS-REx卫星和ICESat-2卫星。所有模型均缩放至约300 mm，为了防止过拟合，实际模型最大边长缩放为270～350 mm。

仿真场景如图3，目标尺寸约为300 mm，且相邻两帧图像间物体保持三轴±(5°+3°×s)旋转，s为[-1， 1]随机数。相机在距离目标1200±20 mm，半径10 mm的圆柱区域内随机移动，相机拍摄方向始终平行于光照方向。相机内参fx=fy=1650,cx=cy=300。

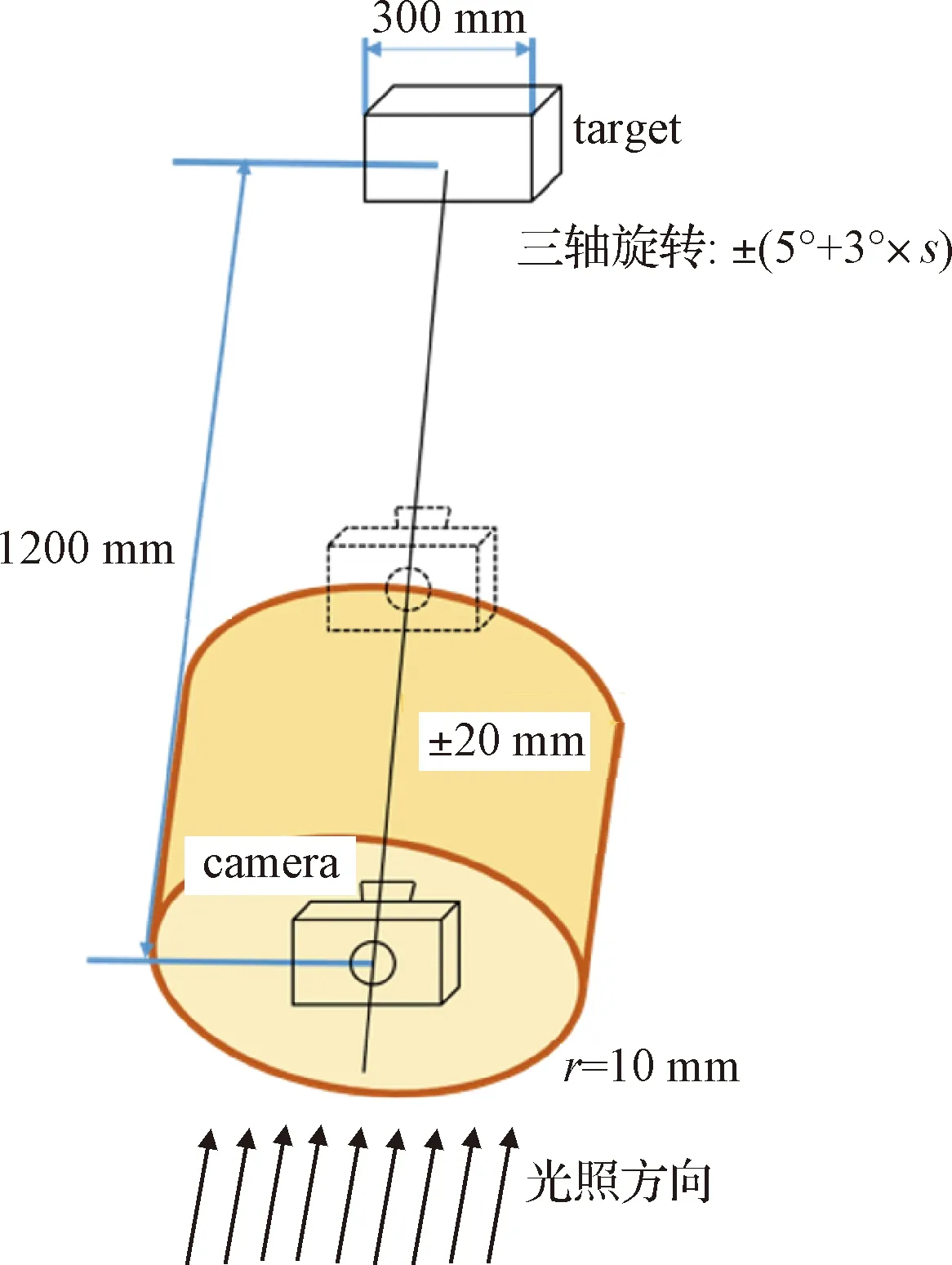
图3 图像仿真场景Fig.3 Rendering scene of image generation

对于每个模型生成1000张序列图像，部分仿真图如图4所示。

图4 仿真图像Fig.4 Examples of synthetic images

在仿真实验中，本文也进行了其他尺寸模型实验(模型缩放至400 mm、1000 mm、1200 mm)，并对应调整了相机拍摄距离以及相机参数、深度区间范围等，并未发现对网络的训练过程造成明显影响。

3.2 训练设置

图像的姿态信息通过COLMAP[12-13]稀疏重建获得，图像的深度信息由仿真过程生成。训练过程中，将微软3D库模型以及北斗卫星模型仿真图像作为深度估计网络的训练集，OSIRIS-REx和ICESat-2卫星模型作为测试集以验证在未知模型中的泛化能力。将每个模型的1000张图像，按每5张构成一个图像序列。初始学习率为0.001，采用Adam优化器，betas分别为0.9与0.999，weight decay为0。预设深度区间为750～1550 mm，分别测试了将该区间划分为128/160/192个间隔下的模型训练情况。

损失函数设置为如下：

(13)

式中：I为图像序列参考帧，H,W分别为图像的长和宽。对于图像中任意像素p，记其深度真值G(p)，通过神经网络获取其估计深度E(p)，以p∈O表示该像素位置属于观测目标，e(p)为像素深度的Smooth L1 Loss，即：

(14)

式中：x=E(p)-G(p)。

该深度估计网络在12 G显存的NVIDIA 3060上进行训练和测试，训练过程中batch固定为1，训练10个epoch。

需要注意的是，由于在图3所示的仿真场景中，光学相机观测方向与光照方向基本平行，且光照强度适当，保证了目标观测结果的完整，从而可以将目标所占像素均纳入损失函数中进行计算。考虑到空间环境的复杂性，实际观测条件下光照强度、入射方向等因素影响，导致部分像素过亮或过暗。这可能需要对部分训练参数进行调整，如：在计算损失函数时对像素进行筛选，对图像进行预处理，以及增加训练epoch数量等。

3.3 深度估计误差

为衡量神经网络模型深度估计效果，分别评估了不同间隔划分数量下测试集中所有图像序列的像素平均估计误差如表2。

表2 像素平均估计误差Table 2 Average estimating error of pixels

不同误差区间所占测试结果百分比如表3所示。

表3 估计误差区间Table 3 Error ration of each range

根据表2和表3可以看出，在深度方向划分更多的间隔并不能够保证更高的估计精度，这一现象可能源于更多的参数量引起的神经网络模型过拟合。

图5展现了部分图像序列在n=160下对于序列参考帧的深度估计结果。

图5 深度估计结果Fig.5 Examples of depth estimation

从图5可以看出，基于深度学习的深度估计算法能够对空间非合作目标中的光滑无纹理区域进行深度估计，但是对于目标部分零部件等细节区域估计结果还有待进一步提高。

3.4 表面重建结果

本文在表面重建过程中并未使用测试集卫星模型的所有图像。由于在稀疏重建过程中，特征点的位置通过大量优化过程获得，通过将特征点投影至对应图像中，评估该幅图像中对所有特征点的平均估计误差，并以此作为对图像整体估计误差的近似，通过不同的误差阈值对图像进行筛选并重建。重建过程中，设置空间中体素网格大小为3 mm，式(5)中t=6 mm。OSIRIS-REx卫星和ICESat-2卫星不同观测角度下的实际结构如图6所示。

图6 卫星实际结构Fig.6 Structures of satellite models

分别设定特征点估计误差阈值为5 mm和10 mm，获得的表面重建结果如图7所示。

图7 不同阈值表面重建结果Fig.7 Results with different error threshold

对比图6中的卫星实际结构以及图7中的重建结果，可以看出，采用较小的误差阈值进行图像筛选有利于在整体结果中突出卫星表面的细节信息，然而，更少的图像数量也会导致单个像素的估计误差难以被优化，使得重建结果不够平滑。

3.5 点云结果对比

由于传统算法难以解决纹理缺失区域导致的大量空洞，进而难以实现区域的表面重建。将3.4节中基于TSDF的表面重建结果进行抽样，生成重建点云与传统算法进行对比。

传统重建算法由COLMAP对所有1000张图像进行重建产生，得到点云结果如图8(a)。可以看出，相较于传统算法，本文所提方法有效地解决了纹理缺失区域的点云/表面重建结果完整性问题。

图8 基于深度学习算法与传统算法点云对比Fig.8 Point clouds of learning-based method versus traditional methods

通过测量卫星重建点云外形尺寸，得到重建精度如表4。模型1和2分别代表OSIRIS-REx卫星和ICESat-2卫星模型。

表4 重建精度Table 4 Reconstruction accuracy

根据表4结果，由于COLMAP对于目标重建的完整性不佳，部分情况下会导致目标外形尺寸误差较大。而通过本文方法进行重建，在保证了目标重建结果完整性的同时，也保证了较高的重建精度。

4 结 论

对于未知空间目标纹理缺失表面的重建结果缺失问题，本文设计了一种基于深度学习和TSDF的重建算法。首先通过构建神经网络，实现对序列图像参考帧中任意像素的深度估计，在训练过程中利用不同模型生成仿真图像，提高了神经网络泛化能力。其次，通过TSDF算法将图像深度信息转化为目标表面，实现了不同观测位置下的重建结果融合，提高了观测结果的完整性。根据文中进行的仿真实例，该重建算法实现了对未知空间目标的深度估计与完整表面重建，有效地解决了传统算法的表面重建结果缺失问题。