一种LSTM模型预测BC值的空间碎片无控再入预报方法

蒯家伟，赵柯昕，孙立刚，廖名传

(1. 南京航空航天大学航天学院，南京 211106； 2. 北京电子工程总体研究所，北京 100854；3. 北京遥测技术研究所，北京 100094； 4. 中国科学院微小卫星创新研究院，上海 201304)

0 引 言

低地球轨道(LEO)空间碎片在大气阻力耗散作用下，轨道能量降低并再入大气层，进而解体陨落。空间碎片再入有利于降低驻空物体(RSO)碰撞风险，维持空间环境物体数量稳定，由于其中存在大型碎片如运载火箭上面级、燃料储箱等，可能因再入大气层时燃烧不充分而撞击地面，对地面人类财产等带来安全隐患[1]，因而对空间碎片的再入时刻预报对空间环境的治理与地面安全的保障有着重要意义，为了降低这类事故风险需要对空间碎片再入时刻进行高精度的预测。现阶段空间碎片再入时刻预报误差主要来源于大气阻力的估计误差。大气阻力摄动fdrag主要与碎片的大气阻力系数Cd,面积质量比A/m,大气密度ρ和相对于大气速度矢量v有关，其表达式如式(1)所示：

(1)

式中：v=|v|，其中大气密度受太阳和地磁活动影响，存在较强的短期时变特征，较长时间预报导致轨道误差较大，因此空间碎片再入时刻精确预测一直是空间碎片研究的重点和难点[2]。

国际机构间空间碎片协调委员会(IADC)自1998年以来为了提高空间碎片再入预报水平，组织开展了27次再入陨落预报联测活动，从历史结果看总体统计精度水平在30%～10%之间[3]。在预测方法方面，通过实时卫星数据矫正密度模型提高大气密度预测值[4]，由高精度大气模型得到较精确的相对大气速度[5]等方法可一定程度上提高短期预报精度，但因空间碎片外型、材质、运动复杂多样，这类方法难以适用。空间碎片大气阻力系数和面质比参数主要受大气密度、材质、碎片姿态的影响，直接测量阻力系数和面质比参数十分困难。因此在难以确定面积质量的情形下，通常轨道预报将阻力系数和面质比耦合成一个系数，称为弹道系数(Ballistic coefficient，BC)，本文在公式中以β表示。

(2)

BC的值可以在具有雷达、光学等观测条件下通过精密定轨进行估算，从而提高再入预测精度。而当信息不充分时，要提升空间碎片再入弹道系数估算精度是很困难的。对于无观测设备、或者观测能力不足的情况下，BC的估算还可以通过机构(space-track.org)发布的两行根数进行拟合预测，这是当前IADC国际联测中各机构基于space-track.org数据的主要方法。以Pardini和Anselmo提出基于BC序贯修正预测BC值的再入时刻预测方法为例，其BC值的不确定度为±20%[6]，再入时刻预测偏差接近20%。

近年来随着人工智能(AI)技术的发展，深度学习(DL)如深度神经网络(DNN)、卷积神经网络(CNNs)、长短周期记忆神经网络(Long short term memory neural networks，LSTM)等方法被广泛应用于参数预测、建模。航天任务与空间科学中人工智能算法研究近年来也是热门课题，涉及地磁活动性指数、热层大气密度、电离层电子含量等在内的多种参量都使用深度学习法进行了较高精度地预测或建模[7]，包括与本文密切相关的对大气密度存在重要影响的参数地磁指数的预测，Kp指数[8]和Dst指数[9]都可以通过神经网络算法进行预报；Chen等[10]开发出R-DCGAN模型实现了TEC Map缺失数据的补全，以及全球预测和未来预测，受此启发，Pan等[11]设计开发了DCGAN-PB；随后，Liu等[12]和Tang等[13]也分别使用长短周期记忆神经网络预测了常态及磁暴期间电离层TEC。张君彪等[14]提出了一种基于集合经验模态分解和注意力长短时记忆神经网络的高超声速滑行飞行器轨迹智能预测方法，对气动加速度进行实时估计，进而智能预测飞行轨迹。此外在空间物体有控再入以及路径规划方面，深度学习的应用也取得了较多的研究成果，周大鹏等[15]设计了一种智能神经网络自适应复合控制方法，基于误差反馈学习准则在线更新神经网络权重以自适应提升空天飞机再入精度。相比于传统方法，深度学习可以从大量观测样本中提取有价值的特征，并利用多神经网络层重现相关特征，从而实现状态预测。

本工作提出了一种利用两行轨道根数(Two line element, TLE)数据获得精确弹道系数BC的深度学习方法，采用长短期记忆神经网络LSTM模型对其进行预测，继而利用高精度动力学模型计算再入时刻。本文首先介绍了利用简化通用摄动模型(SGP4)从TLE数据中获取精度较高BC值的算法，并实现其计算过程与结果，建立BC值训练集，然后详细阐述了LSTM预测模型结构的再入时刻预报模型的建立过程，最后对训练好的模型性能进行验证。使用LSTM模型剔除了BC值中存在的误差因素，可以在空间碎片再入前中长期获得比较准确的再入时刻。不仅如此，这种方法在一次学习之后可以快速地对大批量空间碎片再入时刻进行动态跟踪预测，提高预测精度，并可大幅减少积分计算量，显著提升运算效率。

1 弹道系数的计算

1.1 TLE数据的预处理

TLE数据中包含了空间碎片的轨道根数、平运动以及和大气阻力相关的B*数据。在大批量使用TLE数据时，大概率会遇到空间碎片TLE数据异常情况，包括重复历元、数据格式错乱、编号异常等。因此需要对整个TLE数据进行预处理，以去除异常和错误的数据[16]。预处理过程主要包括去除重复TLE数据、平均运动项异常数据、倾角异常、B*为负值的数据等，由于TLE格式可读性问题，预处理过后的TLE数据依然会存在某些异常情况，会明显反应在后续计算结果中。

1.2 弹道系数BC估计方法

以Saunders等[17]和Gondelach等[18]提出利用TLE数据修正BC值的方法作为本文研究的比对基准。其基本原理是通过利用TLE配套的SGP4模型从TLE数据中获得碎片的轨道状态、物理参数(特别是B*数据)等信息，建立连续TLE数据间的平运动参数变率迭代估计任意时刻的BC值。

由于TLE数据中不包含短周期项的变化，数据中半长轴的变化可以假设为仅受大气阻力影响下的长期项变化。考虑到太阳光压导致的半长轴长周期变化可能包括在TLE数据中，但由于太阳光压与低轨卫星再入过程中大气阻力摄动相比，其影响要小得多，因此本文忽略光压的影响。由此可假设基于TLE数据平运动参数计算得出的结果与由轨道外推计算结果之间的任何差异都是因为大气阻力弹道系数BC值的不正确猜测引起的。利用连续TLE数据计算BC值的过程如下：

1)利用TLE数据中的平运动参数计算两个TLE数据的半长轴的变化量Δa。

(3)

Δa=a2-a1

(4)

式中：a为轨道半长径；μ为地球引力常数；n0为空间物体轨道平均轨道运动速度，也就是TLE的平运动项。a1与a2分布表示前后两次TLE数据的半长径。

2)使用高精度的轨道动力学模型进行外推，计算两个TLE时刻(tTLE1,tTLE2)内仅由大气阻力引起的轨道半长轴的变化。其中p为轨道半通径，θ为真近点角，e为偏心率，p=a(1-e2),fRdrag,fTdrag分别是由阻力在径向和横向分量产生的加速度。

(5)

(6)

3)利用TLE数据中的B*参数确定BC的初值。B*参数是SGP4模型中的近似反应阻力的系数，可以通过(7)式计算得到BC的初值β1。第二个TLE根数的BC值β2可以通过第一个BC的值β1和Δaprop之间的线性关系计算得到。当Δaprop小于10-4千米时，BC值收敛。如果在后续计算过程中出现了过早再入的情况，可以将β1的值设置为原来值的90%，但是需要更多次的迭代方能收敛。

(7)

4)对BC值进行迭代计算，直到迭代收敛。βn是迭代过程中第n个BC值。

(8)

式中：Δadiff=Δa-Δaprop。

在默认情况下，使用正向传播来进行BC值的估算，取最早TLE时刻的状态，将它外推到最新TLE数据时刻的状态。也可以使用反向传播，从最新的TLE时刻的状态向后传播到前一个TLE时刻的状态，反向传播可以防止预测时空间碎片过早的再入。在临近再入时刻估计时十分有用，因为不准确的BC估计值可能导致再入预报异常。以上估计过程其本质原理类似Newton-Raphson方法。如果TLE数据充分，且TLE数据在时序上连续且间隔不大，不失为一种较优的方法，然后对于中短期预报来说，由于其数据使用率较高，如果其中出现异常点，其预测值会突然拉偏，导致预报误差突然增大。空间物体的轨道是摄动情况下连续可微的拟二次曲线，因此有必要在预测过程中考虑短期的数据情况的变化，同时又能兼顾长期的动力学演化趋势，因此本文参考了长短期记忆网络预测模型LSTM在空间任务中的研究结论，将其应用于弹道系数BC值的预测。

2 长短期记忆神经网络LSTM模型原理

为了解决原有的循环神经网络(RNN)存在梯度爆炸或梯度消失的问题[19]，Hochreiter等[20]于1997年提出了长短期记忆神经网络LSTM，并被Graves等[21]进行了改进和推广。LSTM神经网络经过了特殊的设计，使得其适合在重要事件之间存在很长时间滞后时从经验中学习，以对时间序列进行分类、处理和预测，目前在多个领域得到了广泛的应用，其单元内部包含遗忘门、输入门和输出门，具体结构如图1所示。

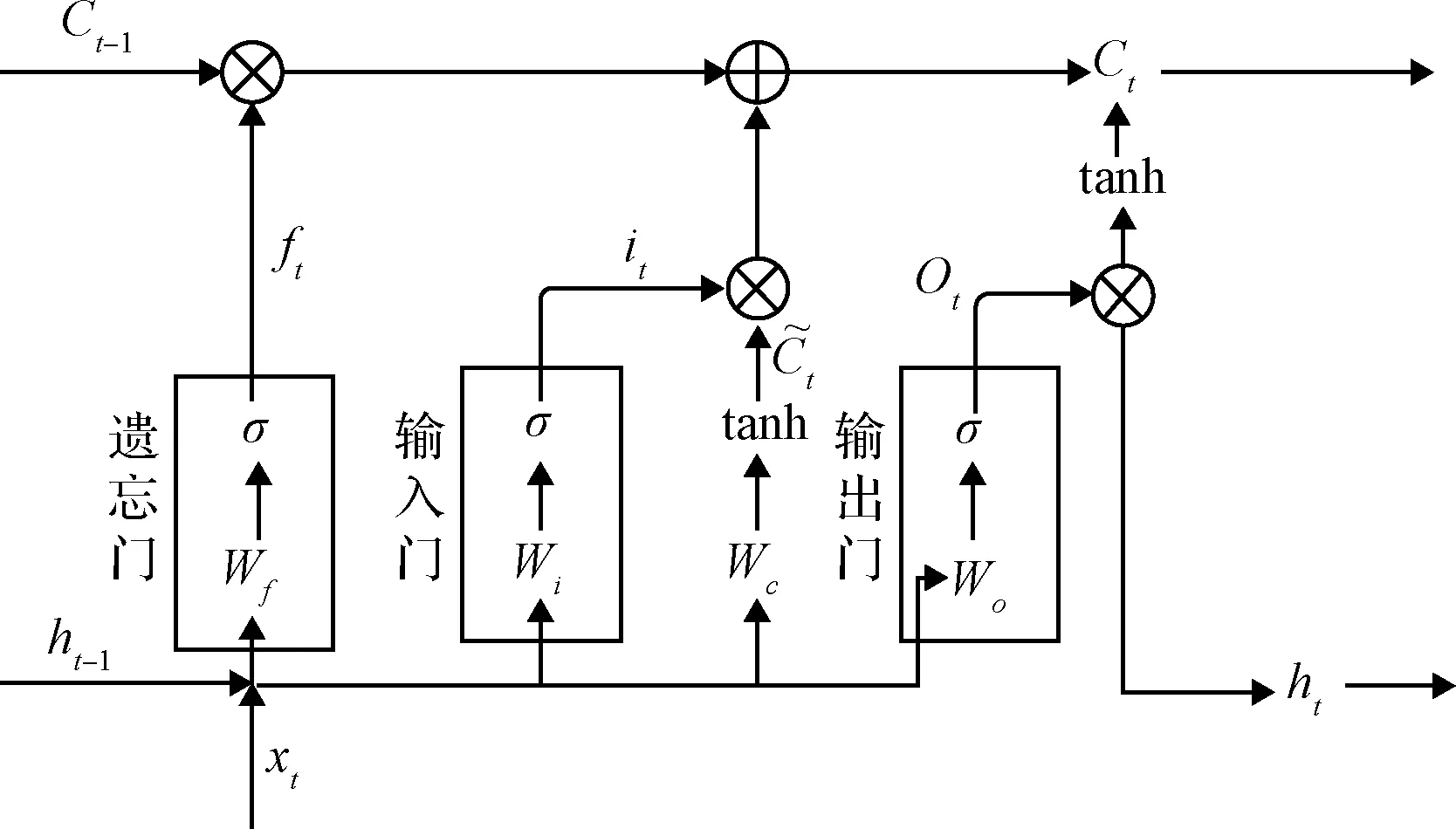
图1 LSTM单元内部结构Fig.1 Internal structure of LSTM unit

遗忘门用来确定状态传递的过程中上一时刻的单元状态ct-1有多少保留到当前时刻的状态ct。读取上一个时刻输出值ht-1和当前时刻输入的BC值数据xt，并利用设定的连接权重矩阵Wf和sigmoid函数σ计算得到经过处理的需要保留下来的历史信息状态，如式(9)所示，其中bf为遗忘门的偏移值。将会输出一个0至1之间的数值给历史状态ct-1，1表示完全保留，0表示完全遗弃。

ft=σ(Wf[ht-1,xt]+bf)

(9)

输入门利用连接权重参数Wi、偏移值bi等参数来确定当前时刻输入的BC值数据xt有多少可以作为输入门的输出it，如式(10)所示。再利用计算新状态的连接权重矩阵WC、偏移值bC确定临时的当前时刻新状态，如式(11)。再利用遗忘门和输入门的数据更新状态，将上一时刻状态ct-1更新到当前时刻状态ct，如式(12)。

it=σ(Wi·[ht-1,xt]+bi)

(10)

(11)

(12)

输出门利用连接权重矩阵Wo、偏移值bo确定当前时刻的输出值ht，如式(13)、式(14)所示。

ot=σ(Wo[ht-1,xt]+bo)

(13)

ht=ot·tanh(Ct)

(14)

3 再入预报流程与性能评估

3.1 再入时刻预测流程

首先建立预测模型的训练数据集，别选取近三年再入大气层的80个和20个空间碎片的TLE数据作为预测模型的训练集和测试集。TLE数据和再入时刻都是从北美防空司令部空间目标监视编目轨道根数发布网站(https://www.space-track.org)上获取的，该网站发布了空间物体历史TLE数据以及再入日期，确切的再入时刻未给出，因此最终再入时刻仅能精确到天。

LSTM模型预测弹道系数BC值的具体流程如图2所示。首先对所有TLE数据进行预处理，剔除其中误差较大及错误的数据，利用1.2节的方法计算出每一TLE时刻的BC值，随后将得到的BC值随时间变化数据代入LSTM模型，确定模型中的特征参数，由此得到了BC值的精确预测模型，再将测试集代入预测模型中，得到对未来BC值的预测，即可计算出精确的再入时刻，最后对再入时刻进行评估。

图2 空间碎片再入时刻预测流程Fig.2 The reentry time prediction scheme of space debris

3.2 弹道系数BC的估计

图3为编号为32712的空间碎片再入大气层前200天分别利用1.2节所述的迭代过程和由TLE数据中B*参数两种方法计算得到的BC值随时间的变化曲线。图中横轴为再入前的时间，纵轴为BC值的大小。图示TLE数据是经过预处理的，可以看出两种方法计算的BC值具有相同的变化趋势，但是有一个偏移量，同时BC值中仍然存在一些异常点，如果进一步利用近地点半径进行滤波，这些异常值会被剔除。

图3 编号32712空间碎片BC值与再入时刻关系Fig.3 The relationship between BC value and reentry time of the space debris No. 32712

利用1.2节的迭代方法，选取了100个已再入陨落的空间碎片作为目标集，计算了目标集对应的从再入前200天到再入时刻弹道系数BC的最小值、平均值和最大值。计算结果表明基于迭代修正的BC值预测再入时刻精度在10%的置信度为60%～70%，预测精度在20%的置信度为95%。根据欧洲航天局的DISCOS数据库提供的信息，弹道系数BC估计值精度20%的置信度为85%。考虑到大气密度10～20%误差因素，表明BC可以利用1.2节的流程建立训练集。因此以此为参考对象建立训练集样本，利用LSTM模型预测BC值，进而预报再入时刻，并评估预报精度与模型性能。

3.3 建立预测BC值的LSTM模型

LSTM模型的建立主要分3个步骤：首先需要对BC值数据集进行整理；其次是完成对模型的构建，包括确定用于训练和预测所需要的特征参数和确定LSTM神经网络模型的具体参数；最后是利用测试集数据代入得到预测结果，并对预测模型准确性进行验证,如图4所示。

图4 LSTM预测模型框架Fig.4 The framework of LSTM prediction model

采用多时刻输入单一时刻输出的模式对弹道系数BC值进行预测，利用40天的TLE数据作为预测模型的输入，预测结果作为输出。设置两层LSTM预测模型，并使用全连接层对LSTM层进行线性化。训练过程中，反向传播的误差项是损失函数对输出值的倒数，损失函数是均方根误差函数，给定各层神经元个数、学习率以及训练迭代步数，利用梯度下降算法更新网络权重并获得最终的隐藏层。随后将测试集进行迭代预测，并输出预测结果。

建立弹道系数预测模型时需要考虑5个参数，即训练步长、输出层维数、隐藏层层数、隐藏层维数和输出变量维数。训练步长的设置要考虑该步长包含的信息量是否可以满足模型训练，若设置的过小，则不足以使模型在训练中学习BC数据的变化规律，同时考虑到模型训练难易程度，设置过大可能使得数据序列中包含过多无用数据，导致预测性能下降并增加训练时间。本工作测模型中训练步长设置为20步。

针对于本文的陨落时间预测场景，输入层维数的设置根据双行轨道根数中轨道和动力学特征数据来确定,在本模型中使用TLE数据,所以输入层维数设置为1。多隐藏层的网络从理论上来说有足够的表达能力可以拟合任何复杂的函数,但网络结构越复杂越难以训练,并且可能出现过拟合的情况,即在训练数据上表现很好,但泛化能力差。隐藏层维数即为隐藏层神经元个数,对于较复杂、非线性程度大的序列,设置的神经元个数越多拟合效果越好,但花费的时间也越多,同时可能出现过拟合的现象。本模型中隐藏层由两层LSTM层和全连接层构成,第二层的LSTM层神经元个数是第一层个数的两倍，第三层的全连接层神经元个数和第一层LSTM层个数相等，由于本文主要是利用算法，算法具体细节不作赘述。

3.4 LSTM预测模型的性能评估

使用平均绝对百分比误差(MAPE)作为评估参数与预测模型输出值之间的预测准确性度量，用以量化训练后预测模型的性能。MAPE定义为测试数据集中每个数据点上的BC预测值βpre与计算值βcal之间的真实误差之和与计算值βcal之和的比值，下式中以ξ标志，其数学表达式为：

(15)

式中：n是参与训练的有效数据数量。利用预测模型预测出结果越精确，式(15)将越逼近其下边界0，MAPE的数值越低说明预测模型的性能越好。这里选择的度量标准与预测模型的目标一致，该目标是通过最大程度减少训练数据中的总误差，使所有数据点尽可能平滑。

3.5 LSTM模型预测BC值效能分析

采用编号20230的空间碎片，利用其再入前200天至160天之间40天的TLE数据作为预测模型的输入，预测再入前160天的BC值随时间的变化关系。

图5横轴表示再入预报所用TLE根数时间与www.space-track.org公布的再入时间的间隔，即当前历元距离再入日期的天数，从再入前160天至再入时刻为止，纵轴表示了BC值的大小。其中橙色折线的中心点表示了10天内的BC计算值的平均值，蓝色折线的中心点表示了10天内的BC预测值的平均值，误差线表示了10天内的最大值和最小值。总数据统计预测模型的性能指标MAPE达到13.9%，在某些时间段，MAPE更低，其中有一些未能预处理掉的异常数据点也清晰地反映在图上,如果剔除一些异常点，预测结果的MAPE值会更低。数据结果表明训练好的预测模型可以较好地学习BC值变化趋势，表明本文建立的LSTM预测模型是有效的。

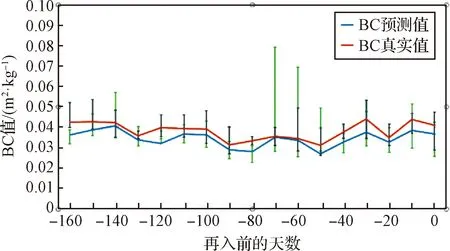
图5 编号20230的空间碎片再入前160天的BC预测值和计算值与预测时间的关系Fig.5 The relationship between BC predicted/calculated values and predicted times for 160 days prior to reentry of the space debris No.20230

3.6 再入预报能分析

BC值预测的目标是为了更好地预报空间碎片再入时刻，或者是在轨寿命。在获得BC预测值之后，基于最新的TLE根数，考虑地球非球形摄动、大气阻力摄动、太阳光压摄动和日月三体引力摄动，利用RKF7/8阶数值积分进行轨道外推，外推截止轨道高度设定80 km即认为目标已经发生了再入，采集此时的历元作为再入时刻。

为了评估再入时刻的预报精度，使用时间的相对误差估计的精度，再入预报精度ε定义为实际预测时间误差与最后所用轨道根数历元距离陨落日期的时间之比值。

(16)

式中：tpre是预测的再入日期,tact是space-track.org网站上公布的再入日期,tTLElast是最后用于预测再入时刻的TLE轨道根数历元。

以编号42727目标为例，取再入前160天内所有有效的TLE数据，利用当天的TLE数据计算出卫星的状态，并预测出从TLE数据时刻到再入时刻的BC变化趋势。利用卫星轨道参数和BC变化计算出卫星再入时刻并与space-track.org网站给出的真实时刻计算再入时刻误差，如图6所示。可以发现，利用本文方法得到平均预报误差为7.3%，再入前160天时预测误差在4%以下，再入前30天时预测误差在10%以下。但是再入前20天预测的效果没有长期预测的理想，最大预测误差可达到51%，这是因为space-track.org给出的目标再入时刻只精确到天，依据式(16)的标准，越到末端误差会急剧增大，导致即使预测是准确的，再入前10天预测时每差24小时就带有近10%的误差，再入最后2天每一至两个小时就接近10%误差。同时，短期预测误差率大也可能是因为接近再入大气层时气动力快速变化导致无法准确预测与计算，因此后续评估主要对大于30天临近再入时间的再入预报有较好的指导意义，但本文同时也给出了小于30天的预测结果。

图6 编号42727空间碎片再入时刻预报结果Fig.6 Re-entry time forecast results of the space debris No.42727

选取5个已再入物体作为测试目标，利用本文的方法预测其再入前160天至再入时刻的BC变化，基于再入前160天，90天和30天的TLE数据计算再入时刻，并计算再入时刻误差。计算结果如表1所示。

表1 测试目标再入时刻预报结果Table 1 Re-entry time forecast results of the test targets

对选取的90个目标于再入前10天、20天、30天、60天、90天和160天时预测再入时刻并得到累计误差。所得到的再入预报时间累积误差和95%置信区间结果如图7所示。图7表明，再入前160天时的预测最准确，总误差低于5%，再入前10、20天预测的结果不如整体结果准确是由于公布的再入时刻精确到天导致。总体来看，再入前160天，90天，30天分别得到的预测误差在5%以下，8%以下和12%以下，算例表明利用长短期记忆神经网络先预测出物体BC变化规律再进行再入时刻预报可以得到较好的空间碎片无控再入预报时刻。

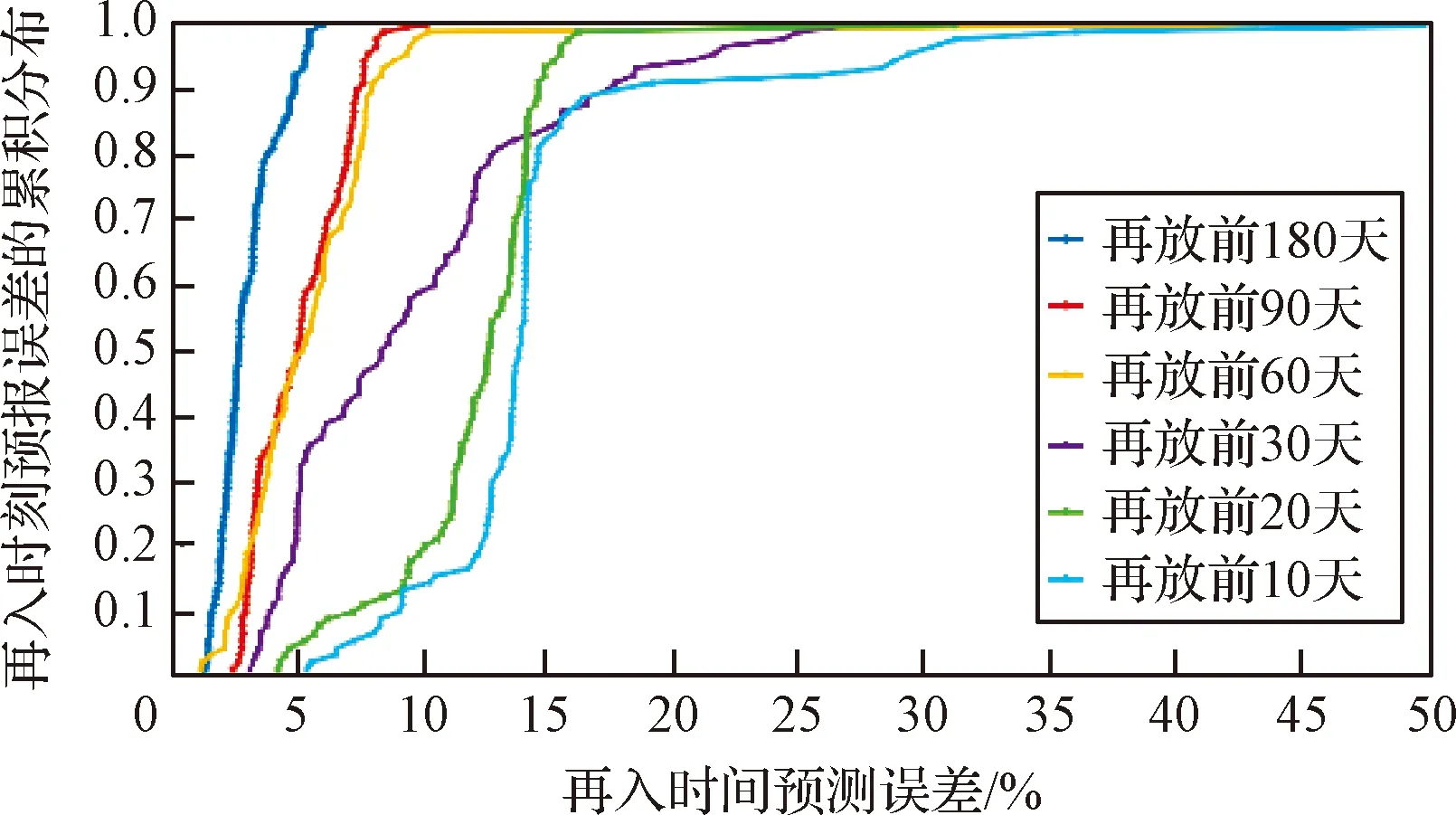
图7 90个目标的再入前10、20、30、60、90和160天的再入时刻预报误差的累积分布Fig.7 Cumulative distributions of reentry time prediction errors of 90 objects for 10, 20, 30, 60, 90, and 180 days prior to reentry

4 结 论

空间碎片无控再入时刻预报是一项国际上非常关注的重要工作，其受到大气密度、轨道数据精度、弹道系数估计等诸多因素的制约，以至于准确预测空间碎片的再入时刻是十分困难的。在已有大气阻力弹道系数BC值预测方法的基础上，建立了基于长短期记忆神经网络深度学习LSTM模型预测BC值，进而预测空间碎片再入时刻的方法，获得了较好的研究结果。从选取的样本训练模型以及测试结果看，在95%的置信度内，90天预测精度达到8%，30天预测精度达到12%，考虑到大气密度模型带来的不确定影响，结果表明LSTM模型预测方法在空间碎片再入预报具有很好应用价值。后续我们将进一步精细化考虑空间碎片类型，将相近类型的空间碎片进行聚类，建立更精确数据样本，提高再入或者在轨寿命预测精度。