观测轮廓显著性耦合时的轨道根数反演方法

2022-02-01苏剑宇方海燕高敬敬

宇航学报 2022年12期

苏剑宇，方海燕，高敬敬

(西安电子科技大学空间科学与技术学院，西安 710126)

0 引言

作为深空网络(Deep space network，DSN)的补充和替代技术，X射线脉冲星导航(X-ray pulsar-based navigation，XPNAV)是一种新型的自主导航技术。XPNAV可为在太阳系内外飞行的航天器提供位置、时间等导航信息[1-4]，实现航天器高精度自主导航。目前，随着X射线探测器技术的不断进步，国内外相继开展了X射线脉冲星导航试验。如中国空间实验室天宫二号的γ暴偏振探测科学实验[5]，中国首颗X射线脉冲星导航试验卫星(XPNAV-1)在轨开展的X射线脉冲星的探测与脉冲星导航体制的验证[6-8]，以及国内首颗空间X射线天文硬X射线调制望远镜卫星(Hard X-ray Modulation Telescope，HXMT)Insight-HXMT的脉冲星定轨精度验证实验[9-10]。国外的如美国NICER(Neutron star interior composition explorer)项目的SEXTANT(Station explorer X-ray timing and naviga-tion technology)搭载在国际空间站(ISS)上开展的定轨精度验证工作[11-12]。

现有XPNAV导航验证的主要框架可分为两种类型：实时和非实时[13]。前者利用脉冲星观测周期内记录到的一串光子到达时间(Time of arrivals，TOA)，通过一定的算法提取出脉冲相位以及多普勒频率，由于航天器在任意时刻观测的脉冲相位和频率都可以用该时刻的位置、速度以及太阳系质心(Solar system barycenter, SSB)处的脉冲星信号模型准确地表示，因此通过对相位与多普勒频率的解算即可得到相应时刻的位置与速度信息[14-16]。如SEXTANT任务通过对多个毫秒脉冲星的观测数据进行处理，得到10公里以内的导航精度[17]。文献[18]在XPNAV-1的轨道传播中引入脉冲星视线相对于地球的测距测量作为控制点，通过对脉冲星PSR B0531+21近三个月的观测，在控制点进行自我定位，平均导航误差为38.4公里。

根据以上分析，SEPO方法是一种离线确定轨道根数的方法，该方法利用观测轮廓的形变确定轨道根数，而非脉冲TOA，因此不依赖脉冲星标准轮廓，有助于应用到不同的任务场景中。但是这两个导航实验只考虑了单个轨道根数存在误差的情况下轨道根数的反演，实际中轨道根数可能都存在误差，此时得到的观测脉冲轮廓显著性会产生耦合，无法直接通过观测脉冲轮廓显著性的极大值确定轨道根数的最优估计值，如何在观测轮廓显著性耦合情况下进行轨道根数的反演并未进行讨论。文献[13]在SEPO方法的基础上提出显著性卡方分组的思想解耦显著性卡方，并通过对分组后的显著性卡方再次计算二次卡方确定轨道根数的最优估计值。该方法的显著性卡方分组的思想为解耦显著性卡方提供了思路，但该文献方法仍然使用二次卡方的最大值确定轨道根数的最优估计是不合理的，因为显著性卡方反映了轮廓的显著性，在轨道真值附近取极大值，但二次卡方与观测轮廓并无直接关系，所以二次卡方最大值并不一定对应轨道根数的最优估计值，这将导致轨道根数估计值偏离真值；且在逐一估计得到轨道六根数的过程中，本次的轨道根数估计将会影响下一轨道根数的分组，所以本次轨道根数的较大估计误差将导致下一轨道根数产生更大误差。

综合以上分析，上述文献方法虽然可在单个轨道根数存在偏差时，根据观测轮廓显著性反演轨道根数，但无法在轨道六根数均存在偏差时，即观测轮廓显著性耦合的情况下实现轨道根数反演。针对该问题，本文研究了显著性数据的分布特征，并根据其分布特点，提出利用该数据的方差这一数字特征作为轨道根数最优估计的依据，实现观测轮廓显著性耦合情况下的轨道六根数的估计，并利用实测数据验证了方法的有效性。

1 显著性耦合下的轨道根数反演方法

图1 显著性耦合下的轨道根数反演方法Fig.1 Flow chart of the orbital elements inversion method for significant coupling

1.1 轨道动力学模型

将航天器视为质点，在J2000.0地心惯性坐标系(ECI)下，如图2所示坐标系OXYZ。航天器的轨道动力学模型可表示为

(1)

式中：r与v分别为航天器的位置和速度；a为航天器的加速度。航天器在轨道上运动要受到各种力的影响，产生的摄动加速度是多方面的。为避免定轨过程中计算量过大，建立如下的近地轨道卫星的预测模型，该模型由如下加速度项组成。

a=aTB+aNS+aS+aM+aD+aSP

(2)

式中：aTB为航天器所受到的地球二体引力加速度；aNS为地球非球形摄动加速度；aS与aM分别为太阳引力与月球引力的摄动加速度；aD为大气阻力摄动加速度；aSP为太阳光压摄动加速度。表1给出了文中使用的动力学模型中摄动力计算使用的模型名称，计算公式可参考文献[20]。

表1 轨道动力学模型Table 1 Descriptions of orbital dynamics models

轨道六根数分别为半长轴a、偏心率e、升交点赤经Ω(RAAN)、轨道倾角i、近地点幅角ω和真近点角θ。

描述航天器运动最方便的坐标系之一是近焦点坐标系，如图2中坐标系Oxyz，该坐标系的基准面是航天器的轨道平面，原点为地球质心，x轴指向近地点，z轴沿航天器角动量方向，y轴与x轴、z轴构成右手直角坐标系[21]。在近焦点坐标系中，航天器的位置和速度矢量可通过轨道六根数来计算，表示为式(3)与式(4)[20]。

图2 坐标系示意图Fig.2 Schematic diagram of the coordinate system

(3)

(4)

(5)

式中：坐标变换矩阵Q为[21]

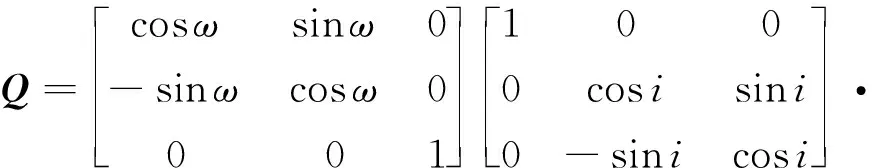
(6)

1.2 观测脉冲轮廓获取

1.2.1光子TOA校正

X射线脉冲星信号微弱，只能以光子的形式被探测器收到，由于引力、相对论等效应的影响，在获得观测脉冲轮廓之前，需要对接收到的光子TOA进行校正。对脉冲单星来说，只需转换到太阳系质心(SSB)处即可。文中使用时间转换公式如下[22]

tSSB-tsc=ΔC+ΔR+ΔE+ΔS

(7)

式中：ΔC为时钟校正；ΔR为Roemer延迟，表示光子在真空中从航天器到SSB的传播时间；ΔE为Einstein延迟，是由太阳系内天体的运动所引起的引力红移及时间变慢效应；ΔS为Shapiro延迟，由天体引力引起的时空弯曲矫正。由于时间转换项完整的表达式非常复杂，文中采用如式(8)所示的简化公式，式中的各变量均在太阳系质心惯性坐标系下表示，该模型忽略了视差、脉冲星自行以及除太阳外的其他天体的Shapiro延迟等项，转换精度为5～8 μs[23]。

(8)

式中：第一项为Roemer延迟，第二项为Einstein延迟，第三项为太阳Shapiro延迟。n为脉冲星在太阳系质心坐标系下的单位方向矢量；rsc/ssb为航天器相对于太阳系质心的位置；rsc/E为航天器相对于地球的位置；vE为地球的速度；rsc/sun为航天器相对于太阳的位置；c为光速；μs为太阳引力常数；P是周期项,可表示为[24]

P≈0.0016568sin(35999.37T+357.5)+

0.0000224sin(32964.5T+246)+

0.0000138sin(71998.7T+355)+

0.0000048sin(3034.9T+25)+

0.0000048sin(34777.3T+230)

(9)

式中：T=(JD-2452545.0)/36525, JD为儒略日。

1.2.2观测脉冲轮廓获取

利用式(8)将探测器探测到的光子TOA进行时间校正后，为获得观测脉冲轮廓，还需要将光子TOA转换为光子到达相位，使用时间相位模型可完成转换，时间相位模型如式(10)所示[15]。

(10)

式中：下标0表示在参考历元t0时刻的自转和相位参数，φ0即t0时刻的初始相位，自转频率k-1阶偏导数ν(k-1)是待拟合的参数，k=1时，ν(0)=ν0，即t0时刻的初始自转频率。式(10)相当于对脉冲周期的标准化处理，一个脉冲周期对应的相位区间长度为1。

假设观测周期为Np个脉冲周期，即光子到达相位序列可划分为Np个长度为1的相位区间。将每一个相位区间划分为Nb个等长度的片段，且将获得的光子到达相位序列折叠到相位区间(0,1)内的Nb个等长度片段，用第i个片段的中心φi表示该片段内的光子到达相位。通过对相位区间(0,1)的每一个片段内的光子数进行统计，可得到平均观测脉冲轮廓，如式(11)所示。

(11)

式中：Ci表示折叠后相位区间(0,1)内的第i个片段内的光子总数；cj(φi)表示第j个相位区间内第i个片段内的光子个数。将式(11)表示的观测轮廓进行归一化处理，如式(12)所示。

(12)

1.3 显著性耦合下的轨道根数反演方法

(13)

(14)

n=1,2,…,Na

(15)

(16)

(17)

将上述过程重复进行，依次可获得Ω,i,ω的估计值，如式(18)，(19)与(20)所示。

(18)

(19)

(20)

(21)

2 仿真校验

2.1 仿真条件

选用RXTE卫星的PSR B0531+21脉冲星实测数据包95802- 01- 16- 02，95802- 01- 16- 03与95802- 01- 16- 04，对RXTE卫星进行导航实验，脉冲星参数如表2所示。

表2 脉冲星参数Table 2 Pulsar parameters

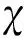
表3 初始轨道参数Table 3 Initial orbit parameters

表4 轨道根数的偏移量Table 4 The bias of the orbital elements

本文仿真实验使用的计算平台为MATLAB，计算机硬件平台为DELL T96LKJ4工作站，仿真实验使用16个线程并行运算，计算耗时约4 h。

2.2 仿真结果与分析

2.2.1耦合情况下的显著性卡方

图3 轨道六根数均存在误差时的显著性卡方值Fig.3 Significance chi square values for deviations in six orbital elements

2.2.2耦合情况下的轨道根数反演

图4 分组卡方值的统计结果(根据轨道半长轴分组)Fig.4 Statistical results of grouped chi square values (Grouped according toorbit semi-major axis)

图5 分组卡方的方差(根据轨道半长轴分组)Fig.5 Variance of grouped chi square values (Grouped according to orbit semi-major axis)

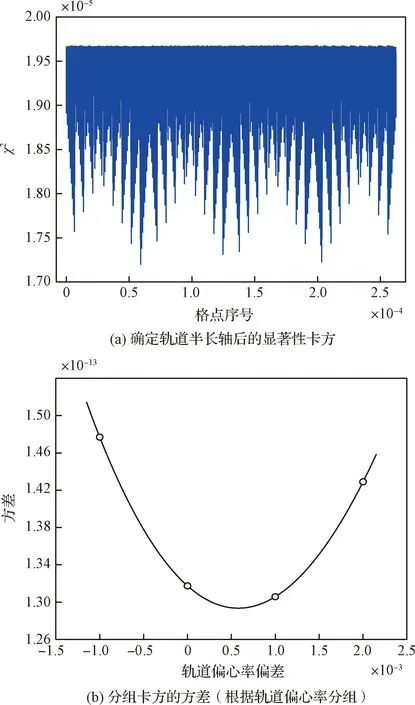
图6 轨道偏心率的搜索过程Fig.6 The search process of orbit eccentricity

图7 确定轨道偏心率后的显著性卡方Fig.7 Significance chi square after determining orbit eccentricity

图8 升交点赤经的搜索过程Fig.8 The search process of RAAN

图9 根据轨道倾角分组的卡方方差Fig.9 Variance of chi square grouped according to orbital inclination

轨道倾角确定后，只有近地点幅角ω与真近点角θ两个轨道根数耦合。图10为根据近地点幅角分组的卡方方差，通过对方差曲线拟合，并取方差最小值对应的近地点幅角，可得到近地点幅角的估计值。

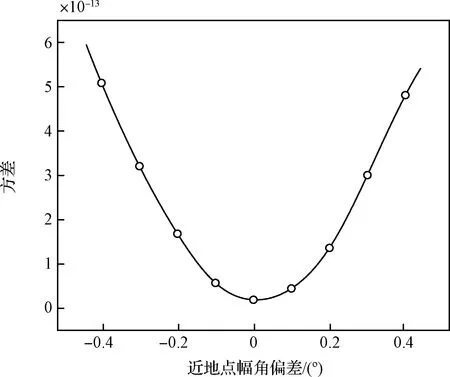
图10 根据近地点幅角分组的卡方方差Fig.10 Variance of chi square grouped according to argument of perigee

图11 确定近地点幅角后的显著性卡方Fig.11 Significance chi square after determining argument of perigee

通过上述过程，可逐一搜索得到轨道六根数，为避免脉冲星观测数据的随机性对本文方法实验结果的影响，在相同条件下，多次仿真光子到达时间序列，并利用每一组光子数据反演轨道根数，计算轨道根数的搜索误差。重复进行100次仿真实验，每一次实验可获得一组轨道根数，并计算得到轨道根数的估计误差。图12给出了每个轨道根数搜索误差的统计图，对每个轨道根数的所有实验结果取平均值，以此作为轨道根数的估计误差，如表5所示，给出了轨道根数的平均估计误差及对应的位置、速度误差。

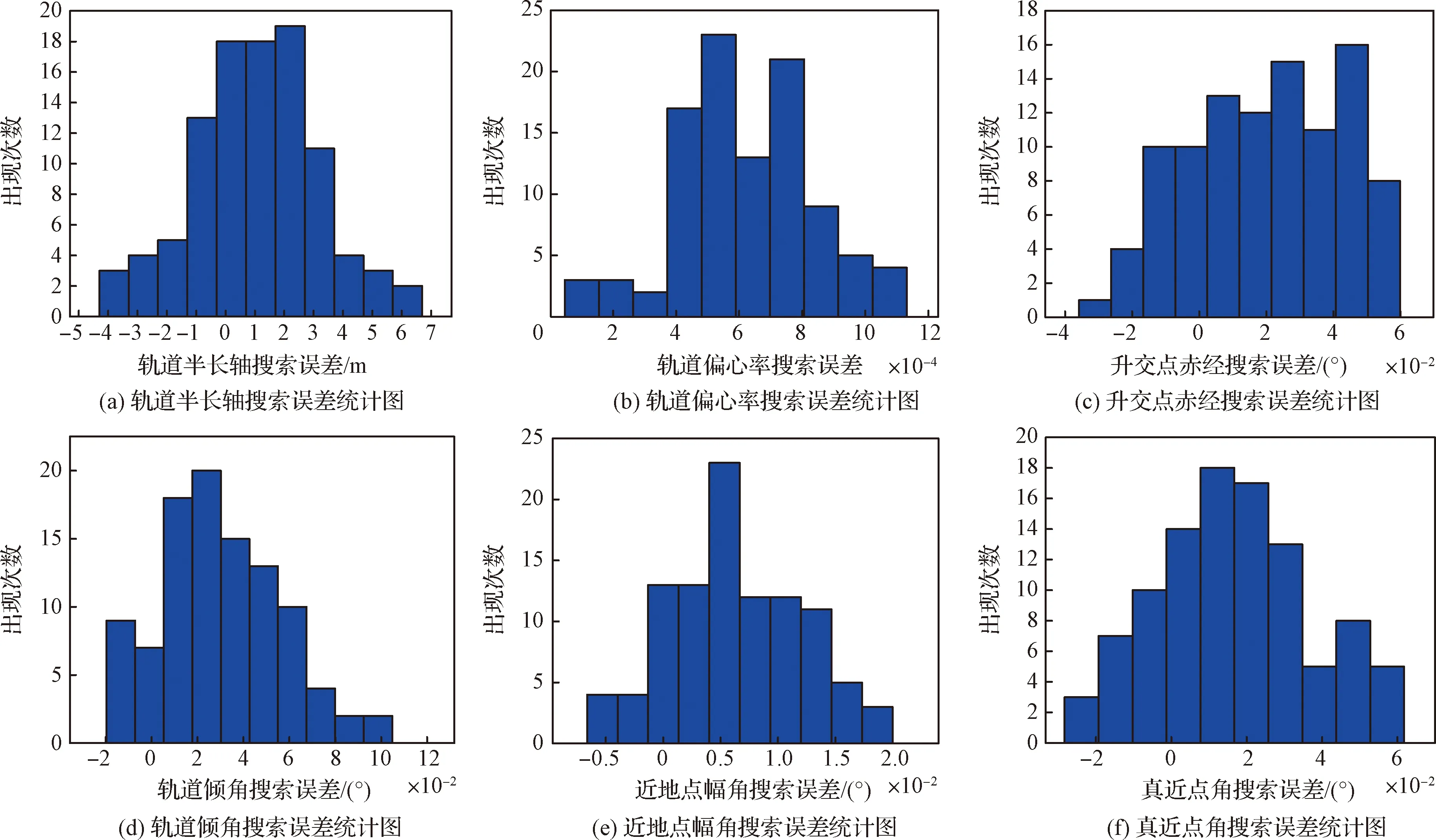
图12 轨道根数搜索误差的统计结果Fig.12 Statistical results of searching error of orbit elements

表5 轨道根数估计误差Table 5 Estimation errors of orbital elements

在相同的实验条件下，比较本文方法的搜索结果与利用文献[13]方法得到的轨道根数搜索结果，如表6所示。根据表中结果，只有真近点角的搜索误差与本文的结果是一样的，其他轨道根数的搜索误差很大，这是因为在搜索真近点角时，其他轨道根数已经搜索出结果，此时变为单个轨道根数的搜索问题，证明文献[13]的方法主要适用于单个轨道根数的搜索问题，不适用于轨道六根数同时存在误差的情况。