迎角受限的高超声速飞行器固定时间鲁棒控制
2022-02-01董泽洪李颖晖吕茂隆赵子龙裴彬彬
董泽洪,李颖晖,吕茂隆,赵子龙,裴彬彬
(1. 空军工程大学航空工程学院,西安 710038; 2. 空军工程大学研究生院,西安 710038;3. 空军工程大学空管领航学院,西安 710051; 4. 荷兰代尔夫特理工大学电气工程、数学和计算机科学学院,代尔夫特 999025)
0 引 言
高超声速飞行器(Hypersonic flight vehicle,HFV)因其飞行速度快、机动性强、突防能力好等特点,具有重要的军事价值和民用价值,受到国内外学者的广泛关注[1-5]。但由于HFV具有强非线性、强耦合、非最小相位的特性,且面临复杂快时变的飞行环境、大飞行包线内实际的气动参数与地面风洞/仿真所得的气动参数存在偏差等原因,HFV的飞行控制系统必须具备快速反应能力、鲁棒性和抗干扰能力[6-7]。另外,超燃冲压发动机的工作状态与迎角的大小密切相关,迎角必须满足一定的约束[8]。因此,HFV的飞行控制系统设计是一个重要而极具挑战性的课题。
为了应对高超声速飞行器模型不确定的问题,鲁棒控制[9-10]、滑模控制[11]、神经网络控制/模糊控制[12-13]等方法被提出。这些方法虽能处理模型不确定HFV的控制问题,但它们忽略了闭环系统跟踪误差的收敛速率。对于具有非最小相位特性、高动态、高机动性的HFV,跟踪误差的收敛速率弥足重要,误差收敛的慢不仅会影响系统的控制性能,严重时还会导致系统失稳[14]。为了提高HFV系统跟踪误差的收敛速率,减少跟踪误差的收敛时间,有限时间稳定定理被应用到HFV跟踪控制器的设计中,在指数收敛控制器的基础上增加了关于跟踪误差的分数幂次项(幂指数在0到1之间)[15-17]。然而,有限时间控制器的误差收敛时间与系统的初值有关,在系统初值不能被准确获悉的情形下,难以准确计算跟踪误差的收敛时间。为了解决收敛时间的初值依赖问题,固定时间跟踪控制器被提出,它在有限时间控制器的基础上又增加了一个关于跟踪误差的分数幂次项(幂指数大于1),使得跟踪误差的收敛时间不依赖于系统初值[18-20]。有限时间控制器和固定时间控制器在提高系统收敛速率的同时,也会带来一些问题,例如控制律中关于跟踪误差的分数幂次项(幂指数在0到1之间)求导时,产生跟踪误差的负次幂项,在跟踪误差等于零时,这一项将会变得无穷大,造成闭环系统的崩溃,即所谓的奇异值问题。因此,在设计固定时间控制器时应避免奇异值问题。
从实际角度看,超燃冲压发动机推进系统的工作状态对高超声速飞行至关重要,而超燃冲压发动机推进系统的工作状态与高超声速发动机的迎角密切相关。在一定的迎角范围内,超燃冲压发动机涵道才能获得足够的进气量,从而保证超燃冲压发动机稳定、有效地工作[8]。为了在全飞行包线内将迎角限制在一定范围,文献[8]和[21]提出了一种基于障碍函数的HFV迎角受限控制器,然而仅考虑了对称时不变的迎角限制,在设置限制时也只能设置为最小的迎角限制,在全飞行包线内这样的考虑是相对保守的。文献[22]基于障碍函数提出了一种考虑约束的高超声速飞行器制导与控制一体化设计方法。文献[23]考虑了HFV飞行条件的变化,提出了一种考虑非对称时变迎角约束的自适应控制方法。然而,上述方法中跟踪误差的收敛速率问题没有被考虑。
据作者所知,尚未有关于考虑非对称时变迎角限制的HFV非奇异固定时间跟踪控制方法被公开报道。因此,本文为HFV设计了一种新型考虑非对称时变迎角限制的非奇异固定时间跟踪控制器,主要创新点归纳如下:
1)提出了一种跟踪误差快速收敛的迎角受限跟踪控制方法,相比于现有的HFV迎角受限文献[8]、[21-23],本文方法可以使跟踪误差在固定时间收敛至零的任意小邻域,提升了系统的稳定速度。
2)设计了一种光滑切换开关函数,避免了固定时间控制方法中的奇异值问题,并且保证了控制输入的值和导数在切换处连续。
3)提出了一种新的固定时间稳定的补偿系统,用来补偿迎角虚拟控制器饱和系统不确定性给控制性能带来的不利影响。相比于文献[21],本文方法可以将补偿信号由指数稳定提高到固定时间稳定。
1 高超声速飞行器动力学模型及预备知识
1.1 飞行器动力学模型
考虑到超燃冲压发动机对飞行姿态异常敏感和为了节省燃料,实际飞行中HFV应尽量避免横向机动,HFV的纵向动力学模型可表示为[14]:
(1)

(2)
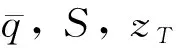
(3)
1.2 模型分解
本文采用反步法设计控制器,为了便于控制器设计,假设sinγ≈γ, cosγ≈1[16]。考虑外部扰动和气动参数摄动,将式(1)~(3)分解为速度子系统和高度子系统,分别表示为:
(4)
(5)
式中:
(6)
式中:F=[FV,Fγ,Fα,FQ]T受气动参数摄动和不可控弹性状态影响,为系统的不确定项;gV和gQ等于标称气动参数计算得到的值;d=[dV,dh,dγ,dα,dQ]T为未知的外界扰动。
假设1[24].存在未知但有界的正函数FiM,diM,i∈{V,h,γ,α,Q}使得|Fi|≤FiM, |di|≤diM。

1.3 预备知识

V(x)≤-aVp(x)-bVq(x)+η
(7)
那么称系统的轨迹是实用固定时间稳定的,并且稳定时间Ts可以估计为:
(8)
式中:0<φ<1,系统的解将收敛至如下紧集内:
(9)
引理2[27].对于任意a≥0,b>0,c>0,下列不等式成立:
(10)
引理3[27].对于任意a>0,b≤a,c>1,下列不等式成立:
(a-b)c≥bc-ac
(11)
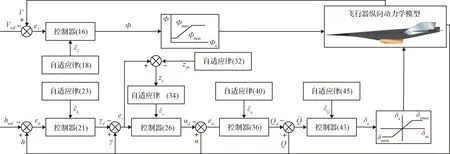
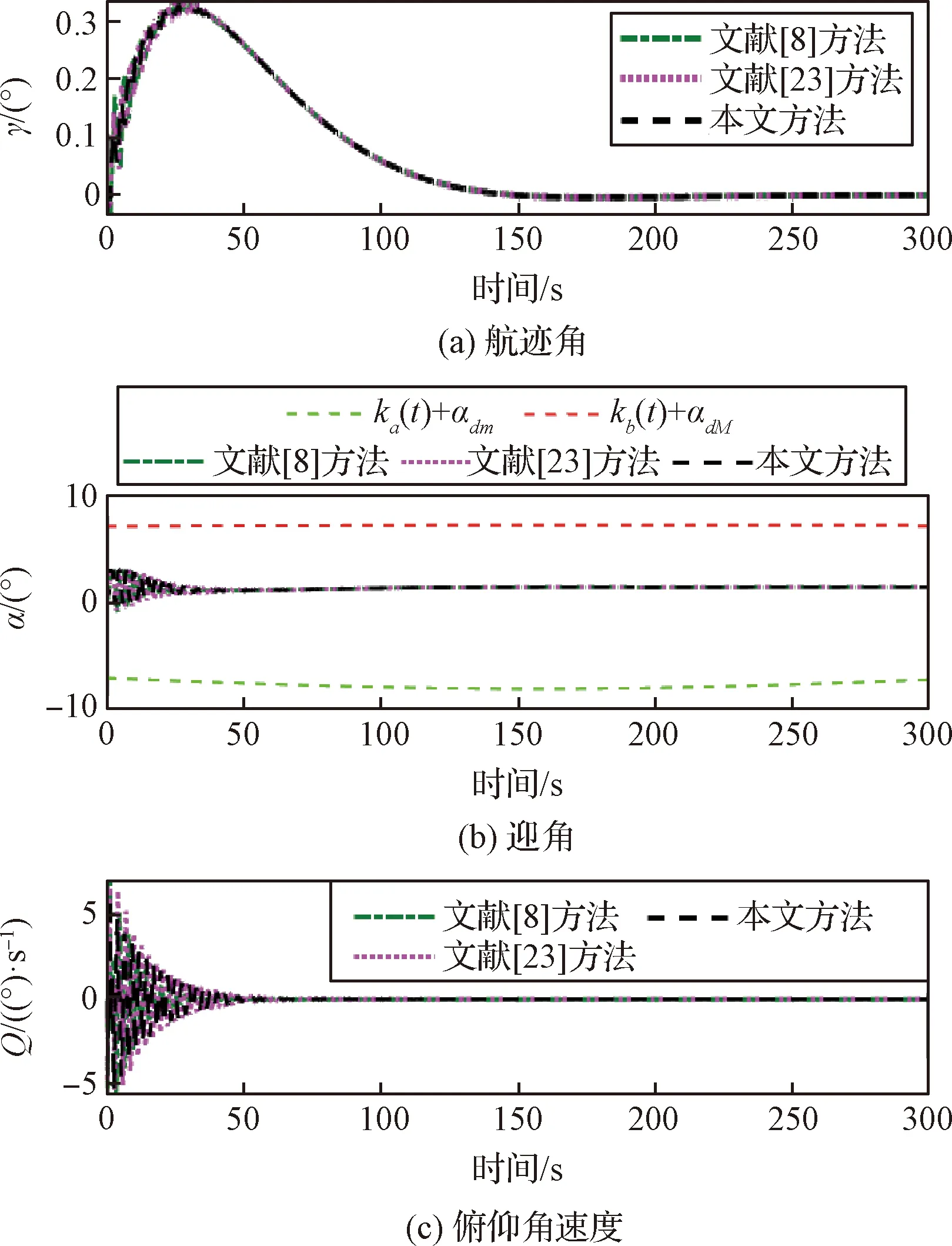
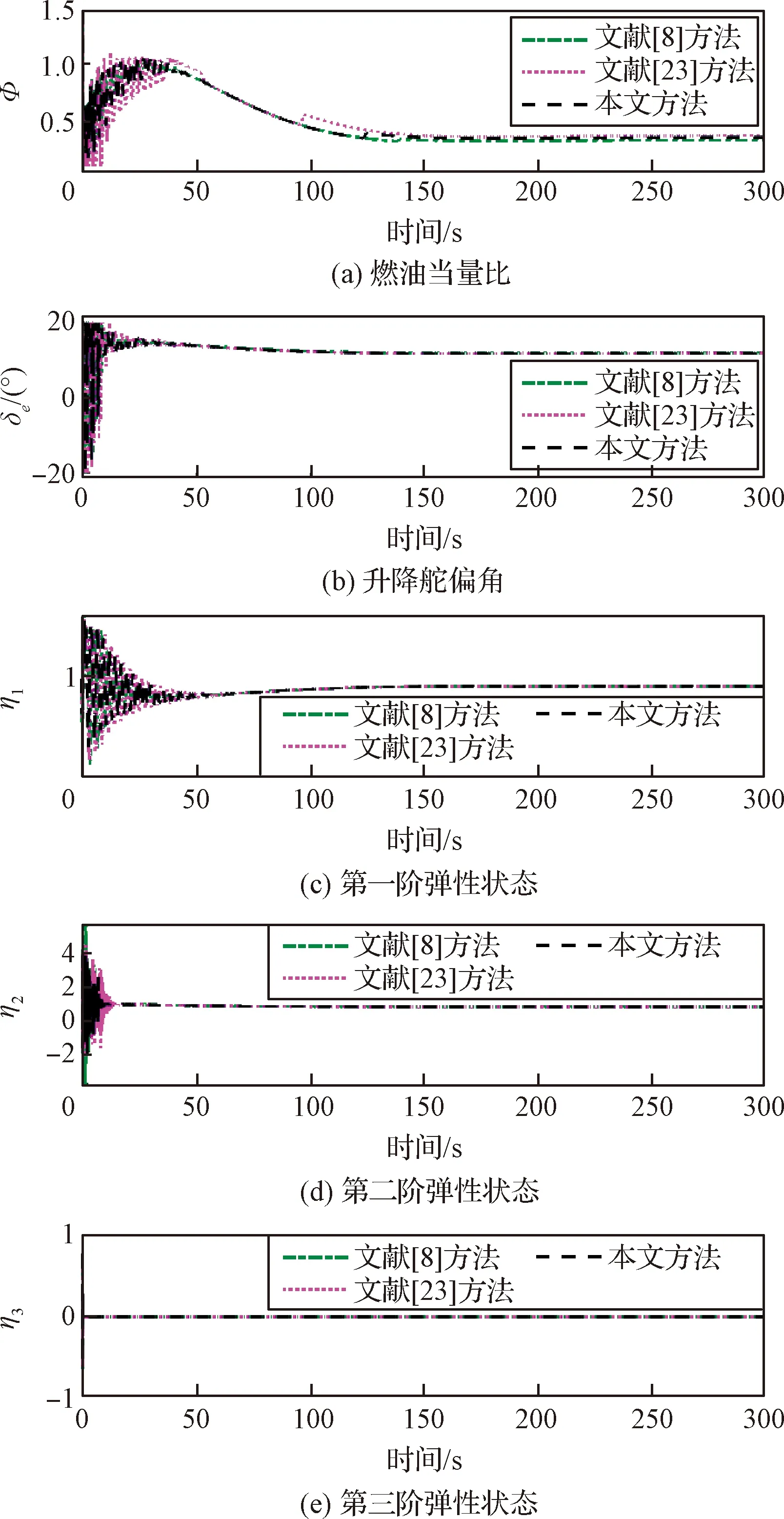
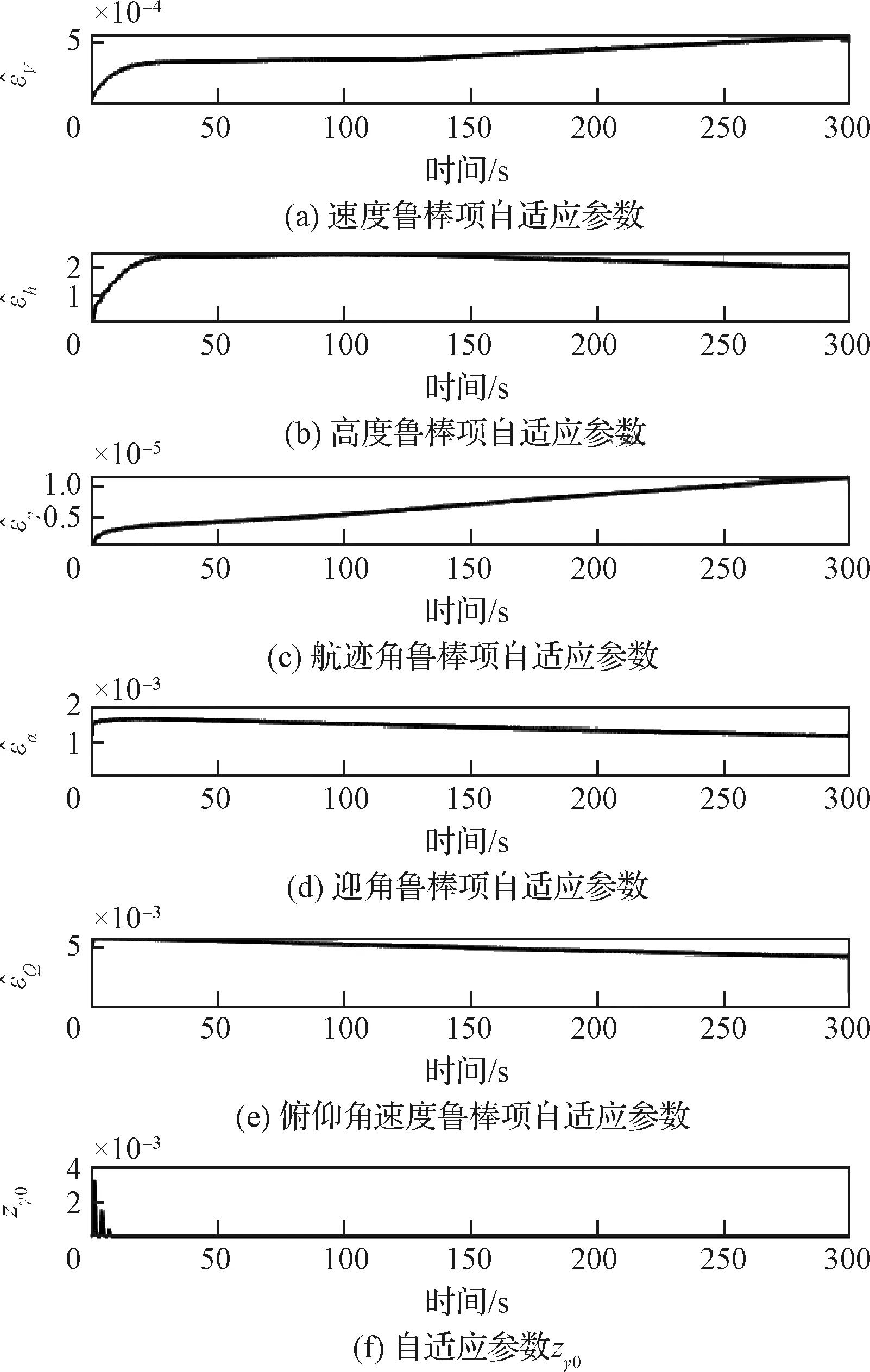
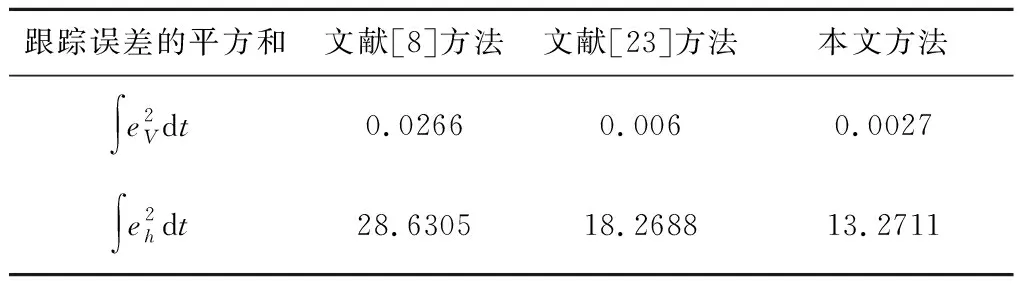
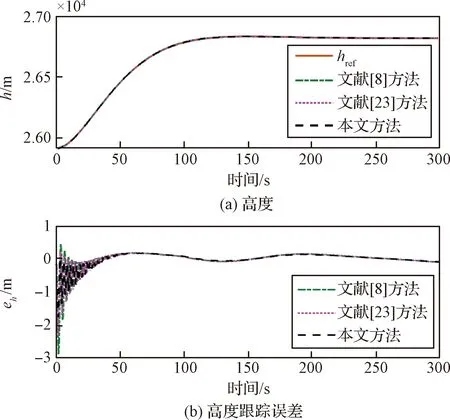
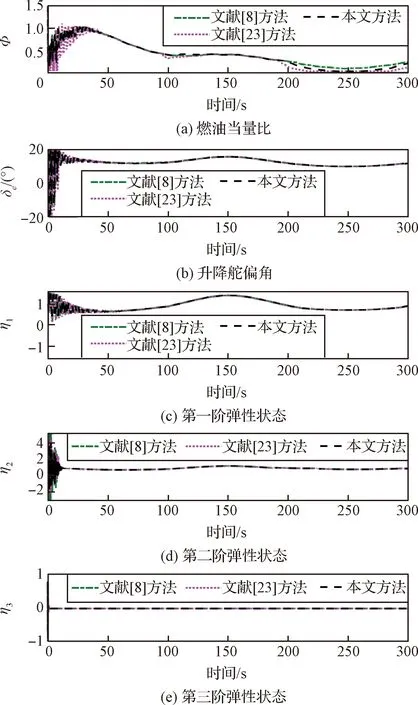
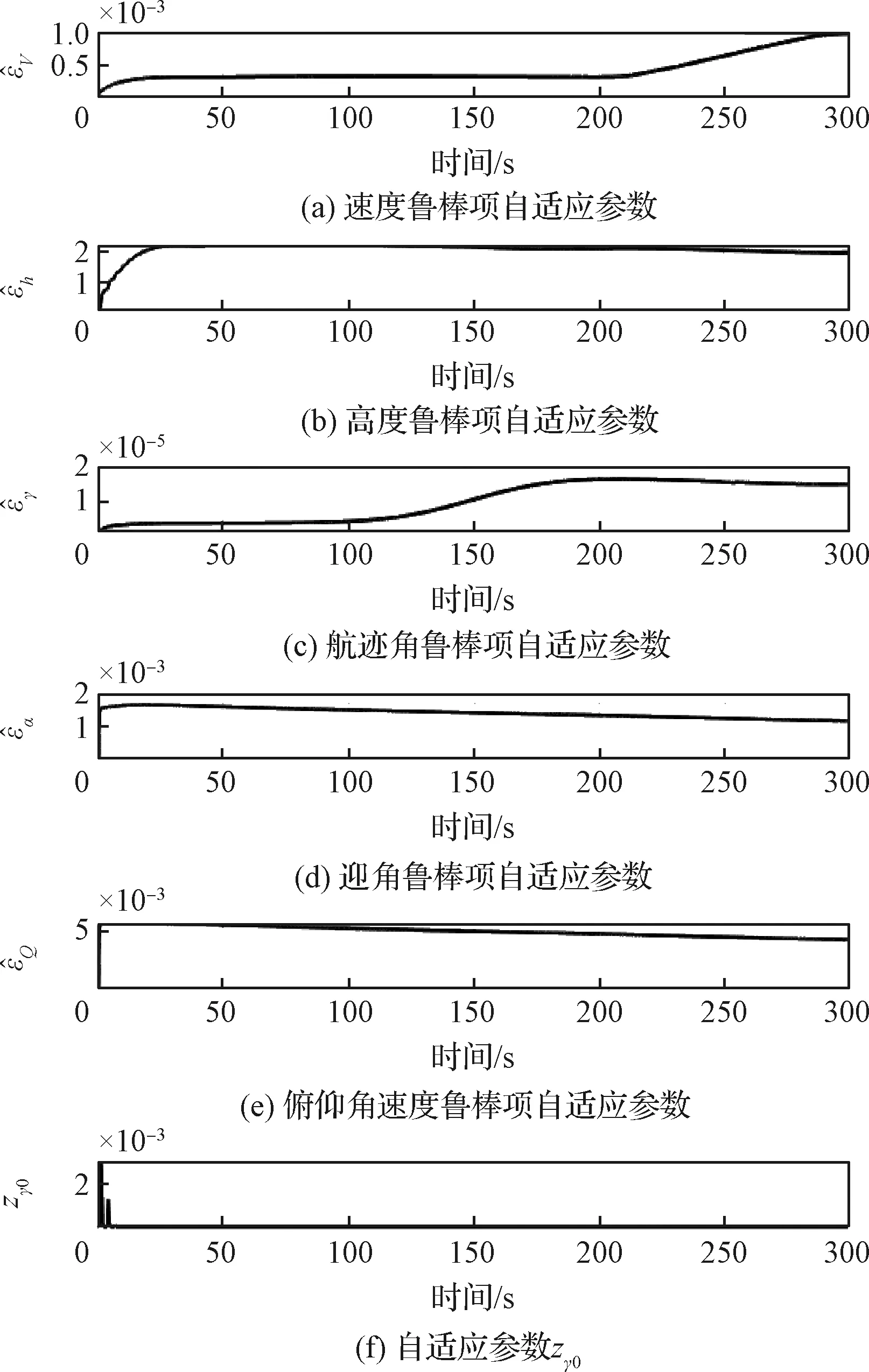
引理4[28]:对于任意k>0,如果存在常数e满足|e| (12) (13) 定义速度跟踪误差为: eV=V-Vref (14) 式中:Vref为速度参考指令。结合式(4)和式(14),eV的导数为: (15) (16) 式中:p>1,kV1,kV2,kV3,σV为正的设计参数。sg(·q)=sgn(·)|·|q, sgn(·)为符号函数。切换函数ћV被设计为: (17) 式中,0 设计自适应律为: (18) 式中:lV1,lV2,lV3为正的设计参数。 1) 定义高度跟踪误差为: eh=h-href (19) 式中:href为速度参考指令。结合式(5)和式(19),eh的导数为: (20) (21) 式中:kh1,kh2,kh3,σh为正的设计参数。切换项ћh设计为: (22) 式中:τh为正的设计参数。 设计自适应律为: (23) 式中:lh1,lh2,lh3为正的设计参数。 2) 定义航迹角跟踪误差为: eγ=γ-γd (24) 结合式(5)和式(24),eγ的导数为: (25) (26) 式中:kγ1,kγ2,kγ3,σγ为正的设计参数。切换项ћγ设计为: (27) 式中:τγ为正的设计参数。 为了满足迎角限制,令αd通过如下饱和函数: (28) 式中:αdM和αdm分别为αd的设计上下界。 定义迎角跟踪误差为: eα=α-αds (29) bα=αds-αd (30) 结合式(5)、式(29)和式(30),eγ的导数为: (31) 为了补偿虚拟控制器饱和带来的不利影响,定义zγ=eγ-zγ0。设计zγ0的自适应律为: (32) zγ的时间导数为: (33) 设计自适应律为: (34) 式中:lγ1,lγ2,lγ3为正的设计参数。 3) 由式(29)可得eα的导数为: (35) (36) 式中:kα1,kα2,kα3,σα为正的设计参数。切换项ћα设计为: (37) 式中:τα为正的设计参数。 (38) 式中:οα为正的设计参数。 非对称时变函数k(t)为: (39) 设计自适应律为: (40) 式中:lα1,lα2,lα3为正的设计参数。 4) 定义俯仰角速度跟踪误差为: eQ=Q-Qd (41) 结合式(4)和式(41),eQ的导数为: (42) (43) 式中:kQ1,kQ2,kQ3,σQ为正的设计参数。切换项ћQ设计为: (44) 式中:τQ为正的设计参数。 设计自适应律为: (45) 式中:lQ1,lQ2,lQ3为正的设计参数。 本文设计的迎角受限控制器框图如图1所示。 图1 迎角受限控制器设计框图Fig.1 The design block diagram of the controller with AOA constraint 定理 1.考虑HFV动力学系统(4)~(5),如果假设1~2成立且迎角初始跟踪误差满足ka(0) 证.选择如下Lyapunov函数: L=LV+Lh+Lγ+Lα+LQ (46) 式中: (47) (48) (49) 对式(47)求导并代入式(15),(18),(20),(23),(25),(42),(45),可得: (50) 将式(16),(21),(43)代入式(50)得: (51) 根据杨氏不等式可得: (52) (53) 根据引理2~3可得: (54) (55) 根据引理5可得: (56) 将式(52)~(56)代入式(51)中,可得: (57) 对式(48)求导并代入式(32)~(34),可得: (58) 由杨氏不等式得: (59) (60) 结合式(53)~(55)和式(59)~(60),可将式(58)推导为: (61) 对式(49)求导并代入式(35)和式(40),可得: (62) 将式(36)代入式(62)并利用引理5,可得: (63) 由式(38)可得: (64) 根据杨氏不等式可得: (65) 根据式(46),(57),(61)和(65),可得: (66) 根据式(17),(22),(27),(37),(44)中ћ·的设计,式(66)可分为以下两种情形讨论。 1) 当|e·|>τ·时,式(66)可写为: (67) 式(67)可写为如下形式: (68) 式中: 2) 当|e·|≤τ·时,式(69)可写为: (69) 式(69)可写为如下形式: (70) (71) 式中:Vref(s)和href(s)为滤波器的输入;Vc(s)和hc(s)为滤波器的输出。 表1 高超声速飞行器的初始状态Table 1 Initial states of HFV 为了说明本文所提的考虑非对称时变迎角限制固定时间跟踪控制器的有效性,将本文方法与文献[8]中的考虑对称迎角限制的跟踪控制器以及文献[23]中的考虑非对称时变迎角限制的跟踪控制器进行对比分析。 情形1:假设气动参数等于标称值,且无外界扰动,且存在初始误差eV(0)=-0.1524 m/s,eh(0)=-0.1524 m。 情形1下的速度和速度跟踪误差如图2所示,高度和高度跟踪误差如图3所示。可以看出,在标称参数情形下,采用本文方法产生的速度跟踪误差的超调量和高度跟踪误差的超调量要小于文献[8]和文献[23]方法产生的超调。图4为航迹角、迎角和俯仰角速度,采用三种方法的迎角均能保持在预设限制内。图5为迎角虚拟控制律和迎角跟踪误差,采用三种迎角受限跟踪控制方法都能将迎角虚拟控制律和跟踪误差限制在设定范围内。燃油当量比、升降舵偏角和弹性状态如图6所示,可见采用本文方法的控制输入和弹性状态很快稳定。从图7可外界以看出,本文方法的鲁棒项自适应参数及自适应参数zγ0是有界的。为了更加明显地比较三种方法的控制性能,将三种方法的速度跟踪误差的平方和以及高度跟踪误差的平方和列于表2中。可见,采用本文方法得到的速度跟踪误差平方和以及高度跟踪误差平方和都小于文献[8]和文献[23]方法得到的速度跟踪误差平方和以及高度跟踪误差平方和。因此,本文方法具有更好的控制性能。 图2 速度和速度跟踪误差Fig.2 The velocity and tracking errors of velocity 图3 高度和高度跟踪误差Fig.3 The altitude and tracking errors of altitude 图4 航迹角、迎角和俯仰角速度Fig.4 The flight path angle, AOA and pitch rate 图5 迎角虚拟控制律和迎角跟踪误差Fig.5 The virtual law of AOA and tracking errors of AOA 图6 燃油当量比、升降舵偏角和弹性状态Fig.6 The Fuel equivalent ratio, elevator deflection angle and flexible states 图7 鲁棒项自适应参数及自适应参数zγ0Fig.7 The adaptive parameters of robust term and the adaptive parameters zγ0 表2 情形1的跟踪误差平方和Table 2 The squares sum of tracking errors for Case 1 情形2:假设初始误差与情形1相同,考虑未知扰动dV=sin(0.1πt),dγ=dα=0.001sin(0.01πt),dQ=0.01sin(0.01πt),以及气动参数摄动: (72) 式中:Ci,i∈{L,D,M,T}表示考虑不确定性的参数值,Ci0表示标称的参数值。 情形2下的速度和速度跟踪误差如图8所示,高度和高度跟踪误差如图9所示。可见本文方法不仅能使速度和高度更快地跟踪上参考指令,而且在受到外界扰动影响时,能使跟踪误差的波动更小。航迹角、迎角和俯仰角速度如图10所示,采用三种控制方法皆能保证迎角不超出预设限制。图11为迎角虚拟控制律和迎角跟踪误差,采用三种控制方法都能将迎角虚拟控制律和跟踪误差限制在设定范围内。图12为燃油当量比、升降舵偏角和弹性状态。图13显示本文方法的鲁棒项自适应参数及自适应参数zγ0是有界的。情形2的速度跟踪误差的平方和以及高度跟踪误差的平方和如表3所示,在存在参数摄动和外界扰动的情形下,本文方法仍具有更加优越的控制性能。 图8 速度和速度跟踪误差Fig.8 The velocity and tracking errors of velocity 图9 高度和高度跟踪误差Fig.9 The altitude and tracking errors of altitude 图10 航迹角、迎角和俯仰角速度Fig.10 The flight path angle, AOA and pitch rate 图11 迎角虚拟控制律和迎角跟踪误差Fig.11 The virtual law of AOA and tracking errors of AOA 图12 燃油当量比、升降舵偏角和弹性状态Fig.12 The fuel equivalent ratio, elevator deflection angle and flexible states 图13 鲁棒项自适应参数及自适应参数zγ0Fig.13 The adaptive parameters of robust term and the adaptive parameters zγ0 表3 情形2的跟踪误差平方和Table 3 The squares sum of tracking errors for case 2 本文考虑非对称时变迎角限制、气动参数不确定性以及外界扰动的影响,开展了高超声速飞行器的固定时间非奇异跟踪控制研究。通过理论分析和仿真验证,有如下结论成立: 1) 设计了固定时间非奇异鲁棒跟踪控制器,保证系统的跟踪误差和估计误差在固定时间内收敛,且能避免奇异点问题。 2) 所设计的控制器能够保证高超声速飞行器的迎角始终不超出预设的非对称时变限制。 3) 相比于跟踪误差按指数收敛的迎角受限控制器,所设计控制器具有更好的控制性能。

2 固定时间自适应控制器设计
2.1 速度控制器

2.2 高度控制器
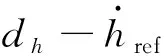
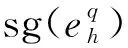

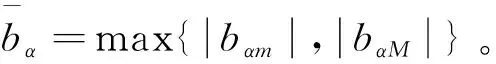
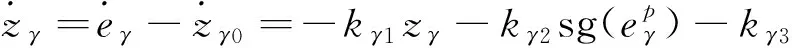

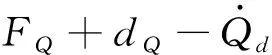
3 稳定性分析
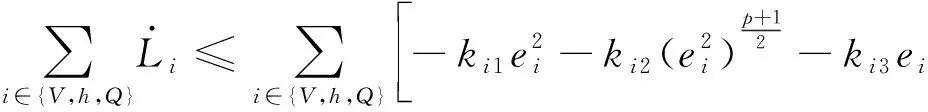
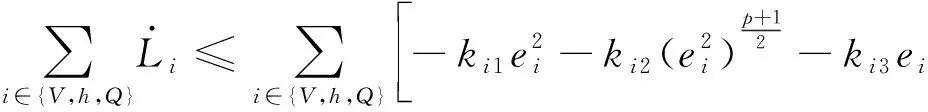
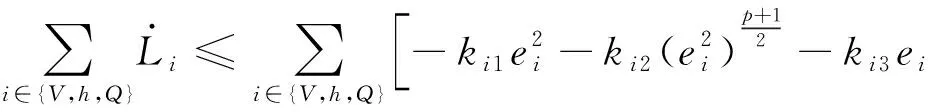

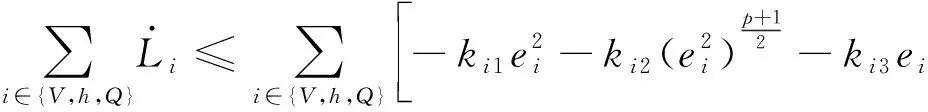
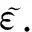
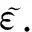
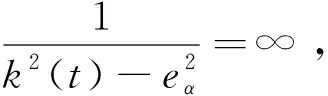
4 仿真校验









5 结 论
