面向木星卫星交会任务的探测器飞行路径规划

田百义，张 熇，冯 昊，张相宇，高博宇，周文艳

(北京空间飞行器总体设计部，北京 100094)

0 引 言

木星是太阳系从内向外的第五颗行星，是太阳系中体积最大、自转最快的行星。木星也是迄今为止具有最多卫星的行星，已发现66颗天然卫星，俨然是一个小型的太阳系，因此常被称为木星系统。1610年，伽利略最早用望远镜发现木星最亮的4颗卫星，被后人称为伽利略卫星，这四颗卫星环绕在离木星400000～1900000 km的轨道带上，由内而外依次为木卫一(Io)、木卫二(Europa)、木卫三(Ganymede)和木卫四(Callisto)[1]。

木星系统是国际上探测的热点目标之一，通过对木星及其卫星的近距离探测对于了解气态巨行星的起源和演化，以及太阳系的发展具有重要意义。迄今为止，欧美国家针对木星系共进行了9次探测，其中1989年发射的伽利略号[2-3]和2011年发射的朱诺号[4]，均已实现了对木星的环绕探测。欧空局计划于2023年发射的JUICE探测器[5-6]将重点针对木卫三进行环绕探测，美国计划于2024年发射的欧罗巴-快船(Europa Clipper)探测器[7-8]将重点对木卫二进行高达44次的飞越探测。根据《2021中国的航天》白皮书规划，未来五年，中国继续实施行星探测工程，计划完成火星采样返回、木星系探测等关键技术攻关。

在深空探测任务中，借力飞行是一项被广泛应用的技术，它不但可以降低探测器发射所需的能量，而且还能有效降低探测器的速度增量需求，从而节约大量的推进剂。国际上很多已发射的探测器都采用了借力飞行技术，如先驱者10/11号[9]、旅行者1/2号[10]、新视野号[11]、卡西尼号[12]、露西号[13]等，以及如前所述的木星探测器伽利略号、朱诺号等等。除上述任务之外，学者也对采用借力飞行的多种深空探测任务轨道进行了设计。文献[14]对地球至木星的借力飞行轨道进行了设计；文献[15]对采用行星借力进行太阳系逃逸和柯伊伯带小天体探测飞行轨道进行了设计；文献[16]在给定飞行时间约束下，对2029～2037年发射探测器探测位于海王星轨道之外的天体Sedna的借力飞行轨道进行了优化设计；文献[17]对采用行星借力的太阳系边际探测任务轨道进行了规划和设计。目前，借力飞行技术已发展成熟，对应也发展出了多种借力轨道设计的方法。文献[18]提出了基于C3匹配的遍历式搜索设计方法，并开发了STOUR的相关模块；文献[19]将借力飞行轨道设计问题归结为一个全局优化问题，采用基于系统分支策略的进化算法求解该问题；文献[20]将行星借力视为一个连续过程，提出了一种采用伪状态理论的借力飞行轨道初始设计方法；文献[21]给出了一种基于伪状态理论和深度神经网络的精确多重借力飞行轨道设计的混合方法。

在木星系探测的轨道研究方面，文献[2]对1986年发射伽利略任务的环木轨道方案进行了介绍；文献[3]对伽利略任务的飞行轨道情况进行了介绍；文献[7-8]详细介绍了Europa Clipper任务中环木飞行轨道，并给出了面向木卫二多次飞越任务的转移轨道设计方法；文献[22-23]研究了一种面向木星探测和木卫着陆任务的借力飞行轨道设计方法；文献[4]在朱诺号任务介绍中，也给出了朱诺号探测器的星际转移轨道和木星极轨探测飞行的轨道方案。在国内，文献[24]针对木星系多目标探测任务，提出了三种候选轨道设计方案，以实现对木星极区、木星表面精细结构以及木星伽利略卫星的探测；文献[25]系统性的梳理了环木星探测器的受力问题，详尽的整理了相关的计算公式及具体参数，给出了绕飞阶段轨道计算需要考虑的时空参考系、动力学模型。上述研究均停留在木星环绕探测的飞行轨道方案设计或模型研究层面，并未给出木星系内飞行的路径规划的方法。

本文给出了一种探测器在木星系内环绕探测飞行的路径规划方法，该方法可根据任务约束自动搜索探测器在木星系统内的借力序列。该方法采用三层的优化策略，第一层(底层)采用全局优化算法，对给定借力序列的两次借力飞行轨道进行优化；第二层采用遍历的方法，对所有潜在的飞行序列轨道进行遍历；第三层采用贪婪算法的思想，选取其中速度增量最优的一个局部序列作为探测器飞行路径的一部分。该方法无需提前指定探测器的飞行路径，自动实现探测器在木星系内飞行的路径规划和轨道优化设计，可为我国木星系探测任务提供技术基础。

1 轨道动力学模型

1.1 运动模型

文章采用探测器在木心惯性坐标系下的二体运动方程，形式如下：

(1)

式中：r,v为飞行器的位置速度矢量；μ为中心天体(木星)引力系数。

1.2 木卫借力模型

当探测器在木星引力场中近距离飞越木卫时，木卫的引力将改变探测器环木飞行的轨道。木卫借力的轨道相对木卫而言，是一条以木卫质心为焦点的双曲线轨道，探测器在木卫影响球边界处相对木卫的速度为双曲线剩余速度V∞。在探测器自由飞行状态下，木卫借力前后的V∞大小相等，即

(3)

式中：μJ_M为借力天体-木卫的引力常数。

本文采用基于B平面参数的借力模型[26]，该模型以B平面角b和近心点距rp为参数。取探测器飞入木卫的双曲线剩余速度矢量为V∞in=[vx∞-,vy∞-,vz∞-]T，则由B平面参数的几何关系，可以得到探测器的飞出双曲线剩余速度的矢量V∞out。

(4)

式中：

(5)

根据上述原理，若已知探测器相对木卫的飞入双曲线剩余速度矢量、借力轨道近心点距rp和B平面角b，则可以得到探测器在飞越木卫之后的双曲线剩余速度矢量。

2 借力轨道优化模型

借力飞行轨道优化设计的核心是确定探测器每次木卫飞越时的历元、高度和方位等参数，从而使得任务目标(速度增量需求)达到最优或次优。而这一问题恰好可以转化为含有多个非线性约束的多参数优化问题，之后再利用优化算法进行求解，从而解决该问题。

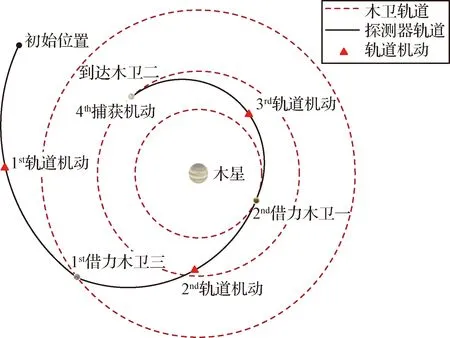
图1 探测器经两次木卫借力到达木卫二的飞行轨道示意图Fig.1 The probe’s trajectory after two times of gravity assists by the Jupiter’s moon to the Europa

以木卫二交会任务为例，探测器由初始位置经木卫三和木卫一两次木卫借力，以及三次轨道机动后，实现与木卫二的交会，图1给出了探测器飞行轨道设计模型示意图。

已知探测器初始时刻的位置和速度矢量，则轨道优化设计的目标是获取探测器每次机动时刻、大小和方向，以及每次木卫借力的时刻、高度和方位等参数，使得探测器到达木卫二时，探测器总的速度增量(轨道机动和木卫二捕获机动)需求达到最优。

轨道设计时，不妨取如下假设：借力前后，木卫的位置不变，探测器借力时的位置与木卫位置重合。因此，轨道优化模型中的待优化变量应至少包括如下10个：

1)两次木卫借力时刻TGA及到达木卫时刻TA，3个变量。用于确定各飞行阶段的初始位置和速度；

2)三次轨道机动时刻TDV，3个变量。用于各个飞行段轨道参数的拼接；

3)两次木卫借力参数：借力近心距rp和B平面角b，4个变量。用于木卫借力前后轨道参数的拼接。

给定上述参数之后，根据Spice星历模型，可获取各次木卫借力时刻木卫的位置和速度矢量。由探测器初始历元时刻的位置和速度矢量，向后进行开普勒轨道递推，可得到探测器第一次轨道机动时刻的位置和速度矢量；根据第一次轨道机动时刻的位置和木卫一借力时刻的位置，及轨道机动至木卫三借力的飞行时间，求解兰伯特问题，得到探测器在轨道机动后和木卫三借力前的速度矢量，轨道机动前后的速度矢量差，即为第一次轨道机动的速度增量矢量，木卫三借力前的速度矢量与木卫三的速度矢量差，即为木卫三借力的飞入双曲线剩余速度。依次类推，可得到探测器后续各次轨道机动及木卫二捕获机动的速度增量矢量。从而建立由待优化参数表征的优化目标，将借力飞行轨道优化问题转化为多维参数优化的问题,待优化参数：

Z=[TGA1,TGA2,TA,TDV1,TDV2,TDV3,rp1,rp2,b1,b2]T

优化指标：J=ΔV→min

上述优化模型可采用粒子群或遗传等全局优化算法进行求解，从而完成探测器飞行轨道的优化设计。本文采用MATLAB优化工具箱中的遗传算法进行优化，设置人口100，计算代数为500，其余参数如变异因子等，按程序默认设置即可。

3 基于贪婪思想的飞行路径规划方法

贪婪算法是从某一起点开始，在每一个解决问题的步骤使用贪心原则，都采取在当前状态下最有利或最优化的选择，不断地改进该解答，持续在每一个步骤中选择最佳的方法，并且逐步逼近给定的目标，当达到某一个步骤不能再继续前进时，算法中止。

以实现木卫二交会为例，基于贪婪思想的飞行路径规划过程如图2和图3所示。该方法需要开展如下三层的优化：

1) 根据探测器的初始位置和速度，对给定的交会目标和任意给定2个飞越目标进行探测器的速度增量优化，优化模型见第2节。

3) 采用贪婪的思想，每一步均选择速度增量最优的飞行路径。

在每一次完成上述三层优化时，均需要计算探测器的总的飞行时间，探测器总飞行时间超出任务约束，则计算停止。否则，取飞越目标2之后的位置和速度为后续优化的初始位置和初始速度，进入下一步的贪婪路径规划。

图2 面向木卫交会任务的多目标探测路径规划流程Fig.2 Flight path planning process for the rendezvous mission of the Jupiter’s moon

图3 基于贪婪思想的飞行路径规划过程示意图Fig.3 Flight path planning process based on greedy algorithm

图3给出了探测器飞行路径规划过程示意图。其中，第1次贪婪计算中需要优化的飞行序列包括“初始位置-木卫一-木卫一-木卫二”、“初始位置-木卫一-木卫二-木卫二”、“初始位置-木卫一-木卫三-木卫二”、“初始位置-木卫一-木卫四-木卫二”、“初始位置-木卫二-木卫一-木卫二”、“初始位置-木卫二-木卫二-木卫二”、“初始位置-木卫二-木卫三-木卫二”、“初始位置-木卫二-木卫四-木卫二”、……、“初始位置-木卫四-木卫四-木卫二”，共16个飞行序列。采用贪婪算法的思想，取出其中速度增量最优的一个序列“初始位置-木卫三-木卫一-木卫二”为第1次贪婪计算的结果，确定木卫三和木卫一为第1次贪婪计算所得到的飞越目标。然后，将木卫一借力之后的状态(包括历元时刻、位置和速度)作为第2次贪婪计算的初始位置，再次对上述16个飞行序列进行优化，完成优化会后，仍然采用贪婪算法的思想，取出其中速度增量最优的序列“初始位置-木卫二-木卫四-木卫二”，为第2次贪婪计算的结果，确定木卫二和木卫四为第2次贪婪计算所得到的飞越目标。然后，将木卫四借力之后的状态(包括历元时刻、位置和速度)作为第3次贪婪计算的初始位置。最终经过Nc次贪婪计算，确定探测器的飞行路径为“初始位置-木卫三-木卫一-木卫二-木卫四-……-木卫二-木卫二-木卫二”，从而完成面向木卫二交会任务的飞行路径规划。

在完成每一次的贪婪计算后，计算探测器总的飞行时间和总的贪婪计算次数，当飞行时间超出任务时间约束或贪婪计算次数k达到预先设定的值Nc后，则结束贪婪计算，并完成飞行任务规划，如图2所示。

4 仿真分析

不妨取探测器被木星捕获后的初始轨道参数如下：

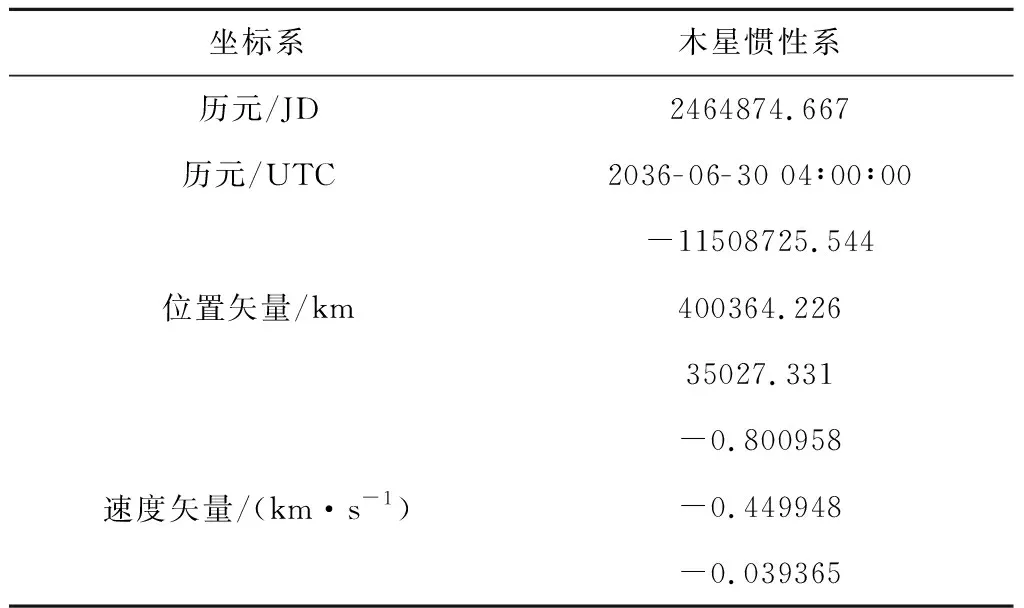
表1 探测器初始轨道参数Table 1 Initial orbit parameters of the probe

约束探测器环木飞行时间不大于10年，贪婪次数不大于100次，木卫借力高度不小于100 km，分别选择交会目标为木卫一、木卫二、木卫三或木卫四进行仿真分析，探测器环绕木卫轨道为200 km的圆轨道。

以木卫二环绕探测任务为例，采用本文的规划方法，得到探测器飞行路径和环木飞行轨道如表2和图5(b)所示，图中1LU等于1倍的木星半径，为71492 km。木卫二交会任务的贪婪计算次数为100次，共进行200次的木卫飞越，总的飞行时间8.426年，速度增量(深空机动和木卫二捕获机动)需求随借力次数变化关系见图4(b)。由此可知：

1)随着贪婪次数的增加，探测器速度增量需求显著减小，在借力次数为32(贪婪次数为16)时，探测器总的速度增量需求达到最优，随着借力次数的进一步增加，探测器飞行路径收敛于木卫二，总的速度增量需求逐步增大。因此，确定木卫借力32次的飞行路径为探测器的飞行轨道，其中木卫一飞越11次，木卫二飞越12次，木卫三飞越6次，木卫四飞越3次。探测器环木飞行时间为2.965年，总的速度增量需求为2.8591 km·s-1，其中木卫二捕获制动速度增量需求1.6636 km·s-1，深空机动速度增量需求1.1955 km·s-1。

图4 木卫交会任务速度增量需求随借力次数的改变情况Fig.4 Change of the speed increment demand of the rendezvous mission with the times of flyby

表2 木卫一至木卫四交会任务的飞行路径规划结果Table 2 The results of flight path planning for Jupiter’s moons

续表2

2)若选择对木卫二180次的飞越代替对木卫二的环绕探测，则探测器总的速度增量需求可降低为1.8957 km·s-1。

对于木卫一、木卫三和木卫四的交会任务轨道，其速度增量和飞行路径的规律与木卫二交会任务相类似，此处不再赘述。从实现交会任务的速度增量角度考虑，木卫四交会任务的速度增量需求最小，为2.2805 km·s-1，其后依次为木卫三(2.3743 km·s-1)、木卫二(2.8591 km·s-1)和木卫一(3.7537 km·s-1)。

图5 面向不同木卫交会任务的探测器飞行轨道示意图Fig.5 The probe’s flight path for the rendezvous mission of the different Jupiter’s moons

以木卫四交会任务为例进行进一步分析。

1)贪婪计算1次，得到探测器飞行序列为：“初始状态-木卫四-木卫二-木卫四”，总速度增量2.8790 km·s-1，其中木卫四捕获速度增量需求2 km·s-1，中途三次轨道机动的速度增量需求为0.8790 km·s-1；

2)贪婪计算2次，探测器飞行序列增加两个，为：“初始状态-木卫四-木卫二-木卫二-木卫三-木卫四”，总速度增量减小为2.8286 km·s-1；

3)贪婪计算3次，探测器飞行序列又增加两个，为：“初始状态-木卫四-木卫二-木卫二-木卫三-木卫三-木卫四-木卫四”，总速度增量减小为2.6433 km·s-1；

4)以此贪婪计算下去，直到贪婪计算5次，总的速度增量减小至最优/次优值2.2805 km·s-1。对应的最优/次优飞行序列为“初始状态-木卫四-木卫二-木卫二-木卫三-木卫三-木卫四-木卫四-木卫四-木卫四-木卫四-木卫四”。因此，通过多次的木卫借力飞行，可以显著降低探测器的速度增量需求。

表3给出了探测器速度增量最优/次优的飞行轨道方案。探测器由初始时刻，经10次借力和11次轨道机动，共消耗速度增量2.2805 km·s-1，总飞行时间3.0135年，即可进入环绕木卫四平均高度200 km的目标圆轨道。

表3 木卫四交会任务的飞行轨道方案Table 3 The flight orbit scheme forthe Ganymede rendezvous mission

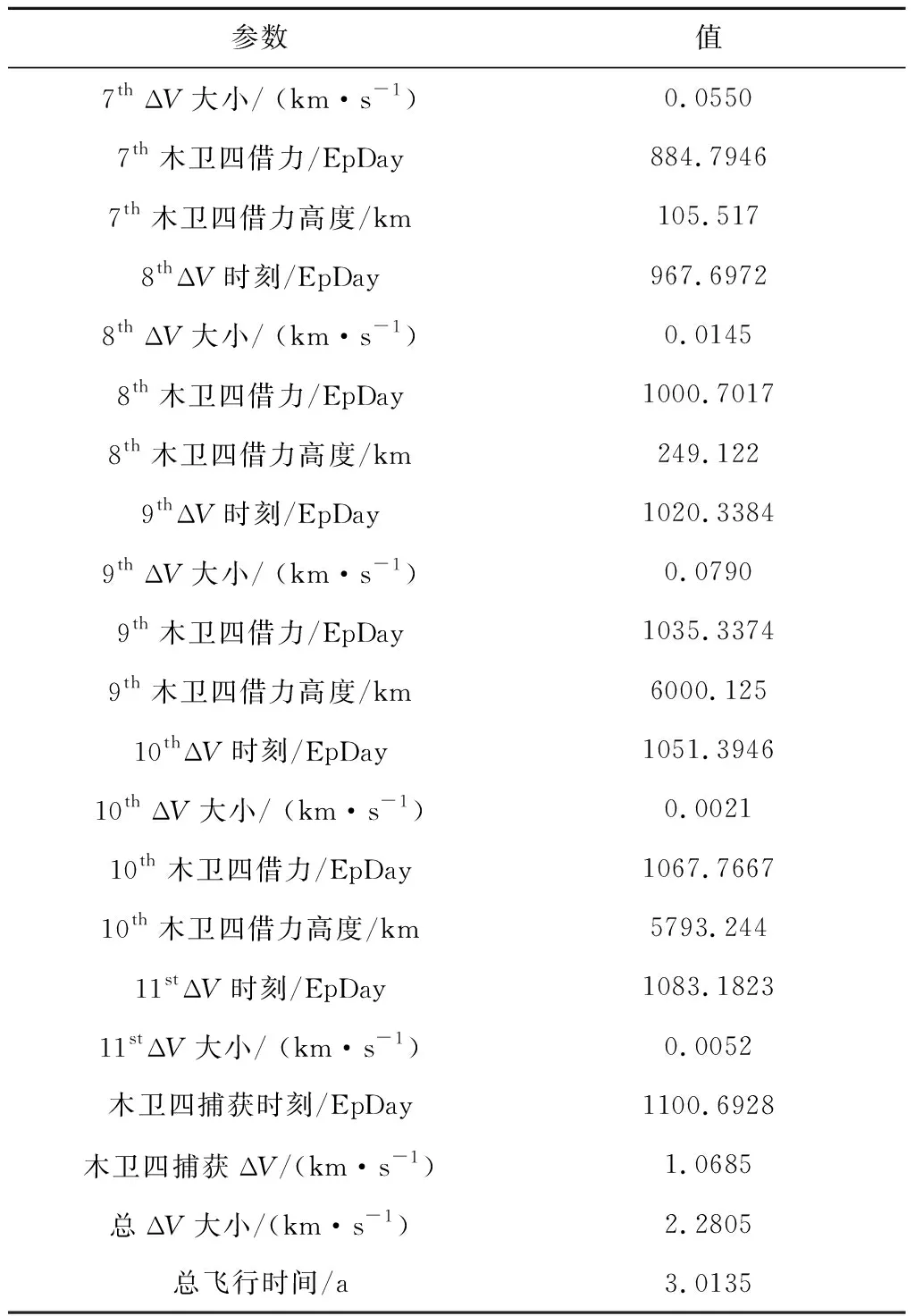
续表3

探测器的环木飞行轨道周期随贪婪计算次数的变化如图6所示。由图可知，随着贪婪计算次数的增加，探测器的环木飞行轨道逐渐向与木卫四共振比约为1∶1的共振轨道收敛。其中3次贪婪计算后，与木卫四的共振比例约为1∶4；4次贪婪计算后，与木卫四的共振比例约为1∶2；7次贪婪计算后，与木卫四的共振比例约为1∶1。

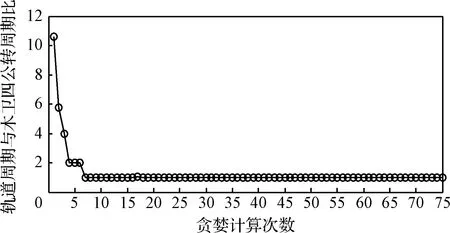
图6 探测器环木飞行轨道周期随贪婪计算次数的变化情况Fig.6 Change of the orbital period of the Ganymede rendezvous mission with the times of flyby

图7给出了贪婪计算1～6次对应的探测器环木飞行轨道情况，其中贪婪计算5次为规划所得到的最佳飞行路径。

图7 探测器环木飞行轨道随贪婪计算次数的变化情况Fig.7 Change of the transfer orbit of the Ganymede rendezvous mission with the times of flyby

5 结 论

文章针对探测器被木星捕获之后的飞行路径规划问题，采用三层优化的思路，给出了一种探测器在木星系内环绕探测飞行的路径规划方法，该方法无需提前指定探测器的飞行路径，可根据任务约束自动搜索探测器在木星系统内的飞行序列。木卫交会任务的仿真分析表明：采用本文的路径规划方法，经过多次路径贪婪选择之后，木卫交会任务对应的速度增量需求显著降低，且随着借力次数的进一步增加，探测器飞行路径收敛于交会的目标，说明本文的方法可有效逼近并获取木卫交会任务的最优飞行路径。

文章所提供的方法可对木星的任意伽利略卫星环绕探测任务进行木卫借力路径的规划和飞行轨道的优化设计。但是，该方法的待优化参数并未引入木星捕获轨道参数，而木星捕获轨道作为环木飞行轨道的初始参数，对探测器的飞行路径和速度增量需求存在较大的影响。后续的环木飞行路径规划研究时，可在第一步贪婪运算中引入木星捕获轨道参数作为待优化变量，以实现探测器木星探测任务的整体最优化设计。