一种多目标变邻域模拟退火算法及成像星座任务规划方法

丁祎男，刘羽白，王淑一，雷拥军

(1. 北京控制工程研究所，北京 100094； 2. 空间智能控制技术重点实验室，北京 100094)

0 引 言

随着对地观测任务逐渐复杂，任务需求量不断增加，各国竞相发展敏捷成像卫星组成的星座，如美国的WorldView系列卫星，法国的Pleiades星座以及我国发射的“高景”系列卫星等[1]。

敏捷成像卫星可以沿三轴机动，有很强的对地观测能力，成像星座可以进一步满足大规模的观测任务需求。相比于传统成像卫星，敏捷卫星星座成像任务规划问题的解空间更大[2]，因此选取能快速全面遍历问题所有解的优化变量尤为重要。敏捷卫星拓宽了观测时间窗口，但往往时间窗口边缘的成像质量变差，难以满足用户需求，因此提高任务完成度的同时要兼顾成像质量，这是一个工程实践中亟待解决的多约束多目标的优化问题，对模型构建和求解算法提出了更高的要求。

近年来国内外学者在卫星任务规划方面进行了大量的研究。Chen等[3]和Xiao等[4]将任务规划问题描述为混合整数线性规划模型(MILP)，采用线性规划求解器求解，可以得到稳定有效的优化结果。但MILP模型必须将约束和优化目标线性化，且优化中无法实时更新卫星和观测目标以及地面站的相对位置信息，也无法记录卫星的位置、速度、姿态信息，导致卫星在目标、地面站间的机动时间是预估的且不准确的，若任务密集则优化结果与实际情况差别较大。She等[5]针对此问题，在优化过程中周期性地更新约束条件，并用遗传算法验证求解结果，证明这是一种切实可行的方法。MILP的求解速度依赖于求解器的性能，面对大规模的观测任务规划问题，将会付出难以接受的时间代价。当前更多的研究将任务规划问题描述为一般的约束满足模型，采用元启发式搜索算法求解，如遗传算法[1-2,6-10]，模拟退火算法[11]、差分进化算法[12]，邻域搜索算法[13-14]等。这些优化算法的思想已经非常成熟，因此如何针对存在的工程实践问题设计约束条件和优化目标，以及如何构造模型和优化算法的联系以提高求解效率，是近年来研究的核心。

优化对象是问题模型和求解算法间的桥梁，找到模型中能快速、全面遍历问题所有解的变量是提高优化效果的关键。文献[6,11]采用二进制编码，以任务是否被选择观测为优化对象，该编码方式搜索效率高，但不能主动调整任务的执行顺序，搜索范围有限。文献[7-10,12-14]采用的是整数或实数编码，可以优化任务观测顺序，但成像时刻需要先初始化为在时间窗口开始或中间的位置，然后在观测顺序确定的前提下根据星上资源或机动时间的约束进行调整。文献[1]采用实数编码，以相对成像时刻作为优化对象，文献[2]采用二进制、整数、实数三种编码，同时以任务选择、任务顺序和成像时刻为优化对象，可以充分遍历解空间，发挥敏捷卫星的优势。

单以最大化任务完成度为优化目标的任务规划方法已经难以满足日益复杂的观测任务需求，但多目标优化问题比单目标优化问题的求解更为复杂。文献[1,7,12-13]考虑了最大化完成任务总权重外的其它目标，如提高成像质量、最小化能源消耗等，但都是将多目标优化问题转化为单目标优化问题，如将多个目标函数以加权的方式整合为单目标函数，或者将某几个目标以约束的方式给出。单目标优化问题求解的计算量较小，可以在较短时间内得到较好的优化结果，但这样得到的最优解是一个依赖加权系数或约束条件的平衡多个目标函数的解。这样一来难以权衡新增的参数，二来若用户需求发生变化，就需要调整参数重新规划，耗费时间。文献[9,14]采用的是Pareto多目标优化模型，分别采用多目标遗传算法和局部搜索算法求解，得到的结果是问题的最优解集，使得优化过程中每一个目标函数的最优值都得以保留。

在工程实践中，成像质量逐渐成为用户最重要的需求，而成像质量与卫星的成像时刻直接相关。文献[13]考虑了成像质量，但将其作为约束条件给出，调整成像时刻的范围不够灵活，若用户需求改变，就要修改约束重新规划。文献[12]提出了一种成像质量评价指标，并将提高成像质量与其它优化目标加权为单目标函数，取得了很好的优化效果，但其优化效果依赖于加权算法，且采用的是整数编码，不能主动调整成像时刻。

多目标模拟退火算法可以有效地求解基于Pareto模型的多目标优化问题，其邻域搜索的特性也可以很好地用于对成像时刻的优化。

综合以上分析，本文首先考虑卫星的观测时间窗口、姿态机动时间、星上资源等约束，以最大化完成任务总权重和满足用户成像质量要求为目标，建立多星多观测目标的敏捷成像卫星任务规划模型。进一步以成像时刻为优化对象，提出一种利用降温过程调节搜索范围的多目标变邻域模拟退火算法，实现对任务成像时刻的滑动优化，得到问题的最优解集，兼顾最大化完成任务总权重和满足用户成像质量要求。最后通过工程实例仿真，比较了多种优化算法的仿真结果，验证了模型构建的有效性和本文算法的优势。

1 敏捷成像星座任务规划模型

1.1 参数和变量定义

1)模型参数

P观测目标集合，P={p1,p2,…,pNP}，其中NP为观测目标数量。

S成像卫星集合，S={s1,s2,…,sNS}，其中NS为成像卫星数量。

M时间窗口(任务)集合，M={m1,m2,…,mN}，其中N为时间窗口数量。

ok目标pk的观测时长。

ωk目标pk的权重。

ai任务mi的最早成像时刻。

bi任务mi的最晚成像时刻。

ui任务mi的权重。

2)模型变量

yi卫星执行任务mi时的成像时刻。

zi任务mi的执行情况，0表示不执行任务mi，1表示执行任务mi。

qjk卫星与目标的观测关系，0表示目标pk未由卫星sj观测，1表示目标pk由卫星sj观测。

3)任务的表示

任务mi可以表示为：

(1)

1.2 多目标约束满足模型

本文构建多目标约束满足模型来描述敏捷成像卫星任务规划问题，模型主要由约束条件、决策变量以及目标函数构成。

1)约束条件

本文主要考虑了时间窗口、姿态机动时间、星上资源、任务需求等4个方面的约束条件。

(1)卫星对目标的可见性约束

若任务mi确定被执行，则必须满足

ai≤yi≤bi

(2)

(2)卫星姿态机动能力约束

卫星执行相邻任务时受机动能力的约束，若卫星sj需要先后执行任务mi′和mi，设卫星在时刻ei′执行完任务mi′，接下来要在yi时刻执行任务mi，卫星所需的机动时间为di′i，需要满足

yi-ei′≥di′i

(3)

(3)卫星星上资源约束

本文将星上能源、固存等约束都归为星上资源约束。执行任务mi消耗的资源分为两部分，一部分与卫星机动角度θi成正比，另一部分与成像时长ok成正比，比例系数分别为η1和η2，设卫星sj在执行任务mi之前的可用资源为Ej，若要执行任务mi需要满足

Ej≥η1θi+η2ok

(4)

(4)观测任务的唯一性约束

每个目标最多被观测一次，且最多只被一颗卫星观测，对于目标pk有

(5)

此约束条件可以协调卫星之间的观测行为，与约束(3)结合可以防止出现某些卫星承担了过多的观测任务而其它卫星闲置的情况，发挥成像星座的观测优势。

在实际的观测任务中，还存在卫星数传窗口、数传时机、太阳能帆板供电等因素，但这些约束在形式上都可以归到以上四种约束中，本文不再赘述。

2)决策变量

本文选取任务mi中的成像时刻yi作为决策变量，其可以唯一确定卫星执行该任务时的观测起止时间和机动轨迹，通过设定任务间的冲突处理原则，进一步可以确定整个任务序列中哪些任务可以执行和执行顺序，间接确定变量zi和qjk的值，得到可执行任务序列。因此yi可以以一个变量遍历问题的整个解空间，在搜索范围和效率方面都有一定的优势。

3)目标函数

在以往研究中，多以最大化完成任务总权重作为优化的目标，但成像质量也是成像任务执行好坏的重要评价指标，本文将提高成像质量也作为优化目标。

(1)最大化完成任务总权重

(6)

ui一般情况下与任务包含的目标pk的权重ωk相同，即ui=ωk，但若完成的任务为红外相机在阳照区成像，令ui=μωk，其中μ∈(0,1)为惩罚系数，引导优化算法优先考虑在阳照区采用可见光成像。

(2)成像质量最优化

在同一个时间窗口中，成像时刻越靠近中心，由目标到卫星的仰角越大，成像质量越高[15]，因此在优化过程中应尽可能将观测窗口移向时间窗口中心，尤其是权重高的目标，构造目标函数

(7)

为方便优化算法的求解，将目标函数式(7)转化为最大化问题

(8)

式中：α为一个正数。

这两个目标函数是有冲突的，由于时间窗口有重叠，目标函数式(8)会使任务开始执行时间尽可能安排在时间窗口中心，这样会使部分任务因时间冲突无法被观测。传统的单目标优化算法将两个目标函数加权为一个目标函数，通过调整加权系数来引导优化过程侧重优化其中一个目标，加权系数会对优化效果产生较大的影响，选择不当会丢失一些较优解。本文采用基于Pareto模型的多目标优化算法，引入非受支配解和非受支配解集的概念[16]：

设多目标优化问题包含L个目标函数、H个决策变量，其优化目标为

maxg(x)=[g1(x),g2(x),…,gL(x)]

(9)

式中：x为H维决策向量，称为问题的解；g(x)定义了L个由解空间向目标空间的映射函数。若有

(10)

则称解x1支配解x2或解x2受解x1支配，记作x1≻x2。若一个解不受问题的解集中任一解支配，称此解关于该解集为非受支配解。

多目标优化问题的本质在于各目标往往是相互冲突的，同时使多个目标均达到最优是不可能的[16]。多目标优化算法的目标就是在迭代过程中寻找尽可能多的非受支配解，最终得到问题的非受支配解集，这样可以保留所有对各目标函数不同程度侧重的解，不会丢失任一目标函数的最优值。优化结束后按用户需求从非受支配解集中选取合适的解作为最终优化结果。

2 多目标变邻域模拟退火算法

成像卫星任务规划问题已经被证明是一个非确定多项式难问题，不存在有效算法求得最优解，现有的研究都倾向于采用智能优化算法求得近似最优解，如遗传算法、蚁群算法、模拟退火算法等。其中模拟退火算法可以实现邻域搜索，且优化过程中搜索精度不断提高，很适合对成像时刻的优化。本文以成像时刻为优化对象，设计了解的编码解码和变邻域搜索策略，提出一种多目标模拟退火算法，实现对任务成像时刻的滑动优化，以达到同时优化完成任务总权重和成像质量的目的。

2.1 成像时刻的编码解码

解的编码是将任务序列表示为可被优化算法操作的对象(解)的过程，解码则是将解转化为任务序列的过程。根据1.2节对决策变量的讨论，本文设计了一种针对成像时刻的实数编码和解码方法。

1)解的编码

对于任务mi，随机生成yi：

yi=ai+ε·(bi-ai)

(11)

式中：ε∈[0,1]为随机数。式(11)可以保证yi∈[ai,bi]。将所有任务的预计成像时刻序列S=[y1,y2,…,yn]T作为优化问题的解，通过调整该时间序列达到优化任务序列的目的。

2)解的解码

将所有任务按解S表示的预计成像时刻升序排列，按时间优先的原则进行冲突处理，得到可执行任务序列。具体步骤为：

(1)将所有任务按解表示的预计成像时刻升序排列，将zi都置为1，qjk都置为0。

(12)

跳过该任务，令zi=0，重新执行步骤(2)。

(3)设卫星在时刻ei′执行完上一任务mi′，姿态矩阵为Rboi′，预计在时刻yi执行该任务，姿态矩阵为Rboi，计算机动角度

(13)

根据机动角度计算卫星所需的机动时间和执行该任务所需的资源消耗。若满足约束条件式(3)和约束条件式(4)则表示卫星可以在时刻yi观测到目标，以yi作为此任务的成像时刻，将qjk置为1，并计算卫星执行完任务mi的时间ei、更新卫星的可用资源Ej：

(14)

(4)重复步骤(2)～(3)，直到遍历完所有任务。zi为1的任务组成可执行任务序列。

对解S的解码完成后，根据式(6)和式(8)计算该解的目标函数f1和f2。

2.2 解的变邻域搜索

为实现成像时刻在时间窗口内的滑动搜索，本文设计了一个位移算子，用于调整成像时刻在时间窗口的位置。

根据模拟退火算法中接受准则的特性，温度最高时，任意两个解之间都有相同的转化概率，此时应使搜索邻域最大，使预计成像时刻可以通过位移算子到达时间窗口的任意位置，这在优化初期起到了避免陷入局部最优的“爬山”作用。随着温度的降低，模拟退火算法对差解的接受概率逐渐降低，最优解的区域也基本固定，过大的搜索邻域会使算法的优化陷入停滞。本文利用算法中的温度参数设计了一个变邻域系数来逐渐缩小搜索邻域，通过对解的微调，可以显著提高时间窗口的利用率，加快算法的收敛速度。

(15)

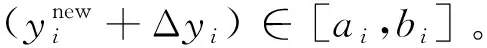
γ=tn/Tn

(16)

式中：Tn和tn分别为目标函数fn对应的初始温度和当前温度。在本文算法中，所有目标函数对应的温度采用同样的衰减系数，因此γ与n的取值无关。可以看出，γ∈(0,1]，且随温度降低不断减小。下面介绍初始温度的计算方法：

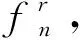
(17)

根据模拟退火算法解的接受准则[17]，可以认为在温度Tn下，任意两个解之间都有相同的转化概率。

综上，可以得到解的更新算法：

(18)

实现了成像时刻在时间窗口内的变邻域搜索。

2.3 非受支配解集的构造

本节给出多目标模拟退火算法中解的选拔淘汰机制以及非受支配解集的构造方法。

1)建立非受支配解集Nd，初始化为空集。

2)按式(17)计算目标函数f1和f2对应的初始温度T1和T2，通过调整式(8)中的α使得T1和T2在同一个数量级。

(19)

将解Sr移出Nd集，并在遍历Nd集中所有解后将解Snew加入Nd集；若有Sr≻Snew，则不改变Nd集；若Snew和Nd中的所有解都没有支配关系，直接将Snew加入Nd集。

5)若Snew≻Scur，令Scur=Snew，否则按如下概率判断是否接受新解[18]：

(20)

如果新解被接受，令Scur=Snew，否则保留当前解。

6)每执行完步骤4)～ 5)视为循环一次，若在当前温度下循环次数已经达到K，更新当前温度tn=β·tn,n=1,2，其中衰减系数β∈(0,1)。若有max{t1,t2}≤Tmin，停止优化算法，输出非受支配解集Nd，否则返回步骤4)。

以上步骤如图1所示。

图1 非受支配解集更新算法流程图Fig.1 Flow chart of the non-dominated solution set update algorithm

3 仿真校验与结果分析

为校验本文模型的有效性和算法的优势，开展对工程实例的仿真。仿真平台为：Windows 10操作系统下的Matlab，计算机配置为Intel(R) Core i7-7700HQ@ CPU 2.8 GHz处理器，16GB内存。

3.1 模型和算法参数设置

成像卫星星座有两个轨道面，每个轨道面有4颗卫星，采用太阳同步轨道。降交点地方时分别为10∶30和13∶30，以保证在降交点观测时有较好的光照条件。仿真时间为一天，即86400 s。

种子卫星轨道参数：轨道高度为500 km，偏心率为0，轨道倾角为97.4°，近地点幅角为0°，升交点赤经为160°。为保证充分利用星座的覆盖能力，每个轨道面内相邻两颗卫星相位差为90°，相邻轨道第一颗卫星相位差为45°，每个轨道面有一颗卫星为红外成像卫星，其余为可见光成像卫星。卫星最大侧摆角为45°，地面覆盖角为9.4°，星座对赤道上的点的最大重访周期约为2.95 h。考虑20个目标，总权重为60的工况，目标点随机分布在114°E～117°E、37°N～42°N之间。用户对于成像质量要求为观测时间窗口必须包含于可见时间窗口的1/4-3/4。

对于模拟退火算法，温度衰减系数β越接近1、每个温度迭代次数K越大、终止温度Tmin越低，算法的总迭代次数就越多，得到的优化结果越接近最优解，但需要的优化时间也会增加。

经过多次仿真测试，取β=0.8,K=50,Tmin=0.1时，可以在较短时间获得较好的解。

3.2 算法的可行性校验

本节通过展示单次规划的过程和结果，校验本文算法的可行性。在优化过程中，每一次降温时记录非受支配解集中的所有解对应的目标函数值，表示在二维空间中，称为每个温度下的近似Pareto面，如图2所示。图中横轴表示目标函数f1，表示任务的总权重，正方向为权重增大方向，最大值为60；纵轴表示目标函数f2，表示任务的成像质量，正方向为成像质量提高，最大值为0(对于本算例，取α=0.004，可以使两个目标函数对应的初始温度在同一数量级)。点越靠近右上，其代表的解就越优。可以看出近似Pareto面呈现向右上角层层包络的趋势，且随着温度降低，相邻温度的近似Pareto面越来越紧密，这是由于随着温度下降，搜索邻域逐渐变小，且接受差解的概率不断降低。

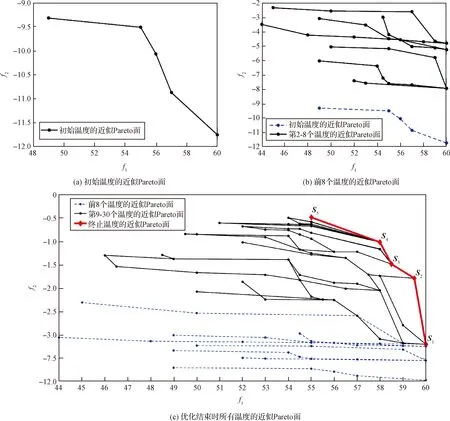
图2 多目标变邻域模拟退火算法优化过程Fig.2 Optimization process of multi-objective variable-neighborhood simulated annealing algorithm

最终优化结果为最低温度下的非受支配解集，按f1降序排列，如表1所示。最终得到的非受支配解集有5个非受支配解，这5个解表示的观测时间窗口在可见时间窗口的位置如图3所示。

表1 非受支配解的目标函数值Table 1 Objective function values of the non-dominated solutions

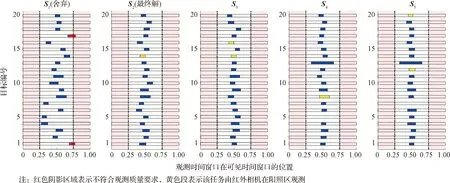
图3 非受支配解观测时间窗口位置示意图Fig.3 Observation time window represented by non-dominated solutions

可以看出由于重叠的时间窗口中执行的任务可能会相互冲突，若要使目标函数f1达到最大，将会降低一部分时间窗口的成像质量。对于每次优化得到的非受支配解集，在所有观测时间窗口必须包含于可见时间窗口1/4-3/4位置的前提下，选取任务权重最高的解作为优化的最终解。以本次优化结果为例，按完成任务总权重排序后，S1的总权重虽然最大，但有多个目标的观测窗口不符合成像质量要求(图示中的红色段)，因此舍弃S1，在剩余解中按照上述原则选择S2作为本次优化的最终解。

3.3 多种算法的比较和分析

为展示滑动优化、多目标优化、变邻域搜索在优化考虑成像质量的成像卫星任务规划问题上的优越性，将本文算法与将成像质量作为约束条件的单目标变邻域模拟退火算法(VNSA)和单目标遗传算法(GA)、考虑成像质量的单目标变邻域模拟退火算法(WOVNSA)、固定邻域的多目标模拟退火算法(MOSA)进行对比，每种算法进行20次仿真，下面用三组对比数据作进一步说明。

1)滑动优化与顺序优化

VNSA是以成像时刻为优化对象，采用实数编码实现对成像时刻的滑动优化的变邻域模拟退火算法，而GA是以观测顺序为优化对象，采用整数编码的遗传算法。VNSA和GA都是以最大化完成任务总权重为目标的单目标优化算法，其目标函数为：

(21)

成像质量要求以约束条件的方式给出，以保证观测时间窗口包含于可见时间窗口的1/4～3/4。其时间窗口为：

(22)

表2 VNSA和GA优化结果对比Table 2 Comparison of optimization results between VNSA and GA

可以看到，采用滑动优化方法的模拟退火算法从优化时间到优化效果都好于优化任务执行顺序的遗传算法，这是由于以执行顺序为优化对象的编码方式不能直接对成像时刻进行搜索，只能采用初始化的固定时刻或在冲突消解中确定，考虑到敏捷成像卫星时间窗口长，这样势必会浪费可观测时间段。

2)多目标优化与单目标优化

MOVNSA是采用基于Pareto模型的多目标变邻域模拟退火算法，WOVNSA是多目标加权的单目标变邻域模拟退火算法，其目标函数为：

(23)

λ取值越大，成像质量对优化函数的影响就越小，经过多次仿真，取λ=1.5，可以得到满足用户需求的优化效果。优化结果如表3所示。

WOVNSA相比于MOVNSA对成像质量优化效果更好，而完成任务总权重较差，这是由于其每次迭代保留的都是两个目标函数的折中解，丢失了满足

表3 MOVNSA和WOVNSA优化结果对比Table 3 Comparison of optimization results between MOVNSA and WOVNSA

用户需求的前提下的最大任务总权重的解。MOVNSA的优化结果给决策者提供了多个选择，即使用户对成像质量的需求发生变化，仍可在非受支配解集中选取最优解。

3)变邻域与定邻域搜索

MOVNSA是采用变邻域搜索的多目标模拟退火算法，而MOSA是采用定邻域(γ=0.5)搜索的多目标模拟退火算法，优化结果如表4所示。

表4 MOVNSA和MOSA优化结果对比Table 4 Comparison of optimization results between MOVNSA and MOSA

定邻域的模拟退火算法的效果不佳，这是由于温度较高时搜索范围过小，无法跳出局部最优，而温度较低时，接受差解的概率变低，过大的搜索范围难以改善当前解，因此定邻域模拟退火算法在优化过程中存在停滞的现象。定邻域模拟退火算法的优化过程如图4所示。

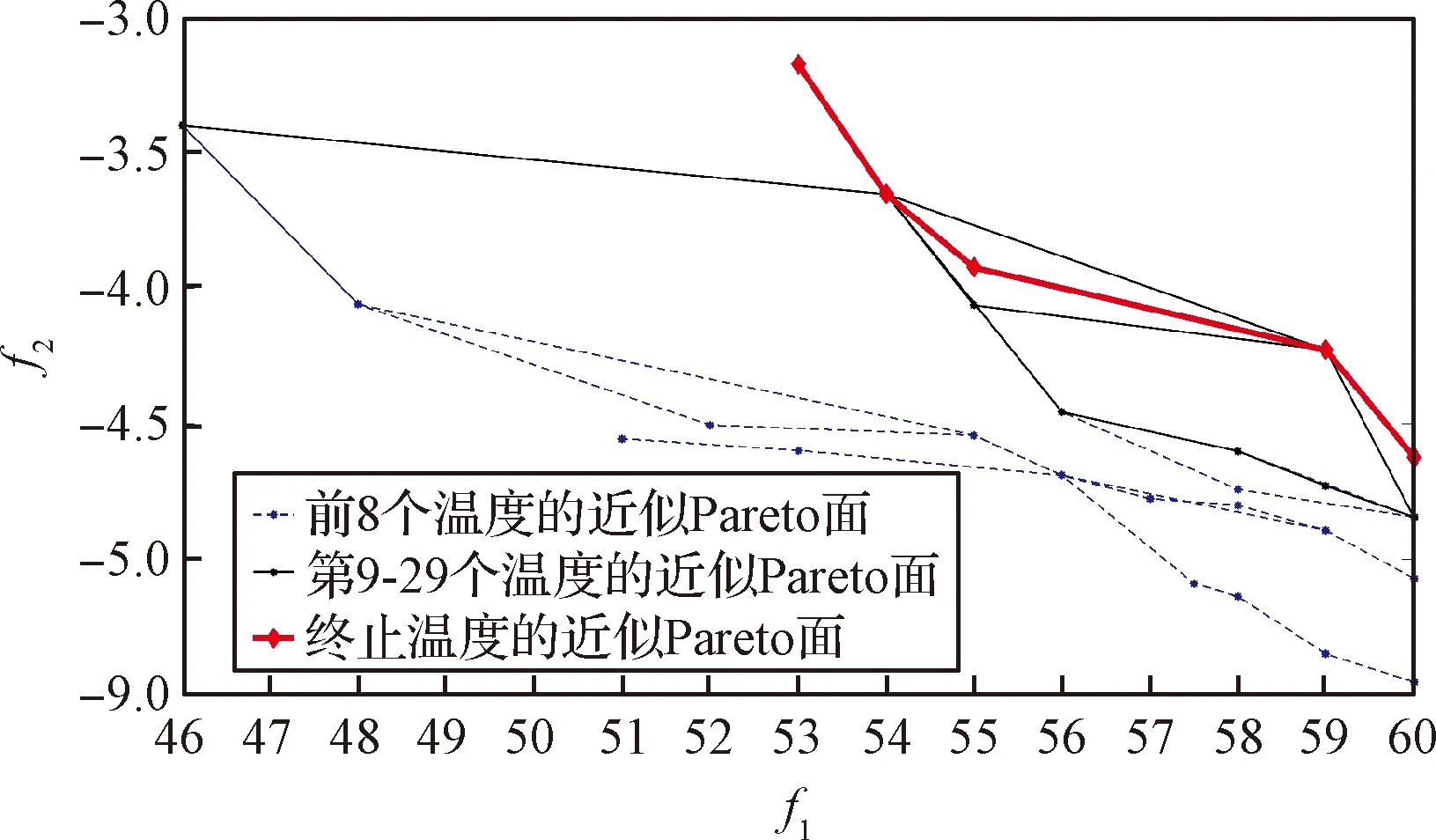
图4 多目标定邻域模拟退火算法优化过程Fig.4 Optimization process of multi-objective fixed-neighborhood simulated annealing algorithm

将图4与图2 (c)对比可以看出，随着优化的不断进行，定邻域模拟退火算法的相邻温度近似Pareto面趋于重合，不能有效改善非受支配解集。

综上所述，以成像时刻为优化对象的变邻域模拟退火算法相比于以任务顺序为优化对象的遗传算法，大大提高了优化效率，并且可以有效的优化成像质量；其中多目标模拟退火算法既可以兼顾最大化完成任务总权重和提高成像质量，还可以给决策者多种选择，根据用户需求选择最优解。

4 结 论

本文以最大化任务完成度和满足用户成像质量为目标，建立了多星协同的敏捷成像卫星观测任务模型。设计了一种以成像时刻为优化对象的滑动优化策略，迭代过程中对每个任务的成像时刻进行邻域搜索，可以兼顾优化单任务观测时间段在可见时间窗口的位置和优化相邻任务的观测顺序。采用多目标模拟退火算法求解该多目标优化问题，利用模拟退火算法中的降温过程不断缩小搜索范围，显著改善了算法的优化效果。仿真结果表明本文算法收敛速度快，优化效果好，可以在满足用户需求的前提下最大化完成任务总权重。