基于方位各向异性的裂缝密度反演方法及应用

陈超，印兴耀，刘晓晶，马正乾

1 中国石油大学(华东)地球科学与技术学院,青岛 266580 2 中国石化勘探分公司，成都 610041

0 引言

长期以来，裂缝预测一直是油气地球物理的重要研究内容,在非常规储层中的作用也越发重要.近年来北美及中国页岩气的勘探开发揭示了裂缝的重要性(何治亮等,2020)，普遍认为天然裂缝具有良好的结构弱面，强度较低，有利于降低破裂压力形成复杂缝网，是影响压裂效果的关键因素(Guo et al.,2018;Chang et al.,2018)，是页岩气甜点预测的关键参数.Rüger(1996)对各向异性介质反射特征进行了研究，推导出各向异性反射系数近似方程.振幅随偏移距及方位角变化特征分析已经成为油气储层预测的重要手段.当前基于地震各向异性理论识别地下裂缝的技术已经取得了较好的应用效果，发展了基于方位属性、方位弹性阻抗及各向异性梯度等预测技术(Chen et al.,2020;Guo et al.,2019;Li et al.,2020).

方位各向异性地震反演是获取裂缝密度的重要手段(Xue et al.,2017；王赟等，2017；Pan et al.,2020a)，方位AVO特征已经被证明可用于裂缝预测，前人做了大量基础性研究(印兴耀等，2014,2020；Chen et al.,2015；Wang et al.,2019).目前常用的裂缝介质模型主要为Hudson(1980，1986)和Thomsen(1986，1995)的微小裂隙理论模型，以及Schoenberg(1983)提出的线性滑移理论模型.Thomsen以及Schoenberg明确了裂缝介质的各向异性特征，提出了各向异性参数ε、γ、δ及法向弱度ΔN和切向弱度ΔT.考虑充填裂缝的具有水平对称轴的横向各向同性介质(HTI介质)，Bakulin(2000)认为Hudson理论和Schoenberg研究的是同一种裂缝介质，因此他们的弹性矩阵应该是一致的，推导了各向异性参数(ε(v)、δ(v)、γ(v))与 Schoenberg弱度参数(ΔN、ΔT)及裂缝密度(e)之间的关系.前人也对各向异性参数以及裂缝弱度在不同裂缝充填流体类型、不同裂缝密度以及不同裂缝纵横比情况下的变化特征做了大量研究(Chen et al.,2015;Chapman,2009;Quintal et al.,2011)，认为裂缝充填物的变化对ΔT影响不大.

建立裂缝岩石物理参数与地震反射系数间的关系，是实现裂缝密度地震预测的基础(Downton and Roure,2015;Pan et al.,2020b;Zhang and Li,2013)，Rüger(1996)根据一阶扰动理论给出了HTI介质包含各向异性参数的方位AVO的反射系数近似方程，为后续各向异性研究奠定了基础.目前叠前地震裂缝预测技术主要可以分为两种.第一是直接基于方位地震数据的振幅、频率及衰减等属性直接开展裂缝预测，认为方位反射振幅近似是一条周期为π的余弦曲线，Al-Marzoug(2006)将方位AVO梯度拟合成椭圆,预测裂缝密度及方向，Downton和Roure (2015)将方位AVO近似方程进行傅里叶级数展开预测裂缝，上述方法实际是利用的反射界面信息，不能完全代表目的层的裂缝发育情况.第二类方法是借用Connolly(1999)率先提出的弹性阻抗的概念，将反射界面信息转换为含裂缝的弹性参数信息，进而开展裂缝预测，或者直接反演得到各向异性参数(张峰和李向阳，2015;Zhang and Li,2016).Pan 等(2021)、Li等(2020)、Ma等(2019)等人在岩石物理模型驱动下开展了各向异性参数反演研究,取得一定的效果，但存在预测结果横向连续性差，对低频模型依赖度高等问题.

本文首先明确了四川盆地五峰组—龙马溪组页岩气储层多发育高角度裂缝，具有明显的HTI特征，符合上述理论模型；且裂缝密度与法向弱度ΔN、切向弱度ΔT及剪切模量密切相关，具备通过各向异性参数反演裂缝密度的理论基础.然后建立了一种新的能反映裂缝密度的近似公式，同时推导了相应的方位弹性阻抗方程(EVVAz方程)，应用贝叶斯理论，提出了一种新的裂缝密度反演方法.实际工区应用表明该方法稳定、可靠，预测结果表明裂缝发育密度与破裂压力呈一定的负相关性，预测结果可为页岩气可压性评价提供可行的依据.

1 方法原理

1.1 裂缝密度表征

等效介质理论中，裂缝的表征可以通过占比表示，包括各向异性SCA(Self-consistent approximations，自洽模型)、各向异性DEM(Differential effective medium，微分等效介质模型)用的体积分数表达式.裂缝密度一般以每米岩心长度上有多少条裂缝来表示，也可以用单位岩心表面积中裂缝的截面积来表示，通过建立等效模型来简化裂缝密度，Hudson(1980，1986)针对硬币状裂缝开展研究，并给出了裂缝密度、裂缝孔隙度计算方法：

(1)

其中，e为裂缝密度；φf为裂缝孔隙度；Vf为裂缝的体积，Va为井筒的体积，可以通过FMI成像测井计算获得；为裂缝的纵横比，根据Hudson硬币状裂缝赋值.

考虑充填裂缝的具有水平对称轴的横向各向同性介质(HTI介质)，Bakulin等(2000)根据弹性矩阵的一致性推导了各向异性参数ε(v)、δ(v)、γ与Schoenberg裂缝模型的法向和切向弱度之间的关系：

(2)

其中，g=μ/(λ+2μ)，λ和μ分别为含裂缝背景介质的拉梅参数与剪切模量；ΔN、ΔT分别为裂缝的法向弱度与切向弱度.

假设裂缝充填某种弱介质，其体积模量和剪切模量分别为k′和μ′，则裂缝的法向弱度和切向弱度可通过下式进行计算(Hudson,1980 and Schoenberg,1993)：

(3)

根据(3)式，由法向弱度ΔN和切向弱度ΔT可分别求得裂缝密度：

(4)

其中，eΔN、eΔT分别表示由法向、切向弱度导出的裂缝密度.

由上式可知，在求取得到裂缝法向、切向弱度以及背景介质剪切模量的条件下可计算得到裂缝密度.通常的方法是根据Rüger近似开展叠前地震反演求得纵波速度、横波速度、Thomsen各向异性参数后，再根据基本的岩石物理关系进行转换，代入上式中分别进行裂缝密度求取.这种方法存在多次转换，误差在计算过程中累计，预测精度将降低.通过基本岩石物理理论将Rüger近似重新推导为包含拉梅参数、剪切模量、法向弱度、切向弱度的近似方程，直接反演裂缝参数减小累计误差.最后，将裂缝密度表示为eΔN、eΔT的加权平均：

e=feΔN+(1-f)eΔT,

(5)

其中，f为加权因子，0≤f≤1，该加权因子的主要作用是调节法向和切向弱度参数的贡献度，本文研究中均给0.5.

1.2 含裂缝参数的EVAAz方程

在HTI介质中，在非零入射角下，不同方位地震波速度表现出差异性，因此地震振幅随方位变化.Rüger(1998)根据一阶扰动理论给出了HTI介质的方位AVO的反射系数近似方程，具体形式如下式所示：

(6)

Rp(θ,φ)=Riso+Rani,

(7)

其中，

(8)

×Δδ(V)+4gsin2θcos2φΔγ,

(9)

直接利用上式反演得到地层纵波速度、横波速度、密度、各向异性参数，进而再利用(2)、(3)可间接计算得到裂缝密度参数e.但间接反演，存在累计误差进而导致预测精度降低.为了提高预测精度，本文针对(7)式进一步简化.

(10)

将(2)式中各式代入(9)式可以得到关于法向弱度ΔN和切向弱度ΔT的各向异性反射系数扰动项：

Rani=[-g(1-2g)cos2φsin2θ-gcos2φ[(1-2g)sin2φ+(1-g)cos2φ]sin2θtan2θ](ΔΔN)

+(gcos2φsin2θ-gcos2φsin2φsin2θtan2θ)ΔΔT,

(11)

由于Rüger近似中介质基本模型为上半空间为各向同性，下半空间为裂缝发育介质，因此，

(12)

因此(11)式可以进一步近似写为

Rani=[-g(1-2g)cos2φsin2θ-gcos2φ[(1-2g)sin2φ+(1-g)cos2φ]sin2θtan2θ](ΔN)

+(gcos2φsin2θ-gcos2φsin2φsin2θtan2θ)ΔT,

(13)

将(10)式、(13)式代入(7)式即可得到新的反射系数近似方程：

+D(θ,φ)ΔN+E(θ,φ)ΔT,

(14)

其中

(15)

设计了一个HTI介质模型(表1)用于验证公式(14)的正确性.页岩储层发育高角度缝，用各向异性参数(δ(v)、ε(v)、γ)进行了表示，且计算了裂缝的法向弱度ΔN和切向弱度ΔT，同时设计顶板为各向同性的页岩，底板为各向同性的灰岩.在此基础上分析了推导的各向异性反射系数近似公式(14)的合理性，并与Rüger近似公式(6)进行了对比，计算结果如图1，明显看出HTI介质页岩储层底界的反射系数随方位角的周期性变化规律，且两者计算的反射系数几乎重合(曲线为Rüger近似公式结果，散点为公式(14)的结果)，说明公式(14)满足各向异性反演的要求.图1中蓝色曲线、绿色曲线、红色曲线分别表示在入射角等于10°、20°、30°时反射系数随方位角的变化规律，对比两者明显看出较大入射角反射系数的方位周期性变化特征更为明显.

表1 地层弹性参数与各向异性参数Table 1 Formation elastic parameters and anisotropy parameters

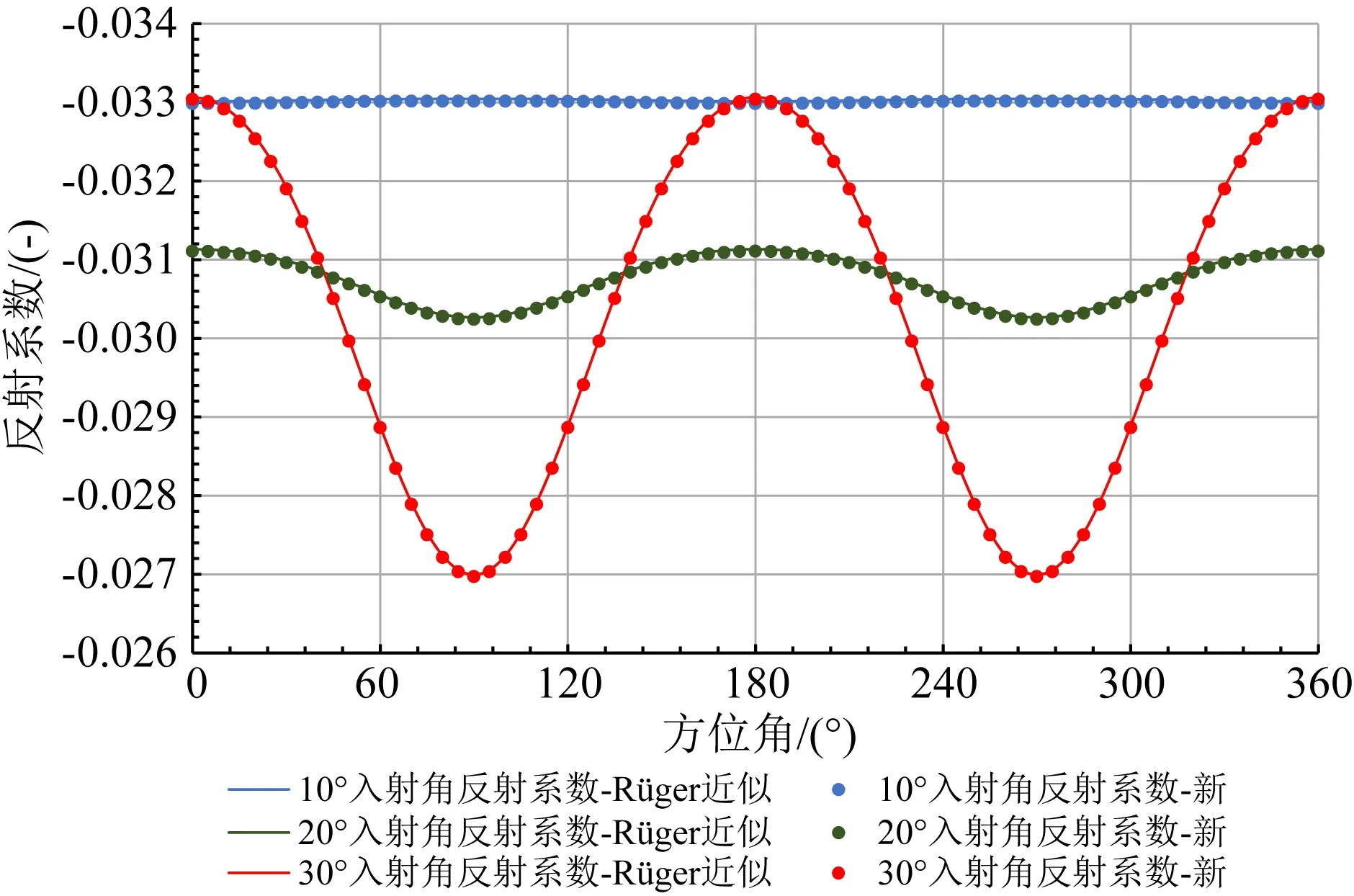
图1 不同入射角Rüger近似公式与新公式反射系数随方位角变化对比Fig.1 Comparisons between results of computed Rp(θ,φ)using new and original equations

新推导的反射系数近似方程(14)式与(7)式相比，待反演参数的维度从6降为5，这对反演的稳定性提升具有一定的优势.基于上式可以直接反演得到λ、μ、ΔN、ΔT，减少累计误差，提高预测精度.

由于弹性阻抗反演稳定性高，在实际生产中得到了广泛的应用.根据Connolly(1999)推导弹性阻抗以及Whitcombe(2002)标准化弹性阻抗的思想，将方程(14)推导为方位弹性阻抗方程，即表示为弹性阻抗随着入射角及方位角的变化方程(EVAAz方程)：

×exp[d(θ,φ)ΔN]×exp[e(θ,φ)ΔT],

(16)

其中，EI0、λ0、μ0、ρ0分别为弹性阻抗、拉梅参数、剪切模量、密度的平均值，a(θ)、b(θ)、c(θ)、d(θ,φ)、e(θ,φ)分别表示为：

为了更为直观地展示方位弹性阻抗与各向同性介质中弹性阻抗的区别，我们选取两层模型对弹性阻抗随方位和入射角的变化进行了分析，地层参数详见表1，其中上覆盖层为各向同性地层，储层为近垂向排列的裂缝型储层.在各向同性地层中，弹性阻抗仅随入射角发生变化，随方位角不变(图2a)；裂缝发育地层中，弹性阻抗同时随入射角与方位角发生变化，可利用弹性阻抗随入射角与方位角的变化开展各向异性参数反演方法的研究，从图2b中可以看出，随着入射角的增大，方位弹性阻抗随方位角的周期性变化更为明显，说明充分利用大入射角的信息是开展各向异性参数反演的基础.

图2 方位弹性阻抗随入射角和方位角的变化趋势(a)上覆盖层方位弹性阻抗;(b)裂缝型储层方位弹性阻抗.Fig.2 Trend of azimuth elastic impedance with incident angle and azimuth angle(a)Azimuth elastic impedance of the overlying caprock;(b)Azimuth elastic impedance of fractured reservoir.

1.3 裂缝密度EVAAz反演

R(φ2,θM,ti),…R(φH,θM,ti)…R(φH,θM,ti)]

=[mimi+N…mi+HMN],(i=1,2,…,N)

(17)

(18)

在反演中，为了增强反演的稳定性，补充低频信息，还需要考虑低频模型约束：

(19)

假设地面地震的观测数据向量d的噪声n服从均值为0、协方差矩阵为Xn的高斯分布，则地面观测叠前地震数据d与模型参数m之间的似然函数可利用噪声的分布特征进行表示(印兴耀等，2013)：

(20)

在贝叶斯框架下，待反演模型参数m的后验概率分布：

p(m|d)∝p(m)p(d|m)=pmc(m)pLFM(m)p(d|m),

(21)

其中，p(m|d)为后验概率，p(d|m)为似然函数，p(m)为模型参数的先验概率.

在后验概率极大条件下求得目标函数如下式所示：

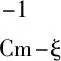
(22)

对上式求解得到不同方位角、不同入射角的弹性阻抗数据体.同时，为了便于求解裂缝参数，首先对(16)式进行线性化处理：

+d(θ,φ)ΔN+e(θ,φ)ΔT.

(23)

对于单道的方位弹性阻抗数据存在N个采样点，定义

对于存在H个方位角、M个入射角时，则可将(23)式联立形成方程组，写作矩阵的形式：

L=Bx,

(24)

其中，L为方位弹性阻抗组成的列向量；B为(23)式中系数组成的矩阵；x为待反演参数组成的列向量：

通过阻尼最小二乘算法即可对(24)式进行求解：

x=(BTB+αI)-1BTL,

(25)

其中，α为阻尼因子，控制反演的稳定性，I∈RH MN×H MN为单位矩阵.

在得到不同方位角、不同入射角的弹性阻抗数据体基础上，即可根据公式(25)求取λ、μ、ΔN、ΔT，最终应用公式(4)(5)可得裂缝密度，为更加清晰地阐述实际资料处理过程，在此附流程图(图3).

图3 HTI介质裂缝密度反演流程Fig.3 HTI media crack density inversion process

2 模型测试及实际应用

2.1 正演分析

利用实钻井测井数据纵波速度、横波速度、密度和各向异性曲线，计算了单井剪切模量μ和拉梅系数λ曲线，并应用公式(16)计算了不同入射角(10°、20°、30°)和不同方位角(15°、75°、135°)的弹性阻抗曲线(图4).图5中红色曲线分别为利用本文基于不同入射角和方位角弹性阻抗反演公式(25)提取的拉梅系数λ、剪切模量μ、密度ρ、法向弱度ΔN与切向弱度ΔT，黑色曲线为测井曲线计算得到的λ、μ、ρ、ΔN与ΔT，比较反演结果与原始模型可以发现两者几乎重合,误差很小.

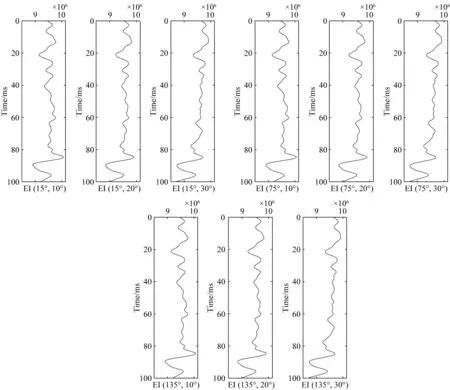
图4 不同入射角及方位角弹性阻抗曲线(EI(a°,b°)中a°指方位角，b°入射角)Fig.4 Elastic impedance curves with different incident angles and azimuth angles

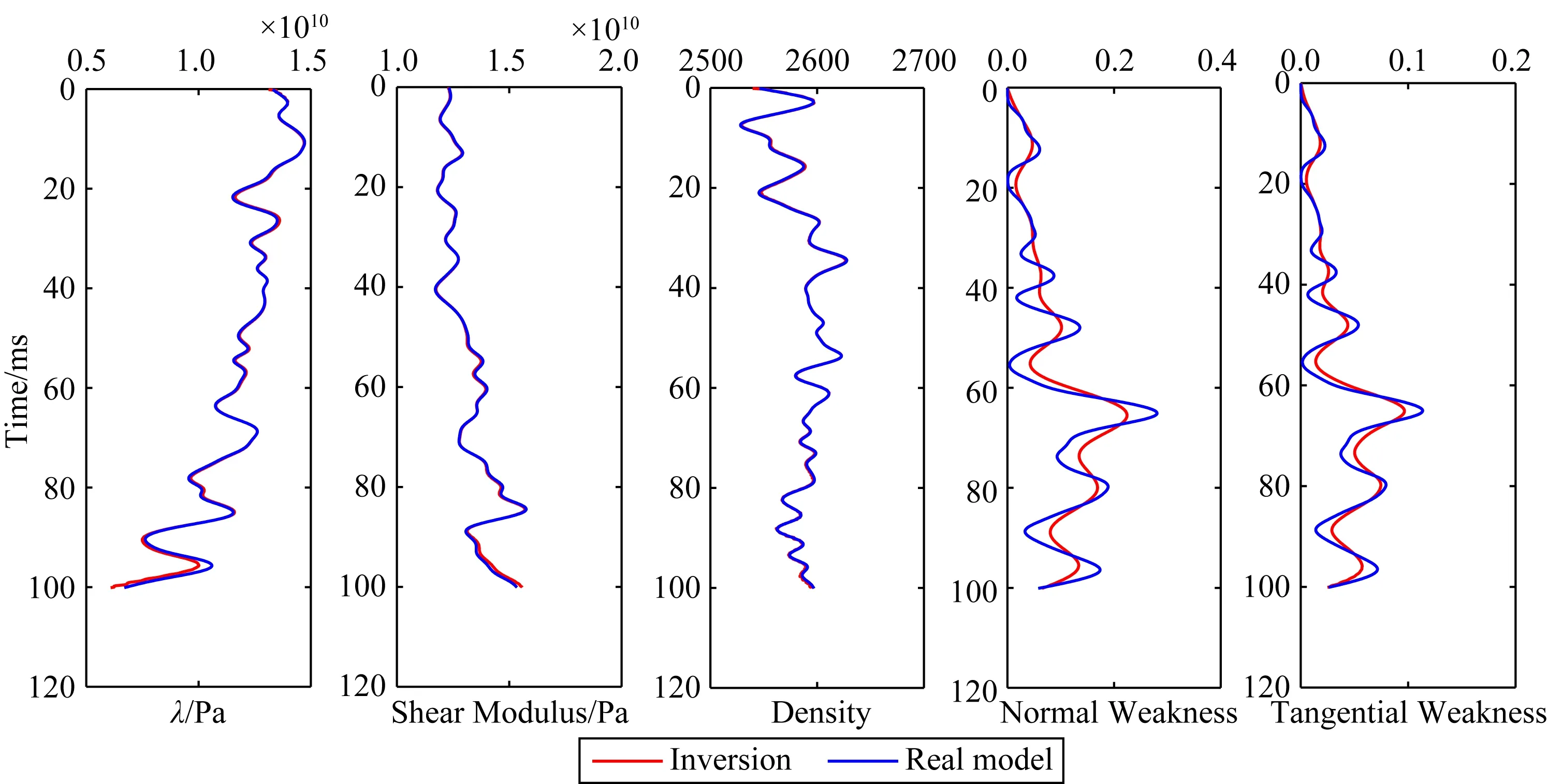
图5 拉梅系数λ、剪切模量μ、密度ρ、法向弱度ΔN与切向弱度ΔT反演曲线与真实模型对比Fig.5 Comparison of inversion curves of Lame coefficient,shear modulus,density,normal and tangential weakness with real model

实际应用中,弹性阻抗由地震数据反演得到，不可避免会含有噪声.因此，为了测试利用方位弹性阻抗提取λ、μ、ρ、ΔN与ΔT对噪声的敏感性，向方位地震数据加入10∶1的噪声，并反演相应的方位弹性阻抗数据(图6)，再次提取的λ、μ、ρ、ΔN与ΔT分别如图7中红色曲线所示，可以发现，随着噪声的增加，提取的λ、μ、ρ、ΔN与ΔT中的噪声也会增加，精度有所降低，但反演结果依然与原始模型具有很高的吻合度.因此，利用本文的方法可以稳定、可靠地提取λ、μ、ρ、ΔN与ΔT，该反演方法能利用叠前地震资料反演得到裂缝性储层的弱度参数和裂缝密度.

图6 不同入射角及方位角弹性阻抗曲线(加入10∶1的噪声)Fig.6 Elastic impedance curves with different incident angles and azimuth angles (Noise with 10∶1 ratio)

图7 拉梅系数λ、剪切模量μ、密度ρ、法向弱度ΔN与切向弱度ΔT反演曲线与真实模型对比(加入10∶1的噪声)Fig.7 Comparison of inversion curves of Lame coefficient,shear modulus,density,normal and tangential weakness with real model (Noise with 10∶1 ratio)

2.2 裂缝密度反演

研究区位于四川盆地五峰组—龙马溪组，页岩脆性矿物含量高，在构造应力作用下，易于产生微裂缝，岩心中可见普遍发育的高角度缝，FMI成像测井同样显示大量高角度裂缝的发育，整体具有明显的HTI介质特征，这些微裂缝的发育对于页岩的压裂至关重要.基于FMI成像测井解释成果,应用公式(1)，即可求得井筒的裂缝孔隙度及裂缝密度曲线，给定裂缝包含物的模量，实际研究区高导缝发育，以干气充填为主，利用公式(3)，即可计算得到裂缝的法向弱度与切向弱度(图8).

图8 岩层地层高角度裂缝孔隙度、裂缝密度及弱度参数曲线Fig.8 High-angle fracture porosity,fracture density and anisotropy parameter curve of rock strata

根据研究区页岩的HTI介质特征，对ΔN及ΔT与裂缝密度的相关性进行了分析(图9)，青色为ΔT与裂缝密度相关曲线，蓝色为ΔN与裂缝密度相关曲线，ΔN及ΔT均随着裂缝密度e的增加而增加，呈良好的正相关关系，利用ΔN及ΔT均可以实现对裂缝密度的有效预测.

图9 ΔN、ΔT与裂缝密度的相关图Fig.9 Correlation diagram between ΔN and ΔT and fracture density

本文研究区拥有全方位三维地震，并开展了OVT域处理，获得了高品质的五维叠前道集数据.综合各方位覆盖次数、最大偏移距，将OVT叠前道集等分为6个方位的角度道集，并对每个方位道集划分为3个入射角部分叠加，总共得到18个不同方位、不同入射角的地震数据，对所有数据开展组稀疏方位弹性阻抗反演，在弹性阻抗反演的基础上实现弱度参数预测.不同方位的大中小入射角叠加地震剖面如图10所示，研究区资料入射角最大可达35°，结合叠前道集品质，确定小角度入射角范围5°～13°，反演中取9°，中角度入射角范围14°～22°，反演中取18°，大角度入射角范围23°～31°，反演中取27°.图11为反演得到的不同方位的大中小入射角弹性阻抗，反演结果表现出明显的差异性.

图10 不同观测方位、不同入射角地震数据Fig.10 Seismic data of different observation azimuths and different incident angles

在不同方位不同入射角弹性阻抗反演的基础上，将图11中所有的弹性阻抗体取对数，按照公式(23)(24)，通过阻尼最小二乘算法，求得目的层的μ、ΔN及ΔT(图12).图12b和图12c分别为法向弱度ΔN及切向弱度ΔT反演剖面，明显可以看出页岩层段ΔN及ΔT值为0.1～0.3左右，与井点处实际结果较为吻合(图中黑线曲线).最后利用公式(4)(5)最终就可求得裂缝密度(图13).

图11 不同观测方位、不同入射角组稀疏弹性阻抗反演结果Fig.11 Inversion results of sparse elastic impedance in different observation azimuths and different incidence angle

图12 剪切模量、ΔN及ΔT反演结果Fig.12 Inversion results of shear modulus,ΔN and ΔT

图13为过实际水平井的裂缝预测剖面图，从图中可以看出，水平井轨迹中间9—21段裂缝密度相对较大为红色，值多大于0.05，对比分析该井水力压裂过程中的破裂压力曲线(图13中红色曲线)，明显看出11—20段破裂压力显著降低，两者基本吻合，说明了裂缝面多为弱面，易于破裂.该方法能实现裂缝密度的直接预测，效果显著，预测结果与压裂施工参数及测试结果具有较好的吻合程度，为页岩气水平井钻后压裂效果评估提供了有力支撑，预测成果也为后期井位部署及设计提供了参考基础.

图13 裂缝密度反演结果Fig.13 Fracture density inversion results

3 结论

页岩储层微裂缝发育有利于降低压裂难度，具有明显的HTI介质方位各向异性特征，裂缝的地震预测是页岩气甜点预测的重要研究内容，反演弱度参数是实现裂缝定量预测的重要手段.本文推导了一种能反映裂缝密度的方位AVO近似公式及其方位弹性阻抗方程，通过贝叶斯理论实现了介质的弹性参数及弱度参数的联合反演，再利用弱度与裂缝密度的相关性，实现了裂缝密度定量预测.并得出以下四点结论：

(1)联合Rüger提出的方位AVO反射系数近似方程及面向剪切模量的Gray反射系数近似公式，建立的方位AVO近似公式是裂缝介质剪切模量、密度、拉梅参数及裂缝弱度参数的函数，降低了待反演参数的维度，可提高反演的稳定性.

(2)利用方位弹性阻抗反演更稳定的特点，同时基于贝叶斯理论框架，建立组稀疏弹性阻抗反演目标函数，可以保证不同方位弹性阻抗采样点一致性，能够进一步提高反演的精度.

(3)在不同方位不同入射角弹性阻抗反演的基础上，通过阻尼最小二乘算法，实现裂缝介质剪切模量与弱度参数的联合反演，进而预测裂缝密度，经实际数据试验，预测结果与页岩压裂参数吻合度高，该方法是有效的.

(4)页岩储层裂缝发育密度与破裂压力呈一定的负相关性，裂缝越发育，破裂压力越低，裂缝发育有利于产能的提高，预测成果可以为钻井设计及工程压裂提供有效的指导.

致谢感谢审稿人提出的宝贵修改建议.