地震动旋转分量用于矩张量反演的数值试验

华思博，张勇

北京大学地球与空间科学学院，北京 100871

0 引言

地震波由震源激发，在地球内部介质中传播，介质在地震波作用下发生的运动通常包括平移运动、旋转运动和体积形变(Trifunac，2009).传统地震学主要观测平动记录，在此基础上开展相关的模拟和反演工作，但要想完整地描述地震波作用下的介质运动过程，不仅需要平动，还需要旋转(Aki and Richards，2002；Lee et al.，2009).地震波旋转的理论、观测和分析研究在地震学中具有重要意义(顾浩鼎和陈运泰，1988；刘庚等，2020).事实上，一百年前就有研究者观测到了由地震产生的旋转效应，但受限于当时的仪器水平，无法进行准确测量.旋转的振幅比平动一般要低若干数量级，导致其很长一段时间都未被重视，大多地震学研究仍以平动研究为主(张佩等，2018).

近些年来随着地震观测技术的发展，人们设计制造了越来越精确的旋转地震仪，以此积累了越来越多的地面旋转记录(Lee et al.，2009；董兴朋等，2013).目前获得旋转记录的手段有两类，一类为根据台阵平动进行差分得到旋转(王君杰和胡聿贤，1991；何超等，2011；周佩佩和巢斯，2013)；另一类为直接观测，比如利用激光陀螺仪(Takeo，1998；Igel et al.，2005，2007；Huang et al.,2006)和利用光纤技术测量地面的旋转运动(Schreiber et al.,2009;Bernauer et al.,2012)，以及利用地面倾斜数据构建旋转波场(周聪等，2019).有关旋转的理论研究也在近些年得到了进一步发展，比如远震旋转勒夫波层析成像(Takeo，1998)、地球自由震荡的旋转观测(Igel et al.，2011)以及旋转噪声成像等(Hadziioannou et al.，2012).随着旋转观测技术的发展和旋转地震波理论的成熟，旋转地震波越来越得到重视，其应用也越来越广泛.可以预期，未来旋转观测数据完全可能成为和平动记录一样普遍的地震波数据类型，应用于震源反演及地球介质成像等常规地震学研究工作中.

在震源反演中，平动分量和旋转分量能否联合反演，其效果如何，值得预先进行探究.在这方面，已经有学者对利用旋转和平动记录对震源反演开展了初步的数值试验，如Bernauer 等(2014)和Reinwald等(2016)利用贝叶斯反演的方法，探究在有限断层反演中利用旋转和平动进行联合反演的效果，发现加入旋转分量可以更好地约束破裂过程，降低结果非唯一性.此外，也有学者应用贝叶斯反演的方法对在矩张量反演中加入旋转分量进行了数值试验(Donner et al.，2016，2018，2020)，发现旋转分量可以更好地约束矩心深度，同时改善对矩张量某些元素的约束.

然而现有的将旋转用于矩张量反演的数值试验都是基于简单震源时间函数(δ函数)，针对特定或少数几种震源机制进行反演，对震源机制、震源时间函数的复杂性和典型台站分布未给予充分考虑.本研究将从更一般的角度出发，对双力偶震源机制所有可能的走向、倾角和滑动角做等间距采样，以保证矩张量的完备性；同时采用复杂的震源时间函数，尽可能真实地模拟实际的震源过程；针对不同的典型台站分布、频段和信噪比等情况开展更为系统和全面的数值试验，得到更具代表性和普适性的认识.

1 均匀无限空间中地震波的旋转分量与平动分量的辐射花样

地震动的旋转可由其平动的空间旋度得到(Aki and Richards，2002；张海明，2021).在均匀无限空间中，纯剪切位错源激发的旋转地震波场可以表示为(Suryanto,2006;Cochard et al.,2006;周聪等,2019)：

(1)

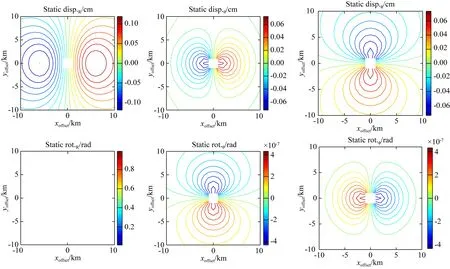
图1 均匀无限空间中位错点源激发的静态位移和旋转场(Suryanto,2006)Fig.1 The distribution of the static displacement and rotation excited by a dislocation point source in a homogeneous infinite space (Suryanto,2006)

平动和旋转分量辐射花样的互补性显示：在平动分量的基础上引入旋转分量可能为地震震源参数提供更好的约束，从而得到更可靠的反演结果.因为在反演过程中，如果某个矩张量元素激发的波形振幅远小于其他矩张量元素，则该元素可能无法得到有效的约束(Dziewonski et al.，1981；Bukchin et al.，2010).在台站非常稀疏时，所有平动分量可能都无法有效约束某个矩张量元素，这时如果在相同台站处引入旋转分量，完全可能提升对该矩张量元素的约束能力.基于以上分析与认识，我们设计了本文的数值试验.

2 研究方案

2.1 平动与旋转波形的正演计算

在同步源的假设下，地震在n方向产生的位移和旋转可分别表示为：

un(t)=Mpq·stf(t)*Gnp,q(t),

(2)

wn(t)=Mpq·stf(t)*Hnp,q(t),

(3)

其中stf(t)为震源时间函数，Gnp,q(t)为震源处的力偶Mpq在此台站处激发的平动n分量格林函数，Hnp,q(t)为相应的旋转格林函数，‘*’为卷积符号，除特殊说明外，所有公式均采用爱因斯坦求和约定.

本文基于一维速度结构模型(见图2b和图2c)，采用QSSP2017(Wang et al.，2017)计算平动和旋转格林函数(Gnp,q和Hnp,q).选取图2a所示持续时间为20 s的面积归一化的复杂震源时间函数作为stf(t)，对双力偶震源的断层参数进行均匀采样，以5°为间距，走向从0°到175°，倾角从0°到90°，滑动角从 0°到175°，得到24624个纯剪切位错的矩张量，并按照(2)和(3)式计算平动和旋转波形.需要说明的是，我们没必要对走向和滑动角的所有取值范围(0°～360°)采样，因为在其他条件不变的情况下，走向或滑动角加180°只改变合成波形的极性，而不改变其波形形态.为模拟地震观测误差，我们在合成的平动和旋转波形中均添加了高斯随机噪声.除后文对信噪比进行特殊讨论外，添加噪声后所有波形的信噪比均为10.通过以上步骤，得到了用于后文反演的合成平动和旋转波形.研究考虑了几种典型的台站分布，震源均位于(0°,0°)，震源深度为10 km(图3).

图2 用于数值试验的部分条件(a)用于正演的面积归一化震源时间函数；(b)P波速度结构模型，蓝色和红色分别为准确速度结构和有误差的速度结构；(c)同(b)但为S波.Fig.2 Conditions used in the numerical experiment(a)Area-normalized source time function used for the forward model;(b)P wave velocity model,the blue and red lines denote the original and the adjusted velocity model,respectively;(c)Similar to (b)but for S wave.

图3 数值试验中用到的各种台站分布(a)单台;(b)北南双台;(c)北东双台;(d)北东南西四台;(e)32台.其中红色三角形代表加旋转分量且保持总记录数量不变时选择的台站，即在红色台站添加旋转来替换蓝色台站的平动，黄色五角星为震中位置.Fig.3 Station distributions used in the numerical experiments(a)Single station;(b)Double stations in the north and the south;(c)Double stations in the north and the east;(d)4 stations in the north,the east,the south and the west;(e)32 stations.The red triangles denote the chosen stations when we keep the total record quantity unchanged,which means we add rotational components to the red stations to replace translational components in blue stations. The yellow stars are the epicenters.

2.2 用平动与旋转进行矩张量反演

我们将2.1节合成的平动和旋转波形作为数据，结合Global Centroid Moment Tensor (GCMT)和United States Geological Survey(USGS)等机构的震源机制反演流程(Ekström et al.,2005)进行矩张量反演，将震源时间函数简化为一个等腰三角形，由起始时间ts和半宽tr两个参数控制.对矩心深度d以及ts和tr进行格点搜索，d的范围为6～15 km，步长为1 km，ts为0～6 s，tr为2～9 s，二者步长均为1 s.每次搜索中的线性反演矩阵可表示为

[STF(ts,tr)*Knp,q(d)][Mpq]=[A],

(4)

其中STF(ts,tr)为每次格点搜索中由ts和tr合成的等腰三角形震源时间函数，A为正演合成的波形，Kn p,q(d)为对应此搜索深度的格林函数矩阵，包含了位移格林函数Gn p,q和旋转格林函数Hn p,q，Mpq为待求解的矩张量.取此矩阵方程的最小二乘解为此格点条件下的矩张量反演结果，并计算归一化的波形反演残差Misfit

(5)

其中obs为正演合成的波形，syn为根据反演结果计算得到的波形.对于每个矩张量的反演，在每个反演深度下，取使Misfit最小的ts、tr组合，在此情况下得到此深度下该矩张量的反演结果，最后将不同深度下的24624个矩张量反演结果的平均Misfit进行比较.除对频段的专门讨论外，反演中使用的频段均为0.005～0.02 Hz，采样率为1 Hz，波形长度为360 s，由于平动振幅和旋转振幅相差数个量级，我们对所有波形进行了能量平权处理(即所有波形和对应的格林函数在反演前都除以其波形的平方和)，平权后以1∶1的权重进行反演，以确保反演时平动波形和旋转波形的振幅大体相当.

本文针对不同台站分量分布的情况进行考察，尝试了三种台站分量分布情况：①只用平动分量单独反演，②在平动分量的基础上加上旋转分量进行联合反演，以及③在总波形数量不变的前提下(即在部分台站添加旋转分量替换其他台站的平动分量)进行联合反演.对于不同台站分量的情况，我们主要从以下几个方面对得到的结果进行评估.一是反演得到的每个矩张量元素与输入值的误差，观察不同情况下的误差分布直方图，并用正态分布拟合，得到均值μ与标准差σ；二是针对矩张量整体的差异，根据Kagan(1992)中描述的矩张量的相关性，由矩张量差异角Δφ及反演得到的地震矩M0(Silver and Jordon,1982)来进行评价：

(6)

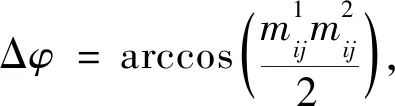
(7)

其中上角标1和2代表两个不同的矩张量.由于将震源时间函数进行了单位化，得到的结果地震矩M0越接近1的说明结果越好，而Δφ则越接近0越好.

3 反演试验结果与分析

3.1 单台六分量与单台平动三分量

首先考虑图3a所示情况，比较用单台平动和单台平动加旋转分别反演得到的结果.图4a和图4b分别展示了两种反演得到的矩张量差异角Δφ分布，可以看到引入旋转的反演结果对应的Δφ更小，说明反演质量得到了显著提升.图4c展示了两种情况下反演得到的地震矩分布结果，引入旋转分量的反演结果在1附近分布更多，标准差更小，说明旋转分量对地震矩起到了很好的约束作用.

图4d显示了采用不同深度的格林函数进行反演得到的归一化残差(式(5))，可以看到平动反演的残差几乎不随深度发生变化，但加入旋转记录后，反演深度与正演深度(10 km)不一致时残差会显著增加，说明旋转对于深度有显著强于平动的分辨能力，这与Donner 等(2016)的结论一致.我们推测其原因是在较低的频段下旋转地震被与深度相关的低阶面波主导，对深度非常敏感，也因此对与深度相关的矩张量元素(Mxz、Myz、Mzz)有更强的约束能力.在附图1中，我们展示了由不同深度的Myz激发的Z分量平动与旋转格林函数波形，并计算了它们与真实震源深度(10 km)下的格林函数波形之间的归一化残差，可见旋转格林函数波形随深度发生的变化较平动更为显著，印证了旋转记录对深度的强分辨能力.

附图1 (a)不同深度下Myz在图3a台站激发的Z分量旋转格林函数波形，波形下的数值为它们与10 km情况的格林函数波形的残差(类似于式(5))；(b)类似于(a)但为平动格林函数；(c)(a)和(b)中的残差随深度变化曲线，红色为旋转分量，蓝色为平动分量Fig.A1 (a)The Z component rotational Green′s functions at station in Fig.3a excited by Myz at different depth,the numbers under the waves are the Misfits (similar to equation (5))between them and the condition in 10 km.(b)Similar to (a)but for translational Green′s functions.(c)Misfits in (a)and (b)at different depth,the red ones denote rotational components while the blue ones denote translational components

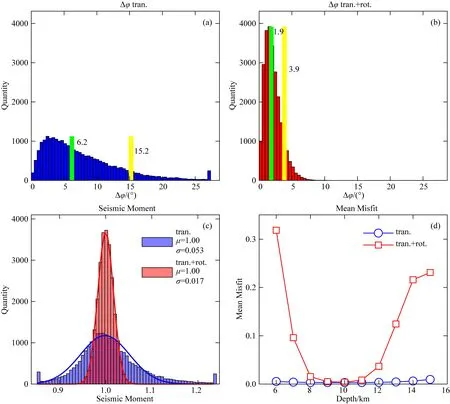
图4 单台平动加旋转和单台平动反演结果比较(a)单台平动反演得到的矩张量差异角Δφ分布，绿色的竖线和黄色的竖线分别代表Δφ中位数处和90%的位置;(b)单台平动加旋转反演结果，图件说明同(a);(c)地震矩(即M0)结果分布，红色和蓝色柱状图分别为单台平动加旋转和单台平动的结果，红色和蓝色曲线为拟合得到的最佳正态分布曲线;(d)用不同深度的格林函数反演得到的波形与原始波形的平均残差，红色和蓝色曲线分别为平动加旋转和平动的结果.Fig.4 Comparison of the inversion results from inversions with translational and rotational components at 1 station and those using only translational components at 1 station(a)The distribution of Δφ obtained by using only translational components.The green bar denotes the medium value of Δφ and the yellow bar denotes the 90% position.(b)The distribution of Δφ obtained by using both translational and rotational components.Please refer to (a)for captions.(c)The distribution of seismic moments (M0).The blue bars and red bars denote results obtained by using both translational and rotational components,and only translational,respectively.The blue and red curves denote respectively the fitting curves of normal distribution for them.(d)The mean Misfits between the original waveforms and the inverted waveforms with Green′s functions at different depths.The red and blue curves denote the results using both translational and rotational components,and only translational components,respectively.

图5展示了两种情况下得到的不同矩张量元素的差异分布，我们发现加入旋转反演后所有矩张量元素结果都得到了改善，其中Myz的改善最为显著.图6给出了各矩张量元素在台站产生的平动与旋转的最大幅度，其中Mzz激发的Z方向旋转振幅为0，图中未画出.可以观察到不同矩张量元素激发出的三分量平动和旋转的振幅都具有非常好的互补性，在反演中它们将联合作用，提高对矩张量元素的约束能力.可以推测，如果在反演中给予平动和旋转不同的权重，结果也将发生变化.若给予旋转较大权重，则旋转约束较好的矩张量元素会更可靠，反之平动约束较好的矩张量元素会更可靠.整体而言，二者权重不宜相差过大，否则其互补作用将不能充分体现，因此本文将平动和旋转的权重设为1∶1.

图5 输入和反演得到的矩张量各元素的差异分布图其中蓝色柱状图为单台平动反演结果，红色柱状图为单台平动加旋转反演结果.蓝色和红色曲线是分别用正态分布进行拟合得到的它们的最佳正态分布曲线.Fig.5 The distribution of difference between the input and inverted moment tensor elementsThe blue bars are for that using only translational components at 1 station,while the red bars are for that using both translational and rotational components at 1 station.The blue and red curves denote respectively the best fitting curves of normal distribution for them.

图6 各矩张量元素在图3a台站处产生的平动和旋转分量的最大振幅的对数值(a)E方向(正东);(b)N方向(正北);(c)Z方向(竖直向上).Fig.6 The logarithmic value of the maximum amplitudes of translational and rotational ground motions produced by different moment tensor elements at the station shown in Fig.3a(a)E component (east);(b)N component (north);(c)Z component (vertical).

3.2 双台平动三分量与单台平动加旋转六分量

本节我们考虑对比两种情况：①在单台三分量平动的基础上增加一个台站的三分量平动；②在单台三分量平动的基础上加入该台站的三分量旋转.在情况①中，原台站位于正北方震中距为1°处，分别尝试在正东方1°处和正南方1°处增加一个台站的三分量平动(图3b和图3c)，反演结果及其比较见图7.

对比图7a—b与图4b—c，虽然在正南方向增加一个平动台站相比单台平动反演有一定改进，但仍不如在原台站处增加旋转分量.然而，当额外增加的平动台站位于正东时(图7c—d)，其结果与单台平动加旋转反演接近.实际上不论是增加旋转还是增加平动，本质上都是提供额外的信息，由于提供的信息不同，提升的作用存在差异.对比图7e和图7f可以看到，在正东增加台站可以较好地改进之前约束最差的Myz，但在正南增加台站提供的信息与原正北台站重复度较高，对Myz的约束依然不好.整体而言，在单台平动反演基础上增加旋转能起到强于额外增加一个平动台站的作用，尤其是对于Δφ较大的矩张量，改进效果更为显著.

图7 (a)、(b)南-北台站(图3b)平动反演结果；(c)、(d)东-北台站(图3c)平动反演结果，图件说明同图4a、c；(e)台站分布为图3b时Myz的误差结果；(f)台站分布为图3c时Myz的误差结果Fig.7 (a)(b)Inversion results obtained with only translational components of 2 stations in the south and the north (Fig.3b),(c)(d)Inversion results obtained with only translational components of 2 stations in the east and the north (Fig.3c),please refer to Fig.4a,c for captions.(e)Error of Myz with the station distribution in Fig.3b.(f)Error of Myz with the station distribution in Fig.3c

3.3 双台六分量、四台平动三分量与四台六分量

针对方位角覆盖更充分的四个台站的情况(图3d)，我们展示和比较了北-东双台平动加旋转分量和东-西-南-北四台平动分量的结果对比(图8)，可以看到二者Δφ和地震矩的分布结果相近，这说明它们提供的约束程度基本相当.另外，四台平动加旋转分量的反演效果相比四台平动反演有显著提升(图9).值得注意的是，格林函数波形归一化残差随深度变化的趋势(图8d、图9d)与3.1和3.2节结果相似：加入旋转都能显著提升对矩心深度的分辨能力.整体而言，在稀疏台站的情况下，在已有台站加入旋转分量能起到不弱于甚至强于增加相同数量的平动分量的作用.

图8 北-东双台平动加旋转分量与四台平动分量(图3d)的反演结果比较，图件说明同图4Fig.8 Comparison of the inversion results obtained with translational and rotational components of 2 stations in the north and the east,and those obtained with only translational components of 4 stations (Fig.3d).Please refer to Fig.4 for captions

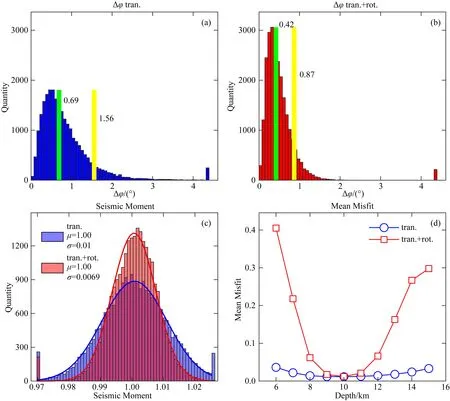
图9 四台平动加旋转分量与四台平动分量(图3d)反演结果比较，图件说明同图4Fig.9 Comparison of the inversion results obtained with translational and rotational components of 4 stations,and those obtained with only translational ground motions of 4 stations (Fig.3d).Please refer to Fig.4 for captions

3.4 16台六分量与32台平动三分量

最后，考虑台站覆盖足够充分的16台平动加旋转分量与32台平动分量(图3e)的情况，反演结果比较见图10，可以看到在原台站处增加旋转比额外增加同样数量的平动台站结果更好，这说明旋转分量提供的空间梯度信息比增加一倍数目的平动分量提供的信息更有效.图11展示了各个矩张量元素误差的情况，可以观察到除Mzz外其他矩张量元素的反演误差都很小，而加入旋转分量对于Mzz结果的改善非常明显.加入旋转分量对Mzz结果的改善可能也与深度相关，旋转被低阶面波主导，因此在矩心深度更准确的同时对Mzz的约束也更加有效.以上结果说明，在平动台站方位角及震中距覆盖充分的情况下，增加平动台站的密度可能效果比较有限，而在原有台站的基础上增加旋转分量，能提供位移所欠缺的空间梯度信息，从而更好地约束矩张量反演结果.

图10 16台平动加旋转分量和32台平动分量(图3e)的反演结果比较，图件说明同图4Fig.10 Comparison of the inversion results obtained with translational and rotational components of 16 stations,and those obtained with only translational components of 32 stations (Fig.3e).Please refer to Fig.4 for captions

图11 16台平动加旋转分量与32台平动分量(图3e)情况下输入和反演得到的各矩张量元素的差异分布图，图件说明同图5Fig.11 The distribution of difference between the input and inverted moment tensors obtained with translational and rotational components of 16 stations,and with only translational components of 32 stations (Fig.3e).Please refer to Fig.5 for captions

4 讨论

前述的反演试验都是在特定条件下进行，比如频段都是0.005～0.02 Hz，添加噪声之后的波形信噪比都为10，接下来对这些可能影响试验结果的因素做进一步的试验和讨论.

4.1 频段的影响

保持其他条件不变，在图3b所示的台站分布下，保持频率下限0.005 Hz不变，尝试不同的频率上限，比较南-北双台平动加旋转分量、正北单台平动加旋转分量和南-北双台平动分量的结果.为了更好的量化比较，我们主要考察Δφ在中位数和90%处的数值，并探究它们随频率的变化.从图12a—b中可以看到，这三种情况得到的反演效果都随频率上限升高而变差，但是双台平动分量和双台平动加旋转分量的结果整体变化幅度相对较小，而单台平动加旋转分量的结果随着频率增加而急剧变差.这可能是使用相对高频的成分进行矩张量反演时，需要更好的方位角覆盖.同时也观察到双台平动加旋转分量的结果普遍略好于双台平动分量，也就是说在相对宽的频段的情况下加入旋转依然可以起到一定的作用，但作用可能相对比较有限.

图12 (a)Δφ中位数(图4中的绿色竖线)随频率上限变化图；(b)Δφ 90%数值(图4中的黄色竖线)随频率上限变化图；(c)频率上限为0.02 Hz时用不同深度的格林函数反演得到的平均反演残差分布；(d)同(c)但频率上限为0.1 Hz图中蓝色、黑色、红色曲线分别为双台平动分量、单台平动加旋转分量、双台平动加旋转分量(图3b)的反演结果.Fig.12 (a)The variation of the medium values (the green bar in Fig.4)of Δφ inverted with different upper cut-off frequencies.(b)The value of Δφ at the 90% positions (the yellow bar in Fig.4)with different upper cut-off frequencies.(c)The mean Misfits of inversions with Green′s functions at different depths when the upper cut-off frequency is 0.02 Hz.(d)Similar to (c)but the upper cut-off frequency is 0.1 HzThe blue,black,red curves denote results obtained by using 3 translational components at 2 stations,translational and rotational compoenents at 1 station,translational and rotational compoenents at 2 stations (Fig.3b),respectively.

此外，可以观察到随着频率的升高，Δφ变化不完全单调，这可能是由于平动和旋转记录对不同频率成分的敏感性不同，且它们受到噪声的影响可能有差异.随着频率的升高，如果新加入进来的频段受噪声影响相对较小，信息更有效，就会对矩张量反演起到改善作用，反之则会引入错误信息甚至掩盖原有频段的正确信息，使反演结果变差.此外，随着频率的升高，旋转对于深度的约束作用逐渐下降(图12c—d)，说明随着频段升高，高频成分增加，原本对深度敏感的低频低阶面波的贡献减小了.

为了探究上述现象产生的原因，我们对合成波形的频谱进行分析.比较两种情况下的频谱：①f1：原始合成波形加噪声并滤波后的频谱；②f0：原始合成波形直接滤波后的频谱.为了更好量化频谱的差异，定义如下的频谱差异Δ(f)：

(8)

其中|f0|代表f0的模的大小，计算不同频段下的Δ(f)可以观察添加噪声对波形频谱的影响.所有24624个矩张量合成波形的平均Δ(f)随频率上限的变化如图13所示，整体而言在频率下限0.005 Hz不变的情况下，频段越宽噪声对频谱的影响越大，且对旋转的影响普遍大于平动，这可能是频率上限升高后加入旋转反演对结果提升不再显著甚至变差的原因.注意到在频率上限较低时(小于0.02 Hz时)，二者基本上重合，也就是在较低的频段下添加噪声对平动和旋转的影响基本相当.为保证旋转记录对矩张量元素更有效地约束作用，可能需要选择相对较低的频带(比如0.005～0.02 Hz)进行反演.

图13 平均Δ(f)(式(8))随频率上限变化的关系图蓝色和红色分别为平动和旋转波形的平均Δ(f).Fig.13 Relationship between mean Δ(f)(equation (8))and the upper frequencyThe blue and red curves denote the mean Δ(f)of translational and rotational components,respectively.

4.2 不同信噪比的讨论

保持其他条件不变，本文测试了不同信噪比的影响.从图14中可以观察到随着信噪比的增加，三种情况的反演效果都会变好，但含旋转的情况随信噪比变化相对较小，这可能是由于对深度敏感的低阶面波在较低的频段(0.005～0.02 Hz)不易受到噪声的影响.我们还注意到，至少在测试的信噪比范围内，双台平动加旋转分量具有绝对优势，单台平动加旋转分量也普遍优于双台平动分量，尤其在低信噪比的情况下.

图14 不同信噪比时的反演结果，图件说明同图12(a)Δφ中位数；(b)Δφ在90%处的数值.Fig.14 Inversion results with different signal-to-noise ratios.Please refer to Fig.12 for captions(a)Medium values of Δφ;(b)Values of Δφ at the 90% position.

4.3 震中距的影响

保持其他条件不变，台站仍位于正南和正北，本文测试了不同震中距的情况，结果如图15所示.可以观察到双台平动加旋转分量仍有绝对优势，而单台平动加旋转分量在部分情况下相比双台平动分量仍有优势.整体而言震中距越小越有优势，可能是由于旋转的近场项衰减较快，在相对近场的情况下旋转的作用更强.

图15 不同震中距时使用不同数据的反演结果，图件说明同图12(a)Δφ中位数；(b)Δφ在90%处的数值.Fig.15 Inversion results with different epicentral distances.Please refer to Fig.12 for captions.(a)Medium values of Δφ;(b)Values of Δφ at the 90% position.

4.4 考虑速度结构模型误差时

保持其他条件不变，改变反演中计算格林函数的速度结构模型(见图2b—c)，比较双台平动加旋转分量和双台平动分量的结果，如图16所示.可以观察到加入旋转的结果受到了非常严重的影响，Δφ分布显著变大，这表明旋转对于速度结构变化非常敏感.这个现象与旋转对深度敏感类似，本质上与格林函数相关，速度结构改变对旋转格林函数的影响远大于平动.有学者在旋转分量的研究中针对一维和三维速度结构也做了讨论(Donner et al.，2020)，发现用三维速度结构反演时加入旋转效果会更好，这和我们的结论在一定程度上是一致的.这也提示我们，未来用实际旋转数据反演矩张量时，应该用尽可能准确的速度结构，否则旋转分量可能会放大模型中的错误信息对结果造成负面影响.但另一方面，由于对地下速度结构非常敏感，旋转记录在地下速度结构的反演工作中也可起到非常重要的作用.

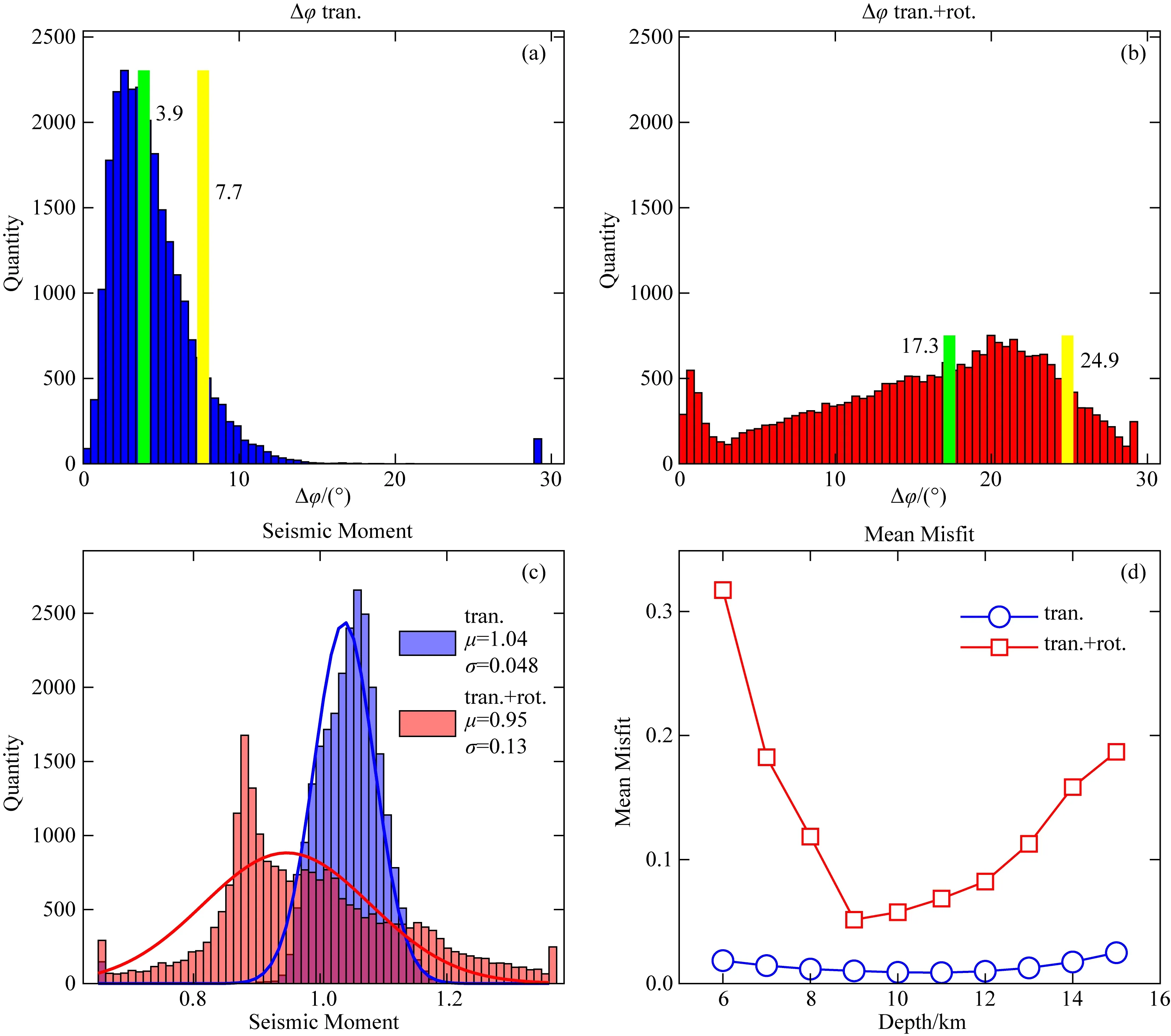
图16 正反演速度结构模型不同时(图2b—c)不同数据反演结果对比，图件说明同图4Fig.16 The comparison of the inversion results when different velocity models are used in forward modeling and inversion (Fig.2b—c).Please refer to Fig.4 for captions

综合上述所有数值试验，在速度模型相对准确且频段合适的情况下，在原有平动台站增加旋转分量具有绝对优势，Δφ普遍减小30%以上；若保持总记录数量不变(即在部分台站增加旋转替代其他台站的平动)，Δφ在90%处的数值普遍比只用平动小，这进一步证实了旋转分量对矩张量元素的约束能力.在平动记录基础上引入旋转分量，有助于得到更准确的矩张量结果.

5 总结与展望

本文从地震动旋转分量的理论公式出发，首先给出了均匀无限空间中位错点源激发的旋转分量和平动分量辐射花样的互补性，从理论上说明加入旋转分量能为矩张量反演提供额外的信息.随后基于层状介质模型的格林函数和复杂震源时间函数，合成得到了平动和旋转的理论地震图.在此基础上开展了多种情况下的矩张量反演试验，对不同的频段范围等试验条件进行了比较讨论，确证了旋转分量可以更好地约束矩张量反演结果，以及旋转分量对矩心深度分辨率更高等结论.

尽管旋转分量的应用可能需要一定的前提，比如较为准确的速度结构和较低的频段，整体而言，将旋转分量应用到矩张量反演中是可行的.比如本文研究发现，在已有台站处增加旋转分量可以更好地约束矩张量反演结果，起到不弱于甚至强于新增平动分量的作用，这适用于台站非常稀疏的情况，比如偏僻的海岛等极端的自然环境下，在同一个台站同时布设平动地震仪和旋转地震仪的成本和难度远小于布设二倍数量的平动台站.另一方面我们也发现，在台站非常密集、方位角覆盖已经比较充分的情况下，在已有台站增加旋转分量比增加同样数量的平动台站更有效，这可为在观测条件较好的地区继续提升地震监测能力提供思路.当然，在实际旋转数据反演中，由于模型和观测的误差非常复杂，与我们开展数值试验得到的认识仍然可能存在一些差异，未来还需要针对实际问题进行更多的分析和讨论.

致谢作者感谢北京大学课程“地球物理研究的论文写作指导”(课程号01201110)对本文语言表述的提升和润色.