利用标准时频变换方法在强噪声环境下无偏拾取地震P波、S波到时
2022-01-25姚彦吉柳林涛盛敏汉许厚泽
姚彦吉,柳林涛,盛敏汉,许厚泽
1 中国科学院精密测量科学与技术创新研究院大地测量与地球动力学国家重点实验室,武汉 430077 2 中国科学院大学地球与行星科学学院,北京 100049
0 引言
地震P波、S波到时的拾取准确率直接影响地震震源位置的反演精度,因此地震P波、S波到时拾取是地震数据处理的一项重要的基础工作(何先龙等,2016;于子叶等,2018).在地震发生后需要快速实现P波、S波到时的精确拾取,这对分析地震发生规律、地震应急、以及后续防震减灾工作尤其关键(张小红等,2012).早期依靠人工拾取地震P波、S波到时,这种方法精度高,但是效率低、主观性强、一致性差(陈金焕等,2015;赵明等,2019).随着地震仪在全球范围的增设以及区域密集台阵的增加,波形数据量急剧增长,收集的数据质量参差不齐,海量数据与强噪声环境的干扰使得震相拾取的精度和速度需求在不断的提高,研究者从时间域、频率域与时频域结合等方面提出了多种波形到时自动拾取的方法(王彩霞等,2013;赵明等,2019).
典型的时间域震相拾取方法有长短时间平均(Short-Term Average and Long-Term Average ratio,STA/LTA)方法(Allen,1978,1982;Baer and Kradolfer,1987).根据波形在振幅、频率等方面的不同特征建立特征方程,使比值灵敏地反映地震信号的到达.但是在信噪比低的场景,应对被噪声干扰的信号时,传统方法往往适应性差且拾取精度难以达到预期(Han et al.,2009).为此,研究者引入多种特征函数(Allen,1978,1982;Baer and kradolfer,1987;Earle and Shearer,1994;高淑芳等,2008;付继华等,2019)增强信号到达时信号幅值等特征的变化,以利于震相的自动准确拾取.AIC(Akaike Information Criteria)方法(Akaike,1974)利用赤池信息准则寻找AIC函数局部最小值作为震相到时,能够抑制强背景噪声的干扰.Maeda(1985)提出了VAR-AIC方法,直接根据地震记录得到AIC函数,AIC函数的局部最小值对应的时间为地震震相到时.为了提高震相的拾取精度,STA/LTA与AIC方法被不断改进(刘劲松等,2013;何先龙等,2016);杨旭等(2019)使用基于参数优化的频带-带宽拾取算法、AICD拾取算法和峰度拾取算法有效拾取地震P、S波到时.另外,神经网络方法也在拾取震相中得到了有效应用(Zhou et al.,2019;赵明等,2019;李健等,2020;Chai et al.,2020).Perol等(2018)应用CNN(Convolutional Neural Networks)对美国俄克拉荷马州地区的连续记录波形进行识别与定位;Zhu和Beroza(2019)使用U-Net识别美国南加州地区P波和S波初至,利用概率分布确定初至波的到时,取得较好的效果.赵明等(2019)基于U形卷积神经网络的震相识别与到时拾取,参照人工拾取结果计算均方根误差Pg为0.41 s,Sg为0.54 s.神经网络方法实现模型有识别信号的能力,需要搭建复杂的网络模型及准备大量已知到时的训练样本.在时间域中拾取地震波到时容易受噪声的干扰,导致到时的拾取存在误差;将地震信号从时间域转换到频率域在一定程度上可抑制噪声的干扰.
不同的地震记录,由于噪声的干扰和介质的复杂性,导致地震信号在时间域、频率域形态上均表现出复杂的特征(Johnston et al.,1979).地震信号往往是一种非平稳信号,其频率的局部化特性对震相、弱震相(刘希强等,1998)的准确拾取十分重要.常用的频率域震相拾取方法有瞬时频率法(Bai and Kennett,2001)、小波变换的主成分分析法(Anant and Dowla,1997;刘希强等,2000)、小波包变换的时频分析法(刘希强等,1998),小波包方法使用小波变换系数刻画信号的突变和渐变,用小波特征进行到时拾取.但是,在强噪声环境中不同的地震记录特征存在较大的差异,单一应用时间域、频率域方法提取的固定特征较难保证所有地震记录的P波、S波到时的精确拾取.
时频分析方法具有较好的抗噪能力,主要包括短时傅里叶变换(Gabor,1946)、小波变换(Grossmann et al.,1985)、S变换(Stockwell et al.,1996)等.Shensa(1977)用快速傅里叶变换的能量谱密度检测震相.刘代志等(2005)采用小波包分解检测地震波信号初至点.Anant和Dowla(1997)、Mousavi等(2016)通过小波变换系数中的偏振和振幅信息拾取P波和S波到时.Pinnegar和Mansinha(2003)、张小红等(2012)根据S变换后时频图上振幅能量的突变来判断P波的到时.S变换具有较好的时频分辨率,相比时域方法具有较强的抗噪能力(王彩霞等,2013).但是,定义在L2(R)空间中的小波变换存在频率偏移现象(Liu and Hsu,2012;苏晓庆,2014),S变换中存在高频部分频率分辨率不准确(武国宁等,2011)的问题,会导致震相到时的拾取产生偏差.柳林涛和许厚泽(2009)提出的标准时频变换方法(Normal Time-Frequency Transform,NTFT),是傅里叶变换、小波变换与S变换的继承与发展.NTFT改进了小波变换、S变换的问题,能无偏地表示信号的即时频率、即时振幅和即时相位,最大限度的保留原始信息,具有较好的时频分辨率(柳林涛等,2016).
考虑震相拾取时间域方法振幅响应灵敏特性与NTFT变换无偏特性的优点,本文提出强噪声环境下地震P波、S波到时拾取的时频域综合方法.通过理论分析、合成测试以及实际数据分析,证实了本文所提出方法的有效性.
1 方法原理
1.1 标准时频变换
NTFT时频分析方法(柳林涛和许厚泽,2009;柳林涛等,2016)满足量纲守恒,信号的频率、振幅和相位随时间的变化而变化,消除了可能存在的伪频率和频率偏移,提高时频谱的分辨率.对于一个时间信号f(t)∈C,其标准时频变换可以表达为:
(1)



(2)
式中,w(t)表示窗函数.在标准时频变换中,核函数的傅里叶变换式(3)满足条件(4),
(3)

(4)
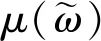
(5)
式中w(t)表示高斯窗,σ表示高斯窗窗宽参数.本文构造的核函数如式(6)所示:
(6)
构建的标准小波变换表达为:

(7)
对一个调和信号(8)式h(t)进行标准时频变换时,可满足(9)式的即时无偏特性.
h(t)=Aexp(j(βt+φ)),
(8)
式中,A表示振幅,β表示频率,φ表示初始相位;βt+φ表示即时相位.

(9)

令t-τ=x,则t=x+τ,
(10)

(11)
所以Ψh(τ,β)=Aexp(j(φ+βτ))=h(τ),一个调和信号的标准时频谱无偏的描述原始信号的特征.
标准时频变换是小波变换与S变换的继承与发展.如图1所示,将一个波形进行不同的时频分析对比,图1a中红点对应时刻的信号成分分别进行小波变换、S变换与NTFT后与图1b,1c,1d中黄色虚线时刻对应.文中小波变换采用的小波基函数为莫雷特小波,小波变换与S变换均需要先验信息调试参数达到最佳分辨率,时频谱中均存在右偏现象,且高频部分时频分辨率较低.标准时频变换无需先验信息,从数据本身出发且保证较高的时频分辨率.从图中波形最大振幅时刻进行判断,在莫雷特连续小波变换中存在0.05 s延迟,S变换中存在0.1 s延迟,标准时频变换能够无偏地描述原始信号的即时特性.标准时频变换的无偏性减少了NTFT方法拾取到时中不必要的偏差,为准确拾取到时提供了有利的基础条件.
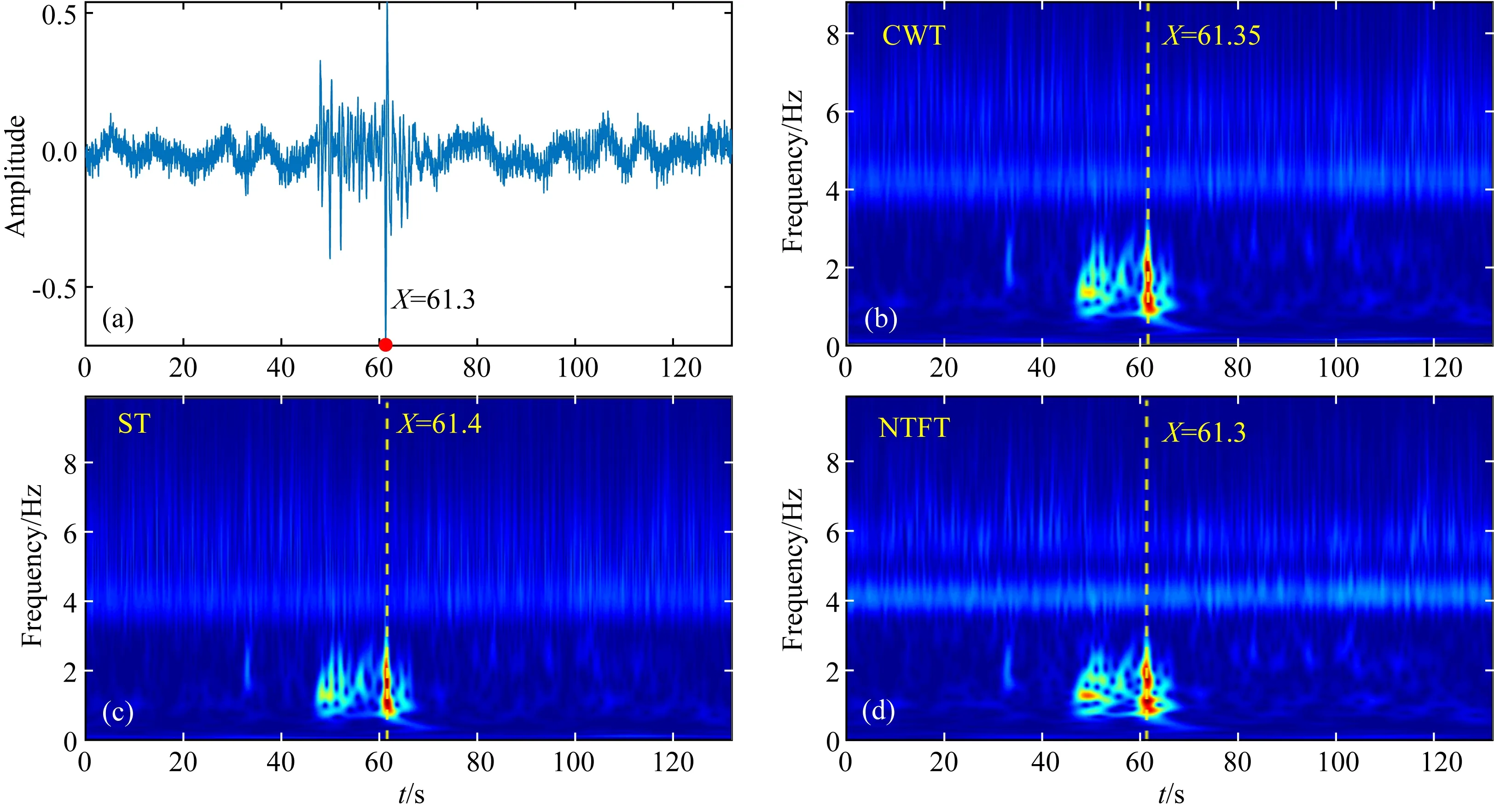
图1 地震信号及其时频谱分析对比(a)地震信号;(b)莫雷特连续小波变换;(c)S变换;(d)标准时频变换.图(a)中红色点为地震信号振幅最大的时刻,时频谱中黄色虚线为地震信号红点变换后对应的时刻.Fig.1 Comparison of seismic signal with its time-frequency spectrum analysis(a)Seismic signal;(b)Morlet continuous wavelet transform;(c)S transform;(d)Normal time-frequency transform.In figure (a),the red dot is the moment when the seismic signal amplitude is the largest,and the yellow dotted line in the spectrum is the moment when the seismic signal is transformed and corresponds to the red dot.
1.2 基于NTFT的STA/LTA方法
NTFT变换可确定地震信号的即时信息,结合NTFT时频谱特征对STA/LTA方法的特征函数进行改进,通过NTFT确定的即时频率对地震信号发生频段进行约束,选取地震信号发生的即时频段[ωp,ωq]进行震相拾取,即时频段的判别过程参见(姚彦吉等,2020),频段约束定义如下:
(12)
(13)

(14)
因此,文中改进特征函数表示为
(15)

(16)
式中,STAi为短窗口的特征函数均值,LTAi为长窗口的特征函数均值,CF为特征函数,S为短窗口宽度,L为长窗口宽度.
公式(15)特征函数能同时响应地震信号即时振幅和即时频率的变化,通过NTFT即时频率对特征函数的频率范围进行约束,可增强地震信号即时振幅和即时频率的变化特征.将(15)式代入(16)式中,分别在长、短窗内计算地震信号特征函数的均值,并通过STA/LTA的值检测P波和S波的到时.
1.3 基于NTFT的AIC方法
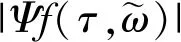
(17)

(18)
或者表示为:
(19)
同理,根据标准时频谱判断信号发生的时间段,设置滑窗的时间范围.
AIC函数定义为(刘劲松等,2013):
AIC(k)=(k-m+1)log{var(G([m,k]))}
+(n-k-1)log{var(G([k+1,n]))},
(20)
G([m,k])(k=m,m+1,…,n)表示被时间段[m,n]与NTFT即时频率段[ωp,ωq]约束的地震信号;var(G[m,k])和var(G[k+1,n])分别表示滑窗内数据集合G[m,k]与G[k+1,n]的方差.
2 算例分析
2.1 合成波形测试
为了测试在强噪声环境下本文方法的性能,我们利用了合成波形检验方法的有效性.利用frequency-wavenumber方法(Zhu and Rivera,2002),根据CRUST1.0模型(Laske et al.,2013),合成了2019年2月23日四川荣县M4.7地震在EMS台的理论波形,信号采样频率为20 Hz.该地震的震源参数根据Yang等(2020)的反演结果得到.用f(t)代表一个理论波形,将f(t)与噪声信号n(t)叠加,如式(21),构成叠加信号s(t)以模拟含有噪声的实际观测地震信号.合成实验中强噪声信号n(t)主要假设为对地震波形到时干扰较大的白噪声、脉冲干扰以及强能量单频噪声三种;脉冲干扰会使地震记录失真,严重影响数据处理结果的质量(周宝峰,2012);叠加的强能量单频噪声为实测地震记录中截取获得,强能量单频噪声在时间域与地震波形相似甚至淹没地震信号(张晟瑞等,2018).
s(t)=f(t)+n(t).
(21)
另外,通过改变噪声信号的功率pn,来研究三种不同背景噪声下地震震相自动拾取方法的实际性能.式(22)为所求叠加信号的SNR.
(22)
式中,ps为信号f(t)的功率,pn为噪声n(t)的功率.
理论地震波形P波到时TP为32.10 s,S波到时TS为47.16 s.分别在白噪声(0 dB)、脉冲干扰(2.5 dB)、强能量单频噪声(-6 dB)三种不同的背景噪声下,采用STA/LTA方法、AIC方法与本文方法对叠加信号s(t)进行地震震相自动提取,并根据拾取结果分析不同背景噪声下各方法的实际性能.STA/LTA的短窗宽度S设为1 s,长窗宽度L设为10 s,P波和S波到时自动拾取的阈值设为2.5.为了更好地与STA/LTA方法比较,基于NTFT的STA/LTA方法也选择同样的长、短窗宽度.
在上述给定的条件下,不同类型的噪声信号n(t)(白噪声0 dB,脉冲2.5 dB)分别随机产生20组,强能量单频噪声(-6 dB)从实测地震数据中截取20组分别与合成地震信号叠加,地震P波和S波自动拾取结果如表1所示.表中误拾率是指地震P波和S波到时拾取误差大于0.1 s的事件所占比例;漏拾率指未拾取到地震P波或S波到时的事件所占比例.
不同背景噪声下地震P波、S波拾取效果如表1所示,在0 dB的白噪声环境下,STA/LTA方法P波出现了20%的误拾率与10%的漏拾率,正确率为70%.VAR-AIC方法P波出现了5%的误拾率,对于S波的拾取,VAR-AIC方法的误差小于STA/LTA方法;基于NTFT的STA/LTA、AIC方法在白噪声干扰的情况下能较好地自动提取地震P波、S波到时,基于NTFT的STA/LTA方法P波拾取结果平均偏差和标准偏差均为0.02 s,S波拾取结果平均偏差和标准偏差均为0.01 s,优于STA/LTA方法与VAR-AIC方法;由于部分合成波形P波初至较弱且被强噪声干扰,导致P波拾取误差偏大.在脉冲干扰(2.5 dB)的环境下,STA/LTA方法受脉冲信号干扰失效,脉冲信号所发生的时刻直接影响STA/LTA计算峰值出现的时刻;对于VAR-AIC方法而言,脉冲信号对到时拾取干扰严重,P波和S波的拾取误差均大于0.1 s.而基于NTFT的STA/LTA的方法能有效拾取P波(平均偏差0.02 s,标准偏差0.02 s)、S波(平均偏差0.02 s,标准偏差0.03 s),基于NTFT的AIC方法明显改善了S波(平均偏差0.01 s,标准偏差0.01 s)拾取结果的偏差.在-6 dB的强能量单频噪声环境下,STA/LTA方法P波误拾率为65%;VAR-AIC方法P波误拾率为35%,S波漏拾率为10%.相比之下,在强噪声干扰的复杂环境中,基于NTFT的STA/LTA方法与基于NTFT的AIC方法仍保持着较高的拾取准确率.

表1 不同背景噪声下地震震相自动拾取统计表Table 1 Automatic picking results of seismic phase under the different background noise
图2为在0 dB强噪声环境下地震信号及其以上四种不同方法的提取结果,图中红色实线表示地震信号P波的理论到时,红色虚线表示S波的理论到时.STA/LTA方法如图2e所示,求得的STA/LTA值在地震P波到时处并无显著优势,背景噪声干扰导致在P波到达时发生漏拾,在P波到达之后S波到达之前误拾噪声信号;基于NTFT的STA/LTA方法如图2f所示,继承了STA/LTA方法的灵敏性,同时噪声得到了较好地抑制,振幅的响应变化明显增强.VAR-AIC方法拾取震相如图2g所示,该方法在强噪声情况下拾取震相具有一定的鲁棒性,但是在P波初至较弱且被强噪声淹没的情况下,P波到时处的AIC函数值变化较弱,导致P波到时拾取存在误差;在相同的背景噪声下,S波到时处AIC函数值变化特征明显,相比P波而言,S波到时的拾取误差较小.基于NTFT的AIC方法拾取震相如图2h所示,除去了地震信号所在频段外的噪声干扰,震相到达时刻的AIC函数值变化特征显著,有利于震相到时的准确拾取.
图3为脉冲干扰环境下一组地震信号及其以上四种不同方法的拾取结果.脉冲信号对震相拾取的准确率影响较大,脉冲干扰产生的原因有记录器故障、周围环境的突发性变化和干扰、以及操作人员的过失等(周宝峰,2012).如图3c为STA/LTA方法计算结果,脉冲信号发生的位置引起了较大的振幅响应变化,很难从阈值的角度加以剔除,容易导致地震信号震相拾取发生错误.脉冲信号也使得VAR-AIC方法有较高的误拾率与漏拾率,如图3e所示,AIC计算的局部最小值并非地震信号的到时.脉冲信号相对于地震信号分布于高频段,在STA/LTA方法与AIC方法中引入NTFT可选取地震信号所在频段拾取到时,有效抑制脉冲对地震信号的干扰.
进一步测试本文方法在不同强噪声干扰下的稳定性能,我们分别从实测数据中截取强能量单频噪声与理论地震信号叠加进行测试.单频噪声产生的原因有仪器噪声、高压线或人为活动、以及机器运行等,在时间域中极易干扰甚至淹没地震信号(张晟瑞等,2018).如图4所示,在时间域中地震信号的P波初至完全被强噪声掩盖,在STA/LTA方法中如图4c漏拾P波到时;VAR-AIC方法如图4e在P波到时处也无显著优势.在噪声淹没的情况下,NTFT-STA/LTA方法如图4d所示能较好的拾取P波与S波到时,但是在面波结束之后,与地震信号处于同一频段的噪声容易发生误拾取情况,NTFT-STA/LTA方法的拾取精度受阈值影响;相对于NTFT-AIC方法而言,如图4f所示P波与S波到时特征明显,地震信号P波与S波的到时拾取不依赖于阈值的选取.

图4 强能量单频噪声干扰(-6 dB)下理论地震信号到时自动拾取结果(a)叠加强能量单频噪声的地震信号及其标准时频谱(b);(c)STA/LTA方法的拾取结果;(d)NTFT-STA/LTA方法的拾取结果;(e)VAR-AIC方法的拾取结果;(f)NTFT-AIC方法的拾取结果.Fig.4 Automatic picking of theoretical seismic phase under high energy single frequency noise interference (-6 dB)(a)Seismic signals superimposed with high energy single frequency noise and their Normal Time-Frequency spectrum (b);(c)Picking result of STA/LTA method;(d)Picking result of NTFT based STA/LTA method;(e)Picking result of VAR-AIC method;(f)Picking result of NTFT based AIC method.
在不同环境噪声下我们对四种方法进行了对比分析,STA/LTA方法、VAR-AIC方法与NTFT结合使波形在分界点出现明显的突变,提高了拾取结果的精度.在STA/LTA的计算结果中,振幅、频率突变的响应结果中包含较多的毛刺干扰,导致拾取到时时较难把控阈值的选择.阈值过低容易引发误拾,阈值过高则又导致漏拾,说明STA/LTA较难拾取强噪声背景环境下的震相到时.基于NTFT的STA/LTA方法计算结果较为光滑,信号振幅响应优势明显,利于到时的自动拾取.相比VAR-AIC方法,基于NTFT的AIC方法具有较好的稳定性与鲁棒性,在不同噪声干扰下均保持较高的拾取准确率.
2.2 实测数据拾取结果对比
为了进一步检验本文方法对于实际地震P波和S波到时拾取的可靠性,将基于NTFT的STA/LTA方法与基于NTFT的AIC方法应用于实测地震数据,我们选用了105条信噪比较低的波形(图5),均为汶川余震记录的垂直分量.数据来自“余震捕捉AI大赛”提供的汶川地震余震信号(Fang et al.,2017).应用四种方法对105条余震信号进行到时拾取,并将四种算法拾取的结果与人工拾取的结果进行了比较.实测数据为多个台站的不同事件,波形记录中P波与S波到时受到了强噪声的干扰,甚至到时信息被噪声淹没,波形特征如图5所示.105条波形P波的平均信噪比为2.9 dB,S波为2.5 dB.为了方便比较分析,实验中STA/LTA方法与NTFT-STA/LTA方法计算短窗口宽度S均设为1 s,长窗口宽度L均设为10 s,地震P波和S波到时拾取阈值均设为3.

图5 105条余震记录的波形特征Fig.5 The waveform characteristics of 105 aftershock records


图6 实测地震信号的到时拾取(a)滑窗范围选定过程;(b)滑窗直接从标准时频谱中选取信号;(c)不同滑窗拾取的到时;(d)滑窗拾取的最佳到时与VAR-AIC方法拾取结果对比;(e)STA/LTA方法与NTFT-STA/LTA方法拾取结果对比.图中红色实线表示信号的P波到时,红色虚线表示信号的S波到时,绿色的虚线表示面波结束时刻.|A|表示对信号的振幅取模.Fig.6 Picking-up arrival time of the measured seismic signal(a)The selection process of sliding window areas;(b)The sliding window selects the signal directly from the Normal Time-Frequency spectrum;(c)Arrival times of seismic phases picked up by different sliding windows;(d)The optimal pickup results of sliding window and VAR-AIC method;(e)Results picked up by STA/LTA method and NTFT-STA/LTA method.In the figure,the solid red line represents the P-wave arrival time,the dotted red line represents the S-wave arrival time,and the dotted green line represents the end of the surface wave.|A|means the modulo operation of the amplitude of the signal.
基于本文提出的方法对105组实测地震数据进行了P波、S波到时的拾取,实验中的余震记录均按照人工拾取的P波到时为30 s统一截取.文中四种方法均对原始地震记录直接进行到时拾取,前30组余震记录到时拾取结果对比如表2所示.根据表2可知,噪声的干扰导致STA/LTA方法漏拾次数较多,且S波到时的漏拾次数远远大于P波,S波到时的漏拾率为9.52%,P波为0.95%.通过NTFT对STA/LTA特征函数的改进,S波漏拾率降为1.90%,P波则没有漏拾.VAR-AIC方法在低信噪比地震信号到时拾取中存在一定的漏拾,P波漏拾率为0.95%,S波漏拾率为1.90%;将VAR-AIC与NTFT结合对低信噪比地震信号拾取到时,P、S波到时漏拾情况得到较好的改进.可见STA/LTA与AIC方法中引入NTFT有效抑制了地震信号频段外的强噪声干扰.

表2 前30组地震记录P波和S波自动拾取结果(单位:s)Table 2 Automatic picking results of P and S waves in 30 groups of seismic records (unit:s)
为了检验本文方法的有效性,我们将相同的30组余震记录通过Vaezi和Van Der Baan(2015)的PSD(Power Spectral Density)方法进行到时拾取,参照人工拾取结果统计误差,将NTFT-STA/LTA方法、NTFT-AIC方法与PSD方法的P波、S波到时拾取误差进行了比较如图7所示,其中在PSD方法中有11组数据发生P波或S波到时漏拾的情况.30组数据为不同台站的多个事件,在背景噪声复杂多样的情况下,PSD方法对P波初至不敏感拾取误差较大,相比之下,NTFT-STA/LTA方法与NTFT-AIC方法对P波、S波到时的拾取精度较高.

图7 三种方法到时拾取误差比较(a)P波到时拾取的误差比较;(b)S波到时拾取的误差比较.Fig.7 Error comparison of arrival time pickup of three methods(a)Error comparison of P-wave pickup;(b)Error comparison of S-wave pickup.
另外,我们应用了STA/LTA方法、NTFT-STA/LTA方法、AIC方法与NTFT-AIC方法对105条余震记录拾取震相到时,其中11条余震记录包含P波或S波发生漏拾取的情况,其余的余震记录拾取结果对比分析如图8所示.将四种方法拾取的到时结果与人工拾取结果对比分析,NTFT的引入较好的改善了震相到时的拾取精度;背景噪声复杂多变,STA/LTA方法与AIC方法拾取精度受噪声影响较大,NTFT分别引入两种方法后,拾取精度均得到了较好的改善,但相比于NTFT-STA/LTA方法而言NTFT-AIC方法拾取精度更为稳定.

图8 四种方法到时拾取结果(a)P波到时拾取的结果;(b)S波到时拾取的结果.Fig.8 Picking results of the arrival times with four methods(a)Picking results of P-wave arrival times;(b)Picking results of S-wave arrival times.
如表3所示,我们计算并统计了105组实测地震记录到时拾取结果的误差.表3中误拾次数是指地震P波和S波到时拾取误差大于1 s的事件次数;漏拾次数指未拾取到地震P波或S波到时的事件次数.STA/LTA方法到时拾取精度依赖于阈值的选取,在强噪声干扰的环境下,STA/LTA方法因强噪声干扰导致较高的误拾率或漏拾率.相比于STA/LTA方法,AIC方法拾取准确率较高,但在强噪声淹没地震信号时,AIC计算窗口的划分具有不确定性,NTFT的引入可直观设置AIC计算窗口初始参数.在给定相同参数下,NTFT的引入不需要通过阈值反复权衡误拾率和漏拾率便可以获得较为理想的地震P波或S波到时.基于NTFT改进的STA/LTA方法P波拾取结果的均方根误差为0.36 s,S波拾取结果的均方根误差为0.56 s;相对容易遗漏较难拾取的S波,NTFT引入后S波的漏拾率降低了1/5;NTFT-AIC方法优于NTFT-STA/LTA方法,P波拾取结果的均方根误差为0.25 s,S波拾取结果的均方根误差为0.35 s.四种方法拾取P波与S波的误差离散分布情况如图9所示,相比S波的拾取,P波拾取误差相对较小.NTFT的引入使STA/LTA方法与AIC方法到时拾取准确率均有提高,并较好的改善了P波、S波漏拾的情况,这是本文方法具有比较大实用性的地方,充分发挥了NTFT的无偏性与STA/LTA、VAR-AIC方法的灵敏性.

图9 四种方法拾取结果的误差离散分布情况统计图中“+”表示拾取误差较大的异常值.Fig.9 The error discrete distribution statistics of seismic phase pickup results by four methodsThe “+”in the figure means the outlier with a large pickup error.
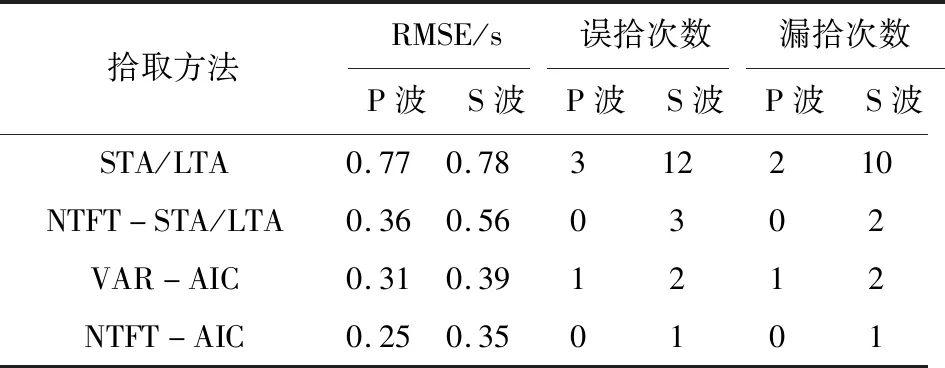
表3 对105组地震记录P波和S波拾取结果的误差统计Table 3 Error statistics of P and S wave pickup results of 105 groups of seismic records
3 讨论
地震信号复杂多样,实现地震信号P波、S波到时准确、稳定、快速拾取难度较大.本文研究显示,将NTFT引入STA/LTA与AIC方法中,还存在两个主要的问题:
(1)地震信号到时的拾取仍存在误差.P波与S波到时较相近时,S波受P波尾波与噪声的干扰导致到时拾取误差偏大,S波相对于P波较难拾取.
(2)当噪声与地震信号分布于同一频段、同一时间段时,极易混淆模糊震相,导致震相到时误拾或漏拾的情况.
如图10所示,图中竖实线表示人工拾取的地震P波的到时,竖虚线表示人工拾取的地震S波的到时.在P波与S波到时相隔较近且受强噪声干扰的情况下,STA/LTA方法与AIC方法均较难准确拾取S波.在STA/LTA方法中,引入NTFT后,如图10c中所示,S波虽能被拾取,但是与人工拾取的结果存在较大的误差.如图10d中所示,VAR-AIC方法与NTFT-AIC方法对S波到时拾取失效.对这些信噪比低,P波震相与S波震相相隔较近的地震事件,自动精确拾取到时还存在一定的困难.我们将NTFT与CNN结合(姚彦吉等,2020),应用NTFT+CNN算法识别地震信号,并提高震相到时拾取精度;还可以联合多台站技术(Zhang and Wen,2015)与本文所提出的方法来识别并提取震相到时.

图10 震相漏拾情况分析(a)实测地震记录;(b)与(a)对应的地震信号的标准时频谱;(c)STA/LTA方法与NTFT-STA/LTA方法拾取结果与人工拾取结果对比;(d)VAR-AIC方法、NTFT-AIC方法拾取结果与人工拾取结果对比.图中红色和蓝色的竖直实线表示人工拾取的P波到时,红色和蓝色的竖直虚线表示人工拾取的S波到时.Fig.10 Analysis of seismic phase leakage pickup(a)The measured seismic record;(b)The Normal Time Frequency spectrum of the seismic signal corresponding to (a);(c)Comparing the results picked up by the STA/LTA method and NTFT-STA/LTA method with the manual results;(d)Comparing the results picked up by the VAR-AIC method and NTFT-AIC method with the manual results.In the figure,the red and blue vertical solid lines represent the P-wave arrival time picked by manual,while the red and blue vertical dotted lines represent the S-wave arrival time picked by manual.
4 结论
随着地震台站的不断增设,地震数据急剧增多,强噪声的干扰给海量地震数据的处理带来了挑战,针对地震P波和S波到时自动、快速、准确拾取的问题,本文在STA/LTA、AIC方法的基础上,引入了NTFT,结合信号时间域与频率域特征,提出了基于NTFT的STA/LTA方法,以及基于NTFT的AIC方法.
通过理论分析,合成数据及实测数据测试,基于NTFT的地震P波与S波自动拾取方法继承了STA/LTA、AIC方法振幅响应敏感的优点,同时还具有以下特征:
(1)基于NTFT的STA/LTA方法,建立了NTFT与特征函数的内在联系,该方法能较好的压制地震信号频段外噪声对震相拾取的干扰.STA/LTA方法在强噪声环境下,其拾取结果的误拾率与漏拾率显著增大,基于NTFT的STA/LTA方法计算确定地震信号所在的即时频段,通过提取出地震信号所在的频段有效拾取震相到时.
(2)基于NTFT的AIC方法,能够适应多种噪声的复杂环境,具有一定的稳定性,并且地震P波、S波到时拾取误差均较小,NTFT的引入进一步增强了AIC方法的鲁棒性.基于NTFT的AIC方法,结合了AIC方法的准确性与NTFT方法的无偏特性,提高了震相自动拾取的准确率.
(3)NTFT对STA/LTA与AIC方法的改进,均增强了振幅响应变化特征,响应处振幅较大且两边较光滑,毛刺较少,减少了对到时拾取的干扰.
致谢感谢中国地震局地球物理研究所赵明副研究员提供整理的波形震相数据集.
