初始扰动对静力适应过程的影响
2022-01-25郭海龙王宁刘宇迪崔新东
郭海龙,王宁,刘宇迪*,崔新东
1 国防科技大学气象海洋学院,长沙 410000 2 北京应用大气研究所,北京 100029
0 引言
地转平衡和静力平衡是大气中最基本的两种诊断关系,各种性质的强迫作用使得平衡遭到破坏,同时大气又通过波动的频散作用不断地重建平衡,从而实现大气物理量场之间的调整适应.
对于地转适应过程的研究,从Rossby(1938)、Monin和Obukhov(1959)等开始,一直到巢纪平(1962a,b)等的完善,详细地说明了大气中风场与气压梯度场之间的相互调整过程,从而解决了风成因的这一科学问题;而对于静力适应过程中涉及的垂直气压梯度场和浮力场之间的相互调整过程,研究尚不明确.
从Lamb(1932)问题开始,Bannon(1995,1996)、Sotack和Bannon(1998)、Almgren(2000)、Chagnon和Bannon(2001)、Duffy(2003)、van Delden(2015)、崔新东等(2016)、郭海龙和刘宇迪(2018a,2018b)等的研究证实,声重力波的频散作用是实现垂直气压梯度场和浮力场相互调整的物理机制,并给出了调整过程中能量的基本转换情形,在这种绝对理想的假设下,解决了空气块受初始温度扰动后垂直气压梯度场和浮力场之间相互调整的原理问题,Duffy(1997,2003)、Chagnon和Bannon(2005a,2005b)、Fanelli和Bannon(2005)、Edson和Bannon(2008)利用非静力数值模式,研究了在持续的热力学强迫和动量强迫下,静力适应过程中的波动响应情况和能量转换情况,但未能揭示此过程中垂直气压梯度场和浮力场的因果关系,在实际可压缩性较强的大气中,垂直气压梯度场和浮力场之间的相互作用和制约是大气运动过程中重要的环节,清楚地解释垂直气压梯度场和浮力场之间的因果关系,以及影响这种因果关系的因子,有助于更加深刻地理解大气运动过程的本质.
基于此,本文从非静态线性模型出发,在均匀介质的波动理论假设下,探讨初始扰动性质对于静力适应过程的影响,试图去揭示在静力平衡被不同性质的扰动破坏后,垂直气压梯度场和浮力场、垂直气压梯度场和水平流场u分量之间的因果关系,并从能量转换的角度,描绘在不同性质扰动后,大气运动的物理本质.
本文的结构安排如下:第二部分给出非静态、可压缩、等温大气静力适应过程的数学模型,从理论上描述初始扰动在静力适应过程中扮演的角色;第三部分讨论在不同初始扰动下垂直气压梯度场和浮力场、垂直气压梯度场和水平流场u分量之间的适应关系,研究初始扰动对静力适应过程的影响;第四部分研究在不同初始扰动下,静力适应过程中的扰动能量分配情况和扰动能量之间的转换情况,揭示不同初始扰动下,大气运动的物理本质;第五部分为结论部分.
1 数学模型
数学模型采用在局地直角坐标系中描述完全可压缩等温干大气的原始方程组,忽略运动方程中的科氏力作用项、摩擦力作用和黏性作用,略去由地球旋转引起的惯性波和Rossby波,假定大气运动过程绝热,并满足理想气体状态方程,利用小扰动法,将物理量写为平均量和扰动量之和的形式,在热力学变量的扰动分量远远小于其基态分量,且热力学基态分量在水平方向分布均匀的条件下,保留水平基流垂直切变的影响,将原始方程线性化得到
(1a)
(1b)
(1c)
(1d)
(1e)
(1f)
其中D/Dt≡∂/∂t+u0(z)∂/∂x,γ≡cp/cv≈1.4称为Poisson指数,带上标的量为扰动变量,带下标的量为基态变量,基态变量满足静力平衡和状态方程:
(2)
引入变量代换:
(u*,v*,w*,p*,ρ*,θ*)=
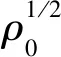
(3)
假设扰动量满足简谐波运动规律且振幅仅随时间发生变化,解的形式可写为
f*=Re(FA(t)ei(kxx+kyy+kzz)),
(4)

(5)
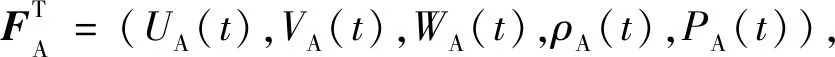


(6)
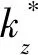
(λ+iku0)[(λ+iku0)4+a(λ+iku0)2+b(λ+iku0)+d]=0,
(7)
其中对应系数分别为
(8)
由式(6)求得矩阵A的特征值对应的特征向量矩阵为
(9)


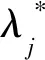
(10)
式(10)中的系数Cj由初始条件决定:
(11)
其中上标“-1”表示矩阵的求逆运算,由式(11)可知,初始扰动的性质决定式(10)中的系数,表征着声重力波各分支在适应过程中对扰动变量的贡献权重.将式(11)代入式(10)中有
×E-1×FA(0),
(12)
其中需满足特征向量矩阵为非奇异矩阵,由式(12)可知,静力适应过程是由五支波动对初始扰动频散的过程,若初始扰动为零,则物理量随时间不发生变化;而不同的初始扰动则对应不同的频散结果.再将式(12)代入式(5)可得到,在静力适应过程中,各物理量随时间的演变方程为
×E-1×FA(0),
(13)
则在静力适应过程中各物理量场随时间的相对变化为
(14)
其中参量μρp,用来判断在适应过程中浮力场与垂直气压梯度场的相对变化大小,若μρp远大于1,表示垂直气压梯度场变化远小于浮力场的变化,则是浮力场向垂直气压梯度场适应,相反,则为垂直气压梯度场向浮力场适应.由式(1a)得到
(15)
其中参量μup用来判断在适应过程中水平流场u分量与垂直气压梯度场的相对变化大小,若远大于1,表示垂直气压梯度场变化远小于水平流场u分量的变化,则有水平流场u分量适应垂直气压梯度场;相反,则有垂直气压梯度场适应水平流场u分量.
2 初始扰动与适应方向的关系
基于式(12),将初始扰动分为热力学扰动和动力学扰动,取垂直波数为kz=2π/Hs,水平波数kx=ky,取垂直水平比δ分别为0.1、1、10来表征中、小、微三种特征尺度的扰动系统,取基本气流分布模型为西风急流型,表示为
u0(z)=umax+U(z-Hs)2,
(16)
其中(umax,U)为常数,定义水平基流向东为正,其中z为垂直高度,本文中选取范围为0≤z≤2Hs,Hs=RTs/g为大气标高,Ts表示地表温度,等温大气中基态量随垂直高度的变化有如下关系:
(17)
其中κ=R/cp,当取最大水平风速umax=30(m·s-1),基本气流和大气基本参数垂直分布如图1所示.
图1显示,按垂直高度将目标大气分为三层,0~6 km表征对流层低层,6~10 km表征对流层高层,10~16 km表征平流层低层,水平基流随着垂直高度先增加后减小,急流轴位于对流层高层,基本态的气压和密度随高度呈指数递减,而位温则随高度呈指数递增.
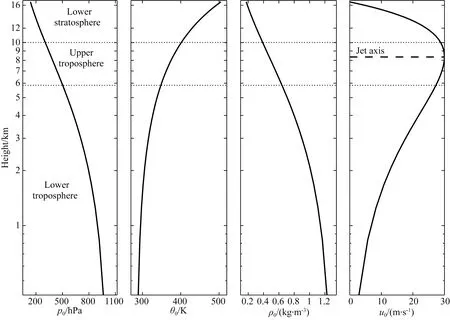
图1 基本气流及大气参数分布Fig.1 The distribution of basic flow and parameters of atmospheric
2.1 初始扰动为单位水平速度
当初始扰动仅为单位水平速度时,有FA(0)T=(1,0,0,0,0),在xz平面内,取空间平均后的垂直气压梯度场、浮力场和水平流场u分量随时间的相对变化情形如图2所示.
图2显示,当δ=0.1时,在对流层低层(图2g),在受扰后的二十几分钟内,有μρp<1,表示浮力场的变化小于垂直气压梯度场的变化,则垂直气压梯度场向浮力场适应;二十几分钟以后,有μρp>1,表示浮力场的变化大于垂直气压梯度场的变化,则浮力场向垂直气压梯度场适应;当时间继续增加时,垂直气压梯度场和浮力场的变化呈振荡型逐渐趋于一致;而水平速度场的变化,除在个别时刻外,基本小于垂直气压梯度场的变化,有垂直气压梯度场向水平流场u分量适应的特征.在对流层高层(图2d),参量μρp先随时间增加,在二十几分钟后达到峰值,随后在五十几分钟时取最小值,说明受扰后,先由垂直气压梯度场向浮力场适应,逐渐变为浮力场适应垂直气压梯度场,紧接着又变回垂直气压梯度场适应浮力场,而参量μup则始终小于1,表示在整个过程中垂直气压梯度场向水平速度场适应;在平流层低层(图2a),物理量之间的相对变化情形同图2g相似.当δ=1时,在平流层低层(图2d)和对流层高层(图2e),垂直气压梯度场和浮力场之间相互适应,水平流场u分量和垂直气压梯度场同步变化;而在对流层低层(图2h),受扰后的三十几分钟内,垂直气压梯度场和浮力场相互适应,随后,有参量μρp>1,μup>1,则浮力场和水平流场u分量均向垂直气压梯度场适应.当δ=10时,在整层大气中(图2c、2f、2i),有μup>1,则水平流场u分量向垂直气压梯度场适应,而浮力场和垂直气压梯度场相互适应.

图2 水平速度扰动下μρp(黑色)和μup(灰色)的分布Fig.2 The distribution of μρp (black line)and μup (gray line)for the horizontal velocity perturbation
2.2 初始扰动为单位垂直速度
设初始扰动仅为单位垂直速度,则有FA(0)T=(0,0,1,0,0),在xz平面内,取空间平均后的垂直气压梯度场、浮力场和水平流场u分量随时间的相对变化情形如图3所示.
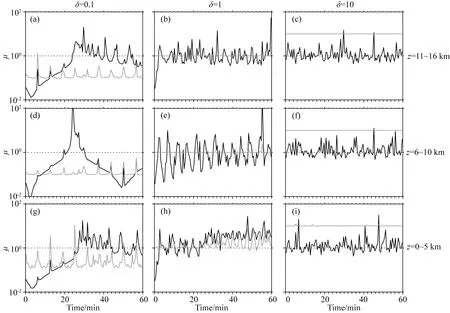
图3 垂直速度扰动下μρp(黑色)和μup(灰色)的分布Fig.3 The distribution of μρp (black line)and μup (gray line)for the vertical velocity perturbation
比较图2和图3可知,浮力场、垂直气压梯度场和水平流场u分量之间的相互适应关系,在这两种扰动条件下,基本保持一致;这说明,在固定的扰动尺度、垂直高度和基本气流等条件下,当初始扰动均为动力性时,静力适应过程中物理量的变化规律相同.
2.3 初始扰动为单位密度
设初始扰动仅为单位密度,则有FA(0)T=(0,0,0,1,0),在xz平面内,取空间平均后的垂直气压梯度场、浮力场和水平流场u分量随时间的相对变化情形如图4所示.
图4显示,当δ=0.1时,参量μρp的分布特征同图2和图3中相似,而μup在扰动后的前两分钟内远远大于1,表示垂直气压梯度场向水平速度场快速适应,随后μup迅速减小,扰动场由水平流场u分量向垂直气压梯度场适应.当δ=1时,在平流层低层(图4b),μρp围绕着μρp=1呈振荡型分布,表示垂直气压梯度场和浮力场相互适应;在对流层高层(图4e),μρp呈振荡型增长,振幅随时间减小,在前二十几分钟内,垂直气压梯度场和浮力场相互适应,而在后期则由浮力场向垂直气压梯度场适应;在这两层中,扰动后的两分钟内,垂直气压梯度场向水平速度场快速适应,随后,垂直气压梯度场和水平速度场同步变化;在对流层低层(图4h),扰动后的几分钟内,μρp从小于1迅速增大,而μup在大于1的范围内呈振荡型变化,表明在适应过程中浮力场逐渐向垂直气压梯度场适应,水平流场u分量向垂直气压梯度场适应.当δ=10时,在各层中μρp和μup均远大于1,表明,浮力场和水平流场u分量的变化远大于垂直气压梯度场的变化,即浮力场和水平流场u分量均向着垂直气压梯度场适应.

图4 密度扰动下μρp(黑色)和μup(灰色)的分布Fig.4 The distribution of μρp (black line)and μup (gray line)for the density perturbation
2.4 初始扰动为单位气压
设初始扰动仅为单位气压,则有FA(0)T=(0,0,0,0,1),在xz平面内,取空间平均后的垂直气压梯度场、浮力场和水平流场u分量随时间的相对变化情形如图5所示.
图5显示,当δ=0.1时,在平流层低层(图5a)和对流层低层(图5g),扰动后的20 min内,有μρp>1,且呈减小趋势,表明浮力场的变化大于垂直气压梯度场的变化,由浮力场向垂直气压梯度场适应;随后在28 min和42 min左右,各出现一个峰值,在平流层低层,后期主要是垂直气压梯度场向浮力场适应,而对流层低层后期为垂直气压梯度场和浮力场之间的相互适应,水平流场u分量在扰动后迅速向垂直气压梯度场适应,而后便是垂直气压梯度场向水平流场u分量适应;在对流层高层(图5d),μρp呈两峰夹一槽的分布特征,在受扰初期,浮力场向垂直气压梯度场适应,中期转为垂直气压梯度场向浮力场适应,后期又回归为浮力场向垂直气压梯度场适应的特征,而在整个过程中垂直气压梯度场则向水平流场u分量适应.当δ=1时,在平流层低层(图5b)和对流层低层(图5h)中,μρp的分布特征随时间呈反相关,前者随时间振荡减小,起初为浮力场向垂直气压梯度场适应,渐变为相互适应,水平流场u分量和垂直气压梯度场呈同步变化,而后者则随时间振荡增加,浮力场的变化逐渐大于垂直气压梯度场的变化,水平流场u分量的变化逐渐增大,大于垂直气压梯度场的变化;在对流层高层(图5e),μρp呈振荡型分布,振幅逐渐减小,而μup的分布近似为μup=1的直线.当δ=10时,在平流层低层(图5c)和对流层低层(图5i)中,随时间减小趋向于1,表明在微尺度扰动中,浮力场变化大于垂直气压梯度场变化,而则呈准直线分布均大于1,表明水平流场u分量向垂直气压梯度场适应;在对流层高层(图5f),μρp沿μρp=1的直线呈振荡型分布,即垂直气压梯度场和浮力场相互适应,而μup依旧呈大于1的直线分布,有水平流场u分量向垂直气压梯度场适应.
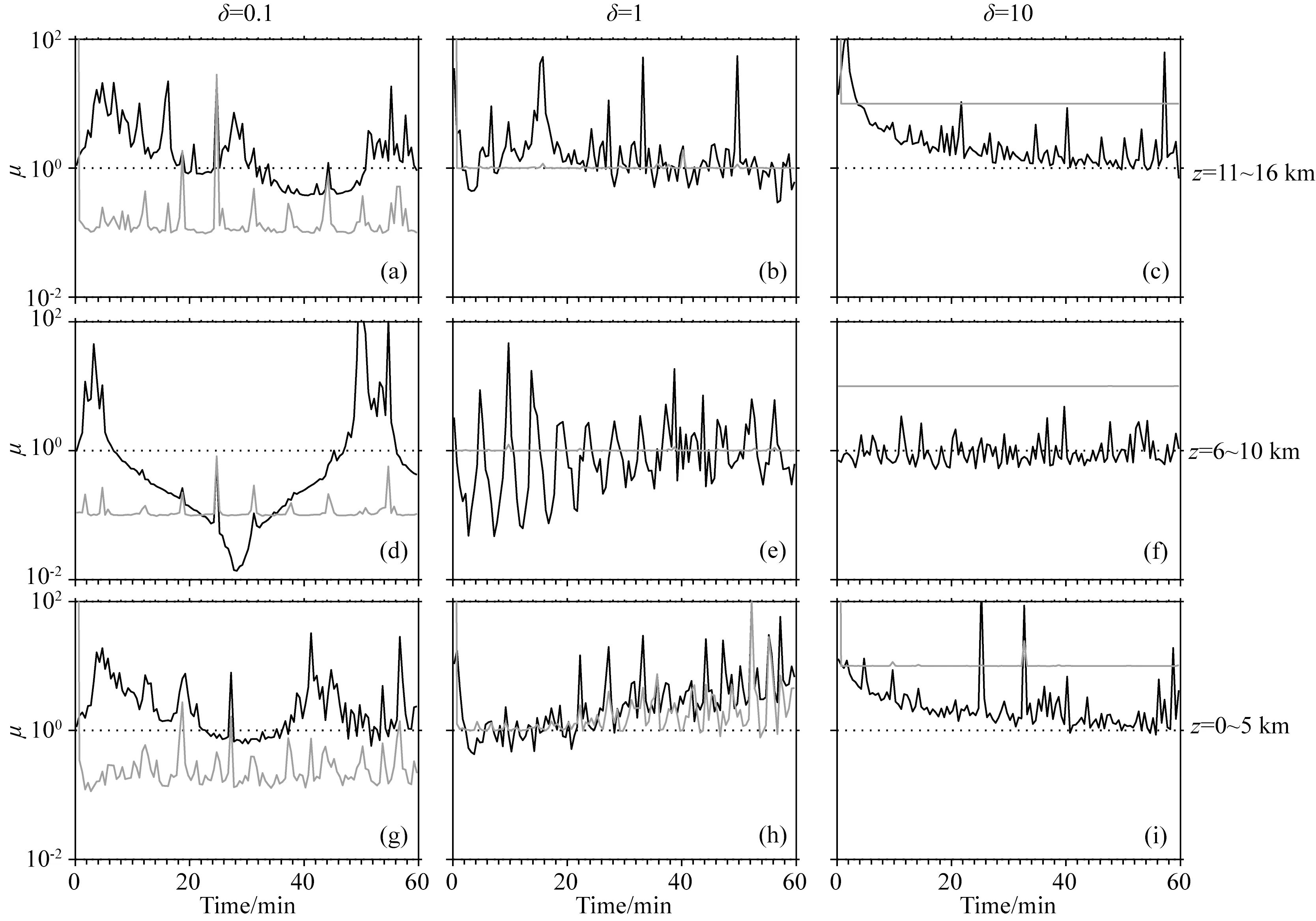
图5 气压扰动下μρp(黑色)和μup(灰色)的分布Fig.5 The distribution of μρp (black line)and μup (gray line)for the pressure perturbation
3 初始扰动与能量转换的关系
静力适应过程中扰动总能量由扰动动能,扰动有效势能,扰动弹性势能组成,其表达式分别为
Eall=Ekh+Ekv+Eae+Eap
(18)
将式(10)代入式(18)可得到
(19)
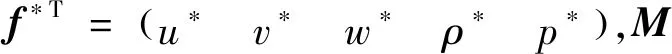
(20)
进一步可将式(20)写为
ψ=Re(Ediag(eλjt)E-1ei(kxx+kyy+kzz))
j=1,2,3,4,5
(21)
其中diag(eλjt)表示以eλjt为元素的对角矩阵,λj为特征向量,E为特征向量矩阵,i为虚数单位,Re为取实部运算.由式(21)可知,扰动总能量与初始扰动、波动螺旋结构、基本气流及其垂直切变等要素相关.
进一步,将式(18)和式(21)代入方程式(1),可得到各种扰动能量之间的转换关系为
(22a)
(22b)
(22c)
其Cae→kh为扰动水平动能与扰动弹性势能之间的转换,Cae→kh>0,表示弹性势能向水平动能转换,即气压梯度力作用下的水平运动;Cae→kv为扰动垂直动能与扰动弹性势能之间的转换,Cae→kv>0,表示弹性势能向垂直动能转换,即静力平衡破坏后的垂直运动;Cae→ap为扰动有效势能与扰动弹性势能之间的转换,Cae→ap>0,表示弹性势能向有效势能转换,即浮力作用下的垂直运动;由式(22)可知,当大气完成静力适应过程时,此项为零,取垂直水平比等于0.1,则在不同性质的扰动下,适应过程中能量的分配和转换讨论如下.
3.1 初始扰动为水平动能
当初始扰动为单位质量的水平动能时,设FA(0)T=(1,0,0,0,0),在xz平面内,取空间平均后的扰动能量分配和扰动能量转换情况随时间的变化如图6所示.
图6a、6c、6e显示,当空气块受到水平动能扰动后,在整个适应过程中,扰动能量主要以Ekh的形式存在,其次为Eae,且随着垂直高度的增加,Eae在总扰动能量中的比例增加,而Ekv和Eap的比例接近于零.图6b、6d、6f显示,在适应过程中,|Cae→kh|和|Cae→kv|的转换占据主要地位,而|Cae→ap|的转换则相对较小,表征大气中主要的动力过程为气压梯度力作用下的水平运动和静力平衡被破坏后的垂直运动,在二十分钟左右|Cae→kv|的转换远大于其他能量之间的转换,表示静力平衡破坏后引起的垂直运动最为显著.
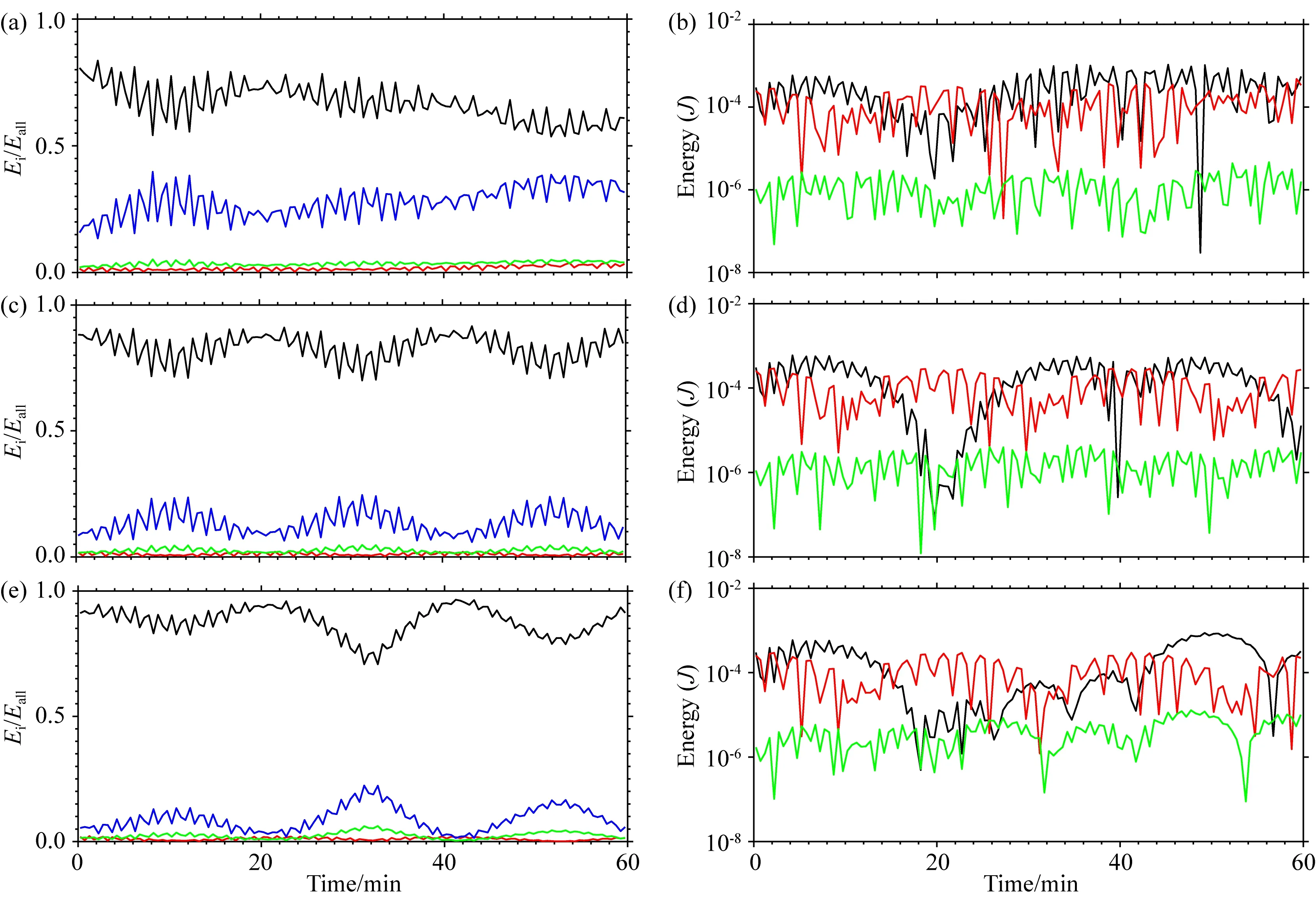
图6 水平动能扰动后能量的分配及转换(a)表示Ekh(黑色)、Ekv(红色)、Eap(绿色)和Eae(蓝色)与Eall的比值;(b)表示|Cae→kh|(黑色)、|Cae→kv|(红色)和|Cae→ap|(绿色)的转换情况,(a、b)表示平流层上层,(c、d)表示对流层上层,(e、f)表示对流层低层.Fig.6 The partition and conversion of energy for the horizontal kinetic energy perturbation(a)Graphs show the ratio of Ekh (black line),Ekv (red line),Eap (green line),and Eae (blue line)to the Eall,respectively;(b)Graphs show the conversion of |Cae→kh| (black line),|Cae→kv| (red line),|Cae→ap| (green line),respectively.
3.2 初始扰动为垂直动能
当初始扰动为单位质量的垂直动能时,设FA(0)T=(0,0,1,0,0),在xz平面内,取空间平均后的扰动能量分配和扰动能量转换情况随时间的变化如图7所示.
图7a、7c、7e显示,当空气块受到初始垂直动能扰动后,在对流层高层和平流层低层中,扰动能量主要以Eae和Ekv的形式存在,且Eae>Ekv>Eap≫Ekh,随着垂直高度的降低,扰动能量中Ekv的比例增加,Eae的比例减小,在对流层低层,有Eae≈Ekv,随着时间的增加,Ekv的比例增加.由图7b、7d、7f可知,在整个适应过程中,|Cae→kv|的转换远大于其他能量形式之间的转换,即在垂直动能扰动下,静力平衡破坏后的垂直运动为大气运动的主要形式,随着时间的增加,在平流层下层中,能量之间的转换成增加趋势,即表征扰动的发展,而在对流层高层,能量之间的转换区域稳定,在对流层低层,能量之间的转换随时间减小,表征扰动的衰减.
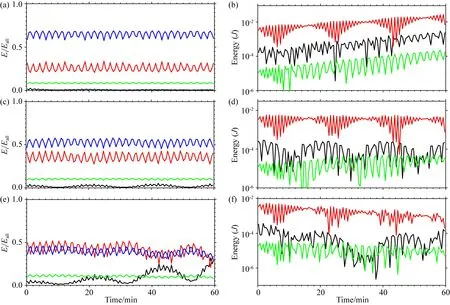
图7 垂直动能扰动后能量的分配及转换(图中标识同图6)Fig.7 The partition and conversion of energy for the vertical kinetic energy perturbation (the identifications are the same as Fig.6)
3.3 初始扰动为有效势能
当初始扰动为有效势能时,设FA(0)T=(0,0,0,1,0),由线性化后的扰动状态方程可知,初始时刻只有扰动有效势能,在xz平面内,取空间平均后的扰动能量分配和扰动能量转换情况随时间的变化如图8所示.
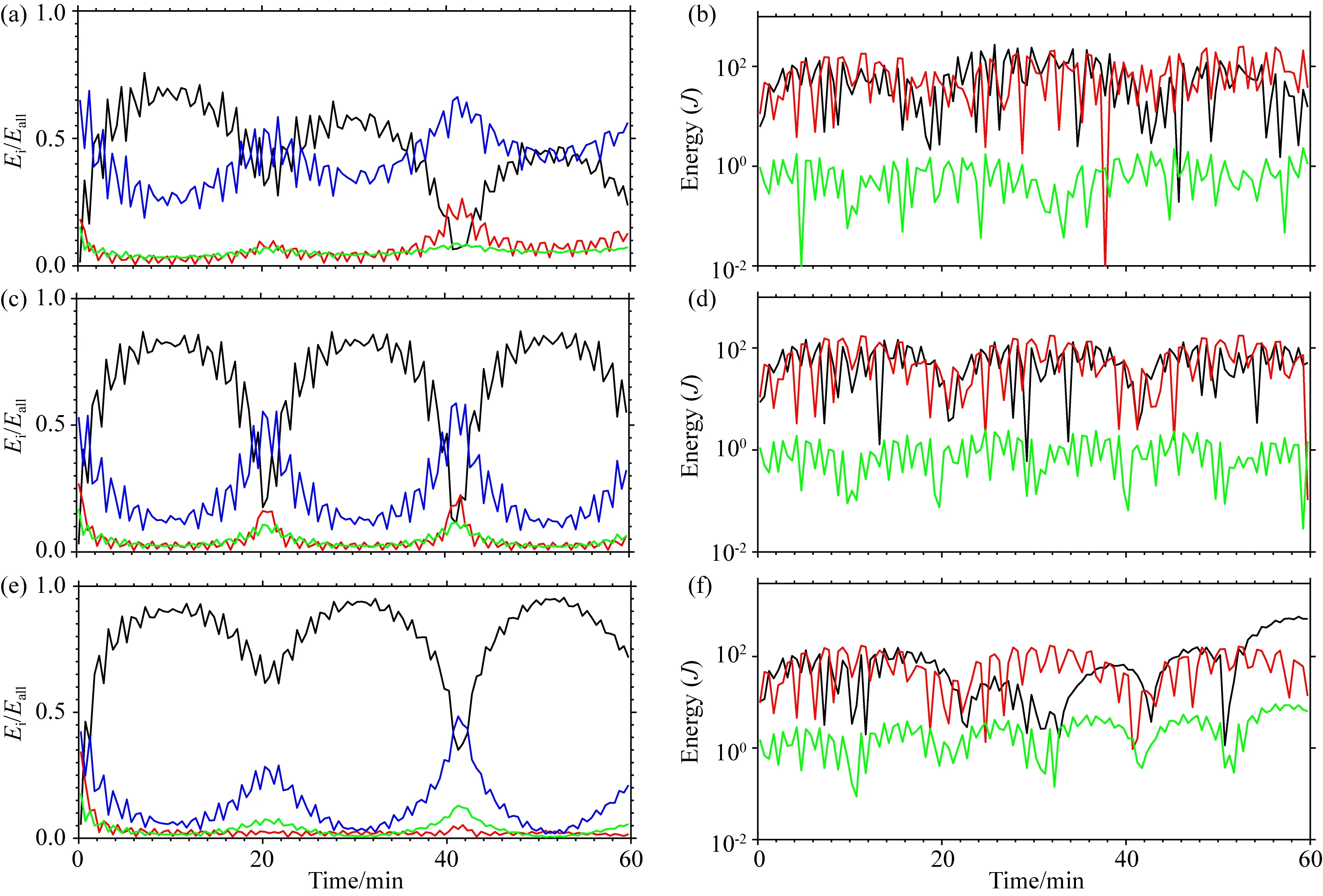
图8 有效势能扰动后能量的分配及转换(图中标识同图6)Fig.8 The partition and conversion of energy for the available potential energy perturbation (the identifications are the same as Fig.6)
由图8a、8c、8e可知,初始时刻的扰动有效势能立刻转化为弹性势能和水平动能,在整个适应过程中,扰动能量主要以Ekh和Eae的形式存在,且随时间呈反位相的波动状分布,随着垂直高度的降低,Ekh呈增加趋势,而Eae呈减小趋势;其余两种形式的能量同Eae保持同相位分布,有Eae>Ekv≈Eap.图8b、8d、8f显示,在适应过程中,|Cae→kv|和|Cae→kh|的转换呈同量级,均远大于转换项|Cae→ap|,即表明此时大气中主要的动力过程为气压梯度力作用下的水平运动和静力适应破坏后引起的垂直运动,而在垂直方向的热量通量输送则较不显著.在对流层低层,随着时间的增加,垂直方向的热量通量输送效应增加,气压梯度力作用下的水平运动也呈增加趋势.
3.4 初始扰动为有效弹性势能
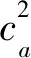
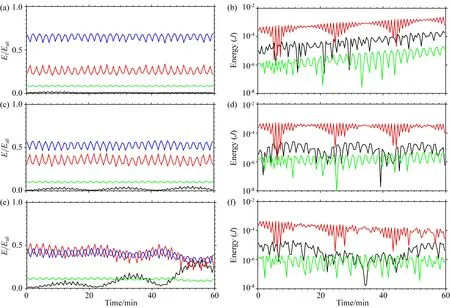
图9 有效弹性势能扰动后能量的分配及转换(图中标识同图6)Fig.9 The partition and conversion of energy for the available elastic energy perturbation (the identifications are the same as Fig.6)
比较图7和图9可知,当气块受到有效弹性势能的扰动后,此时各扰动能量形式所占的比例同气块受到垂直动能扰动后的情形一致,且各能量之间的转换情形也相似,仅存在转换量级的差异.这也说明,气块受到垂直动能和有效弹性势能的扰动后,大气静力适应过程中的动力学过程是相同的,其中垂直动能的作用增强垂直热量通量的输送效应.
4 结论
本文为了研究初始扰动性质对大气静力适应过程的影响,从描述非静态、可压缩、等温干大气静力适应过程的线性模型出发,利用均匀介质中的波动假设,分类研究了四种初始扰动下垂直气压梯度场和浮力场、垂直气压梯度场和水平流场u分量之间的适应关系;并从能量分配和能量转换的角度揭示了不同扰源下大气静力适应过程的物理本质.
当大气静力适应过程被破坏后,垂直气压梯度场和浮力场之间不再平衡,大气通过声重力波的作用,使得相互作用、相互制约的垂直气压梯度场和密度场重新分配,从而重新建立新的平衡,在此过程中,垂直气压梯度场和密度场、垂直气压梯度场和水平流场u分量之间相互适应的因果关系受波动螺旋结构、水平基流及初始扰动性质等因素的影响,其中,初始扰动性质决定了声重力波各分支在静力适应过程中的贡献大小,从而影响着各物理量场随时间的分布.
在水平基流为西风急流模型假设下,初始的速度扰动和密度扰动对中尺度系统中垂直气压梯度场和浮力场的相互适应过程具有相似的作用,在静力平衡被破坏的前20 min内,均有浮力场的变化小于垂直气压梯度场的变化,表明垂直气压梯度场向着浮力场适应,而在20 min以后,随着垂直高度的差异,这种适应关系有显著的区别,当初始扰动为气压扰动时,在平衡破坏后的前期和后期均有浮力场的变化大于垂直气压梯度场的变化,表明浮力场向垂直气压梯度场适应,而在中期,适应方向相反.在小尺度系统中,初始扰动性质对于静力适应过程影响的差异较小,在对流层低层,平衡破坏后的初期垂直气压梯度场和浮力场同步变化,随着时间的增加,逐渐演变为浮力场向垂直气压梯度场适应.在微尺度系统中,初始速度扰动引起的物理量场之间的适应关系基本相同,而在初始密度扰动下,在整层大气的适应过程中,均有浮力场的变化远大于垂直气压梯度场的变化,表明浮力场向着实际垂直气压梯度场适应;在初始气压扰动下,在对流层低层和平流层低层,平衡破坏初期有浮力场向垂直气压梯度场适应,逐渐演变为浮力场和垂直气压梯度场之间的相互适应.
对于静力适应过程中水平流场u分量与垂直气压梯度场之间的适应关系,初始扰动性质对其影响不显著,而扰动尺度对其的影响却十分明显,在中尺度系统中,有水平流场u分量的变化远小于垂直气压梯度场的变化,即垂直气压梯度场向水平流场u分量适应,在小尺度系统中,水平流场u分量和垂直气压梯度场的变化量级相当,有垂直气压梯度场和水平流场u分量相互适应,在微尺度系统中,垂直气压梯度场的变化远小于水平流场u分量的变化,有水平流场u分量向垂直气压梯度场适应;这也表明,当静力平衡被破坏后,在微尺度系统中,垂直气压梯度场是大气运动的因,而在中尺度系统中,水平流场u分量是大气运动的因.
初始扰动的性质影响适应过程中扰动能量的分配比例和扰动能量之间的转换情况,不同性质的初始扰动,引起大气运动的物理本质不同.当大气静力平衡被水平动能扰动或有效势能扰动破坏后,在适应过程中,扰动能量主要以扰动水平动能和扰动弹性势能的形式存在,而扰动能量之间的转换以扰动弹性势能、扰动垂直动能和扰动水平动能之间的转换为主,此时大气运动的物理本质主要为气压梯度力作用下的水平运动和静力平衡被破坏后引起的垂直运动为主.而当初始扰动为垂直动能或有效弹性势能时,扰动能量主要以弹性势能和垂直动能的形式存在,所占比例随着垂直高度变化而变化,扰动能量主要在弹性势能和垂直动能之间转换,此情形中静力平衡破坏后引起的垂直运动占据绝对主导.
对于初始扰动性质对静力适应过程影响的研究,本文仅从单一的扰动因子出发做了探讨,而实际大气中,破坏静力适应过程的扰动是动力学和热力学因素的综合,要准确地揭示扰源性质对静力适应过程的影响,确定垂直气压梯度场和浮力场之间的因果关系,需要综合考虑各种影响因子,这还有很长一段路要走.
