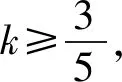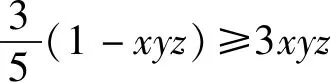2021年塞浦路斯奥赛不等式试题的推广

福建省福清第一中学 (350300) 李云杰

试题呈现设x,y,z>0且满足x2+y2+z2=3，求证xyz(x+y+z)+2021≥2024xyz①.

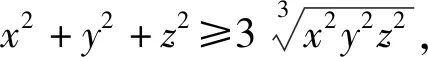
张老师的证明构思巧妙，充分利用了题设条件和各数量之间的关系.沿用上述证明过程，可证在原题设条件下，当k≥1时，有xyz(x+y+z)+k≥(3+k)xyz.当k<1时，上述证法失效，不等式xyz(x+y+z)+k≥(3+k)xyz还能否成立？经探究，本文得到更一般的结论.